2. 哈尔滨工业大学 数学系, 150001 哈尔滨
2. Dept. of Mathematics, Harbin Institute of Technology, 150001 Harbin, China
随着通信卫星在军事、商业以及人民的日常生活中越来越广泛的应用,对通信卫星的综合效能评估就显得越来越重要了.针对不同的目的,通信卫星的效能评估方法一般有WSEIAC方法、层次分析法、灰色模糊分析方法、神经网络方法等[1-13].这些方法各有其优缺点和适用范围,例如WSEIAC方法的优点是在能够给出模型需要的可用度向量、可信赖矩阵、能力矩阵的情况下,能够对系统做出精确的效能评估,它的缺点是需要大量且准确的统计数据做为基础,推算出模型需要的可用度、可信度和系统能力;层次分析法能够使定性与定量相结合,并且应用广泛,但是相较其他几种效能评估方法,计算量较大;模糊分析法能够对定性的判断进行量化,计算过程也十分简洁,但它分析的力度比较粗,得到的评估结果不够精确;神经网络方法是具有自主学习与调整能力的效能评估方法且不会出现局部最优解,但其模型的建立颇为复杂,人为提供的训练集的优劣直接影响着模型的效率.
本文的目的是从整体上对通信卫星的综合效能进行评估和把握,特别要考虑当整体效能提高之后,其稳定性的减弱以及造价的上涨所带来的影响.鉴于评估的指标包含许多综合指标,并且所包含的性能无法统一度量,因此本文将借助模糊数学中的一些理论和方法来构建评价模型,类似的思想,还可见于文献[14].由于专家对各指标的评价等级基本一致,所以本文侧重点在模糊隶属函数的构建上,且关键在于隶属函数的选取,相对于传统的隶属函数,本文的隶属函数更符合这类评价对象的性质且具有更好的光滑性.
1 基于模糊理论的评价模型给定一个评价对象,先对其进行数学上的抽象,设其为X,对它的评价有m个指标,记为x1, …, xm,其中xi又与n个指标相关,记为xi=(xi1, …, xin),i=1, …, m,通过规范化,不妨设0≤xij≤1,1≤i≤m,1≤j≤n.因此,X可以看作一个m×n阶矩阵, X ={xij}m×n.取论域为
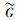
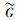
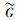

|
(1) |
其次,由于当每个指标(因素)提高到一定程度之后,评价对象的稳定性将会随之减弱,并且其造价也会上涨,所以关于每个指标,都存在一个临界值,当其小于这个临界值时,随着指标的提高,其整体评价水平会大幅度提高,因此对这一对象的评价是加速上升的,而当其大于这个临界值时,虽然整体评价水平会继续提高,但由于上述负面因素的影响,本文的评价应当是减速上升的.这一现象反映到所要构造的隶属函数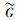
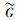
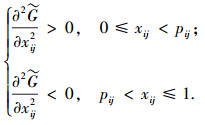
|
(2) |
并且由于任意两个指标是相互独立的,因此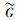
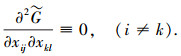
|
(3) |
综上所述,本文最终的目标是寻找一个满足式(1)~(3)的评价函数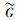
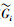
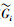
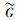
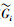
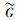
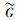
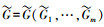
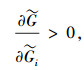
|
(4) |
由上述构造可知
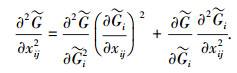
|
很显然,这样的
1) 固定1≤i≤m,定义满足条件式(1),(2)的函数
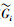
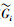
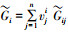
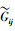
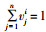
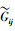
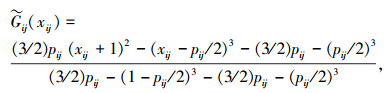
|
显然这样定义的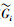
2) 确定
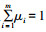
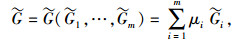
|
则这样定义的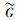
设X1, …, Xk是k个同类型的评价对象且Xα={xijα}m×n,1≤α≤k,接下来对其进行分类.
定义1 定义两个评价对象Xα, Xβ的综合相关指数为rαβ=1- 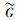
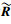
注意到0≤rαβ≤1,且rαβ越接近1,Xα, Xβ的相关性越强,rαβ越接近0,Xα, Xβ的相关性越弱.
定理1 取论域为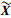
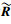
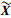
证明 首先,显然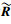
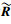

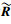

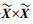
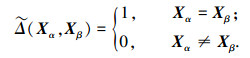
|
即
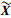
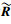
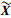
设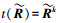
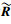
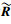
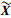
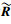
在本文中,应用模糊理论提出的评价模型,来建立东方红系列卫星平台通信卫星的效能评估模型.
其指标体系中的特征指标通常包括转发器功率、转发器质量、工作寿命、发射质量、整星输出功率、平台质量、载干比、频率覆盖范围等.
首先,对这一指标体系做数学上的抽象.注意到这些指标有的是定量指标,有的是定性指标,本文首先要做的是将这些指标量化并且将其量纲一的统一.简便起见,将每一因素的最大值设为1.令x1, …, x7分别表示转发器功率、转发器质量、工作寿命、发射质量、整星输出功率、平台质量和载干比,即此模型中的m=7,n=1.由模糊理论评价模型的讨论,可定义
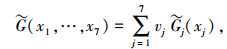
|
其中vj>0,j=1, …, 7是满足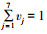

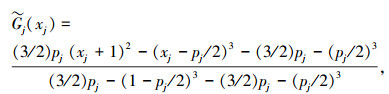
|
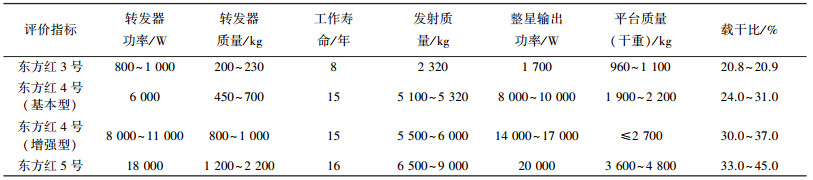
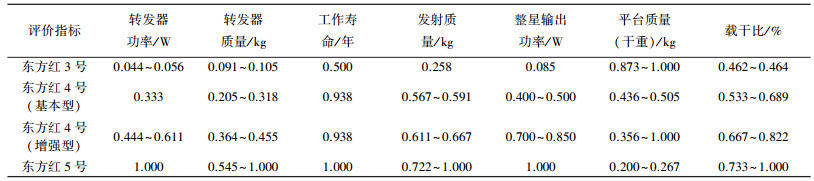
这里0<pj<1,j=1, …, 7是常数,确定为每个因素现阶段的平均水平.本文基于表 1中东方红系列卫星平台通信卫星各指标的主要参数来构造评价函数进行评价为例.首先,由于各指标的单位、评价标准各不相同,为了进行综合评估,将其进行统一处理,使它们在表 1数据中的最优值为1,评估最低值为0(保留小数点后3位),见表 2.
| 表 1 东方红系列卫星平台通信卫星指标参数 |
| 表 2 归一化处理后的东方红系列卫星平台通信卫星指标参数 |
根据数据,取p1=0.387,p2=0.352,p3=0.863,p4=0.594,p5=0.561,p6=0.580,p7=0.659,则对每个指标,本文可以得到评价函数
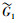
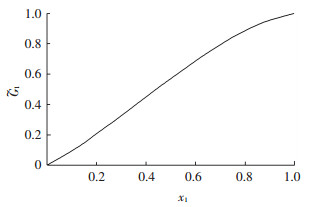
|
图 1
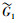 |
从其图像来看,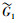
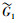
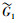
| 表 3 东方红系列通信卫星各指标的评价 |
选取一组权重(权重的选取可依据专家打分方式获得),例如,取
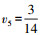
| 表 4 东方红系列通信卫星的综合评价 |
这样,本文就从定量的角度对东方红系列卫星平台通信卫星进行了综合的评估.从评估结果来看,东方红系列通信卫星的整体效能是一直呈上升趋势的,但综合来看,东方红5号的整体效能并没有比东方红4号增强型高出太多.
从上述讨论可以看出,相比于其他的评估模型,本模型的计算比较简洁.注意到本文中所构造的是一个S型隶属函数,在传统方法中,S型模糊隶属函数通常构造为由两个二次函数构成的分段连续但不光滑函数(见文献[15]).与传统方法相比,本文的隶属函数不但连续,并且是光滑的,因此更符合评估中“循序渐进”的特性.
3 结论1) 应用模糊数学理论的思想建立了一类适用于某些特定性质的对象的评价模型.通过对这类对象的性质的分析,给出了一个非线性的模糊隶属函数来描述其评估.与传统的隶属函数相比,这一隶属函数有更好的光滑性.
2) 将这类模型应用于通信卫星的效能评估上,基于具体数据给出了具体的评价函数,从而得到东方红系列通信卫星的效能评估.
| [1] |
安雪滢, 赵勇, 杨乐平, 等. 基于模糊理论的卫星系统效能评估仿真研究[J]. 系统仿真学报, 2006, 18(8): 2334-2337. |
| [2] |
冯书兴, 肖业伦, 陈浩光. 基于模糊推理的卫星系统综合效能评估方法[J]. 中国空间科学技术, 2003, 23(1): 31-37. |
| [3] |
杨军. 基于模糊理论的卫星导航系统综合效能评估研究[J]. 宇航学报, 2004, 25(2): 147-151, 194. |
| [4] |
胥伟, 徐慨, 钟帅. 基于AHP灰色效能法的同步轨道通信卫星综合能力评估[J]. 船电技术, 2012, 32(11): 13-15, 18. DOI:10.3969/j.issn.1003-4862.2012.11.004 |
| [5] |
曹加勇. 基于TOPSIS的同步轨道通信卫星综合能力评估[J]. 指挥控制与仿真, 2011, 33(1): 61-63. |
| [6] |
尹江丽, 王莉. 军用卫星通信系统效能评估指标体系研究[J]. 兵工自动化, 2008, 27(6): 9-11. |
| [7] |
王力, 刘家琦. 假设检验在AHP及卫星方案优选中的应用[J]. 系统工程与电子技术, 2001, 23(12): 49-52. DOI:10.3321/j.issn:1001-506X.2001.12.015 |
| [8] |
毛晓芳, 岳晓蕊, 傅惠民. 通信卫星推力器可靠性评估方法[J]. 航空动力学报, 2011, 26(11): 2475-2479. |
| [9] |
黄小钰, 李智. 基于MAS的通信卫星系统整体效能评估方法[J]. 装备指挥技术学院学报, 2012, 23(1): 89-93. |
| [10] |
杨巧丽, 叶淦华, 陆锐敏. 基于糊糊理论的星座通信系统性能综合评估[J]. 无线电通信技术, 2009, 35(3): 8-10. |
| [11] |
杨柳, 张宁. 卫星话音通信网运行质量指标体系研究与评估[J]. 通信技术, 2014, 47(3): 286-289. |
| [12] |
刘旭光, 孔德强, 李浩, 等. 一种卫星通信系统效能评估方法研究[J]. 航天电子对抗, 2012, 28(5): 30-33, 52. |
| [13] |
陈浩光, 李云芝, 孙磊. 基于模糊推理的武器系统效能评估新方法[J]. 军事运筹与系统工程, 2004, 18(4): 63-68. |
| [14] |
吴际, 矫贺明, 石春生. 基于模糊理论的R&D员工创新绩效评价模型[J]. 管理学报, 2011, 8(5): 734-738. |
| [15] |
谢季坚, 刘承平. 模糊数学方法及其应用[M]. 3版. 武汉: 华中科技大学出版社, 2006: 1-89.
|
 2016, Vol. 48
2016, Vol. 48