垂直轴潮流能水轮机是获取潮流能的重要装置[1-2], 其自启动性能是关系到水轮机年发电量的关键参数,也是评价发电机组性能优劣的重要指标之一[3-4].对于垂直轴叶轮的自启动性能研究最早始于风力发电机,1985年Rajaoferson等[5]通过实验证明Darrieus型风力机具有一定的自启动性能.Kirke[6-7]等详细阐述了垂直轴风力机的自启动性能,指出固定偏角垂直轴风力机一个最大的局限性就是自启动性能差,并提出了几种改进方式.随着计算机的快速发展以及CFD软件的日渐成熟,2010年开始, 研究者们纷纷采用数值算法来研究垂直轴叶轮的启动性能.例如Beri等[8]利用CFD软件计算得到NACA2415翼型变弧固定叶片垂直轴风力机具有自启动性能的结论;李凤来等[9]通过加装叶栅附体使潮流能垂直轴水轮机的自启动性能得到进一步加强; Batista等[10-11]通过研究EN0005新型叶片和NACA系列不对称翼型的流体性能使垂直轴风力机具有一定的自启动性能;张新建等[12]研究了固定偏角垂直轴风力机的安装半径、叶片弦长和来流速度对自启动性能的影响.以上数值研究都是基于稳态研究,即在给定均匀流的状态下,研究风(水)轮静止不动的状态下,叶片对主轴产生的静力矩; 2011年,张学伟等[13]利用Fluent软件实现了潮流能水轮机自启动过程的瞬态数值模拟;Untaroiu等[14]应用CFX CEL Expression语言实现了垂直轴风力机二维和三维的瞬态自启动过程模拟,并对比了湍流度、时间步等参数设置对计算精度的影响,但上述研究者们都没有分析叶轮的启动位置(初始方位角)对于自启动过程的影响.
本文着重研究垂直轴水轮机的初始方位角对于启动性能的影响.首先分析三叶片固定偏角垂直轴水轮机处于不同方位角时叶片对主轴的稳态启动力矩;然后采用CFX软件的rigid-body模块实现了水轮机自启动过程的刚体-流体耦合瞬态数值模拟;最后对应稳态启动力矩曲线,探讨启动位置对于瞬态启动时间和转速稳定性的影响.
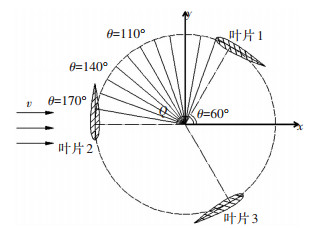
1 数值模型 1.1 模型参数及坐标系本文采用李志川[15]研发的垂直轴水轮机试验模型作为研究对象,模型参数见表 1.水轮机坐标系定义如图 1所示,图 1中笛卡尔坐标系原点位于主轴中心,x轴方向平行于来流方向,y轴方向与x轴正交;θ为叶片的方位角,取x轴为起点逆时针旋转为正;Q为叶片对主轴的合力矩.
| 表 1 李志川[15]垂直轴水轮机模型参数 |
|
图 1 水轮机坐标系 |
CFX软件通过求解NS方程解决黏性流体问题,不可压缩黏性流体的连续性方程和RANS方程组为:
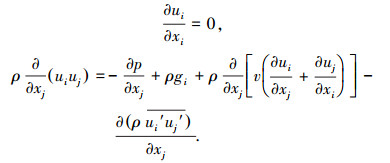
|
式中:ui、uj分别为速度分量时均值,i,j=1,2,3;p为压力时均值;ρ为流体密度;v为流体黏性系数;gi为重力加速度分量;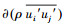
水轮机叶片刚体运动控制方程组为:
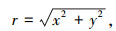
|
(1) |
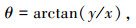
|
(2) |
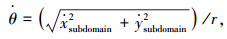
|
(3) |
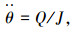
|
(4) |
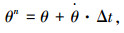
|
(5) |
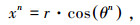
|
(6) |
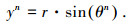
|
(7) |
式中:x、y分别为叶片局部坐标系内的节点坐标;θ为叶片的方位角;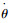
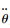
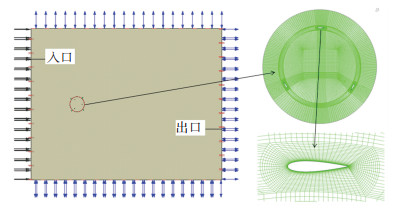
采用CFX13.0全隐式耦合算法求解黏性流体控制方程,流体和刚体运动控制方程的耦合采用Rigid body模块完成.计算域和网格如图 2所示,叶轮所在区域为旋转域,外部区域为静止域,采用结构化网格,内外域交界面采用滑移网格技术.流场入口设定为均匀流速1 m/s,5%湍流强度,上下边界和出口设定为开放出口,绝对压力为101 325 Pa,叶片表面设定为无滑移壁面.湍流模型为SST模型.稳态的最大迭代步为200,物理时间为0.3 s;瞬态计算的时间步长为0.01 s.
|
图 2 模型计算域及网格 |
由于李志川[15]水轮机模型没有进行启动性能的测试,为了验证计算模型的精度,本文采用文献[14]中英国Durham大学的垂直轴风力机的二维计算模型作为验证算例(模型参数见表 2).在保证计算域和边界条件相同的基础上,计算了启动过程中转速随时间的变化曲线,并与文献[14]中的二维结果进行了对比.
| 表 2 Durham垂直轴风力机模型参数 |
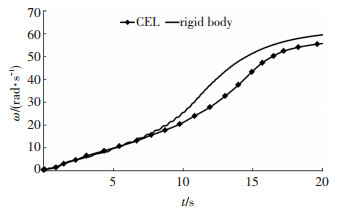
图 3给出启动过程的转速变化对比曲线,可以看到,在初始阶段自启动角速度数值接近,在10 s之后数值出现偏差,两条曲线的最大误差为7.3%.产生误差的原因主要有:
|
图 3 启动过程中叶轮瞬时转速随时间的变化 |
1) Untaroiu的网格总数为13.6万,Y+=1.7;本文受限于计算条件,网格总数降到9.8万,Y+=1.9.
2) 文献[14]采用的是CEL Expression语言来实现流体-刚体运动耦合,是一种显式算法;而本文采用的是rigid body模型来实现流体-刚体运动耦合,是一种全隐式算法.
3) 显式算法离散格式的稳定性取决于时间步和空间步的选取,文献[14]对比了时间步对计算结果的影响,选取dt=0.001 s;由于全隐式算法无条件稳定,为了节约计算成本,本文在保证收敛性的基础上选取dt=0.01 s.
整体来看,两条曲线的变化规律一致,都是随着时间的增加转速逐渐爬升,0~10 s之内几乎呈线性变化,10~15 s之间转速爬升加速,超过15 s之后转速爬升回缓,接近20 s时转速接近最大值.这说明无论应用CFX软件的rigid body模块还是应用CEL Expression语言,在定性上讨论瞬态自启动过程的变化规律都是可行的.
3 结果和讨论本文首先讨论叶片处于不同的初始位置时,对主轴的静态力矩.采取两种方法计算静态力矩:
1) 利用NACA0018翼型升阻力系数的静态试验值,推导出叶片在不同方位角下的切向力,然后叠加3个叶片切向力总和从而计算出叶片对主轴的合力矩.
2) 采用稳态模型,应用CFX软件模拟水轮机叶片在不同初始位置时的流场,待计算收敛后统计3个叶片对主轴的合力矩.如图 1所示,由于3个叶片沿圆周对称分布,本文取叶片1在θ= 60°~170°之间的位置进行分析,每间隔10°为一个工况.为了数据分析的方便,定义水轮机的速比和力矩系数如下:
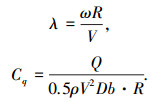
|
式中:ρ为介质密度;b为叶片展长(二维计算展长取单位为1);R为水轮机半径.
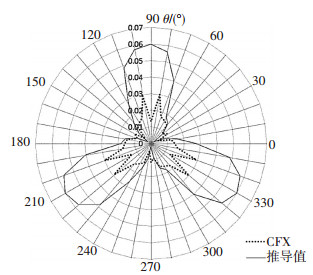
图 4给出两种计算方法得到的水轮机主轴的静态力矩系数对比.可以看到水轮机力矩推导值相较于CFX的稳态计算值偏大,这是因为用升阻力系数推导叶片受力时,假定叶片之间无干扰;但用CFX建立数值模型时,可以充分考虑上游叶片对下游叶片流场的影响,这种影响在大部分的位置角时会导致下游叶片的入流速度损失,因此CFX的计算值更符合真实的流场特性.整理来看,固定偏角垂直轴水轮机的静态力矩值都很小,但在阻尼为零的假定下,只要力矩不出现零值或负值,根据式(1)~(7),理论上就可以实现叶轮启动过程的瞬态模拟.
|
图 4 不同方位角下水轮机的静态力矩系数 |
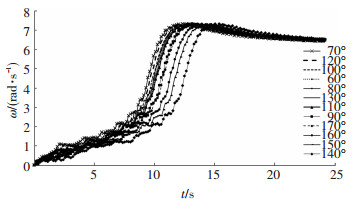
图 5为水轮机在不同初始方位角时启动过程中角速度(ω)随时间(t)的变化曲线.图 5中曲线证实了公式分析的结论,在系统零阻尼的假定条件下,水轮机在各个初始方位角时都具有自启动性能,且旋转角速度最终都稳定在6.5 rad/s左右.无论初始方位角在什么位置,曲线的变化趋势相同,叶轮的角速度从线性爬升阶段过渡到爬升速度加剧阶段,经过速度回落阶段最终达到稳定值.由于初始方位角的不同,角速度的爬升速度和达到的最大值也有所不同.方位角在θ=70°时水轮机自启动角速度达到最大值用时最短.在θ=60°、70°、80°、100°、110°、120°以及130°的位置,自启动角速度的变化曲线相近,到达各自最大值的用时相对其他5种工况少,属于优选自启动方位角范围.在θ=90°、140°、150°、160°和170°的位置,自启动角速度到达最大值用时相对较长,其中θ=140°的自启动时间最长,这5个位置属于次选自启动方位角.
|
图 5 启动过程中角速度随时间的变化曲线(θ=60°~170°) |
在t=13~24 s阶段各角速度从最大值回落到稳定值.θ=140°用时最长且角速度最大值时间节点排在最后,θ=70°用时最短且角速度最大值时间节点排在最前面.优选自启动方位角回稳的用时相对次选自启动方位角回稳用时要小,会更快达到稳定值.对应图 4的CFX静态力矩曲线看出,140°是静态力矩最小的位置,所以启动速度最慢;150°、160°和170°位置的静态启动力矩均低于优选启动方位角的静态力矩.因此可以判断,水轮机的静态启动力矩是影响水轮机启动性能的重要因素.在优选自启动方位角的范围内,即θ=60°~130°之间,θ=90°位置的静态力矩出现了一个突降的阶跃.如图 6所示,此时叶片位置的分布比较特殊,叶片3完全处于叶片2的尾流区域内,叶片2脱落的尾涡对于叶片3近前方的合速度产生很大的影响,导致叶片3对启动力矩做出零贡献甚至是负贡献,这是在初始启动位置中应避免的一个特殊方位角.

|
图 6 稳态流场速度分布图(θ=90°) |
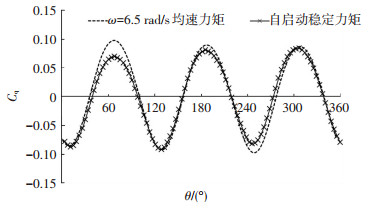
从图 5中可以看出,任何初始方位角下启动,叶轮的角速度最终都稳定在6.5 rad/s左右.在来流速度不变的情况下,水轮机以角速度ω=6.5 rad/s做均速旋转,计算结果显示平均力矩系数Cq为0,证明了ω=6.5 rad/s为该流速下叶轮的飞逸转速.图 7给出水轮机以恒定转速ω=6.5 rad/s做均速旋转时的力矩系数与自启动状态下转速达到6.5 rad/s时力矩系数的对比,两条曲线基本吻合,恒定转速计算的曲线波动比自启动瞬态计算的波动略高,均值都为0.由式(6)可以推断,当无阻尼状态下叶轮自由旋转时,转速达到稳定即为叶轮的角加速度为0,此时叶片对主轴的合力矩均值必为0.也就是说,无阻尼状态下水轮机自启动过程达到的角速度稳定值必为水轮机的飞逸转速值.以往在进行转速恒定假设数值模拟的时候,需要不断改变速比点来寻求飞逸转速的位置,应用本文的自启动数值模拟方法可以估算出在不同流速下水轮机模型的飞逸转速.
|
图 7 力矩系数随方位角变化曲线 |
1) 应用CFX的rigid body模块,可实现固定偏角垂直轴水轮机的刚体-流体耦合瞬态自启动过程的数值模拟,应用该方法可以估算出在不同流速下水轮机的飞逸转速.
2) 三叶片固定偏角垂直轴水轮机的静态启动力矩在所有方位角下均大于零,因此在系统零阻尼的条件下,水轮机在所有的初始方位角下都具有自启动性能.
3) 方位角θ=60°~130°属于优选自启动范围,其中θ=90°由于流场的特殊性,自启动性能较差;方位角θ=140°~170°属于次选自启动范围角,其中θ=140°为最差自启动方位角,静态启动力矩最小,自启动用时最长,应尽量避免在启动时刻叶片处于该位置.
| [1] |
李志川, 张亮, 孙科, 等. 垂直轴潮流水轮机数值模拟研究[J]. 太阳能学报, 2011, 32(9): 1321-1326. |
| [2] |
AJEDEGBA J O, NATERER G F, ROSEN M A, et al. Effects of blade configurations on flow distribution and power output of a zephyr vertical axis wind turbine[C]//Proceedings of the 3rd IASME/WSEAS International Conference on Energy & Environment. Stevens Point, Wisconsin: World Scientific and Engineering Academy and Society, 2008: 480-486.
|
| [3] |
王世澎. 波浪对潮流影响的数值模拟研究[D]. 大连: 大连理工大学, 2007: 20-22.
|
| [4] |
HE Huanyu, SUN Ke, MA Yong, et al. Self-starting performance numerical analysis of fixed-pitch vertical axis hydro-turbine[C]//Proceedings of the 2nd International Conference on Energy Engineering and Environment Engineering. Pfaffikon: Trans Tech Publications, 2014: 102-105.
|
| [5] |
RAJAOFERSON S, COMOLET R. Self-starting process of the Darrius wind-turbine[C]//European Wind Energy Conference. [S. l. ]: [s. n. ], 1985: 523-528.
|
| [6] |
KIRKE B K. Evaluation of self-starting vertical axis wind turbines for seand alone applications[D]. Australia: School of Engneering, Griffith University, 1998: 41-50.
|
| [7] |
KIRKE B K, LAZAUSKAS L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pith[J]. Renewable Energy, 2011, 36(3): 893-897. DOI:10.1016/j.renene.2010.08.027 |
| [8] |
BERI H, YAO Yingxue. Effect of camber airfoil on self-starting of vertical axis wind turbine[J]. Journal of Enviromental Science and Technology, 2011, 4(3): 302-312. DOI:10.3923/jest.2011.302.312 |
| [9] |
李凤来, 姜德志, 孟巧. 竖轴固定直叶片潮流水轮机自启动性能研究[J]. 工程与实验, 2011, 51(3): 23-26. |
| [10] |
BATISTA N C, MELICIO R. MATICS J C O, et al. New blade profile for darrieus wind turbines capable to self-start[C]//IET Conference on Renewable Power Generation, RPG 2011. Edinburgh: Institution of Engineering and Tech-nology, 2011: 1-5.
|
| [11] |
BATISTA N C, MELICIO R, MATICS J C O, et al. Self-start evaluation in lift-type vertical axis wind turbines: methodology and Computational tool applied to asymmetrical airfoils[C]//International Conference on Power Engineering, Energy and Electrical Drives (POWERENG). Malaga: IEEE Computer Society, 2011: 1-6.
|
| [12] |
张新建, 蔡新, 潘盼. H型垂直轴风力机启动性能分析[J]. 水电能源科学, 2013, 31(5): 243-246. |
| [13] |
张学伟, 张亮, 李志川, 等. 垂直轴自由变偏角水轮机的多体耦合数值求解方法[J]. 计算力学学报, 2013, 30(3): 370-375. DOI:10.7511/jslx201303009 |
| [14] |
UNTAROIU A, WOOD H G, ALLAIRE P E, et al. Investigation of self-starting capability of vertical axis wind turbines using a computational fluid dynamics approach[J]. Journal of Solar Energy Engineering, 2011, 133(4): 112-120. |
| [15] |
李志川. 垂直轴潮流能水轮机水动力特性数值模拟与实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2011: 35-36.
|
 2016, Vol. 48
2016, Vol. 48




