2. 哈尔滨工程大学 航天与建筑工程学院, 150001 哈尔滨
2. College of Aerospace and Civil Engineering, Harbin Engineering University, 150001 Harbin, China
中国变分原理学家、中科院院士刘高联在为本文作者的一部专著撰写序言时指出[1]:各种自然现象和过程(特别是力学现象)通常由一组数理方程(偏微分方程、积分-微分方程或积分方程)及初、边值条件来描述,但人们通过长期的探索研究,发现这些现象和过程常常使系统的某一整体量(泛函)取驻值或极值,因而又可以用相应的变分原理来描述.后一描述法的突出优点是:1)数学形式简单紧凑,但内含却甚丰富(包含了全部数理方程及初边值条件组); 2)是整体性描述,包括各种物理间断面上的相容条件; 3)有‘变域变分’、‘自然边界条件’等特殊工具,能够自动捕获各种未知边(分)界面; 4)是各种变分直接解法和有限元法的理论基础.可见,变分原理既体现了数学形式上的简洁优美,又体现了物理内容上的丰富深刻,更具有工程应用上的价值,确实代表了数学与物理的交融与贯通,以及理论与实用的结合与统一.特别是自上世纪60年代起,有限元素法的兴起与蓬勃发展,使其作为主要理论基础的变分原理又重新焕发了青春,取得了长足的发展.
从应用有限元素法进行近似计算的角度看问题,以弹性力学为例,弹性力学有3类基本条件——平衡关系(含力学边界条件)、连续关系(含位移边界条件)和本构关系;最小势能原理需要精确满足连续关系和本构关系2类基本条件,可以近似满足平衡关系1类基本条件;最小余能原理需要精确满足平衡关系和本构关系2类基本条件,可以近似满足连续关系1类基本条件.
我国学者[2-4]对于以上事实有几种不同的说法,有的学者称为,最小势能原理可以近似满足平衡关系,最小余能原理可以近似满足连续关系;也有的学者称为,最小势能原理平衡关系次要,最小余能原理连续关系次要;还有的学者称为,最小势能原理反映的规律为平衡关系,最小余能原理反映的规律为连续关系.本文采用最后一种说法来研究问题.
Reissner[5]的弹性力学二类变量的广义变分原理的问世,说明国外学者也有类似的认识,在弹性力学的3类基本规律中,最小势能原理反映的规律为平衡关系,最小余能原理反映的规律为连续关系,文献[5]中二类变量的广义变分原理反映平衡关系和连续关系2类基本规律.
是否可以建立一个变分原理反映平衡关系、连续关系和本构关系3类基本规律呢?这就是胡海昌—鹫津久一郎三类变量广义变分原理的“Idea”[4, 6].
以上的学术思想既适用于保守系统又适用于非保守系统[7-9],既适用于弹性力学又适用于一般力学[10-12],既适用于边值问题又适用于初值问题[13-15]力学,同时也适用于流体力学[16-17],电磁学[18-19],….本文在继承上述学术思想和总结变分原理的研究成果的基础上,论证了弹性力学变分原理的各类条件的完备性[20],得到了刘高联院士的充分肯定.变分原理泛函的先决条件和驻值条件一起,构成一个适定的微分方程组,这便是变分原理的各类条件完备性的第1种含义.变分原理的先决条件、补充条件及反映的规律一起构成弹性力学的全部基本方程,这便是变分原理的各类条件完备性的另一种含义.
由以上论述可见,在广义变分原理中,已经有胡海昌-鹫津久一郎广义变分原理反映平衡关系(含力学边界条件)、连续关系(含位移边界条件)和本构关系3类基本规律,但是,在经典变分原理中只有最小势能原理反映的规律为平衡关系和最小余能原理反映的规律为连续关系,尚未见反映的规律为本构关系的变分原理.本文以非线性弹性力学为例,建立反映的规律为本构关系的变分原理具有一定的深度和难度,不失一般性.为叙述方便,不妨将反映的规律为本构关系的变分原理称为本构变分原理.本文应用变积方法建立非线性弹性动力学的Hamilton原理,应用对合变换[21],由非线性弹性动力学的Hamilton原理推导出非线性弹性动力学的本构变分原理,应用Lagrange乘子法和局部代入法论证了非线性弹性动力学的本构变分原理反映的规律为本构关系[22].
1 非线性弹性动力学的Hamilton原理应用Cartesian张量,非线性弹性动力学的基本方程如下.
1) 动态平衡关系:
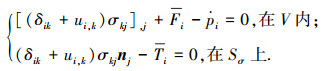
|
(1) |
2) 连续关系:

|
(2) |
3) 本构关系:

|
(3) |
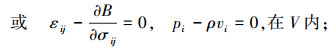
|
(4) |
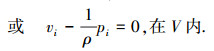
|
(5) |
4) 时间边值条件[23]:
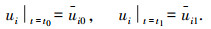
|
(6) |
式中:A为应变能函数;B为余应变能函数;Sσ为力边界面;Su为位移边界面;V为体积;Fi为体力;Ti为面力;ui为位移;σij为应力;εij为应变;pi为动量;vi为速度;ρ为质量密度;nj为法向矢量;“,”为对空间坐标变量的导数.
将虚位移δui乘上式(1),然后积分,并代数相加,可得
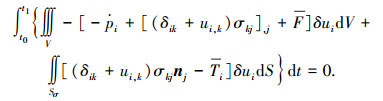
|
(7) |
应用Green定理和分部积分可得:

|
(8) |
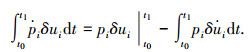
|
(9) |
将式(8)和式(9)代入式(7),按惯例,在时域边界上取δui=0,可得
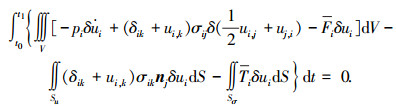
|
将式(1)和式(2)代入式(10),可得
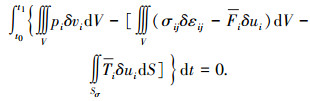
|
(10) |
将本构关系式(3)和式(4)代入式(10),可得
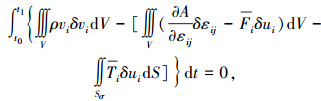
|
(11) |
式(1)可以处理为一个泛函的驻值问题
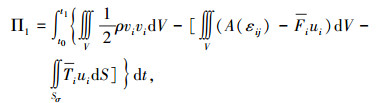
|
其先决条件为式(2).实际上,这即是非线性弹性动力学中的Hamilton原理[24].
2 反映的规律为本构关系的变分原理应用对合变换,Hamilton原理的泛函可以变换为
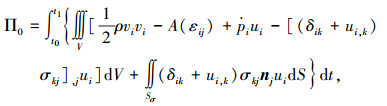
|
其先决条件为式(1)和式(2).
本文将应用两种不同的方法,论证这是一个反映的规律为本构关系的变分原理,称之为本构变分原理.
2.1 应用Lagrange乘子法推导本构变分原理的驻值条件[25-26]将Π0变分,并令δΠ0=0,可得
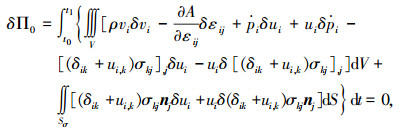
|
其先决条件的变分式为:
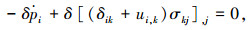
|
(12) |
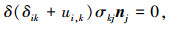
|
(13) |
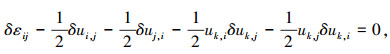
|
(14) |
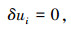
|
(15) |
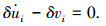
|
(16) |
引入Lagrange乘子,将式(12)~(16)纳于泛函δΠ0中,可得
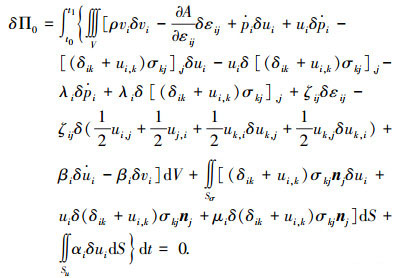
|
(17) |
应用Green定理和分部积分可得:
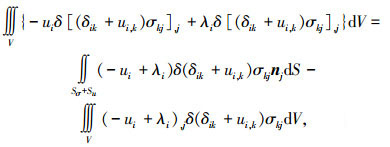
|
(18) |
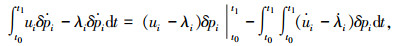
|
(19) |
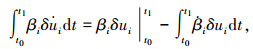
|
(20) |

|
(21) |
将式(18) ~(21)代入式(17),按惯例在时域边界处取δui=0,经整理可得
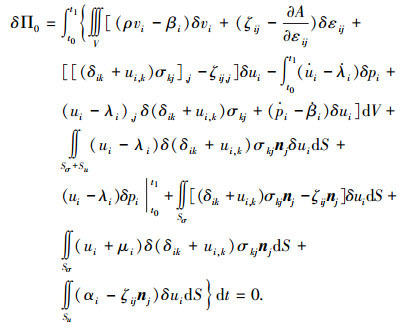
|
(22) |
由于引入Lagrange乘子,使得各虚量相互独立,故由式(22)可得:

|
(23) |
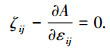
|
(24) |
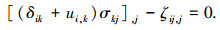
|
(25) |
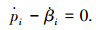
|
(26) |
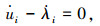
|
(27) |
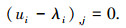
|
(28) |
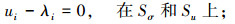
|
(29) |
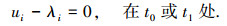
|
(30) |
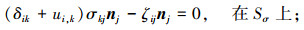
|
(31) |
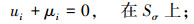
|
(32) |
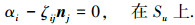
|
(33) |
由式(25), 式(31)解得
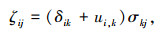
|
(34) |
由式(27)~(30)解得

|
(35) |
由式(26)解得
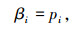
|
(36) |
由式(32)解得
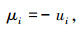
|
(37) |
由式(33)解得
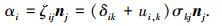
|
(38) |
将式(34)~式(38)代入式(17),整理可得
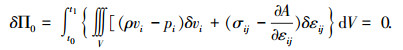
|
(39) |
由式(39)可得Π0的驻值条件为:
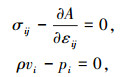
|
可见,这个变分原理反映的规律为本构关系.
2.2 应用局部代入法推导本构变分原理的驻值条件应用对合变换Hamilton原理的泛函变换为本构变分原理泛函为
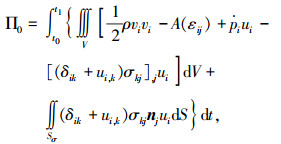
|
(40) |
其先决条件为式(1)和式(2).
将Π0变分,并令δΠ0=0,可得
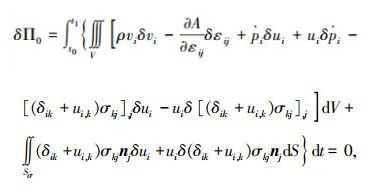
|
(41) |
其先决条件的变分式为式(12)~(16),将式(12)~(16)代入式(41),可得
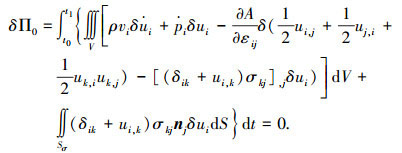
|
(42) |
应用Green定理和分部积分可得:
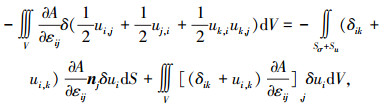
|
(43) |

|
(44) |
将式(43)~(44)代入式(42),然后将式(15)代入式(42),并按惯例在时域边界处取δui=0,可得
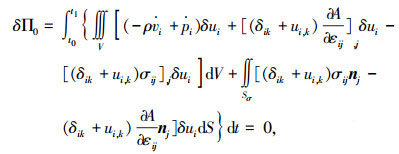
|
(45) |
由于δui的任意性,由式(45)可得本构变分原理驻值条件的一种表达形式:
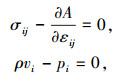
|
这便又一次表明,这个变分原理反映的规律为本构关系.
3 结论1) 通过变积方法,由非线性弹性动力学的基本方程建立了非线性弹性动力学Hamilton原理,即本构变分原理, 为下一步证明奠定了基础.
2) 通过对合变换方法,分别应用Lagrange乘子法和局部代入法推导本构变分原理的驻值条件,得到了本构关系表达式,证明了本构变分原理反映的规律为本构关系.
3) 从理论上说,补充和完善了前人研究的经典变分原理对3类基本规律的反映, 从工程应用上说,为数值建模提供了依据.
| [1] |
梁立孚. 变分原理及其应用[M]. 哈尔滨: 哈尔滨工程大学出版社, 2005.
|
| [2] |
钱令希. 余能理论[J]. 中国科学, 1950, 1(1/2): 449-456. |
| [3] |
钱伟长. 弹性理论中广义变分原理的研究及其在有限元计算中的应用[J]. 力学与实践, 1979, 1(2): 18-27. |
| [4] |
HU Haichang. On some variational principles in the theory of elasticity and the theory of plasticity[J]. Scientia Sinica, 1954, 10(3): 259-290. |
| [5] |
REISSNER E. On a variational theorem in elasticity[J]. Journal of Mathematics and Physics, 1950, 29(1): 90-95. |
| [6] |
WASHIZU K. On the variational principles of elasticity and plasticity: Technical Report: 25-18[R]. Massachusetts: Massachusetts Institute of Technology, 1955.
|
| [7] |
LEIPHOLZ H H E. On some developments in direct methods of the calculus of variations[J]. Applied Mechanics Reviews, 1987, 40(10): 1379-1392. DOI:10.1115/1.3149540 |
| [8] |
刘殿魁, 张其浩. 弹性理论中非保守问题的一般变分原理[J]. 力学学报, 1981, 17(6): 562-570. |
| [9] |
LIANG Lifu, LIU Diankui, SONG Haiyan. The generalized quasi-variational principles of non-conservative systems with two kinds of variables[J]. Science in China G:Physics and Astronomy, 2005, 48(5): 600-613. DOI:10.1360/04yw0139 |
| [10] |
ZHU Ruzeng. Variational principle of second, first and intermediate kinds for non-holonomic mechanics[J]. Science in China Series A:Mathematics, 1999, 42(5): 546-551. DOI:10.1007/BF02882251 |
| [11] |
梁立孚, 罗恩, 冯晓九. 分析动力学初值问题的一种变分原理形式[J]. 力学学报, 2007, 39(1): 106-111. |
| [12] |
LIANG Lifu, HU Haichang. Generalized variational principle of three kinds of variables in general mechanics[J]. Science in China(Series A), 2001, 44(6): 770-776. |
| [13] |
GURTIN M E. Variationnal principles for elastodynamics[J]. Archive for Rational Mechanics and Analysis, 1964, 16(1): 34-50. DOI:10.1007/BF00248489 |
| [14] |
LUO En. Gurtin-type variational principles in linear elastodynamics[J]. Scientia Sinica (Series A), 1988, 31(3): 298-312. |
| [15] |
梁立孚, 罗恩, 刘殿魁. 非保守弹性动力学初值问题的简单Gurtin型拟变分原理[J]. 固体力学学报, 2007, 28(3): 224-228. |
| [16] |
钱伟长. 粘性流体力学的变分原理和广义变分原理[J]. 应用数学和力学, 1984, 5(3): 305-322. |
| [17] |
梁立孚, 石志飞. 粘性流体力学的变分原理及其广义变分原理[J]. 应用力学学报, 1993, 10(1): 119-123. |
| [18] |
梁忠宏, 梁忠伟. 电磁场理论边值问题的变分原理及广义变分原理[J]. 哈尔滨工业大学学报, 1995, 27(2): 68-74. |
| [19] |
梁忠宏, 刘树东. 电磁场理论初值问题的变分原理及广义变分原理[J]. 哈尔滨工业大学学报, 1998, 30(3): 68-70, 76. |
| [20] |
梁立孚, 冯晓九, 宋海燕. 论弹性力学变分原理各类条件的完备性[J]. 哈尔滨工程大学学报, 2004, 25(2): 153-156. |
| [21] |
CHIEN Weizang. Involutory transformations and variational principles with multi-variables in thin plate bending problems[J]. Applied mathematics and Mechanics, 1985, 6(1): 25-39. DOI:10.1007/BF01895680 |
| [22] |
李跃军. 关于已识别拉氏乘子法和一个非线性弹性理论的广义变分原理[J]. 北京建筑工程学院学报, 1988(1): 34-40. |
| [23] |
刘世奎. 弹性动力学Gurtin型广义变分原理[J]. 北京建筑工程学院学报, 1991(1): 1-8. |
| [24] |
刘世奎. 弹性动力学Hamilton型广义变分原理[J]. 北京建筑工程学院学报, 1992(1): 9-17. |
| [25] |
冯晓九, 梁立孚. 功率型变分原理和功能型拟变分原理[J]. 应用数学和力学, 2015, 36(11): 1178-1190. DOI:10.3879/j.issn.1000-0887.2015.11.006 |
| [26] |
冯晓九, 梁立孚, 宋海燕. 航天充液系统耦合动力学的功能型拟变分原理[J]. 中国科学:技术科学, 2016, 46(2): 195-203. |
 2016, Vol. 48
2016, Vol. 48


