2. 金川集团股份有限公司, 737104 甘肃 金昌;
3. 北京地质研究所, 100120 北京
2. Jinchuan Group Co. LTD. 737104 Jinchang, Gansu, China;
3. Beijing Institute of Geology, 100120 Beijing, China
地应力是存在于地层中的天然应力,是导致工程变形破坏和地质灾害的内动力,是地下工程稳定性分析和灾害防控必须考虑的重要因素之一[1-5].由于地质体在漫长的地质构造运动中经历多次地质作用和改造演化,在地层内封存不同时期的残余应力,因此地质构造类型、作用程度和方向不同,导致地应力场的大小和方向存在时间和空间的变异性.由此给工程岩体的地应力场反演带来极大困难,一直是岩土工程稳定性分析长期研究而未能解决的技术难题,是地质工程研究的课题之一.
20世纪80年代首次提出黏弹性位移反分析法,根据围岩变形监测信息和理论分析方法进行岩体参数和地应力反演.但黏弹塑性位移反分析存在的多解问题一直未能得到很好解决[6].随着人工智能的发展,基于神经网络与数值分析方法相结合的地应力反演研究取得进展,但该种地应力反演仅仅将有限的地应力测量样本进行外延和非线性回归,仍难以解决复杂工程地质体的真实地应力场反演问题[7-13].地应力现场测量是获得地应力的重要手段之一,通常根据工程范围、重要性以及复杂程度,开展有限的地应力测量工作,并在此基础上进行统计回归分析,由此获得研究范围内的地质体主应力大小和方向[14-19].但由于受时间和经费限制,大部分工程地应力测量不仅数量有限,且受测量手段以及复杂因素影响,通常获得地应力测试结果存在很大程度的离散性,由此给地应力研究和工程应用带来很多困难,直接影响地质工程稳定性的定量分析及工程优化设计.研究发现,目前地质体地应力研究大多集中于有限地质体的统计回归和宏观规律.换句话说,通过有限个地应力测量或结合地质构造形迹分析,给出表征有限范围内的地质体中的地应力特征(侧压系数和主应力方向).众所周知,复杂地质体经历多次地质构造运动,在地质体内封存不同时期的构造应力,导致地应力场存在很大的变异性.以致实测的有限地应力信息难以真实表征实际地应力.
近年来考虑到工程地应力特征的复杂性,结合地质构造形迹以及围岩变形破坏特征进行地应力场识别,是目前复杂地质体地应力研究的发展动向[20-23],但该种方法还局限于定性分析.本文将利用有限个典型和可靠的地应力测量结果,采用数值分析与遗传规划相结合,建立地质体的岩体参数和侧压系数的优化数值模型,直接反演复杂地质体的地应力场,而不是通过求得有限地质体的侧压系数和主应力方向来表征地应力特征.该方法能够考虑复杂地质体的地应力场所固有的空间变异性,根据工程岩体的岩性进行地应力场分区反演.由此获得工程岩体的地应力场能够与工程岩体数值分析实现无缝连接,从而提高数值分析方法在地质工程中应用的实用性与可靠性.
1 工程地质体地应力场智能反演方法 1.1 地应力现场测量采用地应力测量技术,获得工程地质体内的n个地应力测点的地应力测量值为
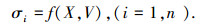
|
式中:σi为地应力测量值;X= {xi,yi,zi}T为地应力测点的空间位置坐标;V= {σ1i,σ2i,σ3i,α1i,α2i,α3i }T为地应力3个主应力和主应力方向.
1.2 地应力影响函数建立地质体中的地应力是在地质构造作用过程中,封存于岩体中的残余应力,与区域构造应力和岩体特性密切相关.因此根据实测的n个地应力的测点位置(X={xi,yi,zi}T),采用正交数值分析,建立地应力测点位置处的地应力与岩体参数和侧压系数的影响函数.具体实施步骤如下.
1) 建立三维数值分析模型.根据地质体的岩性和区域地应力构造特征,首先对地质体进行分区,然后利用三维数值分析系统(例如FLAC3D),建立包含n个地应力测点的工程地质体三维数值模型.
2) 正交数值分析设计.考虑地应力赋存条件与构造状态,选择影响地应力特征的因素和水平.考虑到地应力通常赋存于未受工程影响的原岩中,其岩体力学性质基本上处于弹性状态,因此根据工程地质分区,选择不同分区的岩体密度γi、弹性模量Ei和泊松比μi, i=1,m(其中m为工程地质体分区数)以及水平方向的侧压系数λ1、λ2作为地应力分布特征的影响因素;借助工程经验或岩体分类,分别给出各个分区岩体的力学参数和地应力参数的变化范围,由此确定地应力影响因素的设计水平.在此基础上,采用正交设计表进行三维正交数值分析的方案设计.
3) 三维正交数值分析.根据正交数值分析方案,逐一进行地质工程体的三维数值分析.根据每一计算方案和地应力测点的位置坐标X={xi,yi,zi}T,提取n个测点的地应力计算值V′i={σ′1i, σ′2i, σ′3i, α′1i, α′2i, α′3i}T,i=1,n(其中n为工程地质体地应力测点数).
1.3 建立地应力影响函数以正交数值分析方案中的岩体参数和侧压系数作为自变量,以提取的地应力计算值作为因变量进行统计回归或智能分析,建立地应力与岩体参数和侧压系数之间的函数关系为
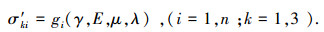
|
式中:σ′ki为第i个地应力测点的第k个主应力,gi(·)为第i个地应力测点的第k个主应力函数.
1.4 建立地应力场反演优化模型1) 建立地应力场反演目标函数.以n个测点的地应力测量值σi与对应的计算值σ′ki之差的平方和达到最小值为优化目标,建立工程地质体地应力场反演优化模型为
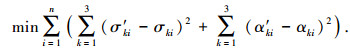
|
(1) |
2) 确定地应力场反演优化模型的约束条件.根据工程地质体的不同分区岩体参数和侧压系数的范围,确定工程地质体地应力场反演优化模型的约束条件为:
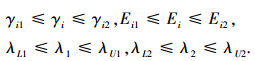
|
(2) |
式中:γi、Ei分别为工程地质体第i个分区的岩体密度和弹性模量;λ1、λ2分别为三维数值模型的两个水平方向的侧压系数;γi1,γi2分别为第i个分区的岩体密度上、下限;Ei1,Ei2分别为第i个分区的岩体弹性模量上、下限.
1.5 工程地质体地应力场反演优化模型求解考虑到地应力场反演优化目标函数属于高度非线性函数,因此采用遗传算法对由式(1)和式(2)确定的优化模型进行求解,由此获得与原岩地应力场所对应的不同分区地质体的岩体参数和侧压系数.
1.6 工程地质体的地应力场反演将求解的工程地质体岩体参数和侧压系数,代入三维数值分析模型进行正分析,由此获得的应力场即为工程地质体初始地应力场.
2 金川矿区工程地质体地应力场反演为阐述基于有限个地应力测量值进行工程地质体地应力场反演方法,以金川矿区为工程背景进行实例分析.金川镍矿是世界上著名的多金属共生大型硫化铜镍矿床,位于我国甘肃省河西走廊龙首山下长约6.5 km和宽约500 m的范围内,已探明矿石储量5.2×108 t,镍金属储量5.5×106 t,列世界同类矿床第3位.金川铜镍矿床地质构造特征主要表现以下两个方面.
1) 金川矿区是一座典型的高地应力矿区,表现在矿体埋藏深,自重应力大,近似水平方向的构造应力最高达到50 MPa,即水平应力是垂直应力的1.69~2.27倍.
2) 金川矿床赋存于海西期含矿超基性岩体中,上盘围岩为二辉橄榄岩,下盘围岩主要为大理岩和二辉橄榄岩.矿区内断裂构造极其发育,F16、F15、F26等断层对矿岩条件产生剧烈影响,使矿岩异常破碎,表现出岩石强度高而岩体稳定性差的特征,由此给采矿方法选择和采场地压控制带来不利影响.
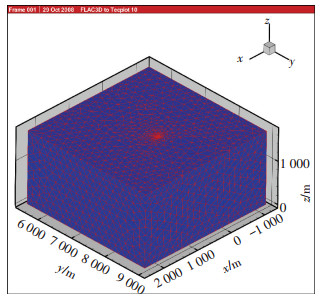
为优化采矿设计和实现对采场地压优化控制,金川镍矿开展了不同阶段的地应力测量,获得大量的地应力测量结果[24].根据金川龙首矿和二矿区地应力测量结果,建立包含两个矿区工程地质岩体的三维数值分析模型,进行金川矿区地应力场反演, 如图 1所示.
|
图 1 金川矿区地质体地应力场反演三维数值模型 |
根据金川矿区地应力测点位置、埋深、岩性以及地应力测量结果[24],选择表 1中9个地应力测试数据,用于金川矿区地应力反演.其中前5个数据用于建立优化模型,后4个数据用于检验地应力场反演结果.
| 表 1 金川矿区地应力测点位置和实测地应力值 |
为了建立金川矿区地应力影响函数,首先建立金川矿区工程地质体三维数值模型.三维数值模型坐标系统为:水平面指向东为x坐标,指向北为y坐标,垂直向上为z坐标(见图 1).
2.2.2 工程地质体分区与岩体参数选择考虑到矿岩体物理力学性质存在显著差异,根据力学特性划分成矿体和岩体两个分区,分别采用γ1,E1,μ1和γ2,E2,μ2表示矿岩体密度、弹性模量和泊松比.根据金川矿区已开展工程地质研究,确定矿岩体密度分别为2.8~3.6 t/m3和2.4~2.8 t/m3.矿岩体弹性模量分别为20~34 GPa和6~20 GPa;矿岩体泊松比分别为0.20~0.24和0.20~0.26.根据金川矿区地应力实测结果,确定金川矿区x、y水平方向的侧压系数分别为0.5~1.2和1.1~1.5.
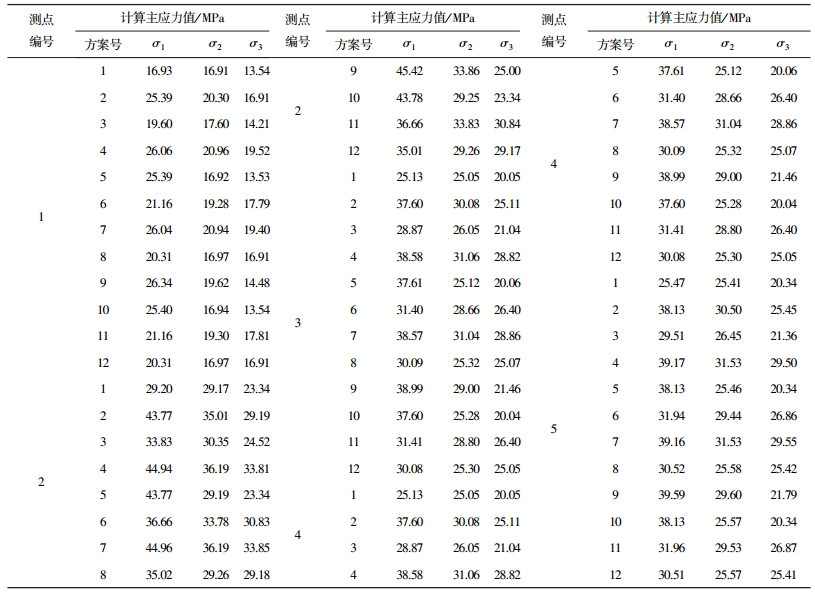
2.2.3 地应力影响因素和试验水平及正交数值分析选择矿体和岩体参数γ1,E1,μ1,γ2,E2,μ2和矿区侧压系数λ1、λ2共8个因素和两个水平进行金川矿区地应力场反演.表 2给出了8因素2水平地应力场反演三维正交数值分析的因素与水平,表 3给出了金川矿区地应力场反演三维正交数值分析的计算方案.
| 表 2 金川矿区地应力反演的三维正交数值分析因素和水平 |
| 表 3 金川矿区地应力反演的三维正交数值分析计算方案 |
根据图 1所示的金川矿区三维数值分析模型和表 3的正交数值计算方案进行12次数值分析.在每次计算结果中提取三维数值分析模型的地应力测点处的地应力计算值,由此获得如表 4所示的矿区地应力各测点处的3个主应力大小和主应力方向.
| 表 4 金川矿区地应力测点处的地应力数值计算结果 |
根据表 3正交数值计算方案和表 4地应力测点对应的地应力计算结果,采用遗传规划建立第j个地应力测点(j=1, 5)地应力与原岩参数(密度γ、弹性模量E、泊松比μ)及侧压系数λ1和λ2之间的函数关系为σ′ji=fij(γ1, E1, μ1, γ2, E2, μ2λ1, λ2), 其中,σ′ji(i=1, 3)分别为三维数值模型中第j个地应力测点的第i主应力的计算值;fij(i=1, 3;j=1, 3)分别为三维模型中第j个地应力测点的主应力与岩体参数和侧压系数的函数.
由于地应力函数具有高度非线性,因此采用遗传规划中的最佳遗传树表征,由此获得5个地应力测点处的3个主应力的函数表达式.本文仅给出图 2所示的测点1处的第1主应力σ11的最佳遗传树结构图,该点的地应力函数表达式为

|
(3) |

|
图 2 金川矿区地应力测点1位置的σ1的最佳遗传树 |
式中:xi(i=1, 8)分别为矿体参数γ1, E1, μ1、岩体系数γ2, E2, μ2和侧压系数λ1, λ2.
2.3 金川矿区地应力场智能反演优化模型基于金川矿区地质体中5个地应力测点处的地应力函数与实测地应力值之差的平方和最小为优化目标,由此建立矿区地应力场反演优化模型.
2.3.1 金川矿区地应力场反演目标函数根据金川矿区地应力的遗传规划函数关系,建立地应力场智能反演目标函数为
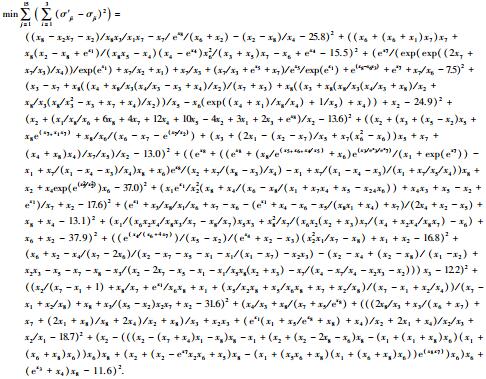
|
(4) |
根据金川矿区矿体和岩体参数以及地应力的变化范围,由此确定优化模型的约束条件为:
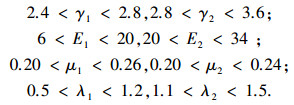
|
利用遗传算法的全局搜索能力,求解由目标函数式(3)和约束条件式(4)确定的地应力反演优化模型.首先设置遗传算法的参数见表 5;然后进行遗传算法操作:即随机产生初始群体→个体适应度评价→选择操作→交叉操作→变异操作→终止法则(最大遗传代数);最后获得与矿区地质体初始应力场相匹配的矿、岩体参数和矿区侧压系数见表 6.
| 表 5 遗传算法参数表 |
| 表 6 金川矿区矿、岩体参数和侧压系数反演结果 |
将地应力场反演获得金川矿区矿、岩体参数γ1*、E1*、μ1*,γ2*、E2*、μ2*和矿区的侧压系数λ1*、λ2*代入已经建立的金川矿区三维数值分析模型进行正分析,由此获得的应力场即为金川矿区工程地质体的原岩应力场.
3 金川矿区地应力场反演结果误差分析为检验地应力场反演结果的可靠性,表 7给出金川矿区4个测点的地应力实测值与反演值和误差分析结果.图 3显示了金川矿区6~9号测点的实测地应力值与反演地应力值的对比曲线.由此可见,采用本文的地应力反演方法获得的3个主应力值与实测主应力值的误差最大为17.98%,最小为0.62%.可见该地应力场反演方法具有一定的可靠性.
| 表 7 金川矿区4个点实测地应力值与反演地应力值的对比分析 |
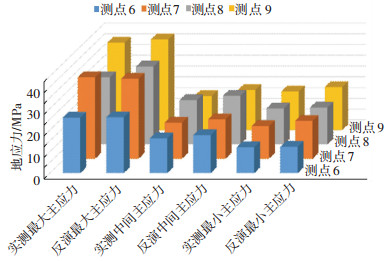
|
图 3 金川矿区4个测点实测地应力值与反演地应力值对比结果 |
1) 地质体中的原岩应力是时间和空间的函数,是岩体物理力学参数的高度非线性函数,因此,采用遗传规划的遗传树结构,能够表征地应力的非线性关系;考虑到地应力反演的优化目标函数属于高度非线性函数,利用遗传算法的快速寻优技术,能够获得目标函数的最优解.
2) 采用本文地应力反演方法,进行4个测点的主应力反演,并将反演结果与实测值对比,其最大误差为17.98%,最小误差为0.62%.考虑到地应力复杂特征及地应力测量存在的误差,地应力反演误差满足地质工程分析的精度,该方法可为复杂地应力场反演和工程稳定性分析提供一条途径.
| [1] |
司光晔, 张严. 基于地应力测试的公路岩爆预测技术研究[J]. 公路, 2013(6): 256-261. |
| [2] |
周垂一, 李军, 严鹏. 锦屏二级水电站深埋隧洞施工难点解析[J]. 隧道建设, 2013, 33(6): 481-488. |
| [3] |
马行东. 某电站枢纽区地下洞室岩爆的特征与预防措施[J]. 水电站设计, 2013, 29(1): 63-65. |
| [4] |
刘月锋, 卫栓紧. 深部开拓巷道岩爆防治技术[J]. 建井技术, 2013, 34(2): 13-15. |
| [5] |
杨旭旭, 靖洪文, 陈坤福, 等. 深部原岩应力对巷道围岩破裂范围的影响规律研究[J]. 采矿与安全工程学报, 2013, 30(4): 495-500. |
| [6] |
廖椿庭, 施兆贤. 金川矿区原岩应力实测及在矿山设计中的应用[J]. 岩石力学与工程学报, 1983, 2(1): 103-112. |
| [7] |
蔡美峰, 乔兰, 于波, 等. 金川二矿区深部地应力测量及其分布规律研究[J]. 岩石力学与工程学报, 1999, 18(4): 414-418. |
| [8] |
蔡美峰, 刘卫东, 李远. 玲珑金矿深部地应力测量及矿区地应力场分布规律[J]. 岩石力学与工程学报, 2010, 29(2): 227-233. |
| [9] |
康红普, 林健, 张晓, 等. 潞安矿区井下地应力测量及分布规律研究[J]. 岩土力学, 2010, 31(3): 827-831. |
| [10] |
罗超文, 李海波, 刘亚群. 深埋巷道地应力测量及围岩应力分布特征研究[J]. 岩石力学与工程学报, 2010, 29(7): 1418-1423. |
| [11] |
丰成君, 陈群策, 谭成轩, 等. 广东核电站地应力测量及其应用[J]. 岩土力学, 2013, 34(6): 1745-1752. |
| [12] |
李云鹏, 王芝银. 粘弹性位移反分析的边界元法[J]. 西安矿业学院学报, 1989(1): 17-23. |
| [13] |
郭锋, 马震岳, 金长宇. 抽水蓄能电站地下洞室初始地应力场反演分析-基于神经网络和快速拉格朗日算法[J]. 地下空间与工程学报, 2007, 3(2): 208-212. |
| [14] |
贾善坡, 陈卫忠, 谭贤君, 等. 大岗山水电站地下厂房区初始地应力场Nelder-Mead优化反演研究[J]. 岩土力学, 2008, 29(9): 2341-2349. |
| [15] |
岳晓蕾, 李术才, 陈启辉, 等. 多元多方程地应力反演与工程应用研究[J]. 山东大学学报:工学版, 2010, 40(2): 66-70. |
| [16] |
张国强, 王桂萱. 基于神经网络结构分解与FLAC3D的初始地应力场反演[J]. 大连大学学报, 2007, 28(6): 43-47. |
| [17] |
杨志双, 潘懋. 基于遗传算法(GA)的地应力有限元反演研究[J]. 水文地质工程地质, 2006, 33(2): 80-83. |
| [18] |
王福玉, 高谦, 张周平. 金川矿区地应力规律与人工神经网络预测研究[J]. 岩石力学与工程学报, 2003, 22(S2): 2601-2606. |
| [19] |
罗润林, 阮怀宁, 黄亚哲, 等. 岩体初始地应力场的粒子群优化反演及在FLAC3D中的实现[J]. 长江科学院院报, 2008, 25(4): 73-76. |
| [20] |
张贵庆. 三峡地下厂房区地应力场反演分析[J]. 水利与建筑工程学报, 2011, 9(4): 66-71. |
| [21] |
张延新, 蔡美峰. 地应力场与地质构造运动关系研究[J]. 铜业工程, 2004(3): 7-9. |
| [22] |
江权, 冯夏庭, 徐鼎平, 等. 基于围岩片帮形迹宏观地应力估计方法探讨[J]. 岩土力学, 2011, 32(5): 1452-1459. |
| [23] |
张宜虎, 卢轶然, 周火明, 等. 围岩破坏特征与地应力方向关系研究[J]. 岩石力学与工程学报, 2010, 29(S2): 3526-3535. |
| [24] |
杨志强, 高谦, 王玉山, 等. 特大型镍矿工程地质与岩石力学[M]. 北京: 科学出版社, 2013.
|
 2016, Vol. 48
2016, Vol. 48