2. 哈尔滨工业大学 电子与信息工程学院 150001 哈尔滨
2. School of Electronics and Information Engineering, Harbin Institute of Technology, 150001 Harbin, China
近年来,步态识别已是图像处理领域一个热点研究方向,卡内基梅隆大学(Carnegie Mellon University, CMU)、麻省理工学院(MIT)、马里兰大学、英国的南安普顿大学为此做了众多贡献.中科院自动所是国内较早开始步态识别研究的研究单位之一, 并提出了一种基于身体结构和运动行为的步态识别算法[1].
在步态识别研究中轮廓是关键的信息之一,文献[2]提出一种基于轮廓分析的方法,利用轮廓线上的点到质心的距离作为特征, 该方法对外套等因素的影响比较敏感.文献[3]在文献[2]基础上做了进一步的提高,将轮廓线分为上、下、左、右4部分,将这4部分分别投影在一个边界框来构成4个距离向量,该方法所用数据库大多样本少,在累计匹配当中第1次的识别率不高.文献[4]运用几何学理论进行识别.文献[5]在文献[4]基础上通过改进,在同样的数据库上做了实验,该方法并没有与其他的方法进行对比.文献[6]采用帧插法将半个周期的长度限制在固定的长度,进而求出边界向量上每一个点在半个周期内的变化曲线作为步态特征.由于该方法没有考虑轮廓的预处理操作, 对轮廓不完整的序列的识别率不高.文献[7]结合了轮廓的时空相关特征和统计物理参数,弥补了文献[6]的轮廓不完整的影响.文献[8]考虑的是轮廓外观变化的影响.该文献引用仿射不变矩(affine moment invariants, AMI)并采用最近邻法来匹配识别.文献[9-10]提出了基于关键帧的识别方法,这类方法会丢失序列中其他帧的信息,造成识别率的降低.文献[11]通过分析人体运动的对称性,采用广义对称性算子对人体的轮廓图像和图像序列的光流信息分别进行对称映射从而获取步态特征.文献[12]在轮廓的基础上提取空间分量、时间分量和小波能量分量作为步态特征,用支持向量机(SVM)分类器识别.文献[13]利用轮廓的宽高比、面积、纵坐标变化、质心变化曲线作为特征,获得较高的识别率.文献[14]采用轮廓的步态能量图法进行步态识别.文献[15]提出的基于部分轮廓频域步态熵特征的识别算法,通过分析轮廓不同区域单独考虑的识别效果来定义有效部分,识别率有明显的提高.
在上述算法中,针对轮廓不完整或者只考虑关键帧的情况,如文献[15]考虑轮廓有效部分的情况,在提取特征的过程中,造成部分信息丢失从而导致识别率降低.在选取特征的过程中只考虑单一类型特征,如文献[14]只是考虑轮廓在步态周期范围内的动态特征,该选取方法是不够完善的.基于此,本文通过提取轮廓两个完整周期的较低维数的静态特征和动态特征,使得最终的特征更能反映不同个体之间的步态差异;同时动态特征也避免了轮廓不完整造成的影响.为进一步提高识别率,本文采用改进的K近邻法进行分类识别.实验验证了该算法的有效性.
1 算法总框架本文所提算法主要包括预处理、特征提取和分类识别3个模块,具体流程如图 1所示.
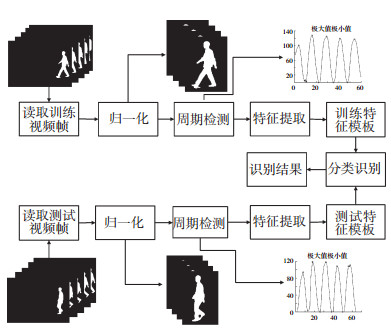
|
图 1 步态识别算法框图 |
为了便于后期特征提取,需将图像尺寸归一化.图 2为归一化尺寸的二值图像及边缘检测后的二值图像.根据步态序列轮廓面积变化求出每个步态样本的周期曲线,一个步态序列的周期曲线如图 3所示.图 3中空心圆代表极大值,即人在双腿着地分开最大时轮廓的面积,星号代表极小值,即双腿并拢时轮廓的面积.连续3个极大值之间的帧为一个步态周期.

|
图 2 归一化及轮廓 |
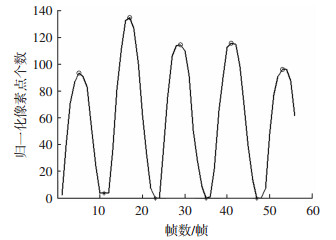
|
图 3 周期曲线 |
特征的获取应该既简单、有效,又能表示待识别的事物.首先,选取的角度距离特征作为本文步态特征的静态特征,该特征是从轮廓内考虑的帧内信息;其次,选取的不变矩特征是从轮廓形状的角度考虑,作为步态特征的第1个动态特征;最后,选取的帧差百分比特征,作为另一个动态特征,它是能够反映整个周期内轮廓的整体变化情况的,两个动态特征同时也是对角度距离特征的一个弥补.
3.1 角度距离特征提取文献[16]是将轮廓线上一定间隔内像素点个数作为特征,文献[17]是将轮廓线采样选取采样点到质心距离作为特征.对于轮廓不完整的步态序列,前者在表征步态时由于像素点缺失会有一定的误差,后者在步态轮廓线的手臂和腿部的采样点由于缺失而使特征曲线震荡.本文在选取特征时,与前两者的特征是不同的物理量,通过一定的改进,将两者结合起来,既合理利用了一定角度下轮廓点的坐标值,又更加准确的表征了轮廓线的整体特征,使得特征曲线平滑.具体提取特征方法如下.
1) 求取人体轮廓质心(Xc, Yc)为:
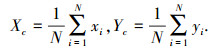
|
(1) |
式中:N为图像轮廓的像素点个数; xi为第i个像素的横坐标; yi为对应像素的纵坐标.
2) 求取轮廓线上点到质心方向与y坐标轴的夹角, 如

|
(2) |
3) 计算像素坐标到质心的距离disth.选取num个间隔,每个间隔为(360/num)°,根据式(2),再结合间隔大小求出轮廓上第H个间隔里所有像素的坐标到质心的距离disth;
4) 计算第H个间隔内所有距离的均值, 其表达式如

|
(3) |
式中ω为每个区间内不同的像素点数.如图 4(a)所示,两条线段所组成的区域为一个间隔.

|
图 4 角度距离特征曲线 |
图 4(b)为一个样本一个周期内某一帧轮廓的角度距离特征向量曲线.将一个半步态周期中提取出的归一化角度距离向量序列进行叠加求平均得到,最后的步态特征记作F1=[f1i1, f1i2, …, f1inum],i表示第i个样本序列,如图 4(c)所示.
3.2 图像不变矩特征提取文献[18]中提到图像的7个不变矩具有平移、旋转、比例不变性,在目标识别、图像匹配、形状分析等领域得到了广泛的应用.
对于任意非负整数p、q,二维图像模式f(x, y),在平面R2上的p+q阶矩定义为
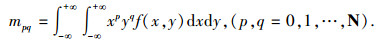
|
(4) |
式中:f(x, y)为图像的灰度(密度),仅在有限R2平面上分段连续; N为任意非负整数.显然,mpq由f(x, y)唯一确定,反之亦然.由于mpq不具有平移不变性,因此定义p+q阶中心矩为
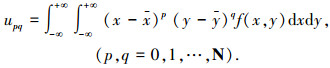
|
(5) |
式中:x=m10/m00, y =m01/m00为图像的质心.
归一化中心矩ηpq定义为:

|
(6) |
以下只列出前3个不变矩为
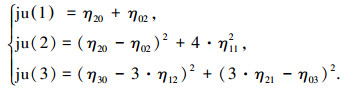
|
(7) |
在此将一定数目的图像进行叠加压缩为一帧图像,如图 5(a)~5(c)所示,分别为3个不同人的叠加图.求该帧图像的7个不变矩,则该图像不变矩特征可记作F3=[f3i1, f3i2, …, f3i7],i表示第i个样本序列.以此作为衡量人的轮廓在空间上的特征变化,从而区分不同的类.

|
图 5 不变矩特征 |
个体的步态很难从单个图片信息来确认个体之间的区别,步态本身是一种时空相关的运动,它的本质特征是人体的姿势随着时间的变化而发生的有序变化序列.对于熟悉的人往往通过其走路的姿势或者背影就能确定其身份,其中包含的有其平常走路的习惯速度和习惯姿势,因此容易判断.但对于不熟悉且走路相似的人之间的区别却难以判断,这就需要从细微的差别来区别个体,人体走路的加速度就能区分此细微差别.
加速度是描述物体速度变化快慢的物理量,也即单位时间内速度的改变量.文中考虑的是不同个体之间肢体运动的不同加速度,也即是人体抬脚走路的瞬间起步加速度的大小,加速度越大,帧间变化越明显,反之不明显.这样从视频帧的角度来看,相邻两帧之间在质心重合的情况下重合面积就不一样,也即是帧差百分比不同.因此,在一定程度上可以区别两个不同个体.为了提高识别率,将帧间的不同变化信息作为整个步态识别的运动信息,也避免了只考虑帧内信息的缺陷,因此,提出了帧差百分比的特征作为步态特征的一个动态特征.
设图像尺寸为M*L,每个样本每个不同序列所选的帧数为n,用Ti, j(m, l)表示一个人的第i个序列的第j帧轮廓图像对应位置(m, l)像素值,则
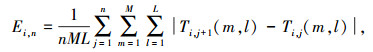
|
(8) |
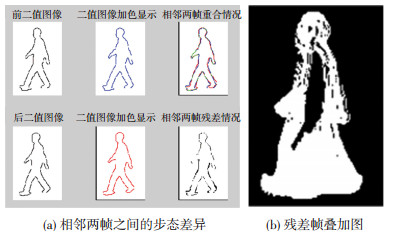
式中Ei, n为第i个样本序列的前n帧图像的残差百分比.为了便于分辨,加色显示,如图 6(a)所示,为相邻两帧之间的步态差异.最终残差帧在整幅图的百分比情况,如图 6(b)所示.该特征维数为1,记作F2.
|
图 6 帧差百分比特征 |
常用的相似性度量的方式有欧式距离、曼哈顿距离、切比雪夫距离、汉明距离、信息熵等.在此,选取欧式距离(euclidean distance)作为度量两个样本特征之间的相似性, 公式如
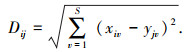
|
(9) |
式中:xiv为第i个样本特征的第v个分量; yjv为第j个样本特征的第v个分量; S为特征的维数; Dij为两个样本特征之间的相似度,其值越小,表示二者越相似.
4.2 分类识别通常所用的K近邻分类器(the K-nearest neighbor classifier,KNN)忽略了相似度值所属的权重大小,相当于将K个最近邻的值得权值平均化,使得在某些算法中的识别率不是太高.本文在相似性度量时将待测样本与训练样本之间欧式距离的权重问题考虑在内,采用加权机制,距离越近的权重越大,反之,越小.为此,提出了一种改进K近邻分类器(the modified K-nearest neighbor classifier)来对最终的特征进行分类识别.考虑到权重分配需要的是单调递减的函数.在此,选取反函数和指数函数的乘积作为权值函数,如
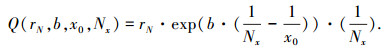
|
(10) |
式中:rN为权值归一化系数; b、x0分别为幅度调整参数; Nx为欧式距离从小到大排序所对应的序号.根据权值分配的原则,即距离最近的权值最大,反之越小,但是各个权值之间的偏差不能太大,本文选取标准偏差(standard deviation, SD)和平均绝对偏差(mean absolute deviation, MAD)两个指标来进行对权值的确定.其中一个较小的SD,代表大部分的数值和其平均值之间差异较小,而MAD由于差值被绝对值化,不会出现正负抵消的情况,因此也能更好的反映数值误差的实际情况.标准偏差(SD)和平均绝对偏差(MAD)定义为:

|
(11) |
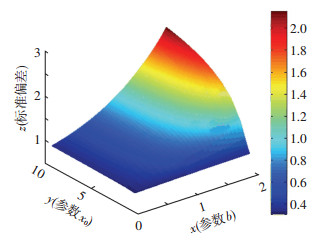
式中:Nxi为对应权值; Nq为权值的个数.通过构造以上两个指标与b、x0两个不同参数的函数关系,得出两个指标的三维显示图如图 7,8所示.
|
图 7 标准偏差三维显示图 |

|
图 8 平均绝对偏差三维显示图 |
再求出两个指标最小值所对应的参数值,即为本文选定的参数.由图可知b=1,x0=1.图 9为所选参数对应的归一化权值针状图.

|
图 9 权值针状图 |
本文实验是基于PC机Matlab7.12.0平台完成的.采用中科院自动化所公开的大型步态数据库CASIA-B[14]和卡内基梅隆大学提供的CMU Mobo步态数据库[19]进行实验.CASIA-B数据库包含124人(男93人,女31人),每人11个视角,每个视角下有3种行走状态(普通条件、穿大衣、携带包裹条件).其中,正常状态下有6个序列,其他各两个序列.图片尺寸大小为320×240,帧速率为25帧/s.CMU Mobo步态数据库在室内跑步机上采集,共25人(男23人,女2人),每人6个视角,每个视角下有4种行走步态(慢走、快走、跑步机倾斜一定角度慢走、双手拿球慢走),每人在每个状态下记录11 s,图片尺寸为468×640,帧速率为30帧/s.图 10为CMU Mobo步态数据库中3个样本图片.本文实验图片统一归一化尺寸为165×110.

|
图 10 CMU Mobo步态数据库样本 |
在实验过程中,将CASIA-B数据库中每个样本90°视角的6个正常行走序列,分别选取其中3个序列作为训练序列,剩余3个作为识别序列,分别进行以上所有处理,获得最终的训练特征和测试特征,分别输入不同的分类器进行识别,进行10次实验,结果见表 1.表 2是本文算法与文献中算法在CASIA-B数据库上的对比.为证明本文算法在不同数据库上的识别效果,在CMU Mobo步态数据上同样选取侧面视角的3种步态(慢走、快走、双手拿球慢走)进行了实验.
| 表 1 不同特征不同分类器的识别结果 |
| 表 2 4种识别算法在CASIA-B上的识别率比较 |
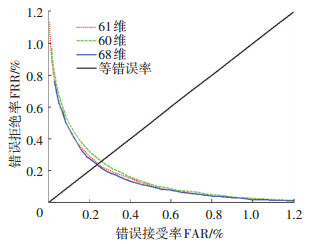
表 1选取CASIA-B数据库中全部样本,采用单一角度距离特征、静态角度距离特征和帧差百分比特征两者结合、静态角度距离特征和帧差百分比特征以及不变矩特征三者结合的方法,分别用KNN和改进KNN分别进行分类识别.表 1中KNN法最高识别率为93.55%,改进KNN法最高识别率为99.19%.单一特征维数为60维,KNN法最高识别率为91.94%,改进KNN法最高识别率为96.77%,提高接近5个百分点.两种特征结合后特征维数为61维,KNN法最高识别率为92.74%,改进KNN法最高识别率为98.39%.3种特征结合后维数为68维,KNN法最高识别率为93.55%,改进KNN法最高识别率为99.19%.显然对于KNN法在特征维数增加的情况下,识别率的提高没有改进KNN法好.从特征上看,通过增加特征,在采用同一分类器的基础上,识别率相对于单个特征都有所提高;从分类器上看,两种分类器无论是单个特征还是多个特征,都是改进KNN法识别率最高,而且特征维数越高,识别率越高.为了进一步表明算法识别效果,通过增加不同特征维数对应的ROC曲线来说明算法的有效性.如图 11所示,横坐标是错误接受率FAR(false acceptance rate),纵坐标是错误拒绝率FRR(false reject rate).由图 11可知,3种特征维数下,曲线都很接近坐标轴,等错误率都在0.25%之下.
|
图 11 ROC曲线 |
表 2中文献[13]是将时空运动特征和轮廓的物理参数结合的并通过确定性学习理论的识别算法,采用SVM分类器和最小错误准则进行分类,识别率为98.40%.文献[14]是采用基于轮廓的步态能量图法,并用最近邻分类器进行分类识别,在CASIA-B数据库中90°视角的正常步态实验识别率为97.60%.文献[15]采用频域步态能量熵的基于轮廓有效部分的识别算法,将有效部分之间的欧式距离作为相似性度量的标准进行分类,识别率为98.56%.通过对比可知,本文算法对步态识别效果有一定的提高.本文算法和表 2中其他3种算法都是在统一的步态数据库上进行实验,该数据库采集的步态序列的背景是比较单一的,在此条件下,其他3种算法识别率已很高,而本文算法识别率在此基础上有一定的提高,在实际复杂背景的环境中,同样会有提高,证明该算法有一定实用价值.另外,在CMU Mobo步态数据库上也采用本文算法进行实验,尽管该数据库提供的前景背景分割图片有很大的噪声,但并没有影响本文算法识别效果,表明该算法具有较好的鲁棒性.
6 结论1) 本文提出一种有效的步态识别算法,结合前人研究的基础上,将两种方法进行结合,提出一种改进的角度距离特征,作为步态序列图象的静态特征进行步态识别.
2) 为更加准确的表征步态,提取了帧差百分比特征作为步态序列的动态特征进行步态识别.在增加维数不多的动态特征以后,识别率有了明显提高.
3)为了进一步提高识别率,在分类识别的过程中,提出一种改进的K近邻法,采用中科院自动化所提供的CASIA数据库和卡内基梅隆大学提供的CMU Mobo步态数据库进行的相关实验,证明了算法的有效性.
| [1] |
中科院自动化所生物特征认证与测评中心. 新兴的步态识别技术[J]. 中国安防, 2003(6): 43-43. |
| [2] |
WANG Liang, TAN Tieniu, NING Huazhong, et al. Silhouette analysis-based gait recognition for human identification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1505-1518. DOI:10.1109/TPAMI.2003.1251144 |
| [3] |
EKINCI M. A new approach for human identification using gait recognition[J]. ICCSA, 2006, 1216-1225. |
| [4] |
SINGH J P, AGRAWAL S. An approach for human gait identification based on area[J]. IOSR Journal of Computer Engineering, 2013, 10(3): 43-47. DOI:10.9790/0661 |
| [5] |
GANGOTIA P, SHRIVASTAVA G S, SINGH J P. An approach of human identification based on gait[J]. International Journal of Computer Applications, 2014, 93(1): 33-36. DOI:10.5120/16182-5404 |
| [6] |
LEE C P, TAN A W C, TAN S C. Gait recognition via optimally interpolated deformable contours[J]. Pattern Recognition Letters, 2013, 34(6): 663-669. DOI:10.1016/j.patrec.2013.01.013 |
| [7] |
CHOUDHURY S D, TJAHJADI T. Silhouette-based gait recognition using procrustes shape analysis and elliptic fourier descriptors[J]. Pattern Recognition, 2012, 45(9): 3414-3426. DOI:10.1016/j.patcog.2012.02.032 |
| [8] |
IWASHITA Y, UCHINO K, KURAZUME R. Gait-based person identification robust to changes in appearance[J]. Sensors(Basel), INNS, 2013, 13(6): 7884-7901. |
| [9] |
ZHAO Guoying, CHEN Rui, LIU Guoyi, et al. Amplitude spectrum-based gait recognition[C]//Proceedings of the 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition. Seoul, South Korea: IEEE Computer Society, 2004: 23-28. doi: http://doi.ieeecomputersociety.org/10.1109/AFGR.2004.1301504.
|
| [10] |
COLLINS R T, GROSS R, SHI Jianbo. Silhouette-based Human identification from body shape and gait[C]//Proceedings of the fifth IEEE International Conference on Automatic Face and Gesture Recognition. Washington, DC: IEEE Computer Society, 2002: 351-356.
|
| [11] |
HAYFRON-ACQUAH J B, NIXON M S, CATER J N. Automatic gait recognition by symmetry analysis[J]. Pattern Recognition Letters, 2003, 24(13): 2175-2183. DOI:10.1016/S0167-8655(03)00086-2 |
| [12] |
SUDHA L R, BHAVANI R. Biometric authorization system using gait biometry[J]. International Journal of Computer Science, Engineering and Applications, 2011, 1(4): 1-13. DOI:10.5121/ijcsea.2011.1401 |
| [13] |
ZENG Wei, WANG Cong, YANG Feifei. Silhouette-based gait recognition via deterministic learning[J]. Pattern Recognition, 2014, 47(11): 3568-3584. DOI:10.1016/j.patcog.2014.04.014 |
| [14] |
YU Shiqi, TAN Daoliang, TAN Tieniu. A framework for evaluating the effect of view angle, clothing and carrying condition on gait recognition[C]//Proceedings of the 18th International Conference on Pattern Recognition. Washington, DC: IEEE, 2006: 441-444. doi: 10.1109/ICPR.2006.67.
|
| [15] |
ROKANUJJAMAN M, ISLAM M S, HOSSIAN M A, et al. Effective part-based gait identification using frequency-domain gait entropy features[J]. Multimedia Tools and Applications, 2015, 74(9): 3099-3120. DOI:10.1007/s11042-013-1770-8 |
| [16] |
王亮, 胡卫明, 谭铁牛. 基于步态的身份识别[J]. 计算机学报, 2003, 26(3): 353-360. |
| [17] |
赵子健, 吴晓娟, 刘允才. 基于角度直方图的步态识别算法[J]. 计算机工程与科学, 2006, 28(6): 73-76. |
| [18] |
BRGERON B P. Bioinformatics computing[M]. Indianapo-lis, USA: Prentice Hall PTR, 2002.
|
| [19] |
GROSS R, SHI J. The CMU motion of body (mobo) da-tabase[R]. technical report. Robotic Institute, Carnegie Mellon University, Pittsburgh, PA, CMU-RITR-01-18, 2001.
|
 2016, Vol. 48
2016, Vol. 48




