2. 哈尔滨学院 工学院, 150086 哈尔滨
2. Engineering Institute, Harbin University, 150086 Harbin, China
图像分割是把图像分成多个具有显著界限(轮廓/边界)区域的处理过程.所有的图像分割方法可以分为两大类:分析算法和统计算法.主动轮廓[1]和水平集方法[2]属于前者,它们基于给定图像的信息来获得区域的轮廓.基于统计的方法,如主动形状模型[3]和空间分割模型[4],则根据分析训练样本间相似性的变化来进行图像分割.但是统计方法因需要一定量的训练样本,且分析方法受到噪声或显著特征的干扰而使轮廓发散,所以在某些应用上是不适合的.本文将主要研究水平集方法的图像分割.
基于水平集方法的主动轮廓模型是近年来快速发展的一种图像分割方法,在图像处理和计算机视觉等领域得到了广泛的应用[2].基于水平集方法的主动轮廓模型与文献[1]提出的主动轮廓模型(也叫snake模型)的不同之处在于:基于水平集方法的主动轮廓模型将图像不同区域之间的边界作为零水平集嵌入定义在图像区域上的高一维的水平集函数中,并利用对整个水平集函数的演化代替传统的主动轮廓模型对图像不同区域间边界曲线的演化,最终通过演化得到一个定义在图像区域上的水平集函数,该水平集函数中的零水平集代表了图像不同区域间边界的位置.根据建立能量泛函的不同思想,基于水平集方法的主动轮廓模型可以分为两类:基于边缘的模型和基于区域的模型.基于边缘的模型对图像上的边缘信息(如图像的梯度)有较好的响应,而基于区域的模型通常可以更好地考虑图像不同区域中的整体信息(如区域中的平均灰度、整体纹理特征等).对于具有高噪声和低对比度,不同区域间边缘模糊不清的图像,基于边缘的模型通常不能取得很好的分割效果.而基于区域的模型可以对区域上整体信息进行建模,更有利于处理高噪声、低对比度、边缘不清等问题. CV模型[5]作为经典的主动轮廓模型,它的能量泛函是基于区域信息的,该方法在被分割图像存在弱边界的情况下也能检测到对象的内部轮廓.但是该方法只适用于均匀图像的分割处理,对亮度不均匀图像的处理效果不是很好,特别是文献[6-7]中提到的分段图像(PS),它们都具有较高的计算复杂度且对初始轮廓比较敏感.针对这个问题,先后出现了RSF模型[8]、LCV模型[9]、LIF模型[10]和其他的方法[11-16],它们都针对分割能量函数进行了修正,与CV法相比,这些模型在分割效率和有效性方面都得到了增强. RSF模型中因能量函数中所用能量为局部拟合能量,使得其能量函数存在许多局部最优解.文献[17]对RSF模型进行改进,引入局部有序能量,提出了一个Order-LBF的图像分割模型, 通过添加局部灰度约束即局部有序能量减少局部最优解的数目,从而能够得到比RSF模型更稳定和理想的分割效果.
本文在RSF模型的基础上进行能量泛函的改进,将Kullback-Leibler散度加入到RSF模型中,形成一个新的能量泛函模型(KL-RSF模型).实验结果表明,加入类间距信息的KL-RSF模型与RSF模型、LCV模型、LIF模型、LBF+Order相比,具有较低的计算量和很好的分割性能和效率.
1 RSF模型在RSF模型的能量函数中,x是灰度图像Ω中的一个点,x∈Ω,I: Ω⊂R2→R,C是图像Ω中的一个闭合曲线,它将图像Ω分为两个适应子区域Ω1和Ω2,f1(x)和f2(x)分别为这两个区域中以x为中心点的小区域内亮度的近似值. RSF模型中拟合能量的定义为

|
(1) |
其中λ1和λ2是两个正常数,代表权重参数,Kσ(x-y)是一个尺度参数σ>0的核函数. RSF模型的拟合能量模型的物理意义如图 1所示.在子区域Ωi中,y是以点x为中心, 半径为σ的圆形邻域内的一点. EFit的最小值能够引导曲线C去发现目标边缘,拟合函数fi(x)是曲线C两边区域的局部图像亮度的最佳逼近值.
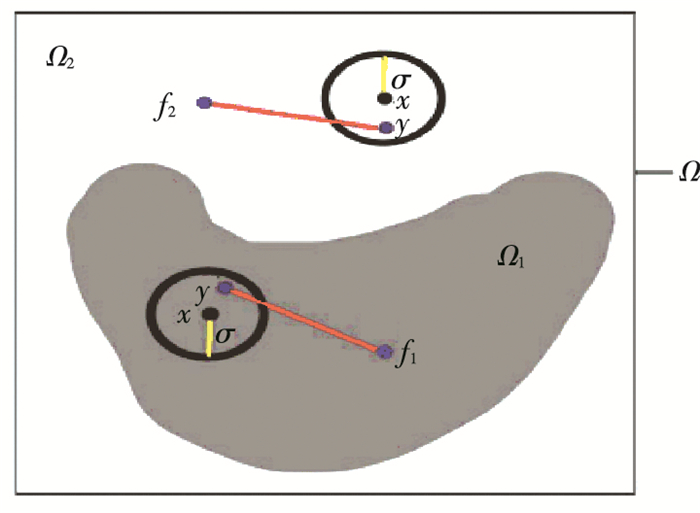
|
图 1 RSF模型拟合能量模型的示意 |
在演变过程中为了平滑曲线C,把正规项(曲线的长度|C|)引入到函数中,修改后的能量函数可改写为

|
(2) |
为了处理拓扑变化,一般要把能量函数ERSF代入到一个变分水平集,并通过梯度下降法来计算.水平集函数φ从轮廓C的内部区域Ω1到外部区域Ω2的定义为
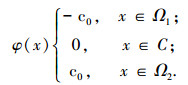
|
其中C∈Ω是一个用零水平集函数表示的轮廓.
文献[8]中RSF模型能量泛函的水平集格式为
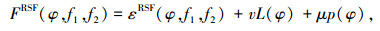
|
(3) |
其中前两项εRSF(φ, f1, f2)和L(φ)分别是数据拟合项和长度项,对应式(2)中右端的两项.最后一项是新加入的水平集正则项,该项可以保证分割结果的准确性,水平集演化的稳定性,以及避免重新初始化水平集函数.它们的表达式为

|
其中M1(φ)=H(φ), M2(φ)=1-H(φ).为了极小化能量函数式(3), 本文同样使用光滑的Heaviside函数Hε(x)来近似H(x),Hε(x)和δε(x)分别是Heaviside函数和Dirac函数的正规化函数[9], 而且δε(x)是Hε(x)的导数.它们的表达式如式(4)所示,拟合能量fi(x)的表达式如式(5)所示:

|
(4) |
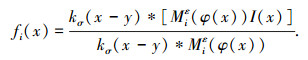
|
(5) |
从文献[8]可知,RSF模型可以很好地对不均匀图像进行分割,然而在等式(5)中,卷积运算是非常耗时的,所以本文对RSF模型进行了改进,提出了加入KL散度的改进RSF模型来有效地解决这一问题.
2.1 模型的能量函数基于几何主动轮廓模型的图像分割可以被看作是一个聚类问题,现存的方法通过最小化图像中每个点的灰度与其所在区域灰度的“拟合中心点”的距离来寻找目标的轮廓[18-19].图像中各区域可以看作不同类别,而区域的“拟合中心点”代表该类别,与区域“拟合中心点”距离小的就认为其归属于该类.为了使主动轮廓能准确地发现亮度不均匀图像中的目标边界,RSF模型使用局部能量拟合项来确保同质区域内的像素具有相似特征,即像素是否属于该区域是由最小化该项来决定的,即使聚类中的类内距离最小.
在保证分割结果准确的前提条件下,为了使轮廓演化速度更快,把类间信息,即区域间(轮廓内部和外部)的统计差异,加入到RSF的能量函数中.通过最大化类间距离来使分割变得更快和更容易.任意两个区域的KL散度指出了它们之间的相似性,数值越高意味着两个区域越不相似,从而使分割的速度越快.通过引入区域间的KL散度能量,可以令区域间的KL散度能量最大化,即最大化两个区域之间的差异,使距离区域“拟合中心点”较远的边缘点不因为式(1)中拟合能量的最小化,而被划分到错误的区域中,从而使分割的结果更准确.另外,随着区域间差异的增加,也使得各点划分到其所属区域中的过程加快,能量函数最小化的求解收敛速度增加,即加快了图像分割的速度.改进后能量函数的定义为

|
(6) |
其中γ1和γ2是用于平衡两个能量项性能的系数.
图 2(a)显示了RSF方法的能量函数,图 2(b)显示了本文方法的能量函数. 图 2中的黑线表示了式(6)中的第一项EFit,两个点C1和C2分别表示区域Ω1和Ω2的亮度“中心”.拟合函数是两类距离的和:一类距离是区域Ω1内的点到亮度“中心”C1的距离,另一类距离是区域Ω2内的点到亮度“中心”C2的距离.可通过最小化相同区域内黑色线的长度来得到目标边界. 图 2 (b)中显示的虚线距离和表示了式(6)中的第二项EKL.每一条虚线表示区域Ω1 (或Ω2)内的点到另外一个区域亮度“中心” C2 (或C1)的距离.因为EKL值越大意味着两个区域相似性越小,所以最大化EKL将使某区域内的点与其它区域的点产生更大的差异,进而加速分割的处理过程. 图 2(b)给出了包含类内距离的能量项EFit (图中黑线)和包含类间距离的能量项EKL (图中虚线)的示意图,本文将这两种距离结合到一起来进行图像分割,称为KL-RSF模型.
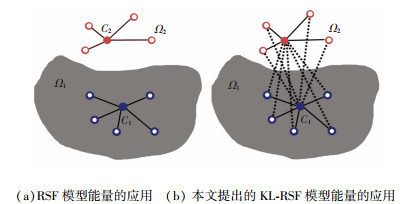
|
图 2 现有RSF模型与本文提出的KL-RSF模型能量的比较 |
用于构建的能量项EKL的KL散度表达式为

|
(7) |
其中p和q表示两个概率分布.根据文献[20]对KL散度的描述,能量EKL的定义为
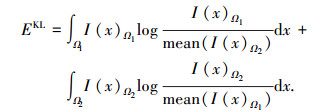
|
其中I(x)Ω1和I(x)Ω2分别表示区域Ω1和Ω2内像素点的亮度.从式(7)可以看出,如果I(x)Ω1 (或I(x)Ω2)逼近I(x)Ω2 (或I(x)Ω1)的均值,意味着区域Ω1 (或Ω2)中点的亮度接近区域Ω2 (或Ω1)点的平均亮度,
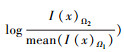
由于本文方法的分割是由最小化全局能量EFit和最大化第二项EKL来完成的,所以EKL前的系数γ2是负的,进而使整个能量函数最小.
2.2 水平集函数表达式为了清晰阐述模型的表达式,使用两段水平集来解决能量函数最小化问题.由于系数γ1的作用可以用系数λ1和λ2来表示,所以把正规项代入到水平集函数后,分割的整个能量函数可以表示为
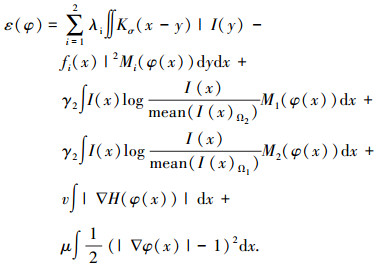
|
其中∫|∇H(φ(x))|dx是φ的零水平轮廓长度的正规项,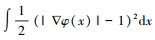
梯度下降法经常被用于水平集函数φ的能量函数最小化.即f1和f2被固定,通过标准梯度下降法来求解梯度流方程,进而使能量函数最小化.

|
其中:
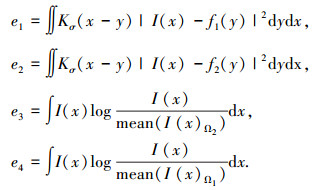
|
为了验证KL-RSF模型的准确性、鲁棒性等处理效果, 针对不同类型的图像进行处理,并把处理结果和其他方法进行比较.全部实验是在3.20 GHz CPU, 4GB RAM的惠普台式机上使用Matlib2011b完成的.实验中的参数如下:迭代的时间步长Δt=0.1,参数λ1、λ2和ν的值取1,长度约束项的系数μ的大小随分割图像的变化而改变.其中引入的能量EFit前的系数γ2的值,在用于合成图像和医学图像分割时,取值都为1,而在自然图像分割时其取值根据图像的不同进行调整.
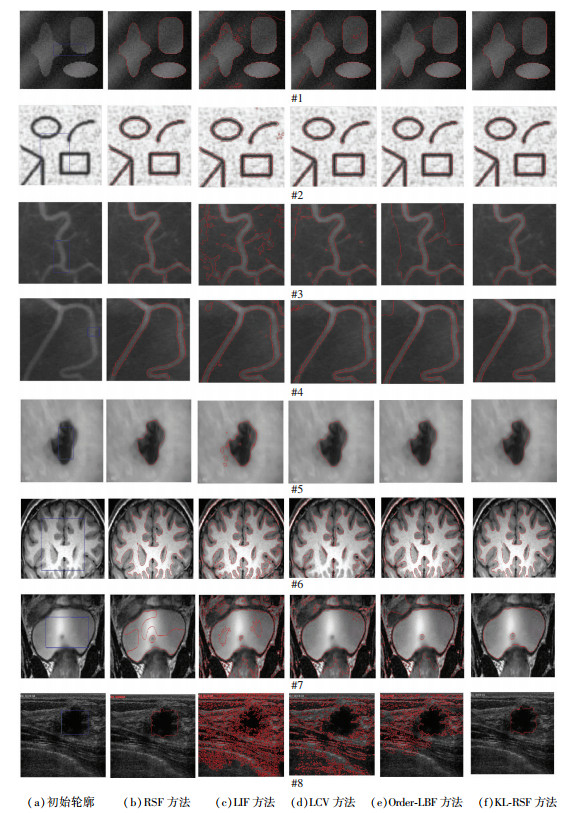
3.1 轮廓定位的准确性在本实验中,通过把KL-RSF模型分别应用到合成图像和真实医学图像来验证本文模型的效果,具体处理结果如图 3所示.在图 3中,第一列显示的是图像的初始轮廓,接下来的5列从左到右依次显示的是RSF模型、LIF模型、LCV模型、Order-LBF模型和本文模型的处理结果.从实验结果可以看到,LCV模型和LIF模型对图#2和图#5的分割效果较好,而RSF模型的分割效果与其相比有所提高,因其能量函数就是针对非均匀图像进行构造,只有对图#7和#8的分割结果不是很理想. Order-LBF模型虽然通过引入局部有序能量以减少局部最优解的数目,但仍陷入局部最优解,导致分割结果不理想.而本文的模型通过引入KL能量即全局信息,使求得的解为全局最优,实验结果也证明本文模型与其他模型相比具有更好的准确性,因其具备RSF模型分割非均匀图像的能力,同时又因为KL能量的引入,使最终求得的解全局最优.
|
图 3 本文模型和现存算法分割结果的比较 |
为了进一步证实本文方法的效果,把它应用到自然图像分割,在Berkeley分割数据集BSDS300上进行测试,并把处理结果同人工分割结果进行对比,比较结果如图 4所示.在图 4中从左到右分别表示原始图像、手工分割的结果、RSF模型的分割结果、LIF模型的分割结果、LCV模型的分割结果、Order-LBF模型的分割结果和本文模型的分割结果.通过对比,可以看出本文方法比其他4种方法更接近手工分割结果.其分割效果不理想的原因也是因为其他模型得到的解为局部解.

|
图 4 本文模型和现存算法在公共测试集上分割结果的比较 |
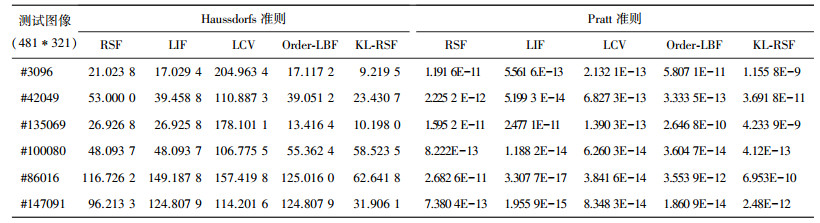
为了对KL-RSF模型进行客观评价,使用两个著名的评价准则:PRA距离[20]和Hausdorff距离[21]来进行评价.其中Hausdorff距离检测两幅图像的相似性,较低的值意味着较好的分割结果.计算图像间Hausdorff距离的公式为

|
其中: 
PRA经验测度是一个最常用的对两个像素组进行比较的措施, PRA的计算公式为
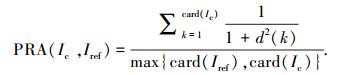
|
其中的d(k)是一个分割轮廓上Ic的第k个点到参考轮廓Iref最近点的距离. 表 1列出了RSF模型、LIF模型、LCV模型、Order-LBF模型和本文模型使用Hausdorff距离和PRA距离的定量对比结果.使用手工分割图像作为Iref,使用相应模型的分割结果作为Ic. Hausdorff距离越小,说明该模型的分割结果与手工分割结果越接近;相反,PRA距离越大,说明两种结果越接近. 表 1的实验结果显示,与其他模型相比较,本文的模型对除图#100080外的两个评价指标结果更优, 而RSF模型对图#100080的评价指标为最优.观察图 4中RSF模型的分割结果,可以看到其分割结果集中熊身体,而没有找到熊身体两侧草的轮廓,同时两侧草的轮廓存在于人工分割结果中,因此导致两个评价指标的计算结果较好.综合来看评价指标结果,本文模型的分割效果好于其他4种方法.
| 表 1 定量评价的结果 |
为了验证KL-RSF对噪声的鲁棒性,选择图 3中的#2图像作为测试图像, 这是因为#2图像中包含较多的目标.在图 5的第一行,可以看出图像从左到右分别被加入了不同程度的高斯噪声(μ=0,σ2=10, 15, 20, 25).在图 5的第二行到第六行分别显示了RSF模型、LIF模型、LCV模型、Order-LBF模型和本文模型的分割结果.从图 5中可以看出,本文模型引入的KL能量增强区域间的差异,从而能够准确处理噪声点,得到较好的分割结果.其他模型都是根据局部信息构造能量函数,导致噪声的出现严重影响其分割的准确性,从而得到的结果随着噪声的增强而变差.与其他模型相比,KL-RSF模型可以得到较好的分割结果,并且对噪声具有很好的鲁棒性.

|
图 5 对噪声图像分割结果的比较 |
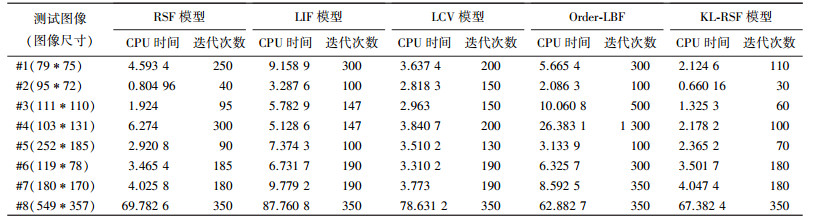
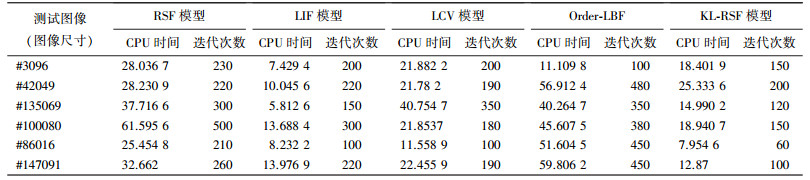
一个模型的效率可通过比较最终轮廓所需要的迭代次数和完成分割过程所用的CPU时间来进行验证.完成图 3和图 4分割过程所需要的迭代次数和CPU时间如表 2和表 3所示.由表 2可知,KL-RSF模型与其他4种方法相比只需要较少的迭代次数,LCV模型分割图#6和#7的CPU时间比KL-RSF模型少,其原因之一是其陷入局部最优解.此外,由于KL能量的引入,增加了单次迭代的计算时间. LCV模型虽然在分割图#6和#7时所用的分割时间减少,但分割结果较差.
| 表 2 图 3分割过程所需迭代次数和CPU时间的比较 |
| 表 3 图 4分割过程所需迭代次数和CPU时间的比较 |
从表 3中可知,对图像#42049进行处理时,LCV模型的迭代次数比KL-RSF模型要少,但是从图 4的处理结果可知,LCV模型在对该图像进行分割时的结果要比本文模型差,这是因为LCV模型很容易陷入到局部解,所以它只需要较少的迭代次数,但分割效果并不理想.此外,Order-LBF模型对图#3096分割的迭代次数也存在上述问题,从图 4可以看出,其只分割出飞机内部阴影区域,而没有找到飞机的整体轮廓,因此分割时的迭代次数相对较少.在CPU处理时间上,LIF模型分割4幅图像的时间少于其他模型,但从图 4的分割结果可以看到,LIF模型的分割结果较差,原因与对表 2的分析相同.
为了验证能量函数EKL的影响,对包含该项的KL-RSF模型和不包含该项的RSF模型的收敛演化过程进行了对比实验,对图 3中图像处理后的性能比较结果如图 6所示,横坐标是模型得到最终轮廓所需要的迭代次数,纵坐标是在不同迭代次数时的能量函数值,其中图中的小图是KL-RSF变化曲线的局部放大图.从图 6可以看到,RSF模型的演变不稳定,很容易陷入局部最优解,而KL-RSF模型的演变稳定, 可以快速得到最优解,这是由这两个模型能量函数的结构决定的.在RSF模型中只考虑了类内距离,而KL-RSF模型同时考虑了类内距离和类间距离,因此RSF模型的能量函数只利用图像的局部区域信息,而KL-RSF模型则能得到图像的全局信息, 进而使曲线的演变变快.

|
图 6 RSF模型和KL-RSF模型的收敛演变的比较 |
KL-RSF模型在RSF模型中加入由KL散度信息表示的类间距离能量项,提高了模型的运算速度,降低了模型的计算复杂度.通过对合成图像和实际图像的处理结果可知,KL-RSF模型与现有的RSF模型、LIF模型、LCV模型相比,具有更好的处理效果和计算效率,在保证分割结果的前提下使分割的收敛速度变得更快.
| [1] |
KASS K, WITKIN A, TERZOPOULOS D. Snakes:active contour models[J]. Int J Comput Vis, 1988, 1(4): 321-331. DOI:10.1007/BF00133570 |
| [2] |
OSHER S, SETHIAN J A. Fronts propagating with curvaturedependent speed:algorithms based on Hamilton-Jacobi formulations[J]. J Comput Phys, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [3] |
SHI D, GUNN S R, DAMPER R I. Handwritten Chinese radical recognition using nonlinear active shape models[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 2003, 25(2): 277-280. DOI:10.1109/TPAMI.2003.1177158 |
| [4] |
LIU G, LIN Z, YAN S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184. DOI:10.1109/TPAMI.2012.88 |
| [5] |
ZHOU Min. Mather theory for piecewise smooth lagrangian systems[J]. Science China(Mathematics), 2014, 57(5): 1033-1044. |
| [6] |
VESE L, CHAN T. A multiphase level set framework for image segmentation using Mumford and Shah model[J]. Int. J. Computer Vision, 2002, 50(3): 271-293. |
| [7] |
TSAI A, YEZZI A, WILLSKY A S. Curve evolution implementation of the Mumford-Shah functional for image segmentation, denoising, interpolation, and magnification[J]. IEEE Trans Image Process, 2001, 10(8): 1169-1186. DOI:10.1109/83.935033 |
| [8] |
LI C, KAO C, GORE J, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Trans. Image Process, 2008, 17(10): 1940-1949. DOI:10.1109/TIP.2008.2002304 |
| [9] |
WANG X, HUANG D, XU H. An efficient local Chan-Vese model for image segmentation[J]. Pattern Recognition, 2010, 43(3): 603-618. DOI:10.1016/j.patcog.2009.08.002 |
| [10] |
ZHANG K, SONG H, ZHANG L. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 43(4): 1199-1206. DOI:10.1016/j.patcog.2009.10.010 |
| [11] |
CHEN Jinhui, YANG Jian. Robust subspace segmentation via low-rank representation[J]. IEEE Trans on Cybernetics, 2014, 44(8): 1432-1445. DOI:10.1109/TCYB.2013.2286106 |
| [12] |
WANG Y, XIANG S, PAN C, et al. Level set evolution with locally linear classification for image segmentation[J]. Pattern Recognition, 2013, 46(6): 1734-1746. DOI:10.1016/j.patcog.2012.12.006 |
| [13] |
WANG L, SHI F, LI G, et al. Segmentation of neonatal brain MR images using patch-driven level sets[J]. NeuroImage, 2014, 84(1): 141-158. |
| [14] |
Song T, Yu L, Yi S. Ratio-and distribution-metric-based active contours for SAR image segmentation[C]//Fifth International Conference on Intelligent Control and Information Processing. Dalian: IEEE, 2014: 227-232.
|
| [15] |
LI C, HUANG R, DING Z, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Trans. Image Process, 2001, 20(7): 2007-2016. |
| [16] |
ZHANG K H, SONG H, ZHANG L. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 43(4): 1199-1206. DOI:10.1016/j.patcog.2009.10.010 |
| [17] |
WANG L, YU Z, PAN C. Medical image segmentation based on novel local order energy[C]//Asian Conferenceon Computer Vision. Queenstown: Springer, 2010: 148-159.
|
| [18] |
BALLA-ARABE S, GAO X, WANG B. A fast and robust level set method for image segmentation using fuzzy clustering and Lattice Boltzmann method[J]. IEEE Trans. System, Man, and Cybernetics-part B:Cybernetics, 2013, 43(3): 910-920. |
| [19] |
WANG L, PAN C. Robust level set image segmentation via a local correntropy-based K-means clustering[J]. Pattern Recognition, 2014, 47(5): 1917-1925. DOI:10.1016/j.patcog.2013.11.014 |
| [20] |
PRATT W K, FAUGERAS O D, GAGALOWICZ A. Visual discrimination of stochastic texture fields[J]. IEEE Trans. Systems, Man, and Cybernetics, 1978, 8(11): 796-804. DOI:10.1109/TSMC.1978.4309867 |
| [21] |
BEAUCHEMIN M, THOMSON K, EDWARDS G. On the Hausdorff distance used for the evaluation of segmentation results[J]. Can. J. Remote Sens., 1998, 24(1): 3-8. DOI:10.1080/07038992.1998.10874685 |
 2016, Vol. 48
2016, Vol. 48