通信系统中的成型滤波器常用来滤除基带信号频谱中的高频分量,消除码间干扰[1-2].由于FIR滤波器可以实现严格的线性相位,减少失真,因此在实现方式上,成型滤波器设计主要采用FIR滤波器实现.在时域上,滤波器的实现是将输入信号和滤波器的抽头系数进行卷积运算,实现结构包括3个基本单元:抽头延迟线、乘法器和加法器.由于加法运算相对较快,乘法运算的速度往往影响或决定了整个系统的速度.所以如果可以实现快速乘法,则整个系统的处理速度可以大大提高[3].
分布式结构DA(distributed architecture)是一种重要的硬件实现技术,它巧妙地利用ROM查找表,将固定系数的乘累加运算转换成查找表操作,从而避免了乘法运算.同时,查找表后的数据执行的都是简单的加法运算,因此可以很大程度地提高运算速度[4].在传统DA算法中,当阶数增大时,查找表的规模将呈指数倍增加,需要使用多个查找表,受限制较大,并且当输入数据的位宽B增大时,累加运算也将增加,导致工作速度降低,难以满足高阶滤波及高速系统的要求.
不少学者对传统DA算法改进实现进行了研究,旨在设计更高速率的滤波器.文献[5]采用了OBC编码(即偏移二进制编码),其基本原理是在分布式算法中,将输入数据通过OBC编码由{0,1}映射到{1,-1},使得ROM表的上下两部分具有镜像对称性关系,利用这种对称性可以将ROM压缩一半.文献[6]采用多路选择分解思想,使用多个双向选择器,把寄存器输出的最高位不断反复地从LUT分离出来,由一个双向选择器和一个全加器来代替这部分LUT,从而进一步减小了查找表消耗,但是却增加了寄存器的使用,处理速度无法得到改善.文献[7]利用滤波器系数的对称性,能够降低接近一半资源的使用.上述算法查找表结构均是基于ROM实现,当阶数较高时,耗费ROM的数量十分可观,且由于采用连续寻址方式,ROM表中占用了许多不必要的存储单元,从而造成了较大的资源浪费和实现复杂性.
本文对分布式算法进行改进:考虑到内插倍数是通过/内插“0”实现,当滤波器阶数为N阶,内插倍数为P时,输入序列和滤波器系数乘积的所有可能取值数目最大为2ceil(N/P);当利用ROM表实现时,其地址由输入序列的阶数决定,其规模为2N,包含2N-2ceil(N/P)个无效地址;若使用逻辑单元LUT代替存储ROM,并通过合理的表分割设计查找表可以大大减少地址位数,减少计算的复杂性,使高阶滤波器设计时不受硬件ROM大小和数量的限制,从而节约了存储资源的消耗,提高了寻址速度.在此基础上,利用FIR滤波器的对称性,通过增加流水线处理,进一步提升了算法性能,使得改进DA算法能满足高阶滤波及高速系统的需求.
1 分布式算法 1.1 分布式算法原理分布式算法是通过将采样信号序列和滤波器系数所有的可能乘积,映射到一数据表,充分利用ROM资源,通过读取数据表的方式来实现乘法运算,可以极大提高运算速度[8].
一个N阶线性FIR滤波器的差分表达式如下:

|
(1) |
其中,h(m)为滤波器系数,当滤波器性能确定时,h(m)是一组已知的常系数.
对于有符号数的DA系统,输入数据x(n)采用二进制补码形式表示,(B+1)位的x(n)用二进制补码表示为
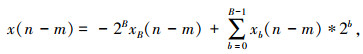
|
(2) |
其中,xb(n)表示x(n)第b位,大小为0或1,B表示输入数据的位宽.
将式(2)代入到式(1)中进行化简,可得到DA算法的表达式为
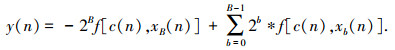
|
其中,
| 表 1 查找表内容 |
分布式算法的核心思想可概括为将输入数据进行二进制位分解,并进行位重组,将不同时刻的数据位取出构成新数据作为查找表的地址,而查找表中按地址索引存储着相应的乘积结果,以此方式完成乘法运算,后续通过移位累加等操作得到最终结果.
1.2 分布式算法实现结构分布式算法的实现结构包括三种:并行结构、串行结构和串并行结构相结合.不同实现结构占用的资源和运算速度不同.实际应用时,需要根据不同的设计指标,合理选择结构.
串行结构[9]在实现时,首先由移位寄存器将N个x(n)的每一位从低到高串行输入到查找表中,采用B个时钟周期串行求得B个f[c(n), xb(n)],每个f[c(n), xb(n)]由相应的二次幂加权后累加求和.串行工作方式运算速度较慢,每B个时钟周期只能得到一个输出,是一种使用资源换取效率的方法.
全并行分布式算法[10]实现时,将N个x(n)的各位并行输入,在一个时钟周期内同时求得B个映射f[c(n), xb(n)],各个映射根据所在的位数进行相应的二次幂加权,并将加权结果累加,在N次查询循环后就完成内积计算.
如果对运算速度要求适中,则可以设计成串并行结合的工作方式.可以将B位的采样数据按照一定的方式分割成L段,每一段使用一个ROM表,共使用L个ROM表,此时系统的时钟频率是采样频率的L/B倍.当B=L时,即为全并行结构,B=1时,即对应串行结构.
当滤波器阶数为N,位数为B时,分成L段,采样频率大小为f,则串行、并行、并串行结合的查找表结构的速度和资源对比情况如表 2所示.可以看出,这三种结构对ROM位宽的要求相同,但是串行分布式结构的速度最慢,消耗ROM的个数最少;并行结构则刚好相反;串并行结构达到了速度和资源的折中.
| 表 2 不同查找表结构的速度和资源对比 |
不管是串行、并行还是并串行结合的查找表结构,查找表的规模都会随着阶数N的增大而呈现指数增长.如果要设计N阶滤波器,查找表LUT规模为2N个字,这是很不经济的,必须减少所需查找表的规模.为了进一步缩小LUT规模[11],本文在分布式算法的基础上,通过采用FIR滤波器的对称性和表分割技术,降低了资源的使用率;通过使用并行分布式算法,提高了运算速度;结合改变查找表实现方式和增加流水线结构,使系统性能得到了进一步的优化.
假定一个NL阶滤波器,可以将NL个系数分成L组,每组对应一个查找表,即用L个独立的N阶串行DA的LUT输出之和替代一个NL阶的LUT输出,即

|
这样就可以将查找表的规模从2NL变为L*2N,分割后的LUT规模大大减小.同时,由于脉冲成形滤波器的设计主要通过FIR滤波器实现,其系数具有对称性.这样,可以求解的滤波器的系数就变为原来的二分之一,相同的系数可以共用一个查找表[11].
算法思想如图 1所示.

|
图 1 改进DA算法思想 |
为了能够提高系统的最大速度,将输入的基带信号分成高位和低位,并行进行处理.当阶数较大时,可以通过分割表降低表的规模.以升采样倍数16,阶数为97阶的升余弦滤波器为例,考虑到表的位数及计算方便性,总体可以分成3个表进行计算(97=2*16*3+1).此时每个表只需要存储16位的波形数据.
由于内插处理方法是在两个信号采样点间插入0,此时97个输入数据中实际上只有3个数据不为0,其他的点都是0.这些点对输出结果没有影响,此时将输入数据和系数进行相乘,每个查找表值只需要计算少数几个地址的取值.以查找表 1为例,有效地址如图 2所示.

|
图 2 查找的有效地址 |
此时可以进一步减少计算量.由于查找表的容量已经大大降低,如果选用ROM作为存储器,地址位数仍然较大,存储深度为216,实际上有效地址仅为13位,这是一种极大的浪费.因此,本设计主要使用CASE声明来定义分布式算法表,合成器可以使用逻辑单元来实现LUT,大大降低了硬件的消耗.同时,使用流水线实现加法功能,虽然增加了资源的利用率,但系统的整体速度却获得明显提升.
3 改进算法的硬件仿真及验证 3.1 参数设置1) 选用Altera公司的EP4SGX70HF35I3 FPGA芯片构建的硬件平台进行测试.
2) FIR脉冲成形滤波器参数:内插倍数为16,阶数为97,滚降系数设为0.4,截止频率设置为码元速率的一半.采用改进的全并行分布式DA算法,并加上流水线寄存器来实现.
3) 输入序列为经过16倍内插之后的双极性不归零码.
在上述条件下,编写Verilog代码.其中,FIR滤波器系数均由MATLAB产生,设计步骤如图 3所示.

|
图 3 脉冲成形滤波器设计步骤 |
硬件实现上,使用自顶向下的设计方法,针对系统的各个模块,进行原理分析和算法仿真,采用DA改进算法设计上述参数的升余弦滤波器.将程序下载到硬件测试平台,使用STP观测输出波形,与MATALB仿真结果进行对比,验证系统的正确性. 图 4所示为MATLAB理论仿真结果,上面是基带信号源,下面是冲成型滤波的输出;图 5所示为实际硬件仿真时,STP的输出波形,从上往下依次为基带信号源、内插升采样、脉冲成型滤波之后的波形.

|
图 4 MATLAB仿真结果 |

|
图 5 STP输出波形 |
对比图 4和图 5可知,在400 MHz的高速工作时钟下,输出结果理想,没有毛刺,硬件测试电路输出波形与理论仿真结果一致,验证了本算法在高速时钟下的正确性.
3.3 与商用IP核的性能对比开发环境Quartus Ⅱ V11.1中FIR Compiler的IP核和本文所提的改进DA算法都能完成要求的功能,但是它们资源使用情况和硬件最大运行速度却有所不同,具体对比结果如表 3所示.从表 3可以看出,改进DA算法没有使用Memory ALUT,而IP核使用2个Memory ALUT,同时,改进DA算法总体使用的寄存器资源要比IP核更少,且最大运行速度达到402 MHz,高于IP核.
| 表 3 改进DA算法和IP核算法对比 |
使用改进的全并行分布式算法和流水线设计结构,实现了高阶、高速的脉冲成型滤波器设计.硬件测试平台的测试结果,验证了设计的正确性和可行性.与商用IP核心实现方法相比,改进后的DA算法不仅没有利用ROM资源,而且其他逻辑资源也节约了10%,降低了系统的复杂度,能满足高阶滤波及高速系统的需求,最大运行速度相比IP核提高了近30%.
| [1] |
王方. 基带成形数字滤波器的设计[J]. 无线电通信技术, 2000, 26(5): 5-7. |
| [2] |
KIM M S, KIM D I, CHUNG J G, et al. Look-up table-based pulse-shaping filter design[J]. Electronics Letters, 2000, 36(17): 1505-1506. DOI:10.1049/el:20001024 |
| [3] |
HUANG W, KRISHNAN V. Design analysis of a distributed arithmetic adaptive FIR filter on an FPGA[J]. System & Computers, 2003, 1(9): 926-930. |
| [4] |
杨洪军, 王振友. 基于分布式算法和查找表的FIR滤波器的优化设计[J]. 山东理工大学学报(自然科学版), 2009, 23(5): 104-106. |
| [5] |
YOO H, ANDERSIN D V. Hardware efficient distributed arithmetic architecture for high-order digital filters[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Philadephia: IEEE, 2005: 125-128.
|
| [6] |
GUO R, DEBRUNNER L S. A novel adaptive filter implementation scheme using distributed arithmetic[C]//Proceedings of the Forty Fifth Asilomar Conference on Signals, Systems and Computers. Pacific Grove: IEEE, 2011: 160-164.
|
| [7] |
王学梅, 吴敏. 基于FPGA的分布式算法FIR滤波器的设计实现[J]. 世界电子元器件, 2004(10): 65-67. DOI:10.3969/j.issn.1006-7604.2004.10.017 |
| [8] |
刘俊, 刘会杰, 尹增山. 基于多速率的根升余弦滤波器的FPGA实现[J]. 现代电子技术, 2009, 32(19): 94-98. DOI:10.3969/j.issn.1004-373X.2009.19.031 |
| [9] |
LONGA P, MIRI A. Area-efficient fir filter design on FPGAs using distributed arithmetic[C]//IEEE International Symposium on Signal Processing and Information Technology. Vancouver: IEEE, 2006.
|
| [10] |
NARASIMHA M, PETERSON A M. On using the symmetry of FIR filters for digital interpolation[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1978, 26(3): 267-268. DOI:10.1109/TASSP.1978.1163094 |
| [11] |
PRAMOD K M, ABBES A. FPGA realization of FIR filters by efficient and flexible systolization using distributed arithmetic[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3009-3017. DOI:10.1109/TSP.2007.914926 |
 2016, Vol. 48
2016, Vol. 48





