2. 中国工程物理研究院 电子工程研究所, 621999 四川 绵阳
2. Electronic Engineering Institute, China Academy of Engineering Physics, 621999 Mianyang, Sichuan, China
工作于3~30 MHz的高频雷达具有超视距、散射截面大、数据率低等特殊优势,不论在军事还是民用上都有广泛而有效的应用[1].然而电离层杂波、海杂波、电台干扰等诸多不利因素的存在,增加了高频地波雷达目标检测的困难[2].
检测前跟踪TBD (track-before-detect)是在低信噪比情况下对目标进行检测和跟踪的一种技术,本质上是一种时域和空域的非相参方法[3-4].动态规划算法[5]是最常用的TBD实现算法之一,近年来对动态规划算法的研究主要是针对检测背景的特点做出相关改进和优化.文献[6-7]采用两级门限检测和方向加权方法来增强工程中的应用性;文献[8-9]针对多目标问题提出基于广义似然比检验的TBD算法并对目标数目问题进行了讨论; 文献[10]增加了航迹检测与校正方法,提高了跟踪概率.
极化信息是电磁波除幅度、频率、相位以外的一个重要基本参量,在雷达抗干扰、反隐身、目标检测等领域具有重要的应用潜力[11].本文针对高频地波雷达的极化特性,将极化信息引入TBD检测算法,并结合预处理方法和方向加权手段进一步提高TBD方法在高频地波雷达中的检测和跟踪性能.
1 雷达检测中的TBD算法 1.1 最优化原理动态规划算法的基本思想是将一个问题进行分解处理,处理过程可以采用状态变量来描述[12].设wi(xi, ui)是在第i个阶段在状态xi下运用决策ui得到的阶段指标函数.动态规划算法就是搜索整个过程,找到最优化轨迹使得阶段指标函数的累计值最大.最优性原理是动态规划算法的基本原理,最优性原理满足如下条件[13]:
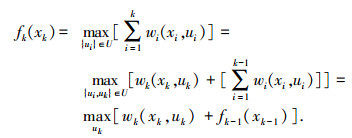
|
(1) |
式中:k为阶段数;U为决策变量ui限制的范围,称为允许决策集合.为满足递推关系,初始条件可以假设为
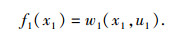
|
当动态规划算法用于检测前跟踪算法时,需要对动态规划的基本式变形,根据式(1)有
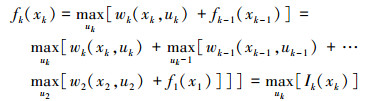
|
其中Ik(xk)表示阶段的值函数.值函数的选择直接影响算法对于目标检测的性能,因此对动态规划算法至关重要.在具体检测中,本文运用各阶段检测单元的幅度测量值zr, d(k)替代前面的wi(xi, ui)作为阶段指标函数[10],r,d分别表示距离单元和速度单元的序号.并得到以下的递推式:

|
(2) |
当基于最优性原理的动态规划算法应用于高频雷达在速度距离谱中检测时,初始条件要求对第一帧中的每个单元进行搜索,因此,初始条件为
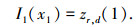
|
(3) |
在高频地波雷达目标检测中,按照式(2)和式(3)给出的递推关系,在K帧速度距离谱中进行搜索并对值函数累加.当完成所有搜索后,利用以下的判决方法判定目标是否存在,如果目标存在则对其轨迹进行估计:

|
式中: VT是判决门限; 
在高频地波雷达的速度距离谱中,目标的状态可以表示为xk=Zk(rk, dk),其中Zk表示第k个速度距离谱,r,d分别表示距离单元和速度单元的序号.在高频地波雷达背景下舰船目标认为是点目标,普通的军舰速度大概在20~30节之间.假设船速为最大速度30节,高频地波雷达载频8 MHz,积累时间为100 s,距离分辨力为1.5 km,则可知相邻两帧数据之间舰船的最大距离位移为2.3 km,即距离位移不超过2个距离单元.常规的高频雷达目标模型都是假设目标是匀速运动,然而在积累时间里,目标很有可能由于洋流、自身机动等原因,径向速度发生改变.假设目标在雷达探测期间在一个积累周期内,多普勒方向也最多移动一个多普勒单元[12],则高频地波雷达速度距离谱中不同积累周期之间状态转移过程存在一定联系.
假设第k帧数据目标状态为

|
则第k+1帧数据目标状态可能为
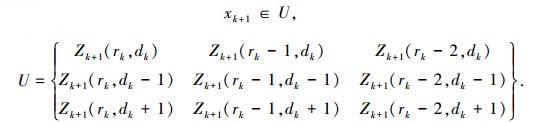
|
这里U是第k+1帧时目标的状态可能的范围集合,也就是第k+1帧目标状态可能是U中9个状态中的1个,这9个状态也被称为状态转移区域.
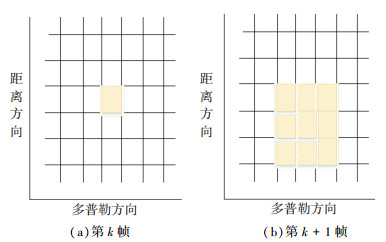
状态转移过程如图 1所示.
|
图 1 状态转移过程 |
设K时刻每个距离多普勒单元的目标功率强度为z(r, d)(k),则第k帧总的测量集合为
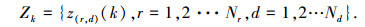
|
每个速度距离单元中又分为有无目标两种情况, 即
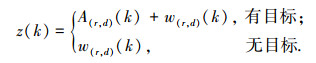
|
式中: A(r, d)表示目标的幅值; w(r, d)表示背景噪声,并假设噪声服从某种分布且是独立的.
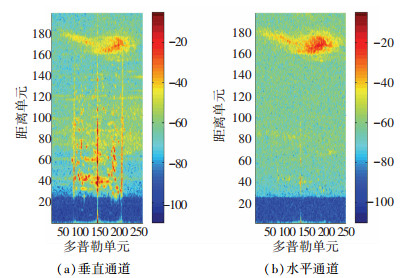
2 高频地波雷达极化特性 2.1 极化特性分析高频地波雷达的检测背景包含了电离层杂波、海杂波以及其他干扰和噪声.经典的恒虚警方法往往无法获得满意的检测性能,而使用TBD方法在复杂杂波环境下针对微弱目标的检测跟踪性能会大幅下降.因此,利用高频地波雷达电离层杂波和目标在极化特性上的差异,并结合高频雷达回波特性对算法进行改进是提高检测性能的重要方式. 图 2给出高频地波雷达实测数据垂直通道和水平通道的速度距离谱.
|
图 2 速度距离谱 |
由图 2可以看出, 高频地波雷达回波数据中出现大量杂波,其中电离层杂波几乎占据垂直通道和水平通道的整个距离单元[14].垂直通道有3条明显的竖线, 中间的能量很强部分是地物杂波,59和200附近的多普勒单元处主要是受Bragg峰影响.水平通道中目标和海杂波很少,但电离层杂波强烈,根据文献[15]可知这是因为电离层杂波的极化特性为椭圆极化,有部分分量进入水平通道,而目标和海杂波为线极化,主要进入垂直通道,被水平通道接收的很少.
通过垂直通道和水平通道可以计算对应的极化角谱,如图 3所示.

|
图 3 极化角 |
从图 3给出的极化角谱中可以直观地看到, 高频地波雷达的目标和电离层背景杂波之间有明显差异.目标极化角往往分布在70°以上,而电离层杂波极化角在0~90°之间都有分布,且随距离单元变化有一定规律性.
综合图 2中垂直通道的功率信息和图 3中极化角信息,对不同区域电离层杂波和目标的极化角及功率进行统计可以得到如图 4所示的极化角功率分布谱.

|
图 4 极化角功率分布谱 |
图 4中强电离层杂波是指分布在151~194距离单元的电离层杂波,该区域杂波能量较强但杂波极化角远小于目标极化角.弱电离层杂波是指分布在1 150距离单元上的电离层杂波,该区域杂波功率总体小于目标,但部分杂波极化角较大.
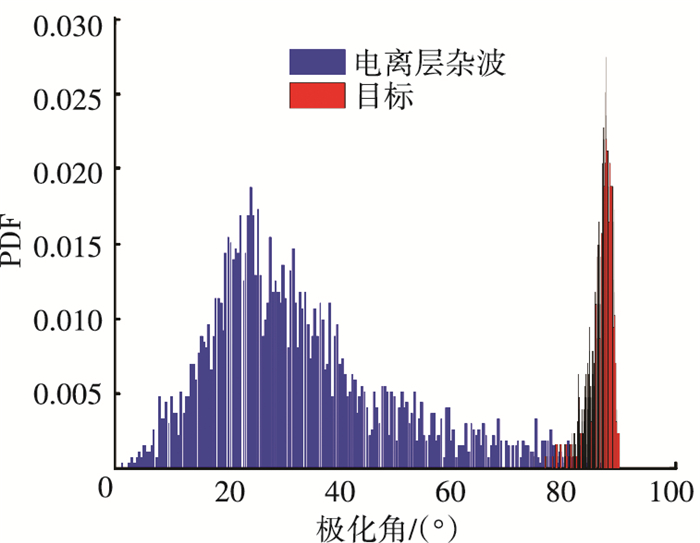
图 5给出部分距离单元上目标和杂波极化角统计结果.由图 5可以看出,目标的极化角和电离层杂波极化角存在差异,这为高频地波雷达的极化信息检测提供了基础.
|
图 5 目标和杂波极化角统计 |
低速运动的舰船目标,其多普勒谱往往会落入强烈的一阶和二阶Bragg散射当中,因此海杂波将构成对目标信号最大的干扰.由于海杂波的强度要高于或接近目标的散射强度,当目标的径向速度引起的多普勒频移接近或处于一阶谱的位置时,目标回波信号就会完全被一阶谱所掩盖,导致无法对目标有效检测.目前对于落在一阶谱区内的舰船目标检测,还没有特别行之有效的方法,只能根据一阶谱的位置,避开它对检测的干扰.
在TBD检测算法中,海杂波会使目标航迹发生偏移,从而失去对目标的追踪.一阶谱尽管能量很大,但是谱宽较窄,因此高频地波雷达在实际目标检测时,先通过人工方法剔除海杂波,再进行相关检测[13].
3 基于极化信息的高频雷达TBD检测方法 3.1 TBD方法在高频地波雷达中的改进措施 3.1.1 极化信息的应用通过前面统计分析可知,高频地波雷达目标和杂波在极化特性上有着明显差异[16],在进行TBD检测时有效利用高频地波雷达的极化特性将大大改善检测性能.假设利用动态规划算法TBD检测时每次扫描时的状态为Xk,阶段指标函数为z(Xk),利用目标和杂波的极化信息对价值函数进行修正,即令
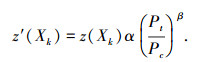
|
式中:Pt是对应检测位置的极化角,Pc是对周围杂波极化角的估计值,α是一个加权因子,β是指数因子.经过大量数据验证,当α =1,β =1时相对合理.由检测因子表达式可以直观看出,若待检测单元为目标,则其极化角Pt要大于杂波极化角估计值Pc,此时阶段指标函数z′(Xk)大于常规TBD算法的阶段指标函数z(Xk),有助于提高检测概率.若待检测单元为杂波,则其极化角小于或近似等于杂波极化角估计值,此时阶段指标函数近似等于或小于常规TBD检测算法的阶段指标函数,可以在一定程度上减小虚警率.
3.1.2 数据预处理庞大的雷达回波数据给TBD算法进行实时性检测提出了更高的要求,同时引入极化信息在改善检测性能的同时也会增加计算量.为了降低TBD的运算量,提高处理速度,在第一级采用低门限的单元平均选大恒虚警率处理方法.对第m个多普勒单元上的第n个距离单元,分别对前后参考窗内L个噪声距离单元进行平均处理,得到两个独立的噪声功率的估计值,记为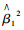
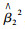
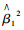
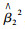
由前面高频地波雷达的状态转移分析过程可知,对于高频地波雷达的速度距离谱中可检测的舰船目标,在正常情况下,或朝雷达方向前进,或远离雷达方向运动,且在相邻积累时间内目标速度不会发生很大变化.如图 6所示,假设k-2帧中目标位置为xk-2(rk-2, dk-2),k-1帧中目标位置为xk-1(rk-1, dk-1),第k帧目标可能所处位置为xk(rk, dk),那么第k帧中目标在直线周围出现的可能性很大.

|
图 6 方向加权示意 |
因此一旦利用前面几帧确定目标运动方向,则可以利用运动规律对下一帧内不同搜索区域的方向加权.即给可能性较大的区域中的点给予较大的方向权重,而对远离前进方向区域中的点给予很小或为零的权重,以降低某些方向上噪声或干扰的影响,因此目标函数递推式可以改写为
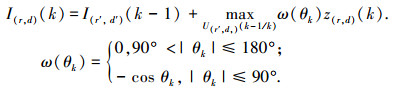
|
其中

|
首先对每一帧回波数据中海杂波进行剔除,k=1时第一帧数据的所有数据单元进行恒虚警预检测处理,将超过恒虚警门限的数据单元的相关信息记录为I(r, d)(1),即
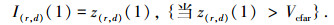
|
其中1≤r≤M,1≤d≤N,Vcfar是恒虚警检测门限. k=2时有
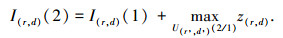
|
当k=3, …, K时,对前一帧中每一个积累量I(r, d)(k-1)所对应的RD单元(r,d),确定其在当前帧(即第k帧)中的参考空间搜索范围,并对该区域内的数据单元进行恒虚警处理.对于超过恒虚警门限的数据单元,先在对应的极化角谱里计算其极化角,再估计周围参考单元的极化角,利用价值函数z′(r, d)(k)=z(r, d)(k)
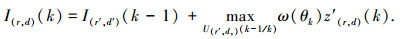
|
式中U(r′, d′)(k-1/k)是以第k-1帧中的I(r′, d′)(k-1)对应的数据单元为中心,在第K帧数据中的搜索范围,即参考空间.如果上述参考空间中没有数据单元能够超过恒虚警门限,则抛弃该I(r, d)(k-1).
3.2.3 轨迹判决k=K将最后一帧所有扫描完成后剩余的累积量记为IK,如果IK中某个元素I(r, d)(K)超过门限,则判定该(r, d)数据单元中存在目标,再根据I(r, d)(K)中记录的数据单元坐标信息进行归集回溯,即可同时得到目标的航迹.
3.3 性能分析此处检测概率定义为至少存在一个与真实目标的位置、速度在允许误差范围之内的xK使得最后状态的值函数超过检测门限的概率,即
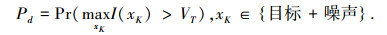
|
虚警概率定义为最大噪声状态的值函数超过检测门限的概率,即

|
式中VT表示检测门限,可以通过计算得到.由文献[13]可知
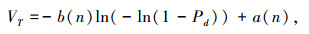
|
其中
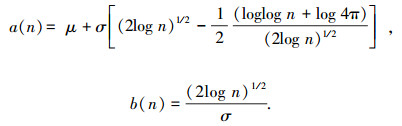
|
式中:n=N2×M2,N为距离单元数,M为速度单元数;μ和σ分别为积累K帧时沿着目标积累得到的值函数的均值和标准差.
4 实验仿真 4.1 高斯杂波背景仿真为简化仿真过程,设杂波背景为高斯白噪声,为了同时能够应用到极化信息,假设仿真目标极化角为88°,背景杂波极化角即为图 3所示的极化角谱.非起伏的单目标匀速运动,每帧分别向x,y方向运动一个单元,起始位置为(30,30),其中扫描15帧,图 7给出当信噪比为12 dB时的航迹图.

|
图 7 高斯背景下航迹 |
由图 7可以看出,传统TBD检测算法有3个点的跟踪误差,而基于极化信息的TBD改进算法能准确跟踪绝大多数仿真目标,说明改进后算法的检测和跟踪性能较传统算法有所提高.
图 8给出不同TBD检测策略的检测概率,检测门限VT=26.6.图中加权TBD是指在传统TBD基础上采用方向加权的方法,极化TBD指传统TBD基础上引入极化信息(具体来说是极化角信息)后的改进算法,TBD新算法是指综合应用方向加权、极化信息和预处理方法的检测算法.

|
图 8 高斯背景下检测性能 |
从图 8中可知,在高斯背景下,方向加权使TBD算法性能提高约1 dB,极化信息的加入使改进后的算法信噪比改善约2 dB,而既有方向加权又利用极化信息的TBD新算法相对传统算法性能明显改善.说明基于极化信息的TBD新算法在高斯背景中有着更优异的检测性能.
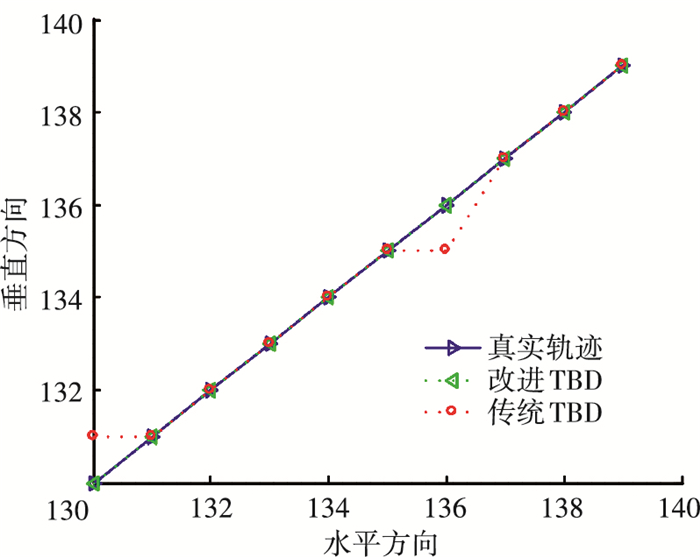
4.2 TBD检测新算法在高频地波雷达实测数据中的应用事实上,高频地波雷达实测数据相比高斯背景检测环境更为复杂,不仅有大量杂波存在,检测时真实目标之间也有可能相互干扰.为了进一步验证基于极化信息的TBD检测算法在高频地波雷达实测数据中的检测性能,在距离单元为194,多普勒单元为256的速度距离谱中加入仿真目标进行检测.设仿真目标起始位置为(130,130),选择该区域的主要原因是该区域中杂波主要是电离层杂波,可以避免海杂波影响,同时该区域很少存在真实目标,因此可以减小真实舰船目标对仿真目标的影响.为方便起见并不失一般性,假设仿真目标每帧以一单元的速度分别向距离向和多普勒向运动,扫描10帧. 图 9给出在信噪比为20dB时传统TBD算法和改进后TBD检测算法的航迹跟踪结果.
|
图 9 实测数据中仿真目标航迹 |
从图 9可以看出,传统TBD算法虽然能够恢复大部分目标的航迹,但对部分点航迹恢复结果与真实航迹存在偏差,而基于极化信息的TBD检测新方法可以准确地恢复航迹.
为了分析不同的改进措施对TBD算法性能提升程度,图 10给出高频地波雷达实测数据中加入仿真目标后分别使用传统TBD方法、方向加权TBD方法、极化加权TBD方法和综合利用方向及极化信息进行优化的TBD新方法的检测性能曲线,由于高频地波雷达回波数据幅值很小,因此经过计算得到的检测门限VT= 0.054.

|
图 10 不同算法实测数据中检测性能 |
从图 10不难看出,在高频雷达实测数据中传统TBD检测算法性能最差,利用方向加权的优化算法可以获得大约1dB的性能改善,采用极化信息的TBD改进方法性能进一步提高,而综合利用方向信息和极化信息的TBD新方法检测具有更优的效果.
为了验证TBD检测算法在高频地波雷达系统工程应用中的检测性能,在实测数据中进行真实舰船目标的检测.由于实测数据中的目标众多,为了便于分析,选择速度距离谱中的2个典型区域进行验证:区域1(125-175距离单元,120-200速度单元)主要验证强电离层杂波背景中的真实目标检测;区域2(25-60距离单元,50-170速度单元)验证弱电离层杂波中的真实目标检测. 图 11给出其中剔除海杂波和地物杂波后第一帧数据的速度距离谱.

|
图 11 剔除海杂波后检测背景 |
图 12给出使用传统TBD算法检测和航迹恢复的结果.在图 12中,(130,130)单元处的是图 9中的仿真目标航迹,其余为对实测数据中真实目标的检测航迹.由图 12可以看出,传统TBD算法可以从高频地波雷达中检测出相应的舰船目标,并且检测结果较恒虚警方法检测结果更加直观可靠,但是160距离单元附近的电离层杂波也被检测到并形成杂乱的航迹(已确认该区域中没有真实目标).这说明传统TBD方法虽然可行但是有一定局限性.

|
图 12 传统TBD方法检测 |
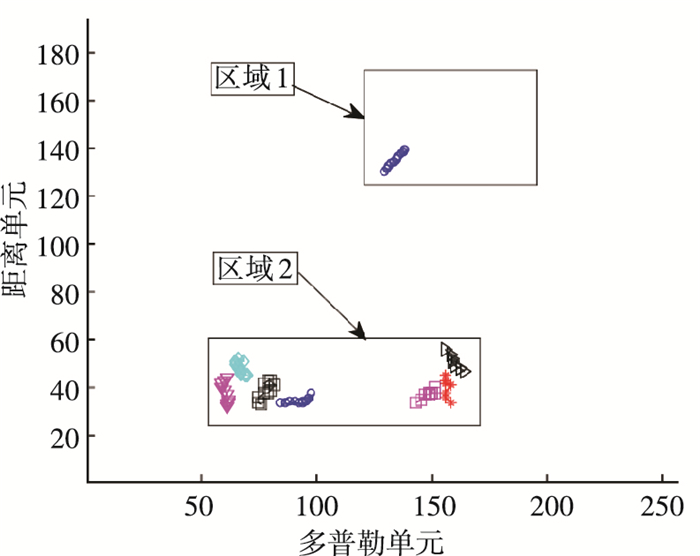
图 13给出使用基于极化信息的TBD新方法的航迹检测结果.从图 13可以看出,基于极化信息的TBD检测新方法在同样的背景中检测时,160距离单元附近的电离层杂波已经被压制,这是因为该区域电离层杂波极化角较小,通过极化加权使得该区域积累得到的值函数降低而低于最终检测门限.此外,对比图 12和图 13可以发现,使用基于极化信息的TBD检测算法在同条件下多检测出一条航迹,并且部分航迹更加明显,这说明改进算法相对于传统算法不仅发现概率有所提高,而且航迹跟踪效果也有所改善.
|
图 13 TBD新方法检测结果 |
1) 经典检测算法如恒虚警检测算法无法在高频地波雷达中获得良好的检测性能,检测前跟踪算法可以通过多帧累加获得一定的信噪比来检测目标,但是在复杂的海态和小目标环境下,常规动态规划算法检测跟踪性能欠佳.
2) 在TBD检测算法中引入极化信息,并结合方向加权方法和预处理手段对检测算法做出改进.仿真结果表明基于极化信息的TBD检测新算法在杂波背景下检测概率有所提高,得到的航迹更加准确.
| [1] |
SUN Minglei, XIE Junhao, JI Zhenyuan, et al. Remote sensing of ocean surface wind direction with shipborne high frequency surface wave radar[C]//Radar Conference (RadarCon 2015). Arlington VA: IEEE, 2015: 39-44.
|
| [2] |
DZVONKOVSKAYA A, ROHLING H. Fast-moving target observation using high-frequency surface wave radar[C]//Radar Conference (RadarCon 2014). Lille: IEEE, 2014: 1-4.
|
| [3] |
APRILE A, GROSSI E, LOPS M, et al. An application of track-before-detect to sea clutter rejection: experimental results based on real data[C]//European Microwave Conference. Rome: IEEE, 2014: 1808-1811.
|
| [4] |
YI W, MORELANDE M R, KONG L, et al. An efficient multi-frame track before detect algorithm for multi-target tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 421-434. DOI:10.1109/JSTSP.2013.2256415 |
| [5] |
GROSSI E, LOPS M, VENTURINO L. A novel dynamic programming algorithm for track-before-detect in radar systems[J]. IEEE Transactions on Signal Processing, 2013, 61(10): 2608-2619. DOI:10.1109/TSP.2013.2251338 |
| [6] |
BUZZI S, LOPS M, VENTURINO L. Track-before-detect procedures for early detection of moving target form airborne radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 937-954. DOI:10.1109/TAES.2005.1541440 |
| [7] |
ORLANDO D, VENTURINO L, LOPS M, et al. Track-before-detect strategies for STAP radars[J]. IEEE Transactions on Signal Processing, 2010, 58(2): 933-938. DOI:10.1109/TSP.2009.2032991 |
| [8] |
ORLANDO D, RICCI G. Track-before-detect algorithms for targets with kinematic constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1837-1849. DOI:10.1109/TAES.2011.5937268 |
| [9] |
COLLINS M J, DENBINA M, ATTEIA G. On the reconstruction of quad-pol SAR data from compact polarimetry data for ocean target detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 591-600. DOI:10.1109/TGRS.2012.2199760 |
| [10] |
强勇, 焦李成, 保挣. 动态规划算法进行弱目标检测的机理研究[J]. 电子与信息学报, 2003, 25(6): 721-727. |
| [11] |
罗小云, 李明, 左磊, 等. 基于动态规划的雷达微弱目标检测[J]. 系统工程与电子技术, 2011, 33(7): 1491-1496. |
| [12] |
夏共仪. 基于TBD方法的高频地波雷达弱目标检测与跟踪技术研究[D]. 哈尔滨, 哈尔滨工业大学, 2008: 41-42. http://cdmd.cnki.com.cn/Article/CDMD-10213-2009229226.htm
|
| [13] |
赵宇. 基于动态规划的检测前跟踪算法研究[D]. 西安: 西安电子科技大学, 2012: 42-44. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013112796.htm
|
| [14] |
MAO X, HONG H, DENG W, et al. Research on polarization cancellation of nonstationary ionosphere clutter in HF radar system[J]. International Journal of Antennas and Propagation, 2015, 2015: 1-12. |
| [15] |
刘爱军. 基于极化信息的高频地波雷达干扰抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2014: 106-108. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D264108
|
| [16] |
洪泓, 毛兴鹏, 果然, 等. 基于距离-多普勒域的电离层杂波极化抑制方法[J]. 系统工程与电子技术, 2014, 36(12): 2400-2405. |
 2016, Vol. 48
2016, Vol. 48


