随着编码技术的发展,各种熵编码方法应运而生,如香农编码、霍夫曼编码、算术编码、区间编码等.熵编码的编码性能主要依赖概率估计模型与信源的实际特性相符的程度.根据待编码数据的统计特性不同,熵编码的概率估计方法也有相应的不同.当待编码数据特性平稳时,经典的概率估计方法是最大似然法和贝叶斯参数估计法[1];当待编码数据特性非平稳时,主要的概率估计方法为基于“遗忘因子”的方法和加窗法.
贝叶斯参数估计法理论依据较强,先假定待估计参数具有某种先验分布,然后根据不断观测到的值去加强其中某种可能分布的可能性.由于对于平稳信源,参数的真实分布θ可看成不随时间改变的,因而随着观测数据的增加,贝叶斯估计
文献[3]提出基于“遗忘因子”的想法,当已编码字符总数达到一个事先设定的阈值时,将各种类字符的累积频率乘上一个大于0小于1的实数,称为“尺度调节(rescaling)”,所乘的实数叫做“遗忘因子(forgetting Factor)”.而加窗法是通过分析一段特定缓存中的内容去估计信源当前待编码符号的概率分布,这段缓存中存有W个之前已编码的字符(即缓存长度是W,也可称为窗长),每编码完一个新字符后,缓存中的内容会进行一次移位,新字符存入到缓存中,最早进入缓存的字符被删除.文献[4]从理论上分析了加窗法在非平稳环境下的编码性能,并讨论了窗长与编码冗余的关系.
近年来,弱估计算法为非平稳数据的概率估计供了新的思路,其中有代表性的是随机学习弱估计SLWE(stochastic learning weak estimator),它是一种基于学习自动机LA(learning automata)理论的参数估计方法. LA属于机器学习中的增强学习,文献[7]提出,最初用于模拟生物在出生时具备很少的先天知识,不断与随机环境交互下的学习过程. Oommen及其合作者提出了在非平稳环境下估计二项式和多项式分布的方法[5-7]. SLWE应用在概率估计中,可节省加窗法的窗口中数据缓存的存储空间,同时对于非平稳数据有了更强的适应性,并对多种类型的数据编码均可使用[8].
文献[9]曾尝试将SLWE概率估计方法应用FANO编码这种并不常用的熵编码中,并给出相应的实现方法.为拓展SLWE原理在熵编码中的应用,更有效的实现对非平稳数据的压缩编码,将其在编码性能更优良的区间编码上进行实现.区间编码是由Martin提出[10],与算术编码本质上类似,尽管在精度上稍微逊色,但比算术编码在频度统计中速度快很多[11].将SLWE概率估计方法应用到区间编码时,把原本的由概率更新改变各字符所占区间大小,从而通过总区间上下界的变化进行区间更新的方式,改进为将SLWE算法直接应用到对各字符所占区间大小的改变上的方法,不先进行概率更新的计算,而是直接用SLWE算法中的思想对各字符所占区间大小进行更新,再根据区间编码中总区间上下界计算方法来调整总区间大小,既结合了SLWE对非平稳数据概率估计的优势,又避免了概率的具体运算.从而提高编码过程对非平稳数据压缩编码的运算精度以及编码效率.
1 基于随机学习弱估计的概率估计方法 1.1 二项分布的SLWE概率估计过程二项分布又称伯努利分布,其特征由两个参数决定:试验的次数n和每次试验成功的概率p,如果将二值信源每次产生二值符号的过程看做一次伯努利试验,那么二项分布的参数估计问题就可看作通过编码二值序列对信源特性进行估计的问题.假设X是一个二项分布的随机变量,取值为“1”或“2”,并且X遵循概率分布Q=[q1, q2]T,即

|
其中q1+q2=1.
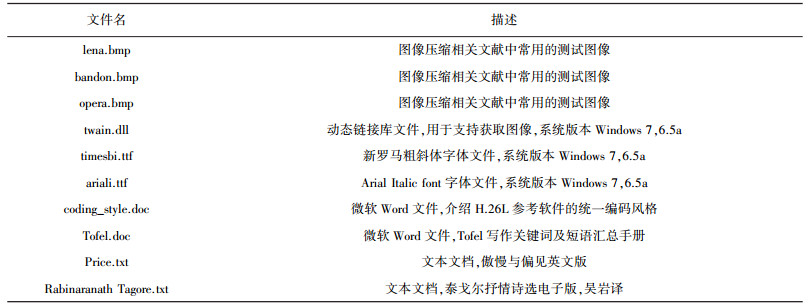
设X(n)是随机变量X在时刻n的具体值,根据SLWE理论,对于X(n)的概率估计是一个动态的过程,设对X(n)概率估计为P(n)=[p1(n), p2(n)]T,如果有参数λ称为学习因子(0<λ<1),则其概率更新方式如下:
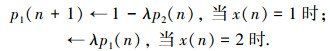
|
(1) |
与二项分布一样,多项分布的特征也由两个参数决定,即试验的次数n和决定试验结果的一个矢量,该矢量描述了一个事先给定的事件集合中某一特定事件发生的概率.同样的,可将多项分布的参数估计问题看成多值信源的特性估计问题.假设X是一个服从多项分布的随机变量,其真实概率分布为Q=[q1, …, qr]T,其中X = ′i′的概率为qi,
同样,令x(n)为变量X在n时刻的实际观测值,假设n时刻对Q的概率估计矢量为P(n)=[p1(n), …, pr(n)]T,其中pi(n)表示在n时刻对qi的估计,则根据SLWE理论,pi(n)更新方式如下

|
(2) |
式中i, j为多项分布X中的任意变量,且j≠i,参数λ称为学习因子,0<λ<1.
将运用多项分布情况下的SLWE概率估计方法,在信源信息为非平稳数据的情况下,对区间编码进行改进,以提高其编码性能.
2 区间编码方法一般的区间编码以各种符号的统计频率来估计概率,其编码端和解码端工作原理如下.
编码端:输入是信源符号集合S和待编码序列Z,输出是编码产生的码流Y.处理步骤如下:
步骤1 统计信源基本信息.以字节为单位读取待编码数据,统计待编码数据字节长度BBSIZE,字符种类数N.
步骤2 初始化概率估计模型.设定在n时刻总区间大小为R(n),信源符号集合S中各符号的频率为fi(n),其中i表示S中第i种字符(0≤i≤N-1),所有编码数据的总频率为FTF(n) (Total Frequency),
并且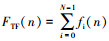
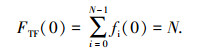
|
步骤3 根据序列Z中读入的符号,假设在n时刻待编码字符为第i种字符,设定ccumf(n)为前0到i-1种字符的累计频率,计算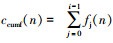
在n=0时刻,初始化累积频率为ccumf(0)=0.
步骤4 编码和区间规格化.首先定义在n时刻待编码字符i的概率为pi(n)=fi(n)/FTF(n),编码顺序在字符i之前的字符0到i-1的累计概率为ccump(n)=ccumf(n)/FTF(n),则当前总区间按照各个符号的概率进行更新,区间更新方法为

|
(3) |
式中:L(n)为总区间下界,R(n)为区间范围,L(n+1)为更新后的总区间下界,R(n+1)为更新后的区间范围,当更新后的区间范围小于指定阈值R0时,或者以字节为单位比较新区间的上下界并且上下界的高位字节相等时,移出高位的字节作为输出码流,同时对区间进行规格化处理.
步骤5 频率表更新,根据n时刻已编码字符i更新频率表.在字符i频率fi(n)的基础上加一个给定频率增量M,得n+1时刻的频率fi(n+1)=fi(n)+M,此时其他N-1种字符的频率不变,则总频率
同时对累积频率进行更新:

|
按照步骤3~5所述依次对所有8bit字符进行编码.为能够准确的进行解码操作,需要对最后一个符号的映射区间范围完全移出,同时保留该区间内某一个二进制数V,形成码流Y,并将其传递给解码器.
解码端:输入是编码产生的码流Y,信源符号集合S,输出是解码序列Z.处理步骤如下:
步骤1 读取信源基本信息以及待解码文件,得到原数据长度BBSIZE,符号种类数N,以及编码时保留的最后一个符号区间内的二进制数V.
步骤2 初始化概率模型,方法与编码端相同.
步骤3 计算累积频率估计值ccumfe(n),由公式

|
从而有

|
令ccumfe(0)=(V-L(0))/(R(0)/TTF(0)),得到累积概率的初始估计值,并且有估计不等式:

|
每编码一个字符,保持在当前n时刻的估计式ccumf(n)≤ccumfe(n)<(ccumf(n)+fi(n)),从而根据此式估计ccumfe(n)值.
步骤4 解码器解码与编码器编码保持一致,根据累计频率估计值,输出所在区间的字符,并更新当前区间范围,即

|
并判断是否需要区间规格化.
步骤5 根据步骤4中解码出的字符更新频率表,并根据当前区间范围以及新的频率表重新为各字符分配所属区间.
按照上述步骤3~5所述依次对所有8 bit字符进行编码,直到解码结束.
本文重点研究如何用SLWE算法实现编码端和解码端步骤5中概率更新的过程,并对实现过程中所遇到的相关问题给出解决和改进方法.
3 基于SLWE的区间编码设计方法首先通过对原区间编码过程的分析.
1) SLWE应用到区间编码中,核心是概率估计模型替换的过程,但同时会面临新的概率模型所估计出的概率如何映射到区间的问题.
在原区间编码中,各种字符在n时刻的估计概率是pi(n)=fi(n)/FTF(n),可知各种字符的概率更新是由频率的更新得到.并由式(3),每编码一个字符,按照相应各字符概率的变化来计算新的区间下界,从而将概率映射到区间,进行区间更新,最后根据区间的变化得到输出码流.
而SLWE应用到区间编码时,考虑区间编码的输出码流是由区间的不断更新变化得到的.因此,可将式(3)中R(n)×ccump(n)设定为n时刻待编码字符i之前的字符0~i-1的累积区间,即:CCUMR(n)=R(n)×ccump(n),同时将R(n)×pi(n)设定为n时刻待编码字符i所占区间的大小,即
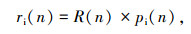
|
从而
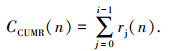
|
式中j为字符0到i-1.由此,在编码实现过程中,将各字符的概率pi(n)为成各字符所占区间ri(n),将各字符的总概率1等价于总区间范围R(n),即

|
同时,将SLWE应用到区间编码时,由于各种字符的估计概率是用区间代替的,在每编码一个字符时,总区间都会发生变化,相应的各种字符所占区间也需要进行同比例的缩放,从而才能保证当前各种字符的估计概率不变.因此,在每编码完一个字符时,记录下编码前后总区间的变化情况,编码前总区间为R(n),编码后总区间大小为R(n+1),每次编码之后记录下m=R(n+1)/R(n),则非待编码字符i所占区间更新为rj(n+1)=λ×[m×rj(n)],其中,j=0, …, N-1, j≠i.
2) 由于设定了各字符所占区间,而计算机实现时,区间是用整型数据表示,在对个字符所占区间进行更新时,更新后的各种字符所占区间大小可能出现小于1的情况,从而可能导致编码字符丢失的问题.
对此,对每种字符设定了最小区间r(n)min=R(n)×pmin≥1作为阈值,其中R(n)为当前总区间,Pmin为经验参数,从而保证每编码一个字符,总区间大小更新后,都会给出一个具体的最小区间,使得各字符所占区间的变化是有下限的,不能无限减小.当某一时刻计算出的某种字符所占的区间大小小于r(n)min时,以r(n)min作为该种字符的新区间.
综上所述,结合区间编码的整体框架,设计如图 1扭不的编码端其工作流程如下:

|
图 1 编码流程图 |
步骤1 统计信源基本信息.以字节为单位读取待编码数据,统计待编码数据长度BBSIZE,对不同种类符号编号的最大值为m0,符号编号的最小值为m1,符号种类数N=m0-m1+1,各符号种类分别用索引0, …, N-1表示;
步骤2 初始化.对32位系统,可初始化区间上界为H=0xffffffff,区间下界为L=0x00000000,则原始区间大小为R(0)=0xffffffff,初始化各个符号占据的初始区间长度为ri(0)=R(0)/N,i=0, …, N-1,初始化区间规格化时的临界阈值R0=0x00001000.
步骤3 根据读入字符计算累计区间长度.初始化累积区间长度CCUMR(0)=0,假设当前待编码字符索引为i,计算
步骤4 编码和区间规格化.记录当前区间长度R(n),然后根据当前待编码字符对区间进行更新,更新方式为:

|
当新区间长度R(n+1) ≤ R0或以字节为单位比较新区间的上界和下界,上下界的高位字节相等时,移出高位的字节作为输出码流,同时对区间进行规格化处理,具体做法为将R(n+1)和L(n+1)分别左移8位,即R(n+1)←R(n+1)≪8,L(n+1)←L(n+1)≪8.最后计算编码后区间和编码前区间的比值m=R(n+1)/R(n);
步骤5 更新概率估计表.根据SLWE算法,对各字符所在区间大小进行更新,具体过程与编码端相同.
Step 1 根据信源基本信息,给定参数pmin,并根据更新后的区间R(n+1)计算各字符所占区间的下限,即最小区间r(n+1)min=R(n+1)×pmin,初始化学习因子λ,设n+1刻除字符i外的其他字符所占区间为SSUMR(0)=0.
Step 2 依次计算序号为j=0, …, N-1, j≠i的字符所占区间大小.

|
其中j=0, …, N-1, j≠i.
Step 3 计算
Step 4 计算ri(n+1)=R(n+1)-SSUMR(n+1).
步骤6 编码收尾阶段.按照步骤3~5,对所有待编码数据进行编码.编码结束时,移出映射区间内所有的位.分别将码流和待编码数据的相关信息以文件形式保存.
同时设计了如图 2所示的解码端框架,工作流程如下:

|
图 2 解码流程图 |
步骤1 读取信源基本信息文件,得到原数据长度BBSIZE,对不同种类符号最大值m0,符号编码最小值m1,计算符号种类数N=m0-m1+1.
步骤2 与编码过程中的初始化过程一样初始化区间上界H=0xffffffff、区间下界L=0x00000000,初始化各个符号占据的初始区间长度ri(0)=R(0)/N,i=0, …, N-1,初始化区间规格化时的临界阈值R0=0x00001000.并以字节为单位读取码流文件,设定初始标识符T=0x00000000,通过计算机运算,将每4个字节码流信息存储于T.
步骤3 根据T和当前区间下界L以及各符号的区间长度进行解码,解码过程中得到当前符号的索引i.具体做法为寻找满足下述关系的i:

|
步骤4 首先记录当前区间长度R(n),然后根据i对区间进行更新,更新方式与编码过程中的更新方式一致,即

|
更新后的区间长度为第i种字符所在的区间长度ri(n+1),即R(n+1)←ri(n+1).当新区间长度R(n+1)小于指定阈值R0或以字节为单位比较新区间的上界和下界,上下界的高位字节相等时,对区间进行规格化处理,即:将R(n+1)和L(n+1)分别左移8位,R(n+1)←R(n+1)≪8,L(n+1)←L(n+1)≪8,同时以字节为单位读取码流文件并与T进行或运算,之后将T左移8位.计算编码后区间和编码前区间的比值m=R(n+1)/R(n).
步骤5 根据SLWE算法对各字符所在区间大小进行更新,具体过程如下:
Step 1 根据信源基本信息,给定参数Pmin,并根据更新后的区间R(n+1)计算各字符所在区间的下限R(n+1)min=R(n+1)·Pmin,初始化学习因子λ,定义变量SSUMR(0)=0.
Step 2 依次计算序号为,j=0, …, N-1, j≠i的字符所占区间大小

|
Step 3 计算
Step 4 计算ri(n+1)=R(n+1)-SSUMR(n+1).
输出此次解码后得到的字符,形成解码有序.
步骤6 当解出的数据总长度小于原数据长度BBSIZE时,重复进行步骤3、4、5.
4 实验结果及讨论实验中,对仿真数据在不同概率估计方法下的熵值进行分析和比较,验证基于SLWE的概率估计方法对信源熵值估计的有效性.并在试验中考察学习因子λ在何种范围下,概率估计的效果较好.对真实数据的编码实验中,应用已有的基于不同概率估计方法的区间编码原理,分别对不同的数据类型进行编码实验,并对相应的压缩率进行比较和有针对性的分析,从而验证基于SLWE的区间编码方法,在编码非平稳数据时的优越性.
4.1 面向仿真数据的概率估计实验本部分实验主要根据各概率估计算法对仿真数据的估计熵与其实际熵的偏离程度评价各算法的适用情况. 表 1是对不同特性仿真数据的真实熵值,静态模型以及add-half准则的估计熵,和用SLWE方法的估计熵之间的比较情况.其中,对于静态模型,在编码过程中概率模型不随时刻的改变而改变.静态概率模型的建立往往需要信源的先验知识,若没有相关的先验知识,可通过遍历整个待编码字符串,统计其分布特征来建立概率模型.
| 表 1 不同特性二值仿真数据的真实熵与各概率估计方法下的估计熵 |
“add-half”法则是由Krichevskii提出的对贝叶斯参数估计法的一种实现方法[12],从通用编码(Universal coding)角度来说,在贝叶斯参数估计法中,“add-half”法则是最优的.
仿真数据为二值伪随机序列,L表示某种给定概率特性的信源持续作用的时间,N为不同种类信源的个数,L越大说明某种信源持续作用的时间越长,表示其统计特性越平稳,N越大说明该仿真数据特性变化的越频繁,表示其统计特性越不平稳.另外,为了更贴近实际数据的特性变化,上述过程中的L可设置为可变的,这种情况下用Lmax为产生的数据中可能的最大平稳段数据长度.
实验中首先产生指定特性的仿真数据,然后分别计算仿真数据的真实熵以及用各种概率估计算法得到的概率模型下的估计熵(λ取0.9、0.95、0.99),为了消除仿真数据的偶然性因素影响,每组实验进行100次,取均值.
实验结果见表 1,当数据特性非平稳时(N=3, N=5的情况下),SLWE算法的估计熵更接近真实熵,并且学习因子λ不同,逼近程度也不一样.
图 3给出信源特性不同时,SLWE方法中不同学习因子λ下概率估计算法的概率估计曲线与反映信源真实特性的概率曲线之间的关系.从图中可以看出,λ的大小主要影响信源特性发生突变时概率估计曲线相对于信源真实特性变化曲线的滞后情况,λ较小时,概率估计曲线滞后较小,而λ较大时(接近1),概率估计曲线滞后较大.但λ较小时,概率估计曲线的波动较大,说明此时概率模型易受已编码符号中短暂的异常分布影响,而λ较大时,这种影响就很弱,表现为曲线波动较小.

|
图 3 不同学习因子λ下SLWE概率跟踪曲线 |
另外,对于表 1中给出的几种情况,均为λ=0.95时,估计效果最佳. 图 4是对于Lmax=10 000, N=10和Lmax=10 000, N=5两种特性的二值仿真数据分别在上述两种方法在给定参数选择范围下均选取最优参数时估计熵与真实熵的相对偏差曲线比较情况.从图中可看出,对于指定特性的仿真数据,两种方法在均选取最优参数的情况下,相对偏差曲线非常接近,SLWE算法略小于加窗法.

|
图 4 仿真数据两种方法选取最优参数时相对偏差曲线 |
本部分利用第3节中设计的基于SLWE概率估计算法的区间编码对真实数据进行编码实验,并与基于静态模型的区间编码和基于遗忘因子法的区间编码进行比较.
为验证本文研究的概率估计算法应用于实际熵编码器对于编码效果的影响,本文选取几种常见格式的真实数据进行熵编码实验,相关介绍见表 2.
| 表 2 实验数据及相关描述 |
数据的选取参考文献[13]中的数据选取方法,主要包括bmp图像、计算机中的系统文件、微软word文档和文本文档,所选数据中前8种数据属于非平稳数据,后两种Price.txt和Rabinaranath Tagore.txt属于平稳数据.由于SLWE法与遗忘因子法的概率估计效果均与参数有关,为了公平起见,实验中采用如下参数选取方式:遗忘因子法中设置β=0.5, Nmax=214,通过改变M调节算法的自适应能力,M调节范围为1~20,在给定的参数选择范围中选取压缩率最高的M值,记录下实验结果;对于SLWE法,设置Pmin=0.001,通过改变λ调节算法的自适应能力,λ的选取范围为0.9到0.99,间隔为0.01,同样在给定参数范围内选择压缩率最高的λ值,同样记录下实验结果.表中ly表示码流长度,B表示bytes,ρ为压缩率,最后一栏Ave/tol列出所有实验数据的总大小和压缩后数据的总大小以及对各数据压缩率的均值.
从表 3中可看出SLWE算法与遗忘因子法一样,在对非平稳数据进行概率估计时能较好的适应数据特性的变化,显著的优于静态模型的概率估计效果,并且与遗忘因子法相比,在选定的数据范围内,SLWE算法也优于遗忘因子法.这说明SLWE算法非常适合非平稳环境下的概率估计问题.
| 表 3 不同概率估计模型下的区间编码编码结果 |
本文以提高熵编码的编码性能为目的,以压缩率为指标,对熵编码中概率估计模型进行改进.编码器参考的概率模型是否符合信源的实际特性会直接影响最后的编码性能,当待编码数据特性非平稳时,概率模型的建立问题将变得很复杂,原始概率模型往往会与信源的实际特性有所偏离,影响编码性能,若概率模型能及时的反映待编码数据这种特性变化,理论上可取得更好的编码效果.
因此,本文设计基于SLWE的区间编码方法为使概率模型所估计出的概率更好的映射到区间,在实现过程中,用区间累加替代原算法中的概率累加.并且,通过设置最小区间避免了区间大小小于1的问题.在对不同特性的非平稳数据的概率估计仿真实验和实际编码实验中,本文方法效果比加窗法和遗忘因子法等方法更好,这说明SLWE算法比较适合用于非平稳数据的概率估计,同时改进后的区间编码的编码效率更高.
对于本文SLWE算法中的学习因子λ,通过仿真实验得到最佳数值.未来重点研究在于学习因子λ的选择方法,实现学习因子λ可调的概率估计方法.
| [1] |
DUTTWEILER D L, CHAMZAS C. Probability estimation in arithmetic and adaptive-Huffman entropy coders[J]. IEEE Transactions on Image Processing, 1995, 4(3): 237-246. DOI:10.1109/83.366473 |
| [2] |
MERHAV N, FEDER M. A strong version of the redundancy-capacity theorem of universal coding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 714-722. DOI:10.1109/18.382017 |
| [3] |
GALLAGER R G. Variations on a theme by Huffman[J]. IEEE Transactions on Information Theory, 1978, 24(6): 668-674. DOI:10.1109/TIT.1978.1055959 |
| [4] |
SSNEHAG P, SHAO W, HUTTER M. Coding of non-stationary sources as a foundation for detecting change points and outliers in binary time-series[C]//Proceedings of the Tenth Australasian Data Mining Conference-Volume 134. Australian Computer Society, Inc., 2012: 79-84.
|
| [5] |
YAZIDI A, OOMMEN B J, GRAMMO O C. A novel stochastic discretized weak estimator operating in non-stationary environments[C]//IEEE International Conference on Computing, Networking and Communications, 2012: 364-370.
|
| [6] |
TSETLIN M L. On the behavior of finite automata in random media[J]. Avtomatika I Telemekhanika, 1961, 22(10): 1345-1354. |
| [7] |
OOMMEN B J, RUEDA L. Stochastic learning-based weak estimation of multinomial random variables and its applications to pattern recognition in non-stationary environments[J]. Pattern Recognition, 2006, 39(3): 328-341. DOI:10.1016/j.patcog.2005.09.007 |
| [8] |
SUDIP M, SUKHCHAIN S, MANAS K. MIRACLE:Mobility Prediction Inside a Coverage Hole Using Stochastic Learning Weak Estimator[J]. IEEE Transactions on Cybernetics, 2015, PP(99): 1-12. |
| [9] |
RUEDA L, OOMMEN B J. Stochastic automata-based estimators for adaptively compressing files with nonstationary distributions[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2006, 36(5): 1196-1200. DOI:10.1109/TSMCB.2006.872256 |
| [10] |
MARTIN G N N. Range encoding: an algorithm for removing redundancy from a digitized message[C]//Proc. Institution of Electronic and Radio Engineers International Conference on Video and Data Recording. [S. l.]: [s. n.], 1979: 1-11
|
| [11] |
EVGENY B, LIU Kai, LI Yunsong. An Efficient Adaptive Binary Range Coder and Its VLSI Architecture[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(8): 1435-1446. DOI:10.1109/TCSVT.2014.2372291 |
| [12] |
KRICHEVSKIV R E. Universal Compression and Retrieval[M]. Dordrecht, the Netherlands: Kluwer, 1994: 217.
|
| [13] |
ROS M, CUELLAR M P, DELGDO M, VILA A. Online recognition of human activities and adaptation to habit changes by means of learning automata and fuzzy temporal windows[J]. Information Sciences, 2013, 220(10): 86-101. |
 2016, Vol. 48
2016, Vol. 48