共形阵列是由共形载体上的共形辐射单元构成的阵列, 具有节省空间、满足空气动力学要求、充分利用孔径等优点, 因此在星载、机载、弹载及通信领域有着广泛的应用前景.
目前对共形阵列的研究方向包括共形辐射单元设计及辐射特性研究[1-2], 共形天线的分析和综合优化[3], 共形阵列建模[4], 参数估计性能分析[5], 共形阵列参数估计算法[6-12], 以及共形阵列波束形成算法[13]等.在共形阵列参数估计算法方面取得的研究成果有, 文献[4]利用欧拉旋转变换完成了阵元极化方向图在全局坐标系下的表示, 给出共形阵列信号模型; 文献[5]研究了共形阵列条件下, DOA(direction of arrival)参数估计的CRB(cramer-rao bound)以及MUSIC算法的理论精度; 文献[6]针对由偶极子构成的锥面共形阵列, 基于旋转不变子空间思想, 给出了相干源条件下的极化-DOA联合估计方法; 文献[7]通过将柱面共形阵列划分为多个子阵利用MUISC算法实现了对二维DOA参数的估计; 文献[8]利用四阶累积量和ESPRIT(estimation of signal parameters via rotational invariant techniques, 旋转不变子空间)算法实现了共形阵列条件下的盲极化DOA估计; 文献[9]利用单曲率共形载体结构, 通过合理布阵和坐标系设置, 提出一种适用于柱面和锥面共形阵列的极化-DOA联合估计算法; 文献[10]利用多阶次的分数阶傅里叶变换将多分量线性调频信号在变换域进行分离, 并结合传播算子算法实现极化和DOA参数的估计; 文献[11]利用虚拟阵列实现共形阵列幅相误差校正, 并利用虚拟阵列的特殊结构快速实现对信源的DOA估计; 文献[12]将任意基线算法扩展到三维阵列中, 结合虚拟基线方法, 利用子阵分割技术和矩阵求逆方法得到二维DOA估计; 文献[13]基于共形阵列天线, 通过主瓣波束保形约束, 求解最优响应矢量, 方法保持了期望的主瓣响应, 并对阵列构型具有稳健性.
综上可看出, 在共形阵列参数估计领域的研究内容主要包括:信号建模[4], 参数估计精度分析[5], 不同条件下的参数估计算法[6-12]及波束形成算法[13].在共形阵列性能分析方面, 已有的研究成果[5]主要讨论的是共形阵列对DOA参数的估计精度以及DOA参数估计的CRB.分辨力描述的是阵列对参数接近信号的分辨能力, 是超分辨算法和共形阵列的一个重要性能, 在已有文献中并未发现相应的研究内容.本文首先通过欧拉旋转变化对共形阵列进行建模; 在此基础上, 通过MUSIC零谱的定义, 推导了MUSIC算法在共形阵列中的理论分辨力门限; 最后, 通过仿真研究分析了分辨力门限理论值与仿真值之间的关系, 以及共形阵列与平面阵列在分辨力性能上的差异.
1 共形阵列信号模型 1.1 共形阵列结构共形阵列的常见形式包括:锥面共形阵列, 柱面共形阵列和球面共形阵列, 其具体形式见图 1.由图 1可看出, 与传统平面布阵形式不同, 共形阵列的立体布阵形式在充分利用载体纵向孔径的同时符合空气动力学要求, 结合相应的信号处理算法可以实现高精度参数估计以及优越的分辨力性能.
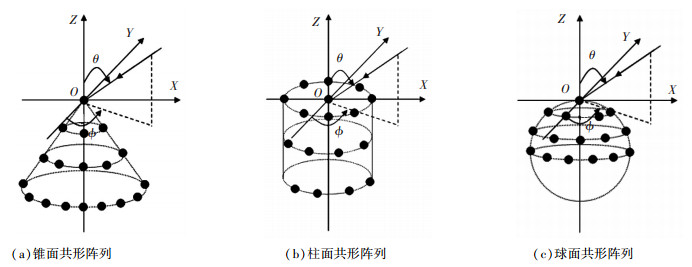
|
图 1 共形阵列示意 |
考虑有M个信源入射到由N个单极化共形天线单元构成的共形阵列上, 则其接收信号模型为
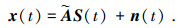
|
(1) |
式中: 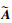
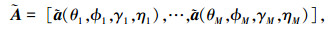
|
(2) |
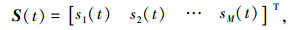
|
(3) |
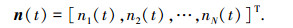
|
(4) |
共形阵列信号模型的关键是阵列导向矢量的建模, 阵列导向矢量的具体形式为

|
(5) |

|
(6) |

|
(7) |

|
(8) |

|
(9) |
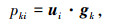
|
(10) |
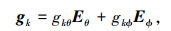
|
(11) |
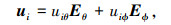
|
(12) |

|
(13) |
式(5)~(13)中: as(θi, ϕi)为导向矢量中的空域部分; ap(θi, ϕi, γi, ηi)为导向矢量中的极化部分; ⊙为矩阵的Hadamard乘积; ki为入射信号方向矢量; ln为阵元空间位置; pki为全局极坐标下, 第i个入射信号极化矢量在第k个阵元上的投影; gk为第k个阵元极化方向图的全局表示(方向图旋转变换的详细过程见文献[4]); ui为第i个入射信号的极化矢量.
与经典阵列不同, 共形阵列建模需要将共形天线单元的极化方向图在全局坐标系下表示, 然后将入射信号的极化矢量在全局坐标系下表示的阵元极化方向图上投影, 得到某个共形单元对入射信号的极化响应.这也是共形阵列信号建模的关键.
对于由N个双极化共形单元构成的共形阵列, 其阵列导向矢量仍可表示为式(5), 其元素具体构成为

|
(14) |

|
(15) |

|
(16) |

|
(17) |
式(14)~(17)中: as(θi, ϕi)为导向矢量中的空域部分, 为2N×1维列向量; ap(θi, ϕi, γi, ηi)为导向矢量中的极化部分, 为2N×1维列向量; pki为全局极坐标系中, 第i个入射信号极化矢量在第k个阵元水平极化单元上的投影; 


定义单极化阵元共形阵列的协方差矩阵为
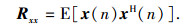
|
(18) |
对Rxx进行特征值分解, 有
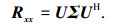
|
(19) |
式中: Σ=diag{σ12, σ22, …, σN2}为特征值对角阵, U为特征向量阵, 具体形式为

|
(20) |
共形阵列的极化-DOA联合谱为
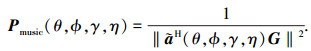
|
(21) |
双极化阵元共形阵列的MUSIC算法与单极化情况类似.由式(21)可看出, 极化-DOA参数的多参量估计是以(θ, ϕ, γ, η)四维联合谱的形式给出的, 正是通过对联合谱零谱的定义推导出共形阵列条件下的理论分辨力门限.
3 共形阵列MUSIC算法分辨力分析 3.1 联合谱分辨力定义分辨力性能反映的是算法对两个参数相近的信号源能否成功分辨的能力, 是极化-DOA联合谱估计算法的一项重要性能指标.文献[14]中的方法, 以零谱的形式给出联合谱分辨力的定义.
假设有两个等功率, 不相关且参数接近的信号源入射到共形阵列, 入射参数分别为(θ1, ϕ1, γ1, η1)和(θ2, ϕ2, γ2, η2).
定义两入射信号参数的中值点
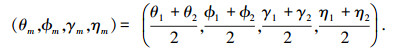
|
(22) |
定义联合谱的零谱

|
(23) |
对于联合谱的零谱若有
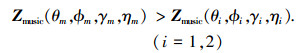
|
(24) |
成立, 则称联合谱是可分辨的, 对应的分辨力为

|
(25) |
由式(24)可看出, 联合谱可以分辨的定义为两个信号源参数中心位置处的谱值要低于两个信号源处的谱值.式(22)~(25)给出的是理想情况下的分辨力描述.
3.2 联合谱分辨力分析在实际应用中, 需要根据观测到有限的快拍数据估计阵列的自相关矩阵, 得到对噪声子空间的估计.此时定义联合谱零谱的估计值为
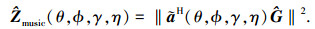
|
(26) |
定义零谱的期望为

|
(27) |
在实际应用中重新定义分辨力为:对联合谱的零谱来说, 若有

|
(28) |
则称联合谱是可分辨的.
定义理想情况下噪声子空间的投影矩阵为

|
(29) |
定义噪声子空间投影矩阵的估计值为

|
(30) |
定义噪声投影矩阵的误差为
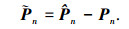
|
(31) |
噪声投影矩阵误差的期望为
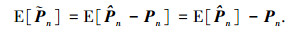
|
(32) |
由文献[15]可知

|
(33) |
式中: K为快拍数; N为阵元个数, 对单极化阵元共形阵列N为阵元数, 对双极化阵元共形阵列N为2倍阵元数; M为信号源个数, 在进行分辨力讨论时取M=2.式中其它符号定义为

|
(34) |
式中: λ1, λ2与u1, u2为对理想阵列协方差矩阵进行特征值分解得到特征值及与其对应的特征向量, 理想协方差矩阵的定义为
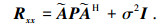
|
(35) |
式中: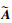
将式(34)代入式(33)并整理可得

|
(36) |
其中

|
(37) |
考察式(27)描述零谱期望值, 并由式(32)可得

|
(38) |
将式(36)代入式(38), 并整理可得

|
(39) |
其中
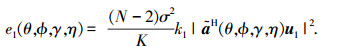
|
(40) |
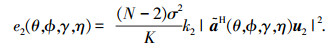
|
(41) |
式(39)可知, 在快拍数有限的情况下估计得到的联合谱零谱的期望由3项构成:联合谱零谱, 扰动项e1(θ, ϕ, γ, η)和e2(θ, ϕ, γ, η).
考虑到Zmusic(θ1, ϕ1, γ1, η1)=0, 在参数(θ1, ϕ1, γ1, η1)处联合谱零谱的期望为
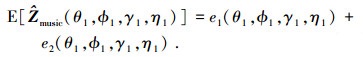
|
(42) |
同理, 在参数(θ2, ϕ2, γ2, η2)处联合谱零谱的期望为

|
(43) |
在(θm, ϕm, γm, ηm)处, 联合谱零谱的期望为
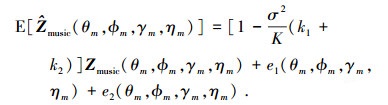
|
(44) |
由于
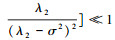
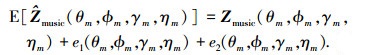
|
(45) |
根据式(28), 信号可分辨的条件可写为

|
(46) |
整理为
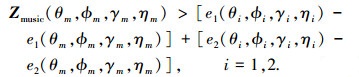
|
(47) |
由文献[15]可知, 当两个信号源参数接近时, e1(θi, ϕi, γi, ηi)-e1(θm, ϕm, γm, ηm)的影响可以忽略, 因此式(47)可进一步简化为
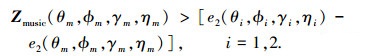
|
(48) |
式中ZMusic(θm, ϕm, γm, ηm)为理想情况下, 联合谱的零谱在(θm, ϕm, γm, ηm)处的值.
由以上讨论可知, 在阵列形式一定的情况下, 系统的分辨力性能主要取决于信噪比和快拍数.对入射参数接近的两个信号源, 若其联合谱的零谱在(θm, ϕm, γm, ηm)处满足式(48), 则认为这两个信号源是可分辨的.在信噪比一定的情况下, 可以由式(48)计算出成功分辨两个信号所需的快拍数, 同样在快拍数一定的情况下, 也可由式(48)计算得到成功分辨两个信号所需的信噪比.
4 仿真实验仿真实验1:考察基于共形阵列的极化-DOA联合谱估计.
仿真中取图 2所示的柱面共形阵列, 具体参数为:圆环阵个数3, 每个圆环上由8个均匀分布的阵元构成.每层圆环的半径为3λ, 圆环阵之间的高度为2λ.天线单元采用微带贴片单元, 方向图为[4]

|
图 2 单极化柱面共形阵列示意 |
当0≤θ≤π/2时:

|
(49) |

|
(50) |
当θ>π/2时:
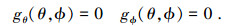
|
(51) |
式中: J0为零阶第一类贝塞尔函数, J2为二阶第一类贝塞尔函数.
仿真条件:入射参数(θ1, ϕ1, γ1, η1)=(15°, 50°, 45°, 90°), 信噪比10 dB, 快拍数500.由式(21)可得柱面共形阵列的极化-DOA联合谱估计仿真结果见图 3.

|
图 3 单极化柱面共形阵列联合谱 |
为便于显示, 将仿真结果分别投影到角度切片和极化切片上显示.角度切片是指固定搜索的极化参数与入射信号极化参数相同, 在角度域(θ, ϕ)进行二维搜索; 极化切片是指固定搜索的角度参数与入射信号参数相同, 在极化域(γ, η)进行二维搜索.
对单极化柱面共形阵列, 采用MUSIC算法得到对入射信号的联合谱估计结果见图 3.由图 3(a)可看出, 联合谱算法在角度切片上得到了对入射信号DOA参数的估计结果为θ= 15°, ϕ= 50°, 对应的谱峰高度为25.8 dB(图 3(a)所示的角度切片估计结果中X, Y, Z分别对应θ, ϕ估计值和谱峰高度).
由图 3(b)可看出, 联合谱算法在极化切片上得到对信号极化参数估计值为γ= 45°, η= 90°, 对应的谱峰高度为25.8 dB(图 3(b)所示的极化切片估计结果中X, Y, Z, 分别对应γ, η估计值和谱峰高度).
仿真实验2:考察由单极化阵元构成的柱面共形阵列的分辨力.
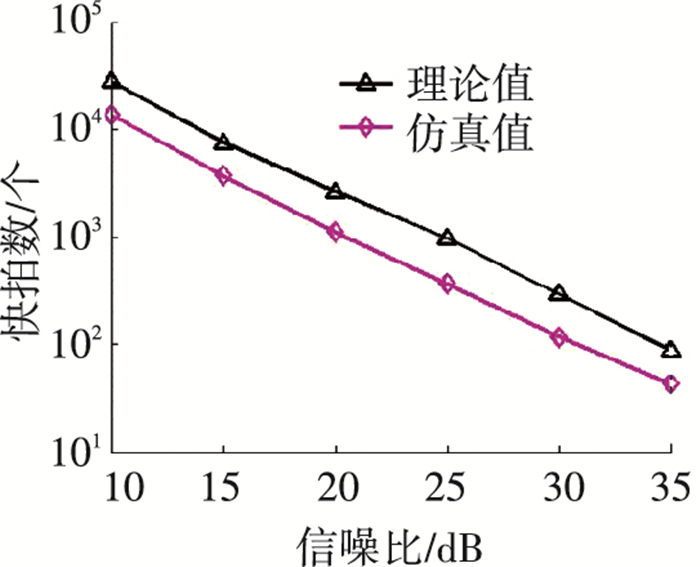
仿真中取图 2的柱面共形阵列, 其他仿真条件为:两个窄带独立信号入射, 参数分别为(θ1, ϕ1, γ1, η1)=(5°, 50°, 45°, 90°), (θ2, ϕ2, γ2, η2)= (7°, 52°, 47°, 92°), 信噪比从10 dB变换到35 dB, 由式(48)可计算出不同信噪比下分辨力门限的理论值; 在不同信噪比条件下, 独立实验200次, 定义成功分辨概率>90%时对应的快拍数为分辨力门限, 可得分辨力门限的仿真值, 最终得到仿真结果见图 4.
|
图 4 柱面共形阵列分辨力门限 |
由图 4可看出, 分辨力门限的理论值表现为随着信噪比的增加, 快拍数门限大致成指数规律下降; 分辨力门限的仿真值与理论值的下降趋势基本一致, 且仿真值低于理论值.产生该结果的原因有以下两点: 1)在分辨力门限推导过程中采取了两次近似(式(44)、(45), 以及式(47)、(48)的近似处理); 2)仿真中给出的分辨力门限是指分辨成功率达到90%时所对应的快拍数, 低于理论上成功分辨率为100%所需的快拍数.综上, 图 4所示的仿真结果证明了本文方法的正确性.
仿真实验3:考察球面共形阵列与均匀圆阵在分辨力性能上的差异.
仿真中取双极化球面共形阵列见图 5, 具体参数为:圆环阵个数3, 由上至下每个圆环分布的阵元数为4、8、12, 阵元之间均匀分布.球面的半径为3λ, 圆环阵之间的高度为λ.仿真中取双极化均匀圆阵参数为:圆阵半径3λ, 双极化阵元个数为24个, 均匀分布在圆周上.

|
图 5 双极化球面共形阵列示意 |
仿真条件:两个窄带独立信号入射, 参数分别为(θ1, ϕ1, γ1, η1)=(60°, 100°, 80°, 100°), (θ2, ϕ2, γ2, η2)= (64°, 100°, 80°, 100°), 快拍数为200, 信噪比从0 dB变化到30 dB, 独立实验200次, 统计分辨成功概率, 可得仿真结果见图 6.

|
图 6 双极化球面共形阵列与均匀圆阵分辨成功率 |
由图 6所示仿真结果可看出, 对于球面共形阵列而言, 在信噪比达到6 dB时成功分辨率即达到100%;而均匀圆阵达到100%的成功分辨率需要的信噪比为24 dB.产生以上结果的原因是, 共形阵列可以充分利用载体的立体孔径, 在入射角θ较大时, 其有效孔径基本不变; 而平面布阵的均匀圆阵在入射角θ较大时, 其有效孔径变得较小; 两种阵列在有效孔径的变化使其分辨力性能表现出较大差异.
5 结论本文首先建立了单极化和双极化共形阵列信号模型; 在此基础上通过MUSIC零谱、期望谱以及噪声投影矩阵期望的定义, 推导了共形阵列的理论分辨力门限; 最后通过计算机仿真研究了分辨力门限理论值与实际值的关系, 结果表明, 由仿真和理论分析得到共形阵列快拍数门限, 均随着信噪比的增加逐渐下降, 证明了理论分析的正确性; 同时, 共形阵列与平面阵列的分辨力仿真结果表明, 共形阵列可以充分利用载体的纵向孔径, 提高系统的分辨力性能.本文方法仅针对理想情况进行讨论, 当阵列存在幅相误差时如何得到分辨力门限的理论值, 还需进一步的研究.
| [1] |
ABBASPOUR M, HASSANI H R. Wideband planar patch antenna array on cylindrical surface[J]. IEEE Antennas and Wireless Propagation Letters, 2009, 8: 394-397. DOI:10.1109/LAWP.2009.2014889 |
| [2] |
GIAMPIERO G, LEONARDO Z. Multilayer array antennas with integrated frequency selective surfaces conformal to a circular cylindrical surface[J]. IEEE Trans on Antennas and Propagation, 2005, 53(6): 2020-2030. DOI:10.1109/TAP.2005.848459 |
| [3] |
LI Wentao, SHI Xiaowei, Hei Yongqiang, et al. A hybrid optimization algorithm and its application for conformal array pattern synthesis[J]. IEEE Trans on Antennas and Propagation, 2010, 50(10): 3401-3406. |
| [4] |
王布宏, 郭英, 王永良. 共形天线阵列流形的建模方法[J]. 电子学报, 2009, 37(3): 481-484. |
| [5] |
齐子森, 郭英, 王布宏. 共形阵列天线MUSIC算法性能分析[J]. 电子与信息学报, 2008, 30(11): 2674-2677. |
| [6] |
张树银, 郭英, 齐子森, 等. 锥面共形阵列相关源DOA和极化参数的联合估计算法[J]. 宇航学报, 2012, 33(7): 956-963. |
| [7] |
杨鹏, 杨峰, 聂在平, 等. 基于圆柱共形阵的快速来波方向估计[J]. 电波科学学报, 2012, 27(1): 61-65. |
| [8] |
QI Zisen., GUO Ying, WANG Buhong. Blind direction of arrival estimation angorithm for conformal array antenna with respect to polarization diversity[J]. IET Microwaves, Antennas & Propagation, 2011, 5(4): 433-442. |
| [9] |
张树银, 郭英, 齐子森, 苏令华. 基于子空间原理的共形阵列多参数联合估计算法[J]. 系统工程与电子技术, 2012, 34(6): 1146-1152. |
| [10] |
张树银, 郭英, 齐子森, 霍文俊. 共形阵列LFM信号多参数估计的传播算子算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(4): 181-187. |
| [11] |
张学敬, 杨志伟, 廖桂生. 共形阵列幅相误差校正快速算法[J]. 电子与信息学报, 2014, 36(5): 1100-1105. |
| [12] |
司伟建, 万良田, 刘鲁涛, 等. 共形阵列天线超宽频带波达方向实时估计[J]. 哈尔滨工程大学学报, 2014, 35(7): 913-918. |
| [13] |
徐艳红, 史小卫, 许京伟, 李平. 基于响应矢量优化的共形阵列稳健波束形成方法[J]. 电子与信息学报, 2014, 36(9): 2220-2226. |
| [14] |
王永良, 陈辉, 彭应宁, 万群. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 90-92.
|
| [15] |
LEE H.B., WENGROCITZ M.S. Resolution Threshold of Beamspace MUSIC For Two closely spaced emitters[J]. IEEE Trans. on Acoustics Speech and Signal Processing, 1990, 38(9): 1545-1559. DOI:10.1109/29.60074 |
 2016, Vol. 48
2016, Vol. 48


