由于高斯核产生的尺度空间能很好地模拟哺乳动物的视觉生物认知, 近年来, 多尺度理论逐渐成为视觉领域一个新兴的热点.在前人研究的基础上, Lowe与他的团队[1]提出SIFT算子.
SIFT算子被认为是综合性能最好的不变特征变换算子[2]并被国内外学者广泛应用在不同的领域.文献[3-4]运用该算子实现目标分类并应用在人脸识别领域; 文献[5]融合SIFT特征点与边缘信息很好地解决图像局域几何配准问题; 文献[6]将SIFT算子应用在医学影像光流场配准并取得很好的效果; 文献[7]则结合区域选择和SIFT算法很好地实现遥感图像配准.
针对SIFT算子时间复杂度过高、仿射不变性能不理想、复杂环境下误匹配过多等问题[8], 涌现多种改进算法.文献[9]提出的ASIFT(affine sift)算子在SIFT的基础上加入了相机的角度参数, 大大提高了算法的仿射不变性, 但时间复杂度成倍地增加; 文献[10]把压缩感知理论的稀疏特征表示概念引入SIFT算法中, 运算速度比传统SIFT算法和几种改进的SIFT算法有明显提高; 文献[11]采用包括SIFT在内的5种特征算子有效提高遥感图像场景分类的精度.
虽然采用不同的方式对SIFT算法进行改进, 但是与原算法一样, 都是通过遍历整个高斯尺度空间获得尺度不变性的, 因此这类算法存在两个问题, 一是算法复杂度比较高; 另一个问题就是遍历所有尺度会导致小尺度下特征点的抗噪声能力差, 在复杂环境下误匹配率会大大增加.本文将从尺度空间的本质出发, 提出一种基于因果关系的尺度不变特征提取算法, 在提高算法效率的同时增强抗噪能力.
1 高斯尺度空间的因果关系近年来Lindeberg的尺度空间理论引起学者普遍关注, 并在文献中给出尺度空间的规范定义, 理论证明, 尺度空间就是高斯尺度空间.
高斯尺度空间是图像与参数不同的高斯核卷积产生的一系列平滑图像, 见图 1.

|
图 1 Lena图像的尺度空间表示 |
因果关系是高斯尺度空间最重要的属性之一.在连续信号的平滑过程中表现在极值点不会增加, 而极值点的坐标发生漂移.
尺度空间的n阶导数为

|
(1) |
式(1)可看出, 尺度的增大不会增加极值点的数目但极值点的位置会随着g(·;t)的变化而变化.
定义1 如果将局部极值看作平滑度的一种度量, 那么随着尺度的增大, 尺度空间的极值是非增的且没有新的极值产生, 这种属性就称为“尺度空间的因果关系”.
推理1 如果信号f与尺度为σ1的高斯核卷积后得到尺度空间函数L1, 存在极值点(x1, y1), 则对于任意尺度σ < σ1, f与尺度为σ的高斯核卷积后得到尺度空间函数L一定存在与(x1, y1)对应的极值点(x, y).
证明 由因果关系的定义, 在尺度空间中随着尺度增大, 没有新的极值点产生, 因此, 如果小的尺度σ不存在极值点(x, y), 那么在大的尺度σ1下也不会有新的极值点(x1, y1).
推理2 如果在大尺度σ1下尺度空间函数L1存在极值点(x1, y1), 那么所有<σ1的尺度下的尺度空间函数L中均存在与之对应的极值点, 在某种意义上说, 极值点(x1, y1)在尺度[0, σ1]的范围内是尺度不变的.
推理3 理想情况下, 在图像的高斯尺度空间中, 在大尺度σ1下图像获得的特征点在小尺度上存在对应特征点, 在某种意义上说, 该特征点在尺度[0, σ1]的范围内是尺度不变的.
事实上, 由于在离散化过程中导致的量化误差, 因此图像领域内的这种因果关系并不是严格的满足.
2 本文方法 2.1 尺度不变特征提取推理3中给出图像中提取尺度不变特征点的一种方法, 只要在大的尺度上获得的特征点, 那么该特征点就是在该尺度下是尺度不变的.
设Xσ为在尺度σ下提取的特征点, ησ为在尺度σ下尺度不变特征点集合, 那么:
∀σ′ < σ如果满足Xσ∈ησ则∃ Xσ’ ∈ησ′.
按上面的推理, 在尺度空间中提取的特征会在不同的尺度上重复出现, 增加了算法的时间开销, 同时由于小尺度下抗噪能力差, 在噪声环境下有可能会出现误匹配.
然而, 随着尺度的增加, 这种特征点的位置会发生漂移, 因此还需要解决特征点精确位置的问题.
图 2是Lena图像在尺度为2.4的尺度空间图像中获得特征点以及在原图中对应的位置, 可以看出, 它们发生了较大的偏移.

|
图 2 尺度空间特征点漂移现象 |
本文提取的尺度不变特征点分为3个主要步骤:
1) 将尺度参数σ=1.3的高斯函数和与原图像f卷积获得高斯图像g;
2) 分别在原图像f与高斯图像g中提取Harris角点作为候选尺度不变特征点;
3) 在高斯图像g中, 遍历每一个Harris角点, 以该角点为中心, 向原图像f投影, 投影区域选择以r为半径的圆形区域.针对原图f上投影区域角点的数目分3种情况进行处理:投影区角点数为0, 则由于量化误差, 该特征点无效; 投影区角点数为1, 该点即为最终的尺度不变特征点; 投影区角点数>1, 分别计算投影区每个角点的h值, 选择与高斯图像g中对应的投影角点的h值最接近的一个作为最终的尺度不变特征点.
步骤3中的h值为Harris算子, 定义如下:
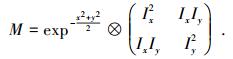
|
(2) |
式中:Ix=∂I/∂x, Iy=∂I/∂y.设M的特征值分别是λ1、λ2, Harris算子h为
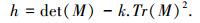
|
(3) |
式中:det(M)=λ1×λ2, Tr(M)=λ1+λ2, k为系数, k=0.04~0.06.
上述步骤中有两个重要的参数, 一个是高斯核的尺度参数, 该参数选择过大将导致图像的特征点太少, 选择过小又会造成抗噪以及尺度不变性能提高不明显.本文针对上百幅图像进行实验, 发现当σ=1.3时综合效果比较理想.另外一个参数是投影区域的投影半径, 参照SIFT算法给出的经验值, 选取半径为3倍尺度参数, 即4个像素点.

|
图 3 位置精确的尺度不变特征点提取示意图 |
尺度不变性要求图像在不同尺度下提取的特征点不发生变化, 图 4是结构化图像在不同的尺度下分别采用Harris算子、SIFT (DOG)算子以及本文推荐的算法所提取的特征点, 可看出, 无论从特征点的数目还是特征点的位置, 本文推荐的算法尺度不变性最好.

|
图 4 3种算法的尺度不变性比较 |
可以使用下面的公式测试不同算法的尺度不变性能:

|
(6) |
式中:R1, 2为在原图中的特征点与变化尺度后获得的特征点重复数量, S1, 2获得的特征点总数, R值表示重复率.本文针对65幅自然图像求取R值, 最后取平均值进行统计, 在不同尺度下重复率曲线见图 5.
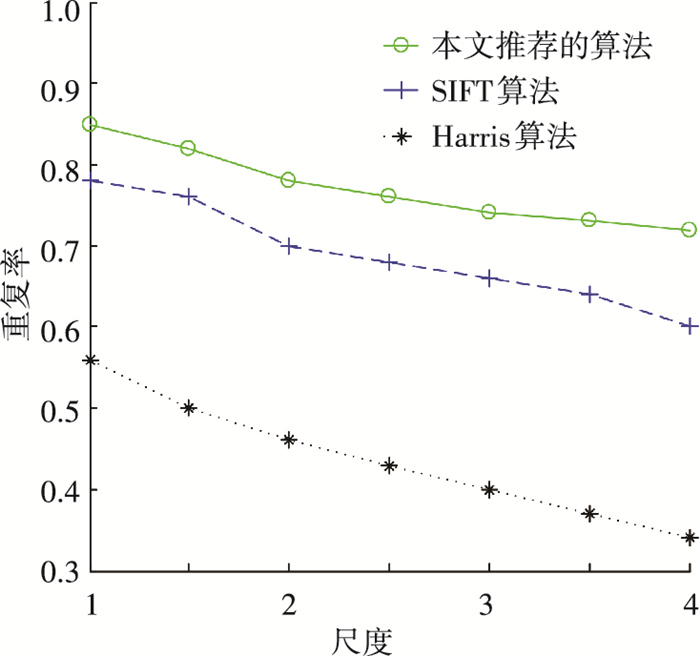
|
图 5 3种方法重复率与尺度之间的关系 |
由于只在大尺度下提取图像的特征点, 降低时间复杂度, 本文算法与SIFT算法提取特征点所消耗的时间比较见表 1.
| 表 1 算法时间比较 |
从表 1可看出, 本文推荐算法重复率优于SIFT算法, 计算效率也大大优于后者, 而且随尺度增加, 特征点个数减少, 所消耗的时间也随之下降.另外, 本文推荐的算法是基于Harris算子的, 因此也具备Harris算子的旋转不变性与平移不变性, 其中旋转不变性效果见图 6.

|
图 6 本文算法的旋转不变性 |
本文推荐的算法是在大尺度下提取的特征点, 因此具有较强的抗噪能力.图 7是在增加椒盐噪声情况下提取特征点的效果, 最左边的图像是3种算法对原图的特征点提取效果, 中间的图像为增加参数为0.01的椒盐噪声提取的特征点效果, 最右侧的图像为增加参数为0.02的椒盐噪声提取的特征点效果, 效果显示, Harris的抗噪能力极差, SIFT算子的抗噪能力较好, 本文推荐的算法抗噪效果最好.

|
图 7 非结构目标特征提取效果比较 |
在复杂的环境下, 如海底, 往往存在许多噪声.机器人在海底实现对目标的定位抓取是目前海底视觉应用的一个热点, 而获得稳定特征点是实现海底目标定位的关键.图 8(a)是一幅海底矿物图像, 从图中可发现存在许多的浮游生物与海底灰尘对图像造成干扰.分别采用Harris算子, SIFT算子以及本文推荐的算子提取目标特征点, 获得的效果见图 8(b)~(d).

|
图 8 海底图像特征提取 |
在实验室环境下, Harris算子耗时0.265 0 s, 提取748个特征点; SIFT算子耗时37.59 s, 提取563个特征点; 本文推荐的算法提取163个特征点, 耗时0.854 3 s.从提取效果看, 本文推荐算法提取的特征点最稳定; 从实验数据看, 本文推荐算法在时间上接近Harris算子.因此在复杂的环境下, 本文推荐的算法综合性能最好, 虽然提取的特征点数目不多, 但是许多情况下并不需要太多的特征点数目, 如基于双目视觉的目标定位与三维重建等.
本文所有实验均在以下环境下进行:
操作系统为Windows XP, CPU为酷睿i5,内存为2 G.
4 结论目前的尺度不变特征提取大多是基于尺度空间的, 典型的如SIFT算法族, 由此带来了算法复杂, 抗噪能力不强等弊端.本文提出尺度不变特征提取算法从高斯尺度的因果关系出发, 采用从上向下投影的方法实现像素点坐标的精确定位.实验结果证明, 本文推荐的算法具有较低的时间复杂度与较强的抗噪能力.适合对算法实时性比较高而对特征点提取数量要求不高的复杂环境, 如在线全景图像拼接, 基于8点基本矩阵的实时目标定位与三维目标重建等.
虽然本文算法提出了一种可靠的尺度不变特征提取算法, 但是由于没有遍历整个尺度, 因此要实现机器视觉的后续相关任务还需要获得图像的局部特征尺度, 特征尺度可以用来表征特征点的邻域独特性, 根据视觉理论, 也就是区域的不可预见性.目前已有许多成熟的算法, 如T Kadir提出的基于熵极值法等, 但这些算法大多基于各向同性的算子, 会导致仿射不变性较差.如何找到高效的各向异性局部特征尺度算子是本文下一步工作的重点.
| [1] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [2] |
JUAN L, GWUN O, JUAN L, et al. A Comparison of SIFT, PCA-SIFT and SURF[J]. International Journal of Image Processing, 2009(4): 143-152. |
| [3] |
SANCHO M, LOWE D G. Local naive bayes nearest neighbor for image classification[C]//Proceedings of Computer Vision and Pattern Recognition (CVPR) 2012. Rhode Island, USA: IEEE, 2012: 3650-3656. http://dl.acm.org/citation.cfm?id=2354695
|
| [4] |
KRIZAJ J, STRUC V, PAVESIC N. Adaptation of SIFT features for face recognition under varying illumination[C]//Proceedings of the 33rd International Convention 2010. Opatija, Croatia: IEEE, 2010: 691-694. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5533495
|
| [5] |
孙统风, 丁世飞. 基于改进尺度不变特征的图像局域几何配准研究[J]. 计算机科学, 2014, 41(1): 111-115. |
| [6] |
于文勇, 康晓东, 葛文杰, 等. 结合拓扑纹理图像局部不变特征的医学影像光流场配准[J]. 计算机应用, 2014(S1): 206-210. |
| [7] |
樊东昊, 朱建军, 郭南男, 等. 一种结合区域选择和SIFT算法的遥感图像配准方法准[J]. 工程勘察, 2015, 43(2): 69-74. |
| [8] |
刘立, 詹茵茵, 罗扬, 刘朝晖, 彭复员. 尺度不变特征变换算子综述[J]. 中国图象图形学报, 2013, 18(8): 885-892. DOI:10.11834/jig.20130801 |
| [9] |
MOREL J, YU G. ASIFT:A New framework for fully affine invariant image comparison[J]. Siam Journal on Imaging Sciences, 2009, 2(2): 438-469. DOI:10.1137/080732730 |
| [10] |
杨飒, 杨春玲. 基于压缩感知与尺度不变特征变换的图像配准算法[J]. 光学学报, 2014, 34(11): 1-5. |
| [11] |
徐侃, 陈丽君, 杨文, 等. 利用特征选择的遥感图像场景分类[J]. 哈尔滨工业大学学报, 2011, 43(9): 117-121. DOI:10.11918/j.issn.0367-6234.2011.09.023 |
 2016, Vol. 48
2016, Vol. 48



