算术编码AC(arithmetic coding)是一种压缩效率比Huffman编码更高的熵编码, 因其良好的压缩性能成为无损压缩的主流, 被广泛应用于各种多媒体压缩标准中, 例如H.264、JPEG2000等.随着AC理论研究的逐渐深入, 其安全性也越来越受到诸多学者的关注.文献[1]提出自适应算术编码具有较好的加密效果, 因其在编码过程中产生了相对随机的编码区间.文献[2]分析指出自适应算术编码不能抵抗选择性明文攻击.因此, 为提高传统算术编码TAC(traditional arithmetic coding)的安全性, 有必要对其编码方法进行修改.
文献[3]最早提出了二元随机算术编码BRAC(binary random arithmetic coding)的思想.文献[4]将BRAC与混沌系统相结合实现加密, 但损失6%左右的压缩效率.文献[5-8]在BRAC过程中引入混沌映射模型, 利用混沌映射生成加密密钥, 增加密钥的破译难度.但从文献[5]可看出, 当用错误密钥译码时, BRAC得到的误符号率SER(symbol error rate)不超过50%.换言之, 当用错误密钥解密截获的密文时, 能获取明文中一半以上的信息, 所以BRAC对密文攻击抵抗力较弱.文献[9-11]提出区间分割算术编码, 该方法拥有较好的加密效果, 但其实现复杂度高, 并且牺牲了部分压缩效率.文献[12]提出的安全算术编码采用一阶Markov信源模型, 但其在编码过程中需要保存不同条件概率下的编码区间, 将占用较多存储空间.
为进一步提高TAC的安全性, 提出一种基于多元符号的安全算术编码M-SAC(M-ary security arithmetic coding).M-SAC在编码过程中利用密钥对多元符号在编码区间中的位置进行循环移位, 增加了编码区间分割的随机性.
1 传统算术编码算术编码的概念最早由Elias提出, 其核心思想是:从整个符号序列出发, 按照符号输入的顺序将符号的概率进行累积, 最终把符号序列映射为[0, 1)区间内的一个点.由于在编码过程中引入了小数, AC具有很高的压缩效率.文献[13-14]对其理论研究, AC已成为一种实际可行的熵编码.相互独立的概率统计模块和编码模块组成的AC比其它熵编码更加灵活.
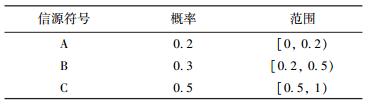
概率统计模块包括两种模型:静态模型和自适应模型.静态模型是指在编码过程中符号概率一直不变; 自适应模型是指符号概率随着编码过程而改变.为简化分析, 本文讨论静态模型下AC的编码原理.设信源由3个符号{A, B, C}组成, 其概率和范围见表 1.
| 表 1 信源符号概率和范围 |
从编码区间的下界到上界, 将信源符号出现的顺序称之为信源符号在编码区间中的位置.设输入符号序列为“BACBC”, 信源符号在编码区间中的位置为“ABC”, 静态TAC编码过程见图 1.编码的初始区间为[0, 1).当输入第一个符号“B”过后, 编码区间缩小为“B”对应的范围[0.2, 0.5).同时, 将区间[0.2, 0.5)按照符号在编码区间中的位置和概率进行分割, 为编码下一个符号做准备.编码下一个符号时, 区间进一步缩小为其对应的范围, 再进行分割, 如此循环, 直到编码完最后一个符号.从图 1可看出, 对符号序列“BACBC”进行编码最终得到的编码区间为[0.2405, 0.245), 在该区间内任取一点可作为编码码字.

|
图 1 静态TAC编码过程 |
译码时, 根据码字所在区间对应的信源符号来进行译码, 译码区间的分割与编码相同.自适应TAC与静态TAC唯一的区别是其在编码过程中有符号概率的更新.
2 安全算术编码 2.1 编码理论从图 1中可看出, 在整个编码过程中信源符号在编码区间中的位置均未改变, 这使得TAC不能抵抗选择性明文攻击[2].本文提出的M-SAC很好地解决了这个问题.与TAC的本质区别在于:该方案先利用加密向量改变信源符号在编码区间中的位置, 再用TAC进行编码, 这样就将数据压缩和加密结合在一起, 译码时完全依赖于密钥才能正确译码.
加密向量是通过种子生成的与输入符号序列长度相等的二进制序列, 密钥是加密向量中的其中一位.当密钥为1时, 将信源符号在编码区间中的位置进行循环右移(或左移); 当密钥为0时, 位置不变.
同样以编码符号序列“BACBC”为例.设信源符号在编码区间中的初始位置为“ABC”, 循环移位的方向为右移, 加密向量为“01101”.
静态M-SAC编码过程见图 2.经过加密后, 信源符号在编码区间中的位置发生了变化.编码结束时, 得到的编码区间为[0.372 5, 0.377), 与图 1中TAC得到的编码区间不同, 因此得到的编码码字也不同.若想正确译码, 必须知道加密向量, 否则译码失败.
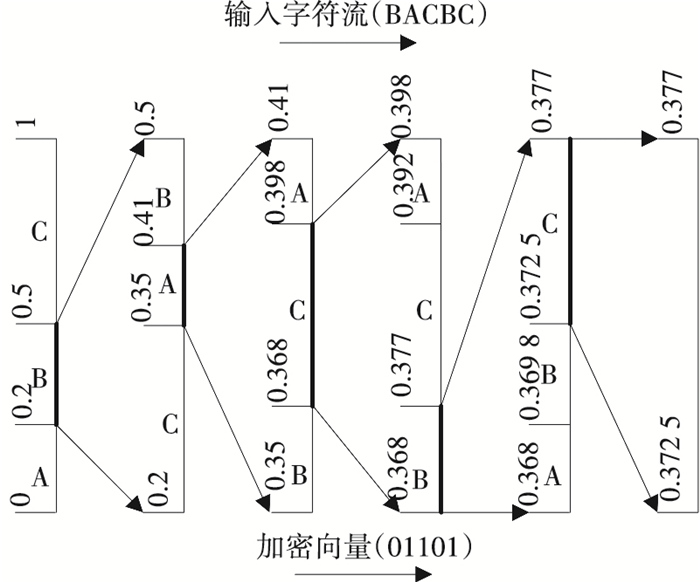
|
图 2 静态M-SAC编码过程 |
K为加密向量, ki为第i个加密密钥, 在静态模型下, M-SAC编/译码步骤为:
1) 用种子生成加密向量K;
2) 令i=0, 初始化信源符号在编/译码区间中的位置, 设置循环移位的方向;
3) 如果ki=1, 先将信源符号在编/译码区间中的位置进行循环移位, 再用TAC进行编/译码; 如果ki=0, 直接用TAC进行编/译码;
4) i增加1, 更新ki;
5) 返回到3), 直到编/译码结束.
在自适应模型下, 只需在第3、4步之间更新信源符号的概率.
2.2 压缩效率信息论[15]指出对任何一个独立无记忆信源进行编码, 编码一个符号所需的平均比特数不低于该信源的香农熵.对于三元信源, 设pA、pB和pC分别为信源符号“A”、“B”和“C”的概率, 则香农熵为
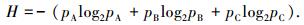
|
(1) |
设S=(s1, s2, …, sN)表示长度为N的符号序列.根据AC理论, 编码这N个符号需要的比特数为l=-log2(p), 其中

|
(2) |
设编码这N个符号所需的实际比特数超过理论值的上限为ε, 于是实际编码每个符号需要的平均比特数HS应满足: HS≤[(ε+l)/N], 结合式(2)可得

|
(3) |
设符号序列中“A”的个数为NA, “B”的个数为NB, “C”的个数为NC, 即满足N=NA+NB+NC.当N∞时有: pA=NA/N, pB=NB/N, pC=NC/N.编码每个符号所需比特数的期望值为
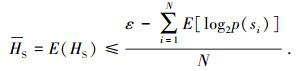
|
(4) |
其中

|
(5) |
式(4)可化为

|
(6) |
又编码每个符号所需的比特数不小于香农熵, 则HS满足

|
(7) |
所以当N→∞时, 有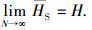
推导可知:当N足够大时, M-SAC编码一个符号所需的比特数等于该信源的香农熵, 能获得最优的压缩效率.同时, 对比图 1、2的编码过程可发现, 最终得到的编码区间不同, 但编码区间的长度是相等的, 因此M-SAC对TAC的压缩效率没有影响.
2.3 安全性M-SAC利用加密向量改变信源符号在编码区间中的位置, 使编码区间分割与密钥相关联, 提高了TAC对选择性明文攻击的抵抗力.同时, 编码前设定的信源符号在编码区间中的初始位置和循环移位的方向也是一种加密.因此, 对于密文攻击, 若不知道信源符号在编码区间中的初始位置、循环移位的方向和加密向量, 将无法正确译码.因此M-SAC能有效抵抗密文和选择性明文攻击, 安全性非常高.
3 仿真分析仿真中采用独立无记忆的三符号信源, 输入符号序列的长度为10 000, 信源符号在编码区间中的初始位置为“ABC”, 循环移位的方向为右移.
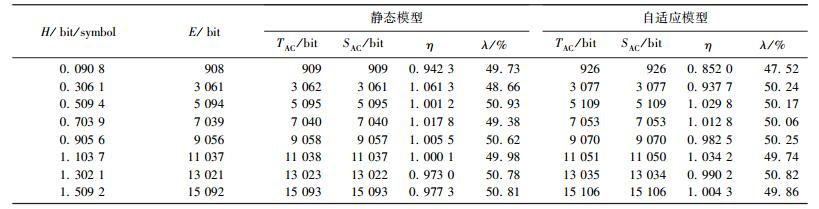
3.1 压缩效率选择8种信源, 在静态和自适应模型下比较TAC和M-SAC的压缩效率, 仿真结果见表 2.其中H为信源的香农熵; E为熵编码界(编码输入符号序列所需比特数的下限), E=N×H=10 000 H; TAC为用TAC输出的比特数; SAC为用M-SAC输出的比特数; η为M-SAC输出的二进制序列中1与0的个数比; λ为M-SAC输出序列相对于TAC输出序列的变化率.
| 表 2 TAC与M-SAC的压缩效率 |
从表 2中可看出, 当信源香农熵和概率模型一定时, M-SAC与TAC输出的比特数相等或相差1.这是因为AC具体实现时精度有限, 在编码过程中改变信源符号在编码区间中的位置, 会导致输出的比特数与TAC相比有1 bit左右的差值.由此可得, M-SAC对TAC的压缩效率没有影响.而文献[4, 9]中提出的安全算术编码方案损失了部分压缩效率, 文献[4]中损失的压缩效率达到6%.
同时在两种概率模型下, M-SAC输出的二进制序列中1与0的个数比都在1左右, 说明密文中“1”和“0”的个数相对平衡, 达到了理想的加密效果.从λ值可知, M-SAC输出序列相对于TAC输出序列的变化率在50%左右, 说明经过加密编码输出序列变化随机性强, 安全性高.
3.2 密钥敏感性对于二进制密文, 如果改变加密向量中某一位或某几位, 密文的变化率达到50%, 说明加密向量敏感性强.
图 3为当信源香农熵为1.302 1 bit/symbol时, 改变加密向量, 在不同种子和概率模型下M-SAC得到的密文的变化率.可看出, 对于不同的种子和概率模型, 无论改变多少个加密密钥, 密文的变化率都在50%左右, 所以加密向量具有很强的敏感性.

|
图 3 改变加密向量密文的变化率 |
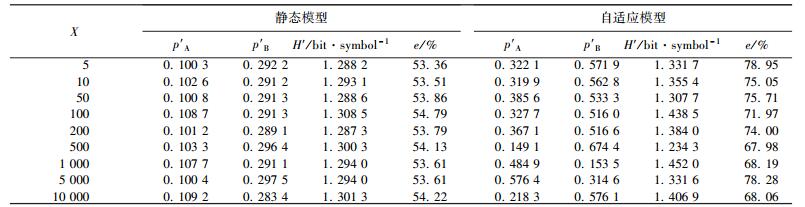
表 3为在两种概率模型下, 当信源的香农熵为1.302 1 bit/symbol(pA=0.105 0、pB=0.294 0)时, 解密向量的敏感性.其中X为改变解密密钥的个数, H′和e分别为译码符号序列的香农熵和SER, p′A和p′B分别为译码符号序列中“A”和“B”的概率.
| 表 3 解密向量的敏感性 |
从表 3可看出, 在两种概率模型下, 改变解密向量, 译码符号序列的p′A、p′B和H′与输入符号序列相比都发生了改变, SER超过50%.在自适应模型下, SER甚至接近80%.改变解密密钥的个数对SER没有太大影响, 说明解密向量敏感性强.
为比较两种概率模型的加密安全性, 表 4给出了在静态模型和自适应模型下, 针对不同的信源, 运用错误密钥(与加密向量有10位不同)解码, 得到的译码序列的香农熵(H′)和SER(e), 及译码序列中符号“A”和“B”的概率p′A和p′B.其中pA和pB分别为输入序列中符号“A”和“B”的概率.
| 表 4 不同信源的加密安全性 |
表 4表明在静态模型下译码序列中符号“A”和“B”的概率与输入序列中对应符号的概率非常相近; 而在自适应模型下, 译码序列中符号的概率与输入序列中对应符号的概率相比发生了很大变化.同时, 在静态模型下SER随信源熵增加而增大, 但都小于自适应模型下的SER.另外, 自适应模型下H′的改变程度比在静态模型下更大.由此可知, 自适应模型比静态模型加密安全性更高, 更难破译.这是因为在自适应模型下符号的概率随编码过程不断地更新; 而在静态模型下, 符号的概率在编码过程中一直不变.
当用错误密钥译码时, 与文献[5]中的BRAC相比, M-SAC得到的SER更高, 尤其是在自适应模型下.故M-SAC的加密效果更好, 对密文的抵抗力更强.
3.3 明文敏感性明文敏感性是指改变明文中的某一位或某几位, 密文的变化情况.当信源熵为1.302 1 bit·symbol-1时, 改变明文, 在不同种子和概率模型下M-SAC得到的密文的变化率见图 4.

|
图 4 改变明文密文的变化率 |
图 4表明对于不同的种子和概率模型, 当改变明文中2~50个符号时, 密文的变化率在41%~50%.也就是说, 明文稍微改变就会引起密文的随机变化, 说明明文敏感性较强.
4 结论本文提出基于多元符号的安全算术编码, 将数据压缩和加密结合在一起.利用密钥对信源符号在编码区间中的位置进行循环移位, 改变AC的编码区间, 进而改变编码码字.理论分析M-SAC的压缩效率和安全性.仿真表明, 当利用错误密钥译码时, 在自适应模型下, M-SAC能得到70%以上的BER, 比BRAC加密效果更好.同时, M-SAC对压缩效率没有影响, 并且具有很强的密钥敏感性和明文敏感性, 对密文和选择性明文攻击有很强的抵抗力.讨论三元符号的安全算术编码, 更高元的安全算术编码方法与其类似.随着编码元数的增加, M-SAC的安全性会更高, 但其复杂度也会上升.在实际应用中, 平衡加密安全性和复杂度, 选择合适的编码元数.该方案可应用于对密文攻击抵抗力要求高的系统中.
| [1] |
WITTEN I H, CLEARY J G. On the privacy afforded by adaptive text compression[J]. Computer Security, 1988, 7: 397-408. DOI:10.1016/0167-4048(88)90580-9 |
| [2] |
BERGEN H A, HOGAN J M. A chosen plaintext attack on an adaptive arithmetic coding compression algorithm[J]. Computer Security, 1993, 12: 157-167. DOI:10.1016/0167-4048(93)90099-Q |
| [3] |
GRANGETTO M, MAGLI E, OLMO G. Multimedia selective encryption by means of randomized arithmetic coding[J]. IEEE Transactions on Multimedia, 2006, 8(5): 905-917. DOI:10.1109/TMM.2006.879919 |
| [4] |
BOSE R, PATHAK S. A novel compression and encryption scheme using variable model arithmetic coding and coupled chaotic system[J]. IEEE Transactions on Circuits and Systems, 2006, 53(4): 848-857. DOI:10.1109/TCSI.2005.859617 |
| [5] |
LI Hengjian, ZHANG Jiashu. A secure and efficient entropy coding based on arithmetic coding[J]. Communications on Nonlinear Science and Numerical Simulation, 2009, 14: 4304-4318. DOI:10.1016/j.cnsns.2009.03.003 |
| [6] |
WONG K, LIN Qiuzhen, CHEN Jianyong. Simultaneous arithmetic coding and encryption using chaotic maps[J]. IEEE Transactions on Circuits and Systems, 2010, 57(2): 146-150. |
| [7] |
代才莉, 包万宇. Logistic映射控制的安全算术编码及其在图像加密中的应用[J]. 重庆大学学报, 2012, 35(8): 87-91. DOI:10.11835/j.issn.1000-582X.2012.08.015 |
| [8] |
王小龙, 赵庶旭. 基于分段线性混沌映射的算术编码与加密[J]. 计算机应用研究, 2014, 31(5): 1481-1483. |
| [9] |
WEN Jiangtao, KIM H, VILLASENOR J D. Binary arithmetic coding with key-based interval splitting[J]. IEEE Signal Processing Letters, 2006, 13(2): 69-72. DOI:10.1109/LSP.2005.861589 |
| [10] |
KIM H, WEN Jiangtao, VILLASENOR J D. Secure arithmetic coding[J]. IEEE Transactions on Signal Processing, 2007, 55(5): 2263-2272. DOI:10.1109/TSP.2007.892710 |
| [11] |
ZHOU Jiantao, AU O C, WONG P H. Adaptive chosen-ciphertext attack on secure arithmetic coding[J]. IEEE Transactions on Signal Processing, 2009, 57(5): 1825-1838. DOI:10.1109/TSP.2009.2013901 |
| [12] |
DUAN Lili, LIAO Xiaofeng, XIANG Tao. A secure arithmetic coding based on Markov model[J]. Communications on Nonlinear Science and Numerical Simulation, 2011, 16: 2554-2562. DOI:10.1016/j.cnsns.2010.09.012 |
| [13] |
RISSANEN J, LANGDON G G. Arithmetic Coding[J]. IBM Journal of Research and Development, 1979, 23(2): 149-162. DOI:10.1147/rd.232.0149 |
| [14] |
WITTEN I H, NEAL R M, CLEARY J G. Arithmetic coding for data compression[J]. Communications of the ACM, 1987, 30(6): 520-540. DOI:10.1145/214762.214771 |
| [15] |
SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27: 379-423, 623-656. DOI:10.1002/bltj.1948.27.issue-3 |
 2016, Vol. 48
2016, Vol. 48