2. 中国科学院声学研究所, 100190 北京;
3. 水声对抗重点实验室(91388部队), 524022 广东 湛江
2. Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China;
3. Science and Technology on Underwater Acoustic Antagonizing Laboratory, No. 91388 Unit of PLA, 524022 Zhanjiang, Guangdong, China
水声信道环境复杂,表现为严重的多径时延、带宽受限、时变和多普勒频移等.其中,多径时延一般最大可达几个毫秒,甚至几十个毫秒,从而造成码间干扰比较严重.而1 500 m/s的水声传播速度远小于电磁波传播速度,从而造成多普勒频移比较严重.水声信道的复杂性给水下通信带来严重挑战.因此,如何对抗多径传播和多普勒频移一直是水声通信研究的热点.
目前,水声通信中主要应用两种机制:多载波正交频分复用OFDM(orthogonal frequency division multiplexing) [1]与单载波频域均衡SC-FDE(single carrier-frequency domain equalization)[2].OFDM系统主要用于克服多径传输,且频谱利用率高[3],但存在高峰均比和对频偏敏感等问题[4];SC-FDE系统能够降低峰均比,对频偏不敏感,但频谱利用率低[5].可见,OFDM和SC-FDE各有优缺点.
本文提出一种基于WFRFT的混合载波系统.它只需一套物理层传输设备就可实现单/多载波系统以及分数域系统,是一种真正意义上的混合载波调制系统[6].他可与现有的传输体制相兼容,也可在各分数域系统间平滑过渡,能与实际信道相匹配.WFRFT系统作为一种将单/多载波结合的传输手段尚未受到广泛研究,它在不同传输环境下的最优化传输也未发现相关文献.本文将在水声信道典型的多径和多普勒环境下,研究基于WFRFT的混合载波通信系统性能,并提出该系统最优阶的选取方法.
1 加权类傅里叶变换基本理论 1.1 加权分数傅里叶变换[7]的定义传统傅里叶变换的周期为4,令g(x)为满足均方可积的时域信号,对它连续做4次傅里叶变换
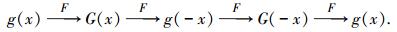
|
式中: G(x)为信号频域形式,g(-x)和G(-x)分别为信号时域和频域形式的反转, 变换阶次为α的4-WFRFT的具体表达式[8]为

|
(1) |
式中:wl(α)为加权系数.g(x)和g(-x)是时域信号;G(x)、G(-x)分别是g(x)、g(-x)经过傅里叶变换后的频域信号.wl(α)与α的数学关系为
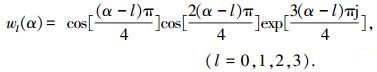
|
(2) |
式中α的周期为4,一般将区间[0, 4]定义为α的主周期.
传统傅里叶变换将时域信号由时域轴逆时针旋转π/2到频域轴.时域信号和频域信号在时频域平面上是正交的.
1.2 加权分数傅里叶变换的物理实现离散序列的反转操作(以g(-m)为例)为

|
(3) |
WFRFT可用FFT实现,从而降低实现的复杂度.具体实现见图 1系统结构[6].

|
图 1 基于FFT的WFRFT系统实现结构 |
由图 1可见,一次WFRFT只需进行一次相同长度的FFT运算,从乘法次数角度,两者的复杂度基本处于同一数量级上.WFRFT只是在加权过程中多了4N次乘法运算.因此,WFRFT算法在硬件上可实现.
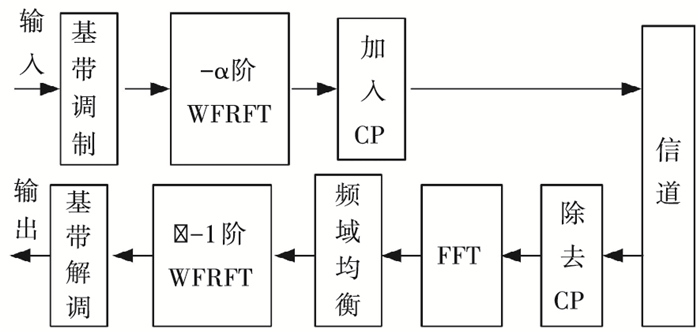
2 基于WFRFT的混合载波通信系统将WFRFT引入通信系统,并利用WFRFT的边界性和可加性构建混合载波系统[9], 见图 2.WFRFT的边界性即时域信号g(x)的0阶变换结果为信号时域形式,α=1时为信号频域形式;可加性可描述为
|
图 2 基于WFRFT的混合载波系统框图 |

|
(4) |
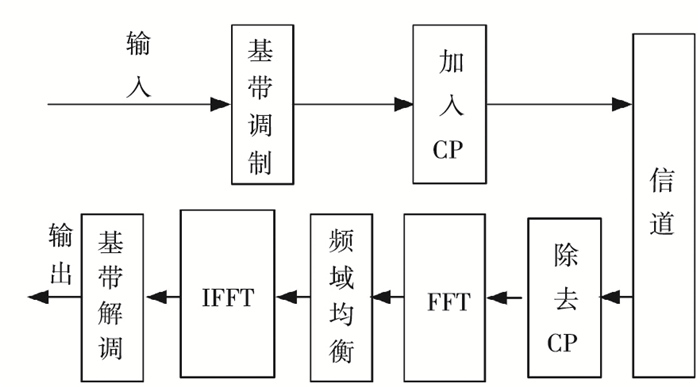
输入信号是由α阶分数域变换到时域,接收信号先经过FFT变换到频域进行均衡后,再经过(α-1)的WFRFT变换回α阶分数域.混合系统在取特定参数时可转化为现有的单/多载波系统.当α=0时,混合系统为SC-FDE系统见图 3;当α=1时,对应OFDM系统[10]见图 4.
|
图 3 SC-FDE的基本系统框图 |

|
图 4 基于FFT的OFDM系统实现框图 |
在不同环境下,通信系统的性能会差别很大,多径和多普勒的影响也会非常明显.因此在不同环境下,如何设计最优系统和求得系统最优解,对于提升WFRFT系统的性能,具有重要意义.
最佳通信系统是与信道不同传输条件紧密结合的.一般情况下,通信系统是以误比特率作为系统性能的衡量标准.

|
(5) |
式中: biterr为传输中错误比特数,bitall为传输的总比特数.
考虑到信号传输会受到通信环境中各种干扰的影响,而不同变换阶次下系统受这些干扰影响的程度也不同.干扰程度越小,对应误比特率也越小.因此结合变换阶次,设计系统优化目标,实现最优的WFRFT系统设计.
主要考虑多径和多普勒这两个因素,水声信道的冲激响应为
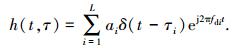
|
(6) |
式中: L, ai, τi, fdi分别为多径数、幅度、时延、多普勒频移.
源信号x(t)经过信道传输后,接收信号y(t)为

|
(7) |
式中:n(t)为高斯白噪声信号, 当采样频率为Fs时,接收信号的离散表示形式为
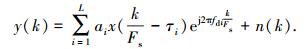
|
(8) |
接收信号y(k)包含了源信号x(k)信息以及多径、多普勒和噪声造成的干扰信息d(k).可用另一种表达形式:
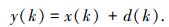
|
(9) |
在通信系统中,接收端接收信号后还要经过解调和判决,d(k)的大小会影响信号最终的正确判决,从而影响系统性能.而WFRFT系统中,选择不同的变换阶次,信号经过信道所受到的干扰程度也不同.令x=(x(1), x(2), …), y=(y(1), y(2), …),则在WFRFT系统中

|
(10) |
Nα越小,即干扰信息对源信号的影响越小,系统误比特率越小,系统性能更好.因此,以Nα的最小值为优化目标,在α主周期内进行搜索,当Nα最小时对应的α即为最优阶.最优阶选取问题的解可描述为

|
(11) |
式中:‖·‖2为2-范数,Fα[·]为α阶WFRFT.算法具体流程见图 5.
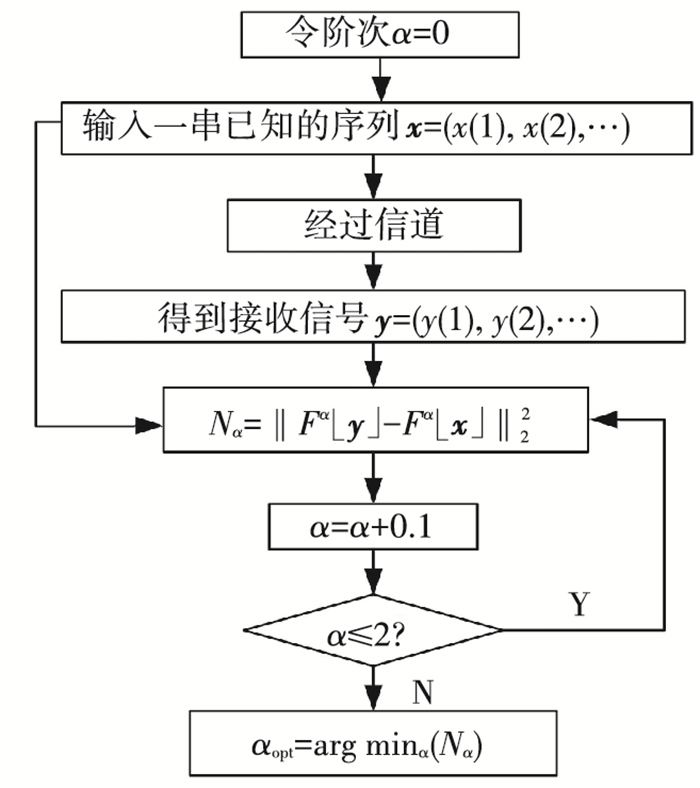
|
图 5 最优阶选取算法流程 |
将最优阶选取算法引入图 2所示系统中,得到的系统结构图见图 6.
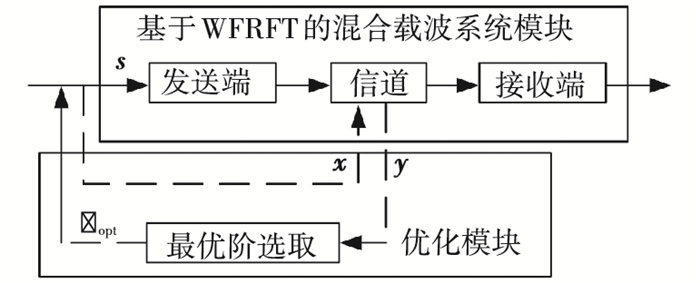
|
图 6 引入最优阶选取算法的WFRFT系统 |
在发送信号s前,先发送一串具有和s相同长度及结构的已知序列x.y为接收信号.根据图 5所示算法,选取最优阶αopt.将αopt反馈回发送端,再发送s.此时,基于WFRFT的混合载波系统是在αopt模式下通信的,系统误比特率最低,性能最好.
4 仿真和水池实验 4.1 仿真考虑到水声环境多径时延严重,在多径信道下进行了仿真.当多普勒频移为0 Hz时,根据式(6),由表 1参数建立多径仿真信道.其中最大多径时延为12 ms,且第二径的信号幅度衰减为源信号的0.82倍,对第一径信号干扰比较大,则该多径信道造成的码间干扰会比较严重.相关仿真参数见表 1、2.
| 表 1 信道的时延和幅度衰减 |
| 表 2 系统仿真参数 |
在多径仿真信道下,由式(5)可得SC-FDE系统、OFDM系统和WFRFT系统的误比特率.3种系统在不同信噪比下的误比特率曲线见图 7.由图 7可见,当信噪比<14 dB时,3种系统的性能排序为OFDM < WFRFT < SC-FDE;当信噪比>14 dB时有SC-FDE < WFRFT < OFDM.图 8给出不同信噪比下WFRFT系统在α主周期内的误比特率曲线.图 7中,信噪比分别为10、18 dB时,SC-FDE系统误比特率为1.5×10-1、7.6×10-4,OFDM系统为5.3×10-2、1.1×10-2.结合图 8可见,WFRFT系统随α的不同呈现周期变化,但误比特率一直在SC-FDE和OFDM间波动.综合图 7、8可得,基于WFRFT的混合载波系统在多径信道下的性能处于OFDM和SC-FDE系统之间.
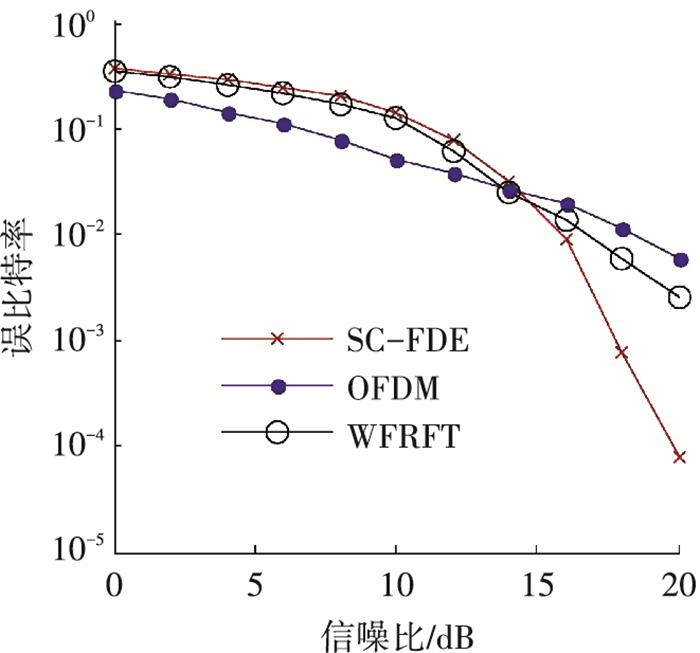
|
图 7 3种系统在不同信噪比下的误比特率(α=0.5) |

|
图 8 不同变换阶次下的混合载波系统性能 |
因为WFRFT系统可兼容单/多载波系统,经过最优阶算法,在低信噪比下系统选取α=1,WFRFT系统转换为OFDM系统,此时系统得到最低误比特率;在高信噪比下系统选取α=0,WFRFT系统转换为SC-FDE系统,此时系统得到最低误比特率.在多径信道下,基于WFRFT的混合载波系统可依具体情况选择最优阶,从而更好地匹配信道,达到最优性能.仿真结果见图 9.
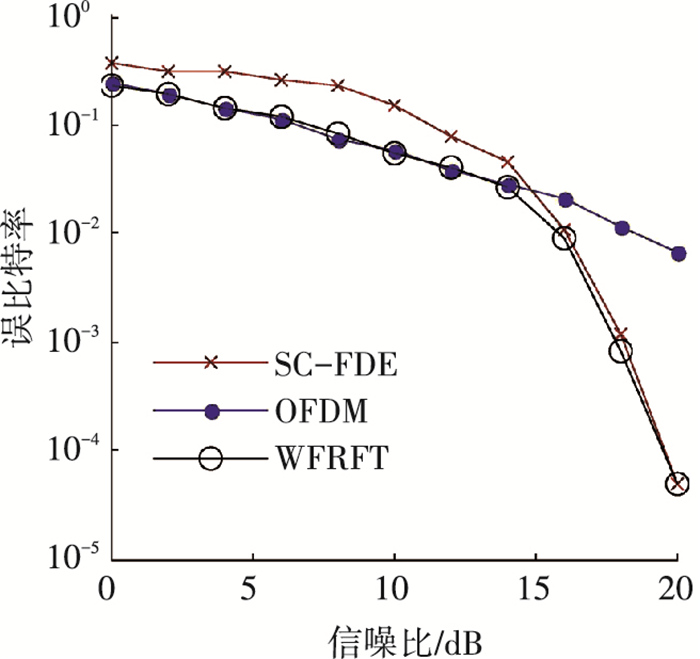
|
图 9 3种系统在不同信噪比下的误比特率(α可变) |
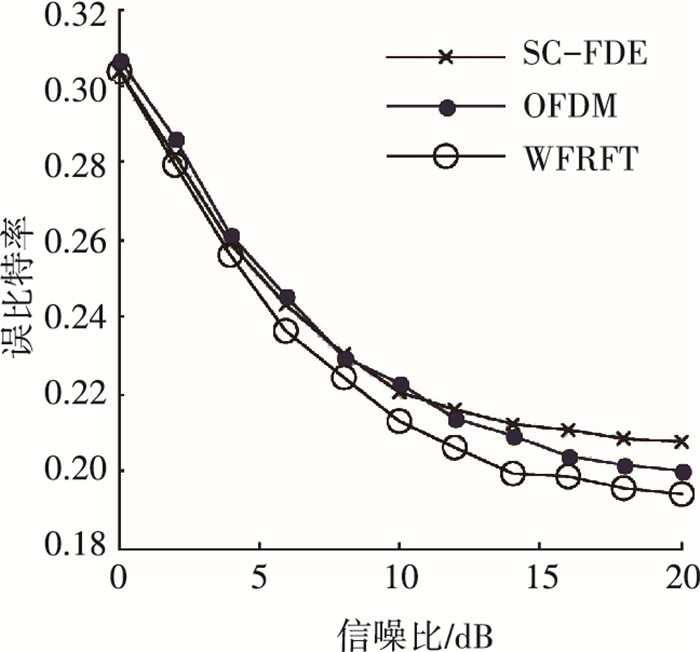
另外,作为单/多载波混合体制存在的WFRFT系统对时间选择性衰落与频率选择性衰落都存在抵抗性,从而比单独的单/多载波系统拥有更优异的系统性能.因此,在多径和多普勒信道下进行仿真,最大多普勒频移为200 Hz,具体仿真参数见表 1、2.在该双选信道下,混合系统经过最优化过程,选取α=0.4,此时系统得到最低误比特率.仿真结果见图 10.
|
图 10 3种系统在双选信道下的性能比较 |
由图 10可见,信噪比在0~5 dB时,3种系统的误比特率相差不大;信噪比>5 dB时,基于WFRFT的混合载波系统的误比特率很明显低于其它两种系统.以信噪比为20 dB为例,WFRFT系统比OFDM系统的误比特率降低0.008,比SC-FDE系统降低0.017,显示出WFRFT系统比其它两种系统具有更强的抗衰落能力,有一定实用价值.
综上所述,基于WFRFT的混合载波系统只需一套物理层传输设备,可根据不同信道环境选择合适的α,以更好地匹配信道,比传统的单/多载波系统具有更好的性能.
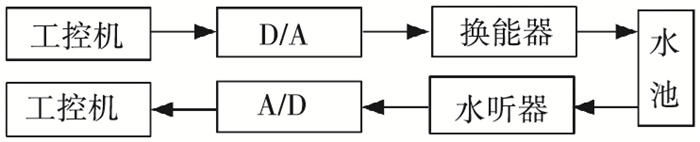
4.2 水池实验该实验是在厦门大学通信工程系实验水池中完成的.水池4面铺设瓷砖,声信号在水池中传输时存在严重的多径时延.实验过程见图 11,换能器和水听器相距8 m.系统参数的设置见表 3.
|
图 11 水池实验过程示意 |
| 表 3 实验系统参数 |
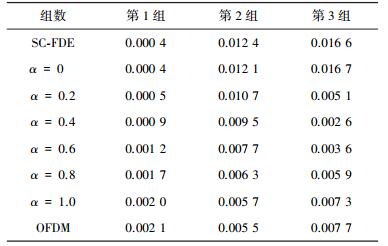
换能器和水听器保持静止,此时信道表现为多径时延特性,在信噪比估计值分别为18.801 0、12.658 8 dB时得到第1、2组数据;水听器以20 m/s的速度移动造成约147 Hz的最大多普勒频移,此时信道表现为多径时延和多普勒频移的特性,在该信道下得到第3组数据.实验数据见表 4.
| 表 4 水池实验结果(误比特率) |
由表 4第1、2组数据可得,WFRFT系统性能介于其它两种系统之间.在信噪比为18.801 0 dB且α=0时,WFRFT系统与SC-FDE系统性能相近,可得最小误比特率;在信噪比为12.658 8 dB且α=1时,WFRFT系统与OFDM系统性能相近,可得最小误比特率.由表 4第3组数据可得,WFRFT系统有优于其它两种系统的变换阶次,当α=0.4时,WFRFT系统的误比特率最低.
因此,在不同信噪比以及多径、多普勒的信道环境下,WFRFT系统通过选取最优阶可得最优系统性能.与传统的单/多载波系统相比,WFRFT系统具有更好的性能.
5 结语现有的两种载波系统—单载波系统和多载波系统,各自存在优缺点.本文提出的WFRFT混合载波系统能体现单/多载波系统混合的特性,通过研究该系统在多径信道和双选信道下的性能,结合信道特点和WFRFT变换性质,以最低误比特率为优化目标,可得系统最优阶,得到在不同传输环境下的最优传输系统.最后经过实验验证:该混合系统在多径信道下,系统性能处于单/多载波系统之间;在双选信道下,混合系统有优于其它两种系统的变换阶次.混合系统可根据信道环境选择最优阶,使系统跟信道匹配,保持最优的系统性能,具有一定应用前景.
| [1] |
WANG Zhaohui, HUANG Jie, ZHOU Shengli, et al. Iterative receiver processing for OFDM modulated physical-layer network coding in underwater acoustic channels[J]. IEEE Transactions on Communications, 2013, 61(2): 541-553. DOI:10.1109/TCOMM.2012.022513.120085 |
| [2] |
郭瑜晖, 孙海信, 程恩, 等. 水声系统单载波频域均衡方法比较[J]. 厦门大学学报(自然科学版), 2012, 51(5): 849-853. |
| [3] |
徐小卡, 桑恩方, 李娜, 等. 基于DFT的OFDM水声通信信道估计算法[J]. 数据采集与处理, 2009, 24(1): 44-48. |
| [4] |
黄新林, 王钢, 马永奎, 等. 一种高效的OFDM比特功率分配算法[J]. 哈尔滨工业大学学报, 2010, 42(9): 1379-1382. DOI:10.11918/j.issn.0367-6234.2010.09.007 |
| [5] |
王荆宁, 沙学军, 谭学治. 单载波频域均衡中的协作分集方法[J]. 哈尔滨工业大学学报, 2011, 43(7): 42-45. DOI:10.11918/j.issn.0367-6234.2011.07.009 |
| [6] |
MEI Lin, SHA Xuejun, ZHANG Naitong. The approach to carrier scheme convergence based on 4-weighted fractional Fourier transform[J]. IEEE Communication Letters, 2010, 14(6): 503-505. DOI:10.1109/LCOMM.2010.06.092413 |
| [7] |
MEI Lin, SHA Xuejun, RAN Qinwen, et al. Research on the application of 4-weighted fractional Fourier transform in communication system[J]. Science China (Information Sciences), 2010, 53(6): 1251-1260. DOI:10.1007/s11432-010-0073-1 |
| [8] |
WANG Kun, SHA Xuejun, MEI Lin. On interference suppression in doubly-dispersive channels with hybrid single-multi carrier modulation and an MMSE iterative equalizer[J]. IEEE Wireless Communications Letters, 2012, 1(5): 504-507. DOI:10.1109/WCL.2012.071612.120359 |
| [9] |
WANG Kun, SHA Xuejun, MEI Lin, et al. Performance analysis of hybrid carrier system with MMSE equalization over doubly-dispersive channels[J]. IEEE Communications Letters, 2012, 16(7): 1048-1051. DOI:10.1109/LCOMM.2012.050112.120414 |
| [10] |
CVIJETIC N. OFDM for next-generation optical access networks[J]. Journal of Lightwave Technology, 2012, 30(4): 384-398. DOI:10.1109/JLT.2011.2166375 |
 2016, Vol. 48
2016, Vol. 48