2. 电力科学研究院 云南电网有限责任公司, 650217 昆明;
3. 南京航空航天大学 航天学院, 210016 南京;
4. 中国航天科技集团 五○二研究所, 100190 北京
2. Electric Power Research Institute, Yunnan Power Grid Company Limited, 650217 Kunming, China;
3. College of Astronautics, Nanjing University of Aeronautics and Astronautics, 210016 Nanjing, China;
4. 502 Research Centre, China Aerospace Science and Technology Corporation, 100190 Beijing, China
认知无线电CR(cognitive radio)基于软件无线,是一种提高频谱资源利用率的智能无线通信技术[1],它允许次用户SU(secondary user)使用政府固定分配给主用户PU(primary user)的授权频谱,但前提是SU不能给PU的正常通信带来干扰[2].因此,SU必须使用频谱感知技术检测信道中是否存在PU,只有当PU空闲时,SU才能进行通信[3].CR最常使用的频谱感知技术是能量感知,能量感知只需将接收信号的能量统计值与预先设定的门限作比较即可确定PU是否存在,所以能量感知简单、易行,并且不需要PU信号的任何先验信息[4].
SU采用“先听后传”策略使用PU信道,即在每个帧的开始SU首先感知PU,如果检测到PU空闲,接下来的时间内SU才传输数据[5].多信道CR允许SU同时利用多个感知到的空闲子信道进行数据传输,因此吞吐量会提高[6].文献[7-8]指出CR的性能取决于感知时间和感知门限,较长的感知时间虽然会提高感知性能,但也会降低SU的数据传输时间;较小的感知门限虽然能提高检测概率,但也会增加虚警概率并降低SU的频谱利用率.因此,选择合适的感知时间和门限对提高CR的性能是非常必要的.文献[9-10]提出通过优化SU在每个子信道上的频谱感知门限,在保证子信道频谱感知性能的基础上,可以提高SU的吞吐量,但是没有考虑如何设置感知时间.文献[11-12]则提出在保证检测概率的前提下,通过优化感知时间可以增加SU的吞吐量,但是却假定感知门限是固定的并由检测概率确定.为此,本文提出联合分配频谱感知时间和门限,进一步提高SU的吞吐量.
1 能量感知由于能量感知不需要信号的先验信息就能够准确检测PU,因此被广泛应用于CR的频谱感知中.假设CR可用的信道数为L,子信道l(l=1, 2, …, L)上SU的接收信号yl为
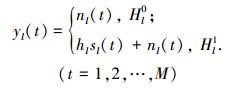
|
式中:t是采样序列,sl是功率为pls的PU信号,nl是功率为σl2的高斯白噪声,hl是子信道l上PU和SU间信道增益,M是采样点数目,Hl0和Hl1分别表示PU空闲和工作两种假设状态.如果感知时间为τ、采样频率为fs,M表示为

|
(1) |
能量感知首先计算接收信号yl的能量统计值Yl,表示为
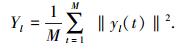
|
yl(1), yl(2), …, yl(M)是独立同分布的变量,因此当M足够大时,Yl近似服从高斯分布,表示为
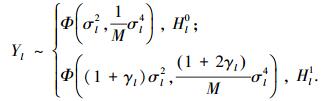
|
(2) |
式中:Φ(a, b)表示均值为a、方差为b的高斯分布,γl=hl2pls/σl2为感知信噪比RSN (signal to noise ratio).
能量感知将Yl与预先选定的门限εl作比较,如果Yl < εl判断PU空闲,反之判断PU存在.当PU空闲而SU错误检测到PU存在时,SU会损失频谱接入机会,表现为虚警概率Plf;当PU存在且SU正确判断PU工作时,SU会躲避PU避免产生干扰,表现为检测概率Pld.根据式(1)和式(2),Plf和Pld是关于τ和εl的函数,分别表示为

|
(3) |
式中函数
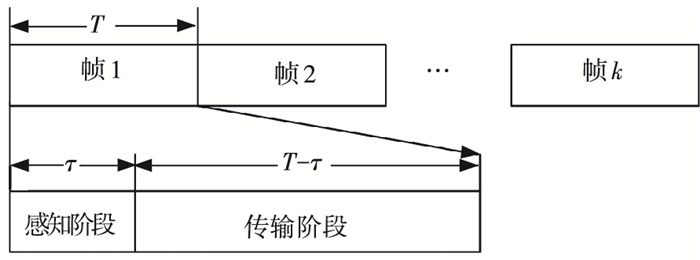
如图 1所示,SU的帧结构被分为感知和传输两个阶段,SU在传输前需要在感知阶段检测PU,只有当检测到PU空闲时,SU才能在传输阶段使用信道通信[13].假设帧长为T、感知时长为τ,则SU的传输时长为T-τ. SU在子信道l上的传输情况分为两种[14]:1) SU正确检测到PU空闲,空闲概率为1-Plf、传输速率为cl0=log2(1+γlSU),其中γlSU为SU接收自身信息的RSN;2)正在工作的PU被SU错误检测为空闲,漏检概率为1-Pld、传输速率为cl1= 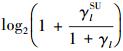
|
图 1 SU帧结构 |
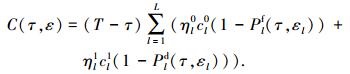
|
(4) |
式中:门限向量ε=[ε1, ε2, …, εL],ηl0和ηl1分别是Hl0和Hl1的出现概率.
PU的传输情况分为3种:1)在感知时间τ内,SU不传输,PU传输速率为rl0=log2(1+γlPU),其中γlPU为PU接收自身信息的RSN;2)传输时间T-τ内,SU准确检测到PU存在且检测概率为Pld,SU不会使用信道,PU传输速率为r0;3) T-τ内,SU漏检PU存在且漏检概率为1-Pld,SU使用信道并对PU产生干扰,PU传输速率为r1= 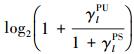
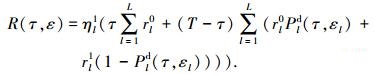
|
(5) |
本文通过优化感知时间τ和门限向量ε,在保证PU吞吐量R、子信道虚警概率Plf和检测概率Pld的基础上,最大化SU的吞吐量C,表示为
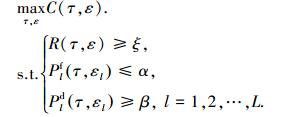
|
(6) |
式中:ξ是PU满足通信需求的最小吞吐量,α和β分别是SU满足感知性能要求的最大虚警概率和最小检测概率且α≤0.5和β≥0.5.式(6)是多变量优化问题,可以采用交替方向优化进行求解[15].求解思想是:给定感知时间τ为一初始值,搜索最优的门限向量ε*最大化吞吐量C,然后给定ε=ε*,搜索最优的感知时间τ*最大化C;给定τ=τ*,重新优化;通过若干次迭代优化,可获得优化问题的最优解.
3.1 感知门限优化初始化τ=τ0,将Plf(τ0, εl)≤α和Pld(τ0, εl)≥β代入式(3)得到εmin≤εl≤εlmax,εlmin和εlmax分别表示为
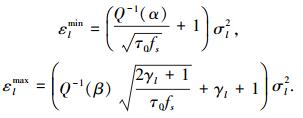
|
将R(τ0, ε)≥ξ代入式(5)得到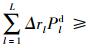

|
因此,式(6)简化为关于ε的优化问题,表示为

|
(7) |
暂不考虑约束εlmin≤εl≤εlmax,利用拉格朗日乘子算法求解式(7),函数式表示为
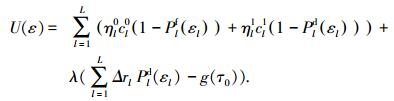
|
式中λ是拉格朗日乘子.εl可以通过∂U(ε)/∂εl=0(l=1, 2, …, L)获得,表示为
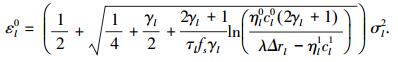
|
(8) |
将式(8)代入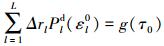
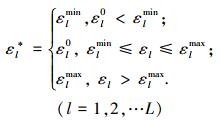
|
(9) |
在3.1节中给定初始感知时间τ=τ0,求得了最优门限向量ε1*=[ε*, ε2*, …, εL*]并获得相应的检测概率Pld(τ0, εl*).下面给定ε=ε*,搜索最优的感知时间τ=τ*最大化C.根据式(3),虚警概率可以由检测概率表示为

|
(10) |
为了保证R(τ, ε)≥ξ和Pld(τ, εl)≥β成立,显然需要Pld(τ, εl)≥Pld(τ0, εl*).由于Q(x)是单调递减函数,根据式(10)可知Plf(τ, εl)≥Plf(τ0, εl*),根据式(4)可知C(τ, ε)≤C(τ0, ε*).因此,只有当Pld(τ, εl)=Pld(τ0, εl*)=φl时,C能够取得最大值.将Pld=φl和式(10)代入式(6),关于τ的优化问题表示为
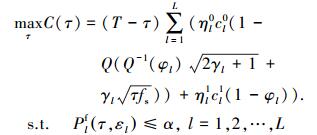
|
(11) |
将式(10)代入Plf(τ, εl)≤α(l=1, 2, …, L)得到
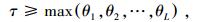
|
式中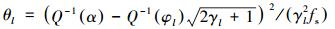
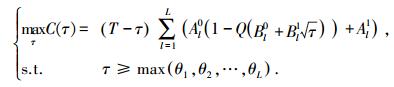
|
(12) |
式中:

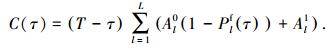
|
求解C(τ)关于τ的二阶导数,表示为
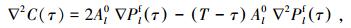
|
(13) |
求解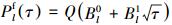
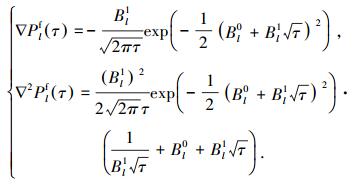
|
(14) |
由Bl1>0以及Plf≤α≤0.5得到

|
(15) |
联合优化算法基于交替方向优化,具体步骤如下:
1) 初始化k=1、τ(k)=0、ε(k)={0}和估计误差ξ;
2) 令τ(k)=τ0(τ0为0~T任意数);
3) 代入τ(k),根据式(9)求解最优向量ε*;
4) 令ε(k+1)=ε*;
5) 代入ε(k+1),根据式(15)求解最优值τ*;
6) 令τ(k+1)=τ*和k=k+1;
7) 重复步骤3)~6)直至|τ(k)-τ(k-1)|≤ξ且‖ε(k)-ε(k-1)‖2≤ξ;
8) 联合最优解为τ=τ(k)和ε=ε(k).
联合优化算法的时间复杂度和估计误差ξ有关,表示为O(1/ξ2).
4 仿真分析仿真中,帧长T=1 s,噪声功率σl2=1 mW,子信道数L=10,最大虚警概率α=0.5,最小检测概率β=0.9,假设概率ηl0=ηl1=0.5,SU和PU的子信道发射功率为10 mW,信道增益服从均值为-10 dB的瑞利分布,估计误差ξ=0.01.
图 2是不同感知RSN下,SU的吞吐量C随平均感知门限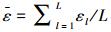
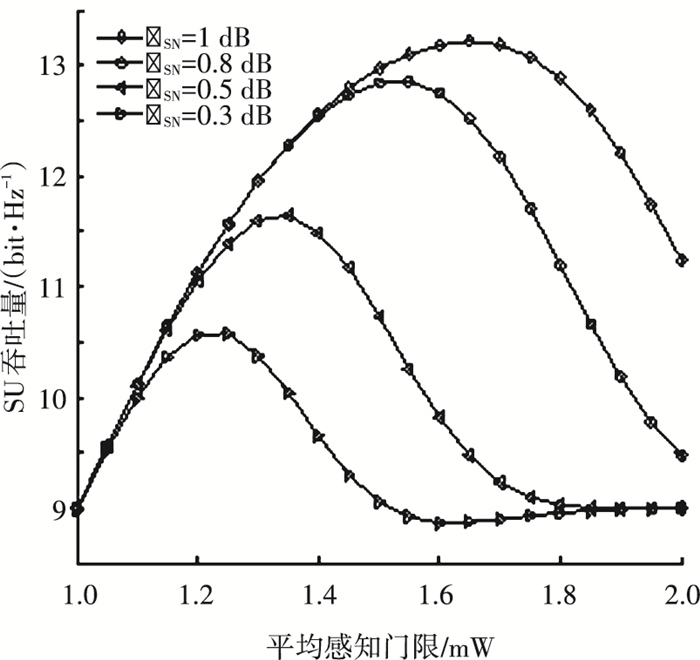
|
图 2 SU吞吐量随感知门限变化 |

|
图 3 SU吞吐量随感知时间变化 |
图 4是不同算法下,SU吞吐量随PU吞吐量的变化.图 4比较了本文感知时间和门限联合分配算法、文献[12]提出的优化感知时间的感知吞吐量折中方案、文献[9]提出的多信道感知门限优化方案以及传统的固定感知时间和门限方案.可以看出,在PU吞吐量给定的情况下,联合分配算法能够使SU获得更高的吞吐量,而感知吞吐量折中方案和多信道感知门限优化方案由于仅优化感知时间或感知门限,其性能要低于联合分配算法,但是要好于固定感知时间和门限方案.
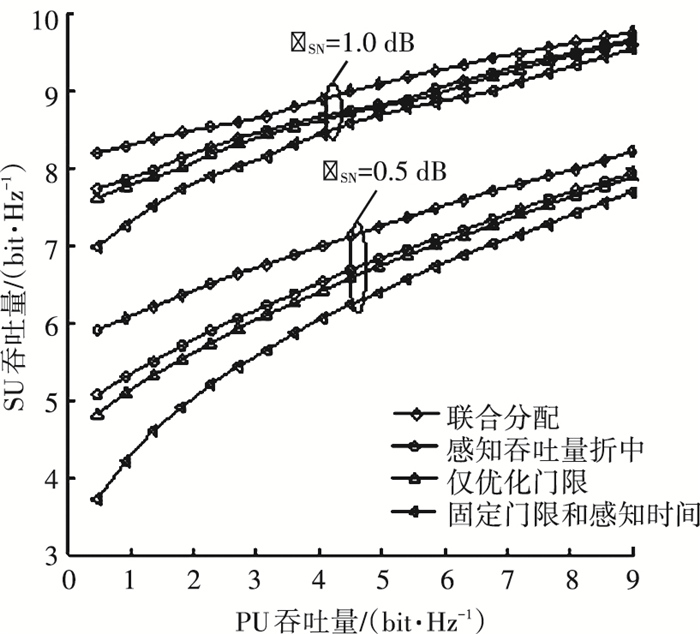
|
图 4 SU吞吐量随PU吞吐量变化 |
本文基于“先听后传”的次用户帧结构,建立了频谱感知时间和子信道感知门限的联合优化分配模型,以最大化多信道CR中SU的吞吐量.采用交替方向优化将联合优化分解为分别关于感知时间和感知门限的两个单变量子优化问题,理论和仿真表明两个子优化问题是凸优化且存在最优解,交替优化两个子优化问题可以获得最终解.在PU吞吐量给定的情况下,联合分配能够使SU获得更高的吞吐量.下一步会考虑将联合分配应用到多用户场景中.
| [1] |
MITOLA J, MAGUIRE G Q. Cognitive radio:making software radios more personal[J]. IEEE Person Communication, 1999, 6(4): 13-18. DOI:10.1109/98.788210 |
| [2] |
HAYKIN S. Cognitive radio:brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220. DOI:10.1109/JSAC.2004.839380 |
| [3] |
GHASEMI A, SOUSA E S. Spectrum sensing in cognitive radio networks:requirements, challenges and design trade-offs[J]. IEEE Communications Magazine, 2008, 46(4): 32-39. DOI:10.1109/MCOM.2008.4481338 |
| [4] |
刘鑫, 谭学治, 徐桂森. 噪声不确定下认知无线电能量检测性能的分析[J]. 四川大学学报(工程科学版), 2011, 43(6): 168-172. |
| [5] |
MARINHO J, MONTEIRO E. Cooperative sensing-before-transmit in ad-hoc multi-hop cognitive radio scenarios[C]//International Conference on Wired Wireless Internet Communications. Santorini: Springer Press, 2012: 186-197.
|
| [6] |
FAN Rongfei, JIANG Hai. Optimal multi-channel cooperative sensing in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2010, 9(3): 1128-1138. DOI:10.1109/TWC.2010.03.090467 |
| [7] |
丁汉清, 杨家玮, 赵志远. 认知无线电系统中感知时间的优化[J]. 华中科技大学学报(自然科学版), 2011, 39(8): 84-87. |
| [8] |
LIU Xin, JIA Min, TAN Xuezhi. Threshold optimization of cooperative spectrum sensing in cognitive radio network[J]. Radio Science, 2013, 48(1): 23-32. DOI:10.1029/2012RS005009 |
| [9] |
ZHI Quan, SAYED A H, POOR H V. Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1128-1140. DOI:10.1109/TSP.2008.2008540 |
| [10] |
MICHELE S, MAURIZIO M. Optimization of non-convex multiband cooperative sensing with genetic algorithms[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1): 87-96. DOI:10.1109/JSTSP.2010.2054064 |
| [11] |
LIANG Y C, ZENG Y H, EDWARD C Y, et al. Sensing-throughput tradeoff for cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(4): 1326-1336. DOI:10.1109/TWC.2008.060869 |
| [12] |
LIU Xin. A new sensing-throughput tradeoff scheme in cooperative multiband cognitive radio network[J]. International Journal of Network Management, 2014, 24(3): 200-217. DOI:10.1002/nem.v24.3 |
| [13] |
EDWARD C Y P, LIANG Y C, GUAN Y L. Optimization of cooperative sensing in cognitive radio networks:a sensing-throughput tradeoff view[J]. IEEE Transactions on Vehicular Technology, 2009, 58(9): 5294-5299. DOI:10.1109/TVT.2009.2028030 |
| [14] |
LIU Xin, JIA Min, GU Xuemai. Joint optimal sensing threshold and subcarrier power allocation in wideband cognitive radio for minimising interference to primary user[J]. China Communications, 2013, 10(11): 70-80. DOI:10.1109/CC.2013.6674212 |
| [15] |
STEPHEN B, NEAL P, ERIC C, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 15-40. |
 2016, Vol. 48
2016, Vol. 48


