量子计算的主体思想就是用微观粒子(量子)的纠缠、叠加和相干等特性解决经典计算中无法解决的NP问题.分解大数质因子的量子算法[1]和量子搜索算法[2]等的提出,给量子计算的研究注入了新的活力,引发了量子计算研究的热潮.量子突出的并行计算能力被应用到各类优化算法中,其中量子遗传算法[2-3]QGA(quantum genetic algorithm)以种群规模小、搜索能力强、收敛速度快等优点受到关注,而双链量子遗传算法DCQGA(double chains quantum genetic algorithm)弥补了量子遗传算法的缺陷,提高了量子优化算法的效率和精度,得到了广泛的应用.
但DCQGA优化算法自身也存在不足.首先,它的编码空间范围为(0, 2π),空间范围较大,影响收敛速度;其次,量子更新策略的步长调整是基于上一次的迭代初值,会导致步长的调整超出合理范围,影响收敛精度;最后,其染色体变异环节采用非门处理,没有达到更新量子比特概率幅的目的.文献[4-5]是比较典型的改进策略,也是目前优化效果最好的改进方案,但都有自身不足.文献[4]对编码空间进行改进但未考虑压缩后编码空间变为单值函数的问题,没有起到增加搜索密度的目的;文献[5]提出利用Hadamard门作为变异操作,但这种操作变异尺度过大,易引起种群退化现象.针对上述缺陷,本文对DCQGA的编码、染色体旋转门更新和变异过程进行改进,提出了一种具有高密度搜索空间、自适应更新步长的F型双链量子遗传算法(F Double Chains Quantum Genetic Algorithm, F_DCQGA),并将该算法引入小波阈值去噪[6]的阈值选择机制中,提出了量子小波阈值去噪法,并通过仿真验证了F_DCQGA算法的实际应用价值.
1 一种改进的双链量子遗传算法 1.1 传统双链量子遗传算法双链量子遗传算法在QGA的基础上做了大量改进[7]:编码方式是采用量子比特的概率幅直接来描述目标函数解空间的可行解,这种编码方式既保证了染色体初始化时的随机性又能同时利用染色体中上下两条基因链在解空间搜索,使种群具有丰富多样性的同时加快了搜索速度;用量子旋转门更新量子比特的相位时,不必繁琐地去比对查找表[8],而是对于转角方向给出了一种简单实用的确定方法;在确定转角迭代步长时充分利用了目标函数的梯度信息;利用量子非门完成对量子比特的变异操作,使种群不断的进化.虽然DCQGA有很多优势但自身也存在不足:它的编码空间过大、量子更新步长不合理等问题导致其搜索速度慢、搜索精度低、鲁棒性差等缺陷[9].本文针对DCQGA中的量子比特的编码空间、旋转门和变异门的染色体更新策略进行改进.
1.2 改进的量子比特编码区别传统编码方式,在双链量子遗传算法中染色体的量子基因位采用量子比特编码.在量子计算中,用|0〉和|1〉来表示量子的两种基本状态,量子比特状态除了|0〉和|1〉还可以处于二者之间的某一线性组合,通常称为叠加态[10-12].一个量子比特的状态可以描述为
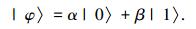
|
其中α和β是一对复数,称为量子态的概率幅且α2+β2=1[13].在DCQGA中量子位的概率幅用cos(t)sin(t)T来表示,直接采用量子比特的概率幅进行编码,其中t=2π×rand,rand为(0, 1)内的随机数.概率幅在单位圆中幅角t的初始值由(0, 2π)随机产生.则在采用双链编码方案时可以表示为
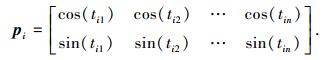
|
其中tij=2π×rand,i=1, 2, …, m,j=1, 2, …, n,m是种群规模,n是量子位数.
量子比特的概率幅(cos(tij), sin(tij))T是周期变化的,每条量子染色体量子比特的概率幅在更新过程中都会重复落在单位圆中,取值范围在(-1, 1)内,这样的搜索范围大,会影响算法的收敛速度.
本文对双链量子遗传算法的编码空间进行了改进,将量子比特编码的初始相位角t′ij限定在[π/2, 3π/2]内,则t′ij=π/2+π×rand,概率幅取值范围仍在(-1, 1)内,既保证了量子种群适应度值与相应幅角排序的单调性还压缩了编码空间,提高了概率幅的密度.但缩小编码空间会减小最优解的搜索概率,如图 1所示.当编码空间范围为(0, 2π)且对应概率幅值为-0.4时,有两个相位解P1和P2;当编码空间为(π/2, 3π/2)时,对应的相位解仅有P1这一个解,这样会减小搜索到全局最优解的概率,降低搜索精度.为此在双链编码时引入一个调整因子k来弥补这个缺陷.改进的双链编码方式为

|
图 1 编码空间示意 |
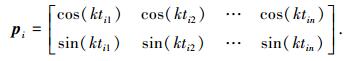
|
(1) |
其中引入的调整因子k为大于等于1的常数.
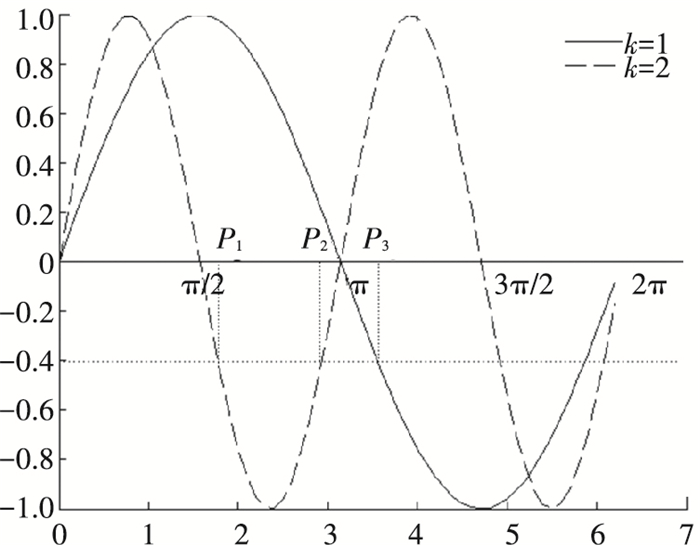
当k =1时为传统的双链编码方式;当k > 1时压缩了概率幅函数的周期,提高搜索全局最优解的概率.如图 2所示,当k = 1且编码空间范围为(π/2, 3π/2)时,概率幅为-0.4,对应的相位角仅有P3;当k = 2且编码空间也为(π/2, 3π/2)时,概率幅为-0.4,对应的相位角有P1和P2两个解.理论上,当k取值更大时,对应概率幅的相位角更多,搜索概率更高.但k取值过大又会导致编码空间对应的相位角密度过大,反而影响了收敛精度,综合考虑调整因子k选为3.
|
图 2 k = 1和k = 2时编码空间示意 |
在量子计算中,利用量子门[14]对量子位进行一系列的酉变换来实现某些逻辑变换功能.常见的量子门有Hadamard门、相位门、量子旋转门等,本文用量子旋转门来更新量子比特相位作为进化操作的执行机构,它决定了量子遗传算法的性能.量子旋转门定义为

|
其中θ是旋转角度,在DCQGA第i个量子比特的更新过程可以表示为
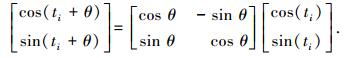
|
其中(cos(ti), sin(ti))T和(cos(ti+θ), sin(ti+θ))T为第i个量子比特更新前后的概率幅.
旋转角度θ的大小和旋转方向会影响到算法的速度和效率,对θ方向的选取做如下规定:
α0和β0是搜索到的全局最优解中的某一个量子比特的概率幅,α1和β1是当前解中的相应量子比特的概率幅,令
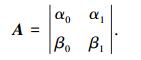
|
当A≠0时,θ的方向为-sgn(A);当A=0时,θ的方向取正负均可[15].
转角的大小决定了算法的收敛速度和搜索精度,由文献[10-11]可知,量子旋转门转角Δθ的取值范围是Δθ0≥|Δθ|≥0.1Δθ0.当Δθ0≤0.001π时,Δθ0的变化率很小,降低了算法的收敛速度和效率;当Δθ0≥0.01π时,容易引起早熟收敛.文献[10]给出了Δθ的取值范围为(0.005π, 0.01π),但没有给出具体的选择依据,这种转角大小固定的更新策略没有考虑种群中染色体之间的差异,也没有充分利用搜索点处目标函数的相对变化率.
因此,在FDCQGA中考虑到转角Δθ和迭代初始值Δθ0应随着目标函数在搜索点处相对变化率的变化而做出相应的调整,当适应度函数在搜索点处的变化率较大时,适当减小搜索步长,反之适当加大搜索步长,这样就可以防止搜索速度过慢和算法振荡的问题.提出了一种自适应步长系数,将目标函数的在搜索点处的相对变化率加入到转角步长函数中.令自适应步长系数为
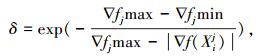
|
∇f(Xij)为目标函数f(X)在点Xij处的梯度,∇fjmax和∇fjmin分别定义为
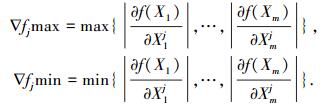
|
其中Xij(i=1, 2, …, m; j=1, 2, …, n)表示向量Xi的第j个分量,m表示种群规模,n表示单个染色体上的量子位数.综合上面提到的转角方向策略、自适应步长策略和文献[16]给出的Δθ取值范围,在F_DCQGA中量子旋转门的转角函数Δθ定义为
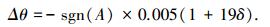
|
通过这样定义转角函数可以看出,在搜索点处当目标函数变化率较小时,Δθ在增大,从而加快收敛速度;当目标函数变化率较大时,Δθ在减小,从而减缓收敛速度,防止跃过全局最优点,保证Δθ在一个合理的范围内变化,提高搜索精度.
1.4 改进的量子染色体变异在传统遗传算法中,为降低算法早熟的概率同时又能增加种群多样性,加入了变异操作. DCQGA利用量子非门实现变异过程,这种变异操作实际上是互换了染色体中基因位的两个概率幅,并没有增加种群的多样性.为了既能保证增加种群的多样性又不会因为相位角调整过大而跃过全局最优解,提出了π/6变异门,定义如下:
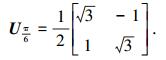
|
π/6变异门作用在单个量子比特的效果为

|
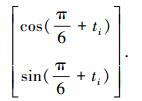
|
(2) |
可以看出,这种变异策略也是一种相位角旋转,但这种旋转改变了基因位的幅值,增加了种群多样性;同时相位角的旋转角度为30°,既不会因为旋转角度过小起不到变异作用也不会因为相位角调整过大而跃过全局最优解.
2 基于F_DCQGA的小波阈值去噪法 2.1 小波阈值去噪概述小波阈值去噪算法可以通过三步来实现:
1) 确定小波基函数和小波分解尺度,对含噪信号做小波变换获得小波系数;
2) 选择合适的阈值函数和阈值估计法,对小波系数进行处理;
3) 将处理后的小波系数进行小波重构,获得去噪后的信号.
小波阈值去噪的关键是阈值和阈值函数的选取.目前常用的阈值是Donoho提出的固定阈值法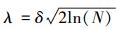
常用的阈值函数有硬阈值函数和软阈值函数:硬阈值函数在阈值点的不连续会导致重构信号产生振荡现象;虽然软阈值函数是连续函数可以克服上面的缺陷,但滤波后的小波系数与原系数之间总是存在固定偏差,造成边缘模糊影像重构图像.因此,很多研究者都对阈值函数提出改进且效果优异,本文选取的阈值函数为
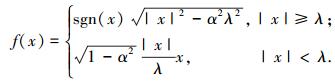
|
(3) |
式中:f(x)为滤波后的小波系数;x为小波分解系数;λ为阈值;α为调整参数,只要参数α的取值适当便可以获得较好的去噪效果,本文中的参数α取值为0.8.
2.2 基于F_DCQGA的阈值选取目前对于小波阈值的改进大部分还是在如何确定一个最优的固定阈值,即在小波分解的不同层数选用相同的阈值.而信号和噪声在小波变换域内随着尺度的变化所呈现出的变化规律是不同的,噪声的小波分解系数会随着尺度的增加而减小,而信号的变化规律正好相反.因此,这种固定阈值的方式是不科学的.在确定阈值时需要考虑到各层中信号和噪声层间系数的相关特性,由文献[17]可知,噪声对应的第j+1层小波展开系数的最大值小于第j层小波展开系数的最大值的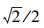
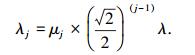
|
(4) |
根据小波变换的系数特征在原阈值的基础上引入自适应因子μj,μj∈[0, 1],j为当前分解尺度的层数,λ为Donoho提出的阈值.在自适应阈值中自适应因子起到了举足轻重的作用,它的值会随着信号和噪声强度、小波分解尺度的变化而变化,这就需要一个快速、稳定的寻优体制来寻找最优的μj值.因此,将F型双链量子遗传算法引入到小波去噪中提出量子小波去噪,将F_DCQGA作为这个寻优体制来寻找最佳的μj值,利用F_DCQGA的快速、稳定来获得每一层的最佳阈值.
2.3 量子小波去噪法中的适应度函数为了保证搜索到最优阈值调整因子是合理的,需要一个与图像质量有关的适应度函数来决定量子染色体中基因的进化方向和步长.常用的图像去噪效果评估手段有主观和客观评价准则,主观评价通过人眼观察得出结论;客观评价准则通过对比均方误差(SME)和峰值信噪比(RPSN)的值来评价.去噪后的图像均方误差值越小和峰值信噪比越大,去噪效果越好.由于SME与RPSN值存在一一对应关系,所以将峰值信噪比作为适应度函数来指导量子染色体的进化方向,适应度函数为

|
(5) |
其中f(m, n)和f′(m, n)分别为图像的灰度值,且RPSN=-10lg(2552/SME).
2.4 基于F型双链量子遗传算法的小波阈值去噪方法F_DCQGA算法对信号进行小波阈值去噪的具体步骤:
1) 读入信号数据s(x),加入噪声获得含噪信号f(x),并利用式(5)计算出加噪信号的峰值信噪比(RPSN, 0).
2) 选择小波基函数、确定小波分解层数j=3,对加入噪声的信号f(x)进行多尺度小波分解,获得小波系数W(f(x)).
3) 算法参数设置:种群规模m,染色体基因位数n,最大迭代次数gen,变异概率Pm.
确定种群规模及基因位数.种群规模与小波分解层数一致,所以种群规模为m=j.染色体中基因位数过大会增加运算的复杂程度,影响算法效率,而基因位数过少又会降低搜索精度.综合考虑既保证计算量不能太大又能满足搜索精度的基因位数定为n=20,这样的基因位数便保证算法在全局范围内搜索又能降低计算复杂度.最大迭代次数根据仿真实验给出,F_DCQGA算法在复杂函数进行寻优时一般会在50代内收敛到最优解(后面仿真实验可看到),F_DCQGA算法以最大迭代次数作为算法终止条件,为了保证搜索精度文中的最大迭代次数为gen=100,变异概率Pm=0.05.
4) 令t=0,种群初始化.采用本文提出的高密度编码方式,在[0, 1]范围内随机生成一个数rand,利用公式t=(π/2+π×rand)在[π/2, 3π/2]范围产生20个随机数tn.按式(1)产生m条20个基因位的染色体做为初始种群Q(t0m), 调整因子k取值为3.
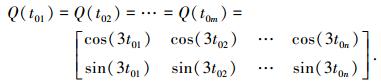
|
5) 解空间变换.按如下公式将初始化种群中的上下两条并行基因链所表示的近似解与搜索空间内的优化解建立一一映射关系(本文中优化解空间范围为U=[0, 1]):
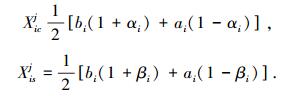
|
式中:[αi, βi]为第i个基因位;Ω=[ai, bi)为解空间范围.
6) 计算染色体中各个基因位的适应度值f(xi),记录最优解f(xbest)及最优基因位.将初始种群中的2mn个解作为自适应因子μj的初始值.将初始值带入阈值选择机制式(4)中作为不同尺度下的阈值,利用得到的阈值和阈值函数对步骤2)中获得的小波系数W(f(x))进行去噪处理,将去噪后的信号按式(5)计算出m个适应度值,记录m个适应度值中的最优解f(xbest)及最优基因位.
7) 判断是否满足迭代次数gen.若满足条件则终止循环并输出步骤6)中的最优解f(xbest)及最优基因位,利用处理后的小波系数重构信号;否则进行下一步.
8) 利用量子旋转门对种群进行更新.利用量子旋转门对染色体中的每一位基因位完成变换,按照式(3)新的转角函数确定转角大小和方向,生成新的染色体.
9) 利用π/6变异门完成染色体的变异操作.按照式(2)根据概率Pm选择步骤8)中产生的新染色体中的若干量子比特对其实施变异操作, 再次获得新一代的染色体. t = t +1,返回步骤5)继续进化直至满足循环终止条件.
量子小波阈值去噪法的流程图如图 3所示.

|
图 3 基于F_DCQGA的量子小波阈值去噪法流程 |
利用Matlab 2011b仿真软件通过对复杂二元函数求极值的问题将传统遗传算法(GA)、普通的量子遗传算法(QGA)、双链量子遗传算法(DCQGA)和本文提出的F型双链量子遗传算法(F_DCQGA)进行比较,验证F_DCQGA算法的优越性.
选取的复杂二元为Shaffer’s F6函数:
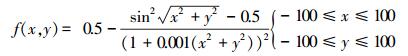
|
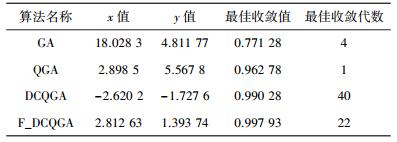
该非线性函数在给定的自变量范围(-100, 100)内有多个局部极值点,只有在(0, 0)点处才为全局最大值,最大值为1,在算法仿真时若最优解大于0.99时便可认为算法收敛.普通的寻优算法容易陷入局部极值点引起算法的早熟现象,比较适合验证寻优算法的性能. F_DCQGA与其他算法的参数设置如表 1所示. 4种算法对Shaffer’s F6函数的优化结果如表 2和图 4所示.从仿真结果看,F_DCQGA算法在4种算法中的优化效率最高,寻优结果也最好.由表 2可以看到,只有F_DCQGA和DCQGA算法总体表现良好,都达到了收敛标准,其中F_DCQGA算法寻优效果最好,其最佳收敛结果为0.997 93、最佳收敛代数为22代,可见F_DCQGA算法无论在收敛速度还是收敛精度上都要优于其他3种算法.
| 表 1 参数设置 |
| 表 2 仿真结果 |
|
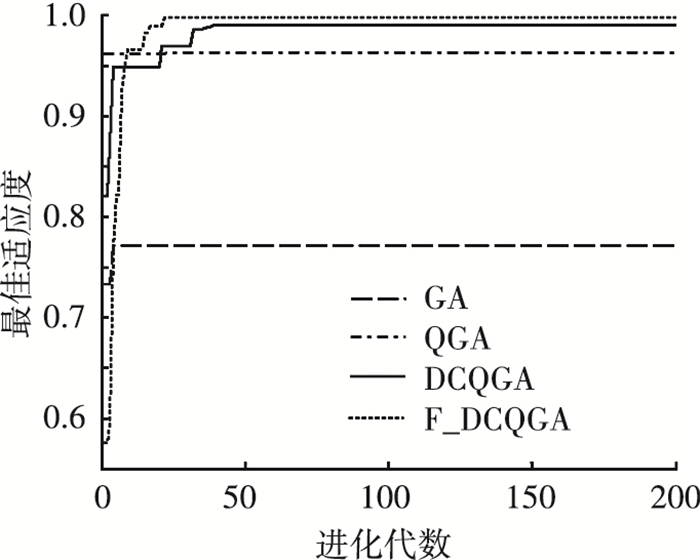
图 4 4种算法进化对比 |
从图 4可以看到,GA和QGA算法陷入局部极值中,没有搜索到全局最优解,算法的寻优能力失效.其中QGA算法最早陷入了局部极值中,这一点是可以预见的.首先,QGA染色体的更新效果差;其次,变异更新没有起到作用.对于这种复杂函数来说,GA、QGA的优化能力基本上已经丧失,而F_DCQGA对于这种复杂函数仍然可以保持良好的优化效率.
F_DCQGA算法的收敛代数少,说明编码方式可以增加搜索空间的密度,提高搜索速度;算法搜索到全局最优解而没有陷入局部极值,说明本文提出的转角步长函数和π/6变异门对染色体的更新更合理、更有效,使量子染色体具有更丰富的种群多样性,避免早熟现象,提高搜索精度.
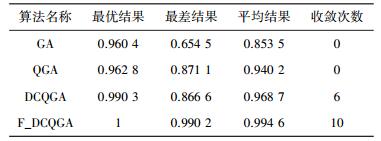
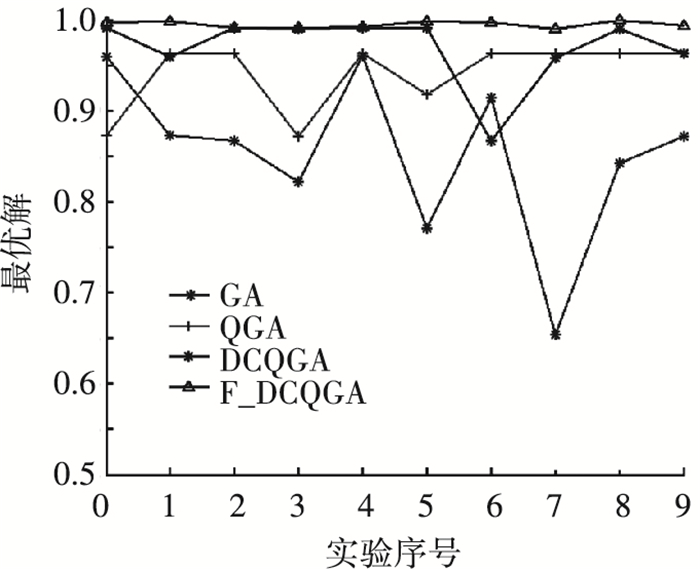
为了更好地验证F_DCQGA算法的稳定性,对Shaffer’s F6函数分别用4种算法进行10次优化仿真,优化结果对比如表 3和图 5所示.从10次仿真结果看到,F_DCQGA算法优化效率仍然最高,虽然DCQGA算法也可以实现寻优目的,但其稳定性较差,曲线波动较大.而F_DCQGA的10次寻优结果基本上一致,说明F_DCQGA算法的鲁棒性要优于双链量子遗传算法.
| 表 3 函数极值优化结果对比 |
|
图 5 Shaffer 's F6优化结果 |
将传统小波阈值去噪、基于QGA的小波阈值去噪和基于F_DCQGA的小波阈值去噪算法进行仿真对比.
对256*256大小的标准灰度图像(见图 6)用Matlab中imnoise函数加入0均值、0.01方差的高斯噪声,加噪后图像的SME为0.096 7、RPSN为14.713 1 db.采用db5小波对含有噪声的图像进行3层小波分解,再分别用上述3种方法去噪,去噪效果如图 7所示.

|
图 6 原始图像 |

|
图 7 噪声图像及3种放发的去噪图像 |
从去噪图像中看到,本文提出的去噪方法在有效去除了噪声的同时还保留图像更多的高频信息,视觉效果有了明显的提高,其他2种算法去噪后的图像仍有部分噪声被保留下来,图像清晰度较差.
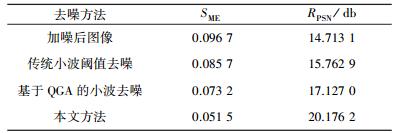
表 4给出了3种算法去噪后图像的均方误差MSE和峰值信噪比RPSN.从表 4可以看出,经过本文方法去噪后图像在这两项指标上得到了较大的改善,均方误差值比另外2种方法均有较大程度的降低,峰值信噪比也有所提高,证明了本文提出的量子小波阈值去噪法对图像的去噪效果更有效.
| 表 4 cameraman图像去噪后的SME和RPSN |
为了验证F_BDCQGA算法比一般算法更具优越性,对选择名为“barbara”的图像进行去噪仿真.由图 8(a)可知,该图像的目标与背景差异较小,灰度值分布均匀,边缘提取较困难,对阈值和阈值函数精度要求较高,适合用来验证去噪方法的有效性.

|
图 8 barbara原始图像及3种方法的去噪图像 |
在“Barbara”图像中同样加入均值为0、方差为0.01的高斯噪声,加噪后图像的均方误差为0.198 3、峰值信噪比为14.188 1 db.小波阈值去噪参数和去噪方法与前面一致,去噪结果如图 8(c)、(d)、(e)所示.
由图 8可知,本文提出的量子小波阈值去噪法效果同样最好,其他2种算法去噪效果相差无异,说明普通量子遗传算法没有起到明显的作用,普通QGA算法与小波阈值去噪法的结合并不是对所有的图像去噪都能达到好的效果.从去噪图像上来看本文提出去噪方法即使针对这种灰度分不均匀的图像也能获得高质量的去噪效果,利用F_DCQGA的小波阈值去噪法对复杂图像去噪也可以保留更多的高频信息,视觉效果有了明显的提高.
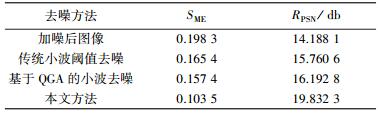
表 5给出了3种算法去噪后图像的均方误差MSE和峰值信噪比RPSN.从表 5可以看出,经过本文方法去噪后图像的均方误差值和峰值信噪比比另外2种方法有较大的改善,量子小波阈值去噪法比其他2种算法在RPSN上提高了近4 db,证明了本文方法对该图像的去噪效果更有效.
| 表 5 barbara图像去噪后的SME和RPSN |
为验证F_DCQGA算法在寻优问题上的优越性具有普遍意义,利用量子小波阈值去噪法对不同信噪比下的“Barbara”图像进行去噪仿真实验,通过实验数据说明算法的有效性、可靠性和普遍性.对“Barbara”图像加入均值为0,方差δ分别为0.005、0.05、0.1、0.5的高斯白噪声,用db5小波基进行3尺度的小波分解.分别用4种小波去噪法去噪,用客观评价准则对去噪效果进行评估,结果如表 6所示.
| 表 6 不同信噪比下3种方法对图像去噪的结果 |
从仿真结果可以看出,在δ=0.005和δ=0.05时,信噪比相对较高,3种算法的去噪效果相差无异;随着信噪比的降低另外2种算法的去噪效果急剧下降,当δ=0.5时传统小波阈值去噪法和QGA的小波去噪法基本上丧失了去噪功能,而本文提出的量子小波去噪法即使在最坏的情况下仍然具有去噪能力. F_DCQGA算法增强了小波阈值去噪法去噪能力,这是源于F_DCQGA算法良好的寻优性能才使得小波阈值去噪法在去噪质量上获得提升.
4 结论F_DCQGA快速、准确的寻优特性与小波阈值去噪方法结合,利用F_DCQGA寻优方面的优越性可提高传统小波阈值去噪法的去噪效果.通过对F_DCQGA的性能仿真说明算法具有寻优速度快、寻优精度高、鲁棒性好等优点.通过对量子小波阈值去噪法的仿真说明,F_DCQGA算法可以引用在其他领域,并对传统算法的性能有提升的作用.
| [1] |
SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring[C]//Proc of the 35th Annual Symp on Foundations of Computer Science. New York: IEEE Comper Society Press, 1994: 124-134.
|
| [2] |
李士勇, 李盼池. 量子计算与量子优化算法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009: 69-78.
|
| [3] |
ZHANG G X, LI N, JIN W D. A novel quantum genetic algorithm and its application[J]. ACTA Electronica Sinica, 2004, 32(3): 476-479. |
| [4] |
沙林秀, 贺星耀, 陈延伟. 一种变步长双链量子遗传算法[J]. 计算机工程与应用, 2012, 48(20): 59-63. DOI:10.3778/j.issn.1002-8331.2012.20.012 |
| [5] |
OM H, BISWAS M. An improved image denoising method based on wavelet thresholding[J]. Journal of Signal and Information Processing, 2012, 3(1): 109-116. |
| [6] |
HANSEN M, YU Bin. Wavelet thresholding via MDL for natural image[J]. IEEE Transaction Information Theory, 2000, 46(5): 1778-1788. DOI:10.1109/18.857790 |
| [7] |
王凌. 量子进化算法研究进展[J]. 控制与决策, 2008, 23(12): 1321-1326. DOI:10.3321/j.issn:1001-0920.2008.12.001 |
| [8] |
HAN K H, KIM J H. Genetic quantum algorithm and its application to combinatorial optimization problems[C]//Proc of IEEE Conference on Evolutionary Computation. Piscataway: IEEE Press, 2000: 1354-1360.
|
| [9] |
周日贵. 量子信息处理技术及算法设计[M]. 北京: 科学出版社, 2013: 19-23.
|
| [10] |
WANG Y, FENG X Y, HUANG Y X, et al. A novel quantum swarm evolutionary algorithm and its applications[J]. Neuro Computing, 2007, 70(4/5/6): 633-640. |
| [11] |
李士勇, 李盼池. 基于实数编码和目标函数梯度的量子遗传算法[J]. 哈尔滨工业大学学报, 2006, 38(8): 1216-1219. |
| [12] |
刘卫宁, 靳洪兵, 刘波. 基于改进量子遗传算法的云计算资源调度[J]. 计算机应用, 2013, 33(8): 2151-2153. |
| [13] |
戴勇谦, 张明武, 祝胜林, 等. 一种新的量子遗传算法变异机制[J]. 计算机仿真, 2013, 30(2): 316-320. |
| [14] |
JIANG Shujuan, ZHOU Qi, ZHANG Yanmei. Analysis on parameters in an improved quantum genetic algorithm[J]. International Journal of Digital Content Technology and Its Applications, 2012, 6(18): 176-184. |
| [15] |
SOUALMIA S, BOULDJEDRI A, BENHAYA A. Semiconductor parameter extraction using cathodoluminescence and genetic algorithms[J]. Materials Science in Semiconductor Processing, 2011, 14(1): 62-68. DOI:10.1016/j.mssp.2011.01.010 |
| [16] |
许少华. 一种改进的双链量子遗传算法及其应用[J]. 计算机应用研究, 2010, 27(6): 2090-2092. |
| [17] |
张兆宁, 董肖红, 潘云峰. 基于小波变换模极大值去噪方法的改进[J]. 电力系统及其自动化学报, 2005, 17(2): 9-12. |
 2016, Vol. 48
2016, Vol. 48