2. 南京信息工程大学 计算机与软件学院, 210044 南京
2. School of Computer and Software, Nanjing University of Information Science and Technology, 210044 Nanjing, China
二进前馈神经网络(BFNN)是一种离散的前馈多层网络,网络中神经元的激活函数通常是硬极限函数或对称硬极限函数.理论上,离散问题可作为连续问题的特例来处理,但是对于那些本质上是离散且连续技术不直接适用的应用领域,如逻辑运算、信号处理、分类与聚类、模式识别等,BFNN比连续神经网络有明显的优势[1].但是由于激活函数的离散性质使得BFNN无法使用成熟的BP算法来对网络进行训练[2-3],迄今为止尚没有高效的学习算法.文献[4-5]针对BFNN提出了MRII算法,但MRII算法会使网络学习陷入局部震荡,成功率不高,并且在训练集样本个数较多的情况下,MRII算法的收敛速度也不理想.文献[6]针对BFNN从几何角度提出了一些几何构造算法,这类算法具有自动确定网络结构的长处,但是随意性大,不能有效控制结构规模.文献[1]在MRII算法的基础上,利用BFNN网络的敏感性技术,对BFNN网络的训练算法进行了进一步的研究和改进,但也存在着网络训练的时间复杂度过高等问题.文献[7-8]针对单隐层连续前馈神经网络提出了极限学习机ELM及其快速学习算法. ELM学习算法通过增加隐层神经元并随机选取权值和偏置, 以及采用最小二乘法求得输出层神经元权值,来使网络达到训练精度要求.只要隐层神经元数目足够多,单隐层的前馈神经网络可以逼近任意的连续函数[9],因此ELM将网络结构限制为单隐层,既不失一般性,又省去了对网络隐层数目的考虑.因为ELM隐层神经元权参数随机给定,需要调节的只是隐层神经元个数和输出层神经元权参数,所以ELM学习算法效率较BP算法要高.但是,也正因为ELM学习算法在增加隐层神经元个数的同时,仅随机给定权参数值,并没有进行自适应调节,所以会导致训练所得的初始网络结构较大,而且没有充分利用新增神经元的潜能,影响后继对网络裁剪的效率.
本文针对单隐层二进前馈神经网络,提出一种类似ELM学习算法但又不尽相同的高效学习算法.该算法不仅调节输出层神经元的权值,同时也会调节隐层神经元权参数,它的合理性从理论上可解释为:隐层通过增加神经元个数将网络输入向高维空间映射,使得隐层输出更容易线性可分,从而方便输出层的分类,并且在增加隐层神经元个数的同时,对隐层神经元权参数进行适当调节,使得训练所得的网络结构不至于过大,从而提高裁剪的效率.
本文学习算法具有以下创新:1)能使网络在较小的结构内快速满足学习精度要求;2)提出利用神经元输出对其输入扰动的敏感性打造重要性尺度,来度量网络隐层中神经元的重要性,指导裁剪网络隐层中起作用小的神经元;3)提出利用输出层神经元偏置以及适当的再学习对裁剪后网络信息丢失进行补偿.
1 BFNN模型及符号约定BFNN是一种离散型的前馈多层神经网络,由多个离散二进神经元(BN)按一定层次结构组成,用以建立输入与输出之间的映射.
BN是BFNN的基本构造元素,构成网络中的一个节点,也是BFNN最简单的形式.结构上,BN一般由输入、连接权、偏置、激活函数以及输出等几部分组成.一个BN的工作原理是把输入分量与对应权分量乘积的和,再加上一个偏置产生一个模拟量,然后送入激活函数得到一个数字输出.在本文中,输入向量表示为X=(x1, x2, …, xn)T∈{-1, 1}n,与之相关联的权记为W=(w1, w2, …, wn)T∈Rn,w0∈R表示偏置.就功能而言,BN实现了一种从输入空间到输出空间的逻辑映射关系,即f:{-1, 1}n→{-1, 1},可表示如下:

|
BFNN由多个BN神经元按一定的规则连接而成.在BFNN中,BN分层组织,每层由若干个具有相同输入的BN组成,相邻两层上的BN彼此互相连接,同层和非相邻层上的BN彼此没有连接.各层神经元的输出构成该层的输出,前层输出作为相邻后继层每个神经元的输入,第一层神经元的输入是网络输入,最后一层的输出是网络输出.为表达方便,用记号n0-n1-n2来表示单隐层BFNN,其中,n0代表输入层并指出输入维数,n1代表隐层并指出隐层神经元个数,n2代表输出层并指出输出层神经元个数.此外,用Xn×1∈Rn表示整个网络的输入,Ym×1∈{-1, 1}m表示网络的输出.
从功能上来看,BFNN通过学习机制调整自身网络参数(包括BN的权值和偏置以及网络结构)来实现给定训练样本数据中所蕴含的输入输出之间的映射关系.
2 关键技术 2.1 调权学习算法 2.1.1 调权规则在错误更正这类调权算法中,有许多权值更新规则,如Mays’,LMS以及感知机规则等.在本学习算法中,为了使当前样本的学习对权值调整的幅度尽可能小,从而减小对已有网络的破坏,采用感知机学习规则[10]进行调权.以单个BN为例,规则可表示为

|
式中:Wnew和Wold是调整后和调整前的权,γ为学习速率,t为理想输出,a为实际输出,X为输入样本.该数学式的表示为:对应当前输入样本,当实际输出与理想输出不一致时,权需要向当前输入样本的方向做适当调整.显然,这样的学习过程是一个循环迭代的过程,直至完成对当前样本的学习为止.
2.1.2 简化的MRII学习算法在文献[4]给出的MRII算法中,根据最小扰动原则,提出了以每个BN的加权和的绝对值为衡量标准的置信度概念,通过不断迭代翻转置信度最小的神经元来找到分类效果最理想的网络权值.事实上,由于置信度并不能精确地反映BN的学习对整个网络的影响,因此MRII算法会使网络学习陷入局部震荡,导致成功率不高.在本学习算法中,并不需要一个精确衡量BN的学习对于网络影响程度的度量,因为在给定结构,如果网络无法收敛,算法会自动增加隐层神经元个数,将网络输入向高维空间映射,使得隐层输出更容易线性可分,从而方便输出层的分类.因此,本算法仍采用置信度作为隐层调权的依据,但是只针对单个样本进行学习,具体学习算法如下:
1) 将样本送入网络进行计算.
2) 如果网络对当前样本的输出正确,直接退出.
3) 在隐层执行以下步骤:
① 计算隐层神经元置信度.
② 根据置信度从小到大的顺序,对隐层神经元进行排序.
③ 对排序后的神经元依次做翻转的尝试.如果这次尝试使得样本理想输出与网络输出一致,则接受这次翻转,同时退出;如果这次尝试可以降低网络的输出错误,则同样接受这次翻转尝试,转去执行步骤②;如果这次尝试,并没有降低网络的输出错误,则拒绝这次尝试,然后对置信度次小的下一个神经元进行翻转尝试.
4) 对输出层神经元进行调权,使网络输出与样本理想输出完全一致,完成网络对该样本的学习.
不难看出,以上样本学习算法的思想在于,网络首先通过调节隐层神经元权参数,以减少网络输出错误,如果在隐层无法将网络输出错误减少到零,则对输出层神经元调权直接完成对单个样本的学习.
2.2 由输入扰动引起的BN敏感性及其计算本节所定义的敏感性度量,期望它能用来反映由BN输入扰动导致的输出扰动程度.因此,此处的敏感性定义为在所有输入模式点中由输入扰动导致BN输出值发生变化的概率,表达式为
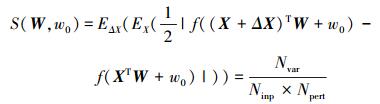
|
式中:Ninp是所有输入模式点的个数,Npert是对每个输入模式点进行扰动的次数,Nvar是所有模式点经不同扰动后输出发生变化的次数总和. ES()是将S视为统计变量求得的数学期望.如此定义的敏感性是神经元权W和偏置w0的函数,反映了BN输入的变化对输出变化的影响.由于不同的BN有不同的权和偏置值,因此敏感性可作为一个相对尺度来度量同一层中不同神经元对下一层输入的影响程度.显然,敏感性小的神经元对下一层输入的影响相对要小.
为了计算上述定义的敏感性,可先分别计算Nvar,Ninp以及Npert.设输入X∈Rn在n维空间中是均匀分布的,同时考虑到输入扰动ΔX无需太大,一次只使得输入向量中一个分量发生变化即可.因此,可以对样本输入扰动的每一个分量,在连续区间[-a, a]内以一定步长均匀离散取点,假设样本输入扰动的每一个分量以步长h在区间[-a, a]均匀取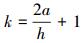
1) Nvar初始化为0.
2) 循环:对X的各种可能取值计算σ1=XTW+w0.
循环:对ΔX使得当前X只有一个分量发生变化的各种可能进行以下统计.
循环:对X发生变化的分量以步长h在区间[-a, a]的各种可能扰动计算σ2=ΔXTW.
如果σ1 < 0且σ2≥-σ1,Nvar=Nvar+1;如果σ1≥0且σ2 < -σ1,Nvar=Nvar+1.
3) 计算得出Nvar结果.
4) 计算敏感性的结果为

|
前馈神经网络结构设计仍是一个值得深入研究的问题,研究已得出结论是,网络结构在能满足训练精度前提下应尽可能的小,这样既可减少开销又可获得较好的泛化性能.裁减网络结构是获得小结构网络的一条途径,文献[11-12]综述了早前这方面的研究情况,近年提出的ELM方法中也可见到对隐层节点裁减的讨论[13].问题关键是如何建立一个能有效度量节点重要性的尺度,据此来定位网络隐层中重要性小的神经元,使得裁剪后丢失的信息尽可能的少.前面定义的BN敏感性反映了输入变化对输出的影响,当敏感性值很小时,意味输出近乎一个常量,在网络起的作用一定相对较小.注意到隐层BN敏感性只可能反映对输出层的输入影响,而输出层的输出由其输入和权值共同决定,所以敏感性还不能完全控制对输出层输出的影响,因为尽管隐层BN敏感性相对较小,乘上一个较大的输出层权值将可能放大输出层的输入变化.因此,需要将敏感性和输出层权值一起考虑,来建立对隐层BN重要性的度量.此处将BN重要性定义为BN本身的敏感性与其连接到输出层所有权值绝对值和的乘积,表达式如下:
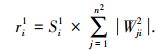
|
式中:ri1表示隐层第i个BN的重要性,Si1表示隐层第i个BN的敏感性,Wji2表示输出层第j个BN的第i个权值.
敏感性反映的是隐层中一个给定节点的输出因其输入变化而产生的变化程度,而重要性则反映的是隐层中一个给定节点对输出层节点影响的程度. ri1值越小,输出层节点受其影响就越小,因此重要性度量比敏感性度量更能反映隐层一个节点对输出层节点影响的程度.本文采用重要性尺度来裁剪隐层上的节点.
2.4 信息丢失的补偿BN的重要性尺度可用来帮助裁剪隐层上的节点.然而,训练好的BFNN网络中每个节点都会包含有用的信息,裁掉一个节点必然会引起网络信息或多或少的丢失,导致性能变差.为了弥补信息的丢失,可有以下方法对裁剪隐层节点后的网络进行补偿:
1) 调整输出层所有BN节点的偏置.设隐层上第i个BN被裁,因为重要性小的BN起着近似常数的作用,该常数可以用被裁的BN在所有训练样本输出的均值来近似表示,记为yi1,这样适当的补偿可以在输出层每一个BN上进行,将yi1乘上相应权值再加到相应的偏置上,表示如下:

|
2) 对调整后的网络,用训练样本数据再对网络进行适当的训练.
3 学习算法给出一个完整只考虑单隐层BFNN的学习算法.鉴于输入维数和输出层BN个数通常可根据应用需求确定,本算法最终给出一个隐层结构尽可能小以及确定权值的BFNN.在学习算法中,一次迭代是指训练样本集中的所有样本均输入网络完成一次学习.以下是算法的具体步骤:
1) 用预先给定的结构和随机的权值和偏置来初始化BFNN网络.
2) 在训练样本集中随机挑选一个样本,使用2.1.2给出的样本学习算法送入网络进行训练,直到样本集中的所有样本均完成一次学习(升结构阶段的一次迭代).
3) 如果在给定的迭代次数内训练的BFNN网络能够达到要求的训练精度,则停止训练,执行步骤4)开始裁剪;否则增加一个隐层节点(权值和偏置随机给出),然后执行步骤2).
4) 备份当前BFNN网络,包括它的结构以及各BN权值和偏置,并计算隐层所有节点的敏感性和重要性,试图裁掉BN重要性最小的节点.
5) 根据被裁剪掉的BN,对输出层BN的偏置进行补偿.
6) 在训练样本集中随机挑选一个样本,使用2.1.2给出的样本学习算法送入网络进行再训练,直到样本集中的所有样本均完成一次学习(裁剪阶段的一次迭代).
7) 如果在给定的迭代次数内训练的BFNN网络能够达到要求的训练精度,则停止训练,执行步骤4)继续裁剪;否则将BFNN网络恢复至之前由步骤4)所备份的结构,并给出该网络最终的权和偏置值.
4 实验验证用若干实验来验证上述BFNN学习算法的有效性.在这些实验中,需要验证以下几点:
1) 上述学习算法可以高效将BFNN网络训练到理想的精度,并且得到一个较小的网络结构.
2) 裁剪后的网络在泛化性能上要优于原来的网络.
实验以Microsoft Visual C++ 2013为平台进行,选择了三类具有代表性的问题:一是奇偶校验问题;二是针对UCI数据库中Iris数据集的分类问题;三是针对UCI数据库中Monk数据集的分类问题.为了使网络快速收敛到给定训练精度,实验中均指定样本集在某一网络结构上只进行一次迭代,如果经过该次迭代,无法达到给定训练精度,则直接增加隐层节点数,接着继续进行下一次迭代训练,如此循环往复,直至达到训练精度,之后进行裁剪.对于裁剪,设定在某一网络结构上进行迭代的最大次数为200次,如果经过200次的迭代训练,网络仍然无法达到给定训练精度,则裁剪完毕,给出网络最终的权参数.
4.1 算法高效性验证 4.1.1 奇偶校验分类实验奇偶校验是较难的线性不可分的二分类问题,它的每一个输入样本点都位于一个m维超立方的顶点.实验分别对2维、5维以及7维奇偶校验各做了10次,要求每次实验均达到100%的训练精度.使用记号m-n-l来表示m维输入,隐层含有n个节点以及输出层含有l个节点的网络初始结构.
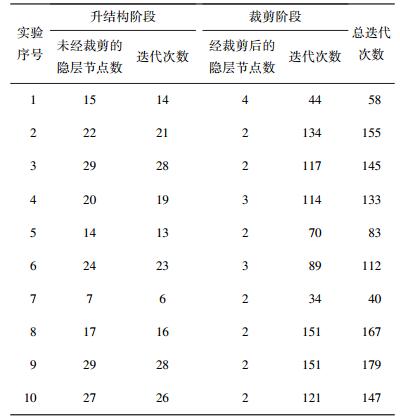
表 1~3分别记录了对2维、5维以及7维奇偶校验问题的实验结果,表明算法可以用较少迭代达到100%训练精度,并同时将网络裁剪到一个较小的结构.
| 表 1 针对2维奇偶校验本文算法实验结果(网络初始结构2-2-1) |
| 表 2 针对5维奇偶校验本文算法实验结果(网络初始结构5-5-1) |
| 表 3 针对7维奇偶校验本文算法实验结果(网络初始结构7-7-1) |
UCI数据库中的Iris数据集[13]为三分类问题,共含150个样本,4维输入.实验中用4-2-2结构作为网络初始结构,进行10组实验,当网络训练到98%以上的精度后,开始裁剪,并保证裁剪后的精度仍然为98%以上.实验结果如表 4所示,表明算法可以保证在达到给定精度的情况下,同时将网络裁剪到一个较小的结构.
| 表 4 针对Iris数据集本文算法实验结果(网络初始结构4-2-2) |
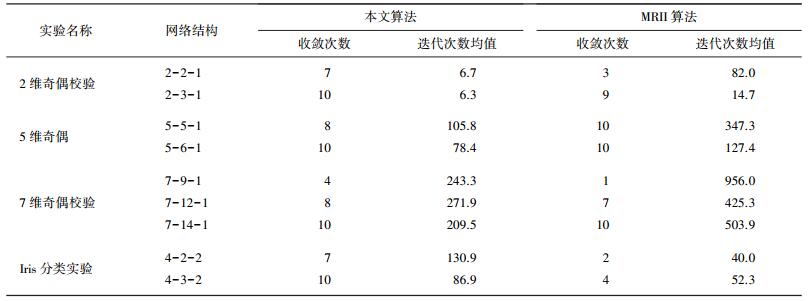
为了验证本文算法的高效性,对传统的MRII学习算法与本文算法做了完整的对比实验.对固定网络初始结构的BFNN随机给定初始权值与偏置,分别使用本文算法与MRII算法各做10组实验,记录下网络收敛次数以及收敛所需的迭代次数均值.由于MRII不具备调整网络结构的能力,因此其网络初始结构即为最终结构;而本文算法会在网络初始结构的基础上增加隐层节点个数,达到所需精度后进行裁剪,如果经裁剪后的网络隐层节点个数不大于网络初始结构,则视为收敛,并且记录网络裁剪到初始结构隐层节点数时所需的迭代次数. 表 5分别记录了本文算法与MRII算法对于2维、5维、7维奇偶校验以及Iris数据集的分类实验对比结果.其中,奇偶校验实验的最大迭代次数为1 000次,所需达到的训练精度为100%,Iris数据集分类实验的最大迭代次数为500次,所需达到的训练精度为98%.如果达到最大迭代次数,网络仍然无法训练到给定精度,则视为不收敛.
| 表 5 本文算法与MRII算法实验对比结果 |
从结果对比中不难看出,对于同一网络结构,多数情况下本文算法相比MRII收敛率更高,并且可以用更少迭代达到给定训练精度. MRII算法的实验结果好坏特别依赖于初始权值的给定,如果初始权值给的不好,那么MRII算法极易陷入局部震荡,从而需要较多的迭代次数来进行网络的训练,甚至很可能无法收敛,这一点在网络结构较小的时表现更为明显.而本文算法分为升结构与裁剪结构两个阶段,在升结构阶段为了将BFNN训练至给定精度,算法使BFNN从一个小结构网络通过逐渐增加隐层神经元个数升至一个大结构网络,因此算法收敛速度与成功率对于初始网络给定的权值依赖较小并且一定可以收敛.例如,在Iris分类实验中,可以明显看出MRII算法的实验结果好坏依赖于初始权值给定的好坏,如果初始权值给定的好,那么以较少的迭代次数就可使网络收敛,但是如果初始权值给的不好,那么很可能无法收敛.从表 5可以看出,多数情况下MRII算法在Iris数据集上达到最大迭代次数后仍然无法收敛,而本文算法基本稳定在100次左右迭代即可收敛.
4.2 算法泛化性能验证使用UCI标准样本库中的Monk分类问题中的一个数据集Monk1来进行实验验证. Monk1问题为两分类问题,共含124个样本,6维输入.实验中网络的初始结构为6-2-1,当网络训练精度达到100%后,开始裁剪,经过裁剪和补偿后,仍然保证精度为100%.使用Monk1问题来验证裁剪对网络泛化率的影响.在每一次实验中,将Monk1样本集随机划分成60%的训练样本集与40%的测试集.将训练样本集训练到100%的精度后,分别统计未经裁剪与经过裁剪后网络对于测试集的泛化率.同之前的奇偶校验与Iris实验一样,为了快速收敛到所需精度,算法在升结构阶段在某一网络结构只进行1次迭代,如果达不到训练精度,直接升隐层节点,因此在裁剪前通常会获得较大的网络结构.但可以通过在裁剪阶段进行较多次数的迭代学习,来减小网络规模.实验结果如表 6所示,多数经过裁剪后的较小结构网络比起未经裁剪的网络有着更好的泛化率.
| 表 6 Monk实验(网络初始结构6-2-1) |
本文给出一种带结构调整的高效单隐层BFNN学习算法,解决了长期以来BFNN没有高效学习算法的难题.该算法能自适应调节隐层结构并同时对隐层以及输出层神经元的权参数进行调整,在满足给定训练精度的前提下通过打造BN重要性尺度尽可能地裁剪隐层BN,使网络具有较小的结构.通过处理难度大的奇偶校验问题以及UCI数据集里的真实问题,验证了算法的可行性和有效性.
| [1] |
ZHONG Shuiming, ZENG Xiaoqin, LIU Huiyi, et al. Approximate computation of Madaline sensitivity based on discrete stochastic technique[J]. Science China:Information Science, 2010, 53(12): 2399-2414. DOI:10.1007/s11432-010-4122-6 |
| [2] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back propagation errors[J]. Nature, 1986, 323(9): 533-536. |
| [3] |
RUMELHART D E, MCCLELLAND J L. Parallel distributed processing:explorations in the microstructure of cognition[M]. Cambridge: MIT Press, 1986.
|
| [4] |
WINTER R, WIDROW B. Madaline rule Ⅱ: a training algorithm for neural networks[C]//IEEE International Conference on Neural Networks. San Diega: IEEE Publishrs, 1988: 401-408.
|
| [5] |
WINTER R. Madaline rule Ⅱ: a new method for training networks for BNs[D]. Stanford: Standford University, 1989.
|
| [6] |
张军英, 许进. 二进前向人工神经网络理论与应用[M]. 西安: 西安电子科技大学出版社, 2001: 157-168.
|
| [7] |
HUANG G B, ZHU Q, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]//Proceedings of the IEEE International Joint Conference on Neural Networks. [s. n. ]: IEEE, 2004: 985-990.
|
| [8] |
HUANG G B, ZHU Q, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489-501. |
| [9] |
HORNIK K, STINCHCOMBEA M, WHITE H. Miltilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359-366. DOI:10.1016/0893-6080(89)90020-8 |
| [10] |
MARTIN T H, HOWARD B D, MARK H B. Neural Network Design[M]. Beijing: China Machine Press, 2002: 24-27.
|
| [11] |
REED R. Pruning algorithms-a survey[J]. IEEE Transactions on Neural Networks, 1993, 4(5): 740-747. DOI:10.1109/72.248452 |
| [12] |
ENGELBRECHT A P. A new pruning heuristic based on variance analysis of sensitivity information[J]. IEEE Transactions on Neural Networks, 2001, 12(6): 1386-1398. DOI:10.1109/72.963775 |
| [13] |
MICHE Y, SORJAMAA A, BAS P, et al. OP-ELM:optimally pruned extreme learning machine[J]. IEEE Trans on Neural Networks, 2010, 21(1): 158-162. |
 2016, Vol. 48
2016, Vol. 48