2. 清华大学 机械工程系, 100084 北京
2. Department of Mechanical Engineering, Tsinghua University, 100084 Beijing, China
CO2气体保护焊因其生产效率高、操作简单、成本低、焊接质量好等特点,在汽车制造、船舶制造、金属结构及机械制造等方面得到广泛的应用[1].对直接影响焊缝成形和接头质量的熔滴短路过渡和熔池动态行为开展深入研究,具有重要的现实意义和工程应用价值.
焊接过程的熔滴过渡和熔池动态行为复杂,严重影响对其进行有效的观测和控制,促使很多学者采用数值模拟手段对其进行研究[2-8].但现有数值模拟研究很少涉及短路过渡CO2焊接熔池动态行为,这与熔滴短路过渡行为随机性强、熔池动态行为复杂、数学建模存在较大难度有关.本文充分考虑了短路过渡CO2焊接熔滴过渡行为的随机性,在建立熔滴短路过渡行为模型和熔池三维瞬态模型的基础上,对熔池的三维瞬态温度场和流场及其演变进行了数值模拟研究,并在前期的研究基础上分别针对等速送丝焊接系统和脉冲送丝焊接系统进行分析,对熔滴短路过渡间隔时间的概率密度分布、焊缝成形的数值模拟结果进行了试验验证.
1 熔滴短路过渡行为模型假设带有一定热焓和动量的熔滴在特定时刻进入熔池,对熔池的能量和动量产生影响.熔滴与熔池短路时刻、熔滴温度和体积等与熔池状态及焊接工艺参数有关.
为简化建模和计算,假设:1)熔池液态金属为粘性不可压缩流体;2)熔滴短路过渡行为的随机性主要体现在熔滴体积、温度及其与熔池短路时刻上.
1.1 熔滴与熔池短路时刻熔滴和熔池是否发生短路与前一次短路过渡结束后的初始弧长和熔滴大小、焊丝送进速度、焊丝熔化、熔滴长大以及熔池的振荡行为等因素有关.采用高速摄像拍摄熔滴图像,对典型短路过渡周期内燃弧阶段的熔滴直径最大值进行测量,可获得如图 1所示的多个短路过渡周期的熔滴直径最大值随时间变化规律,其线性拟合公式为
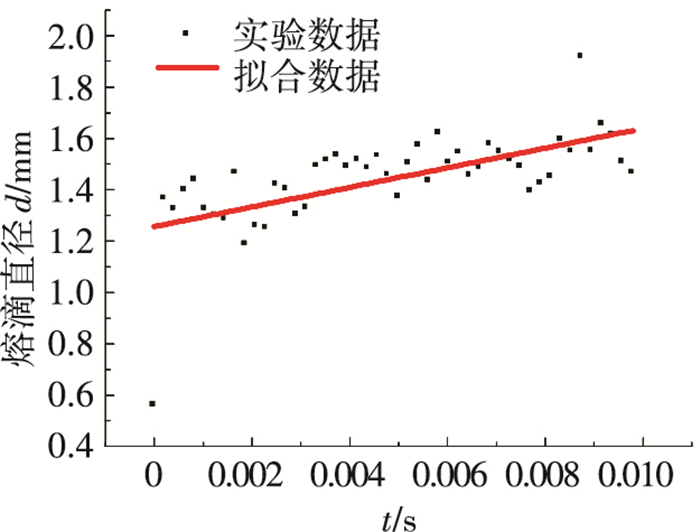
|
(焊接电流:110 A,电弧电压:14 V) 图 1 短路过渡焊接的熔滴直径最大值随时间变化规律 |
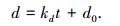
|
(1) |
式中:d为熔滴直径最大值,mm;kd为直线斜率,即熔滴长大速度,mm/s;d0为前一次短路过渡结束后的熔滴直径的初始值,mm.
由图 1和式(1)可知,熔滴长大速度kd近似与焊接电流成正比.假设燃弧初期的弧长为ld(前一次短路过渡结束时,熔滴和焊丝轴线下方熔池最高点的距离),在焊丝持续送进、熔化和熔滴长大及熔池振荡等因素的共同作用下,熔滴和熔池再次发生短路,何时发生短路可根据下式进行判断:
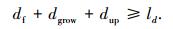
|
(2) |
式中:df为焊丝的送进距离,dgrow为熔滴长大引起的位移,dup为熔池最高点相对前一次短路结束时的最高点向上的位移.
式(2)考虑了熔池振荡的影响,从而使特定焊接工艺规范下的熔滴与熔池短路时刻具有了随机性,贴近实际短路过渡焊接过程.
1.2 短路时刻的熔滴半径对于稳定的焊接过程,焊丝送进速度等于焊丝熔化速度,即
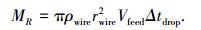
|
(3) |
式中:Vfeed为焊丝送进速度,rwire为焊丝半径,ρwire为焊丝密度,Δtdrop为短路间隔时间,MR为单个周期内的焊丝熔化量.
假设熔滴形状为规则的球缺(见图 2),则由式(3)可求出熔滴半径rdrop与Δtdrop之间满足

|
图 2 熔滴形状 |
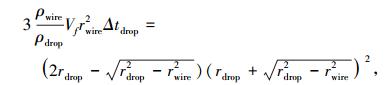
|
式中ρdrop为熔滴的密度.
由于短路间隔时间Δtdrop具有随机性,于是短路时刻的熔滴半径rdrop也具有随机性.
1.3 短路时刻的熔滴温度短路时刻的熔滴温度由熔滴热焓和比热确定:

|
式中:Tdrop为短路时刻的熔滴温度,Hd为温度为Tdrop的熔滴热焓,H1为温度为T1时的低碳钢热焓值,Cdrop为熔滴比热.
文献[9]给出了低碳钢熔滴热焓与焊接电流的关系数据,结合低碳钢比热随温度的变化曲线,可获得熔滴温度Tdrop与焊接电流I的近似表达式为

|
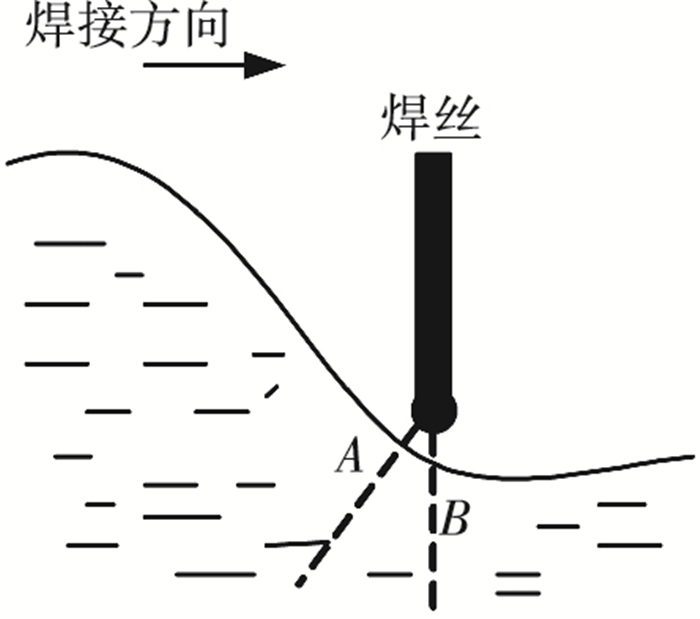
短路行为往往发生在熔滴与熔池距离最小处,如图 3中的A点.然而,寻找A点将涉及对区域内所有单元的遍历,将消耗大量计算时间.实际焊接时,熔滴短路前的熔池表面曲率半径较大,因此为了减少计算量、提高运行速度,短路点近似采用焊丝轴下方的B点,按如下步骤给出:
|
图 3 熔滴与熔池短路位置 |
1) 求出焊丝轴线下方熔池的最高点;
2) 加上熔滴半径即得到熔滴中心位置.
2 熔池热力模型建立熔滴短路过渡行为模型之后,进一步建立熔池热力模型,包括焊接热源模型,与熔池热力行为有关的动量源项、液面追踪、液态金属凝固处理.
2.1 焊接热源模型对典型短路过渡CO2焊接高速摄像进行观察发现,电弧形态沿焊接方向具有非对称性.因此,采用非对称高斯热源模型,电弧热流密度q(x, y)的表达式为
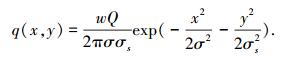
|
式中:Q为电弧功率;σs为电弧中心截面上的电弧半宽度;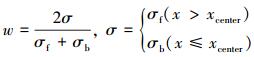
非对称高斯热源的具体参数σs、σf和σb通过测量高速摄像的电弧形状和尺寸近似确定. 图 4给出了非对称高斯热源参数和电弧尺寸之间的关系示意图.

|
图 4 非对称高斯热源模型参数确定示意 |
通过图 4测得焊丝直径在图中的长度D值以及图中的电弧前部尺寸Lf和电弧后部尺寸Lb,可以得到σf和σb的大小和相互关系,计算过程中假设σs和σf相等.
M.Lu和S.Kou通过实验测定了焊接电流与高斯热源参数之间关系[10],具体应用到CO2短路过渡焊接并参考该关系时,通过添加校正系数k进行校正:

|
通过已知焊接电流大小的高速摄影,即可以求出相应的k值.
2.2 熔池热力行为处理方法CO2气体保护焊焊接熔池的主要作用力如图 5所示. Parc为电弧压力,体现了电弧对熔池的作用力,主要方向向下;Pd为熔滴对熔池的冲击力,熔滴过渡进入熔池时,将对熔池造成较大冲击,它和电弧压力引起熔池的下凹变形;σ1和σ2分别为熔池的下表面和上表面张力,平焊时,熔池的上表面下凹,下表面下凸,表面张力均存在方向向上的分量,防止熔池下漏;Gpool为熔池中液态金属所受的重力,平焊时,重力是引起熔池下塌的因素之一;τ为等离子流产生的熔池表面剪切力,造成熔池表面的液态金属以焊丝轴线为中心向四周流动;N为周围坡口“壁面”的支撑力,也是方向向上的作用力.需要注意的是,由于母材的熔化,此时的“壁面”是固液界面动态分界线(省略糊状区).
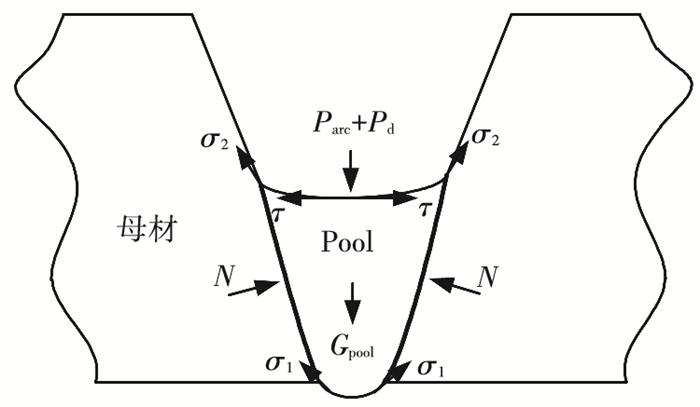
|
图 5 熔池受力示意 |
对熔池所受各种作用力、液面追踪、液态金属凝固分别采用如下处理方法:
1) 对熔池所受各种作用力产生的动量源,采用附加源项法进行处理.充分考虑熔池表面温度和张力分布不均匀引起的液体金属Marangoni流,由连续表面张力模型CSF[11],结合散度定理,求出表面张力源项;采用Boussinesq近似假设处理热浮力;电弧压力参考文献[12];假设自由表面的电流密度符合高斯分布,再结合电磁场的Maxwell方程组、欧姆定律等推导出三个方向电磁力源项.
2) 对于熔池自由表面(气-液界面),充分考虑熔池的上下表面变形,采用VOF模型进行跟踪,通过控制流体体积分数函数来获取自由面.
3) 对于熔池凝固过程,采用液相体积分数法处理凝固潜热问题,采用焓-孔隙度法[13]来处理糊状区的动量损失.
3 数值模拟结果及分析在前述基础上,运用有限体积法,基于Fluent软件UDF功能二次开发,模拟短路过渡CO2焊接的熔池动态行为及三维瞬态温度场.
采集焊接过程中的焊接电流和电弧电压数据,采用MATLAB和C语言混合编程进行统计分析.数据采集装置如图 6所示,高速PCI采集卡有4个通道,每个通道采样频率为2.5 MHz.
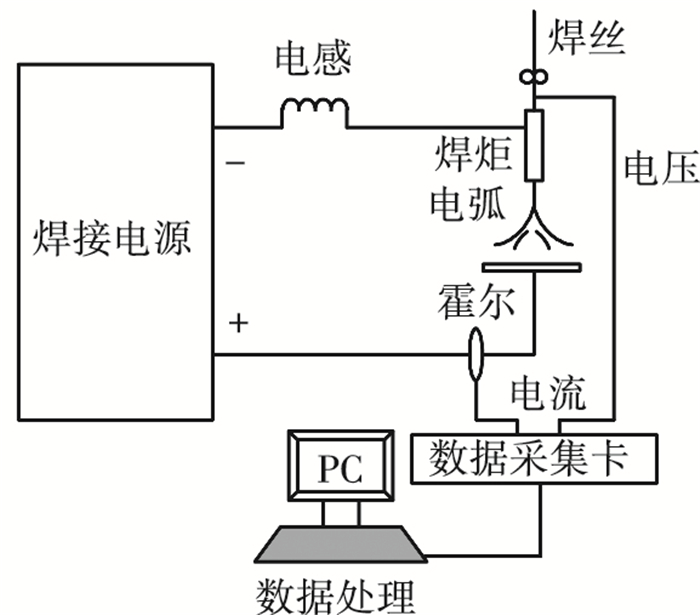
|
图 6 数据采集装置示意 |
焊接实验条件为:纯CO2气体保护,流量为10 L/min;焊丝直径1.2 mm,牌号为H08Mn2SiA.单边工件尺寸为330 mm(长)×60 mm(宽)×6 mm(厚),装配间隙1.6 mm,钝边1 mm,V型坡口的单边角度30°,送丝速度1.45 m/min.
为提高计算速度,建立半模型,截除对计算结果影响较小且远离焊缝的母材下方的气相区域;主要计算域示意图如图 7所示(40 mm(长)×8 mm(宽)×6 mm(厚), 下部存在8mm(宽)×2 mm(高)气体层).
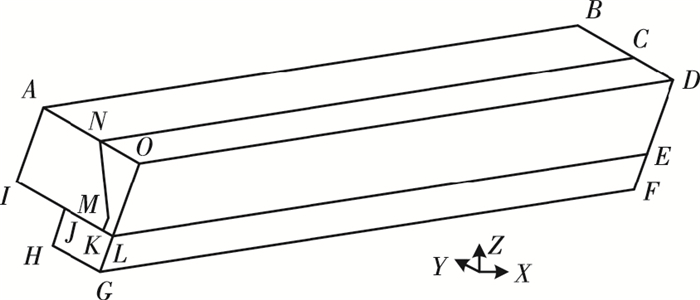
|
图 7 计算域示意 |
图 7中,以ANMKI为截面的实体为第二相域,其余为气相域(主相). NOCD为气相入口,两侧面NOLKM等为气体出口,ODEFGL为中心对称面.熔池上下表面、母材上下表面、处于熔池上方的坡口壁面等,为对流和辐射散热.中心对称面为绝热边界,即
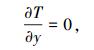
|
中心对称面的动量边界条件为

|
(10) |
熔池上表面的自由表面的连续性条件为

|
(11) |
在固相/气相界面上有:u=0, v=0, w=0. 为提高计算收敛性,采用六面体划分网格,采用自适应时间步长进行计算.随温度变化的材料属性详见文献[14-15].
3.1 熔池瞬态流场和温度场模拟结果表明,大约在焊接开始后的0.2 s,熔池开始形成;2 s左右,熔池达到宏观准稳定状态. 1.5103 06 s和2.014 17 s时的熔池流场和温度场瞬态分布如图 8所示.
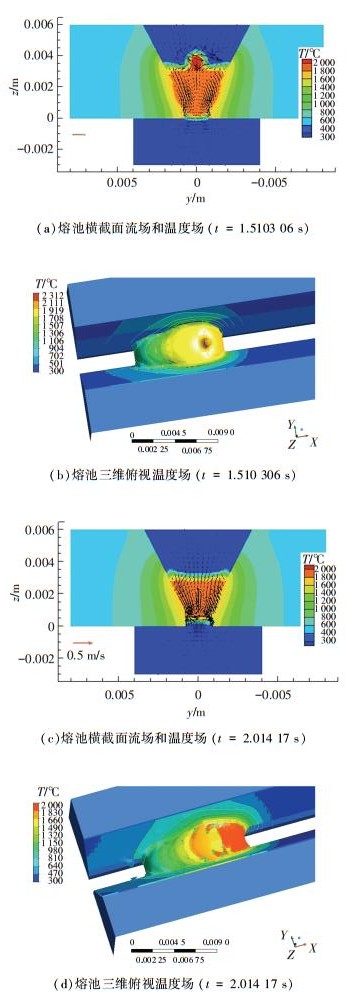
|
图 8 熔池温度场和流场的瞬态分布 |
由图 8(a)可见:在1.510 306 s这一时刻,熔滴正向熔池过渡,熔滴温度最高;由于熔滴向熔池过渡存在的液态金属运动,其附近流速较大,同时,熔池液态金属在坡口侧壁处的流向指向坡口壁面,有利于增大熔合比.图中的矢量箭头表示流体流动方向和大小,可以看到此时由于熔滴正向熔池过渡使得熔滴周围流体速度最大.
图 8(c)~(d)的2.014 17 s时刻,熔滴已完成向熔池的过渡,熔池温度相对均匀,熔池下部的液态金属由于熔滴向下的冲击使得其流动更强烈.
3.2 熔滴短路过渡频率在短路过渡CO2焊接中,熔滴和熔池的短路时刻和短路过渡频率存在随机性. 图 9所示为等速送丝焊接时的熔滴短路间隔时间的概率密度分布的实验值和数值模拟结果对比.
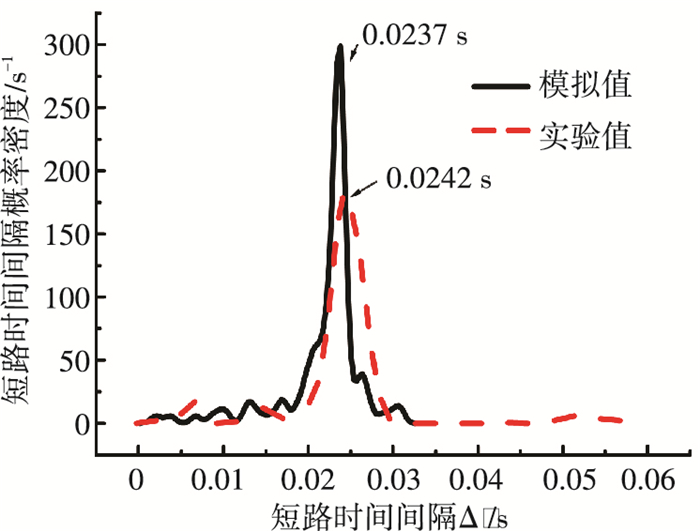
|
图 9 等速送丝焊接短路间隔时间概率密度分布 |
由图 9可以看出:数值模拟获得的短路间隔时间概率密度在23.7 ms处达到峰值,熔滴短路过渡频率约为42 Hz;而实验获得的短路间隔时间概率密度在24.2 ms处达到峰值,熔滴短路过渡频率约为41 Hz,两者偏差仅2.1%.由于焊接实验过程不可避免地会受到其他随机因素(如焊接电源输出电压和焊丝送进速度波动等)的影响,因而获得的短路间隔时间概率密度峰值所对应的范围较宽,峰值较低;而数值模拟的随机因素较少,从而峰值对应范围较窄,峰值较高.
为进一步验证熔滴短路过渡行为模型的有效性,将其应用于脉冲送丝式短路过渡CO2焊接[16]的数值模拟. 图 10为短路间隔时间概率密度分布的实验值和数值模拟结果对比结果.
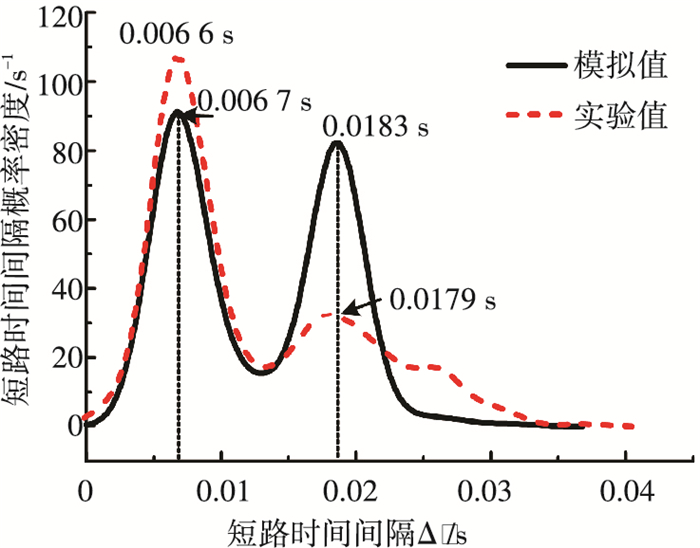
|
图 10 脉冲送丝焊接短路间隔时间概率密度分布(峰值送丝速度为3.2 m/min,基值送丝速度为1.45 m/min,脉冲送丝周期为0.6 s,峰值送丝时间为0.1 s,基值送丝时间为0.5 s,坡口装配间隙为1.6 mm) |
由图 10可以看出:由于脉冲送丝时的峰值送丝速度和基值送丝速度相差较大,熔滴短路间隔时间的概率密度分布与等速送丝时的单一峰值存在明显差异,峰值送丝速度和基值送丝速度分别对应不同的熔滴短路间隔时间,数值模拟结果呈现明显的“双峰”分布. 图 10的左侧峰值对应峰值送丝速度,短路间隔时间的模拟值约为6.7 ms、实验值约为6.6 ms,熔滴短路过渡频率分别为149、151 Hz,二者相差仅1.5%;图 10的右侧峰值对应基值送丝速度,短路间隔时间的模拟值约为18.3 ms、实验值约为17.9 ms,熔滴短路过渡频率分别为54、55 Hz,二者相差2.2%.
固定峰值送丝时间为0.2 s、基值送丝时间为0.5 s、基值送丝速度为1.45 m/min,改变峰值送丝速度,分别为2.6、3.2和5.0 m/min. 图 11为不同峰值送丝速度下的熔滴短路间隔时间概率密度分布. 3种条件下,对应基值送丝速度的短路间隔时间概率密度峰值所对应的时间基本一致,分别为18.37、18.43和18.59 ms,熔滴短路过渡频率分别为54.4、54.3、53.8 Hz,相对均值的误差分别为0.5%、0.2%和0.7%,即基值送丝速度不变,对应的熔滴短路过渡频率也基本不变;而对应峰值送丝速度的短路间隔时间概率密度峰值所对应的时间分别为7.27、6.5和7.58 ms,熔滴过渡频率分别为137、153、131 Hz.可见,熔滴短路过渡频率并不是随着送丝速度增大而单调增加,而是在一定范围内存在一个最高值.
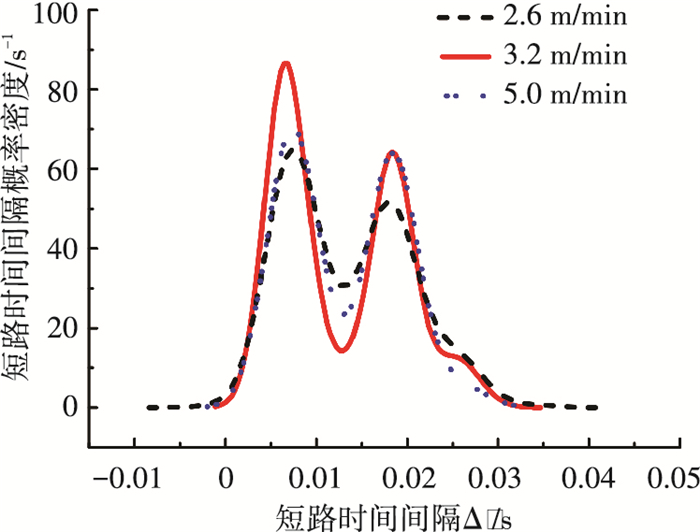
|
图 11 不同峰值送丝速度时的短路间隔时间概率密度分布 |
图 12所示为数值模拟获得的焊缝背面温度场分布及相同条件下实验获得的焊缝背面外观成形.由图 12(a)可以看出,在熔池底部低于固相线温度(1 773 K)的区域未超过母材底部,完全冷却后将形成焊缝背面未熔合.数值模拟和实验结果吻合较好.
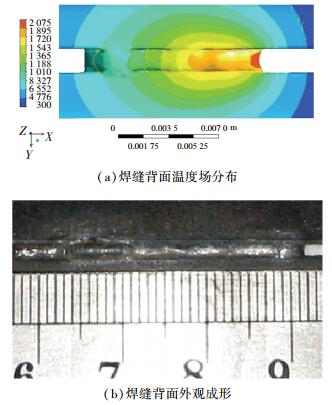
|
图 12 焊缝背面温度场分布和外观成形 |
图 13为数值模拟获得的焊缝横截面(浅色区域为母材及凝固后的焊缝横截面, 深色为气相域)与相同条件下实验获得的焊缝横截面对比.可以看出,数值模拟获得的焊缝背面余高和正面焊缝高度基本吻合,证明了所建数学模型的有效性.

|
图 13 焊缝横截面的数值模拟和实验结果对比(峰值送丝速度为3.2 m/min,基值送丝速度为1.45 m/min,脉冲送丝周期为0.6 s,峰值送丝时间为0.1 s,基值送丝时间为0.5 s,坡口装配间隙为1.6 mm) |
1) 可通过熔滴与熔池短路时刻、短路时刻熔滴半径、温度等因素表征CO2焊接熔滴短路过渡的强随机性.
2) 文中所述的等速送丝条件下大约在焊接开始后的0.2 s,熔池开始形成;2 s左右,熔池达到宏观准稳定状态, 送丝速度1.45 m/min时焊缝背面未熔合; 熔滴短路过渡频率并不是随着送丝速度增大而单调增加,而是在一定范围内存在一个最高值.
3) 实时获取熔池流动状况较为复杂,可通过焊后的焊缝背面成形和横截面形状对比以及在连续送丝和脉冲送丝条件下短路间隔时间概率密度分布对比验证所建立的数学模型,计算得到的连续送丝条件下短路间隔时间概率密度分布呈单峰特征,而脉冲送丝条件下为明显的双峰特征.
4) 该数学模型不仅适用于传统的等速送丝系统,而且适用于脉冲送丝式的短路过渡焊接熔池模拟.
| [1] |
周培山, 谢芋江, 杨昕, 等. 不同CO2气保焊工艺对Q345钢焊接接头的影响[J]. 电焊机, 2014, 5(44): 213-216. |
| [2] |
OREPERA G M, SZEKELY J. Convection in arc weld pool[J]. Welding Journal, 1983, 62(11): 307-312. |
| [3] |
THOMPSON M E, SZEKELY J. The transient behavior of weld pools with a deformed free surface[J]. International Journal of Heat and Mass Transfer, 1989, 32(6): 1007-1019. DOI:10.1016/0017-9310(89)90003-3 |
| [4] |
KO S H, YOO C D, FARSON D F, et al. Mathematical modeling of the dynamic behavior of gas tungsten arc weld pools[J]. Metallurgical and Materials Transactions B, 2000, 31(6): 1465-1473. DOI:10.1007/s11663-000-0031-1 |
| [5] |
ITO M, IZAWA S, FUKUNISHI Y, et al. SPH simulation of gas arc welding process[C]//Seventh International Conference on Computational Fluid Dynamics (ICCFD7). Hawaii: Springer, 2012.
|
| [6] |
赵明, 武传松, 赵朋成. GTAW熔池形状数值模拟精度的改进[J]. 焊接学报, 2006, 27(3): 17-20. |
| [7] |
孙俊生, 武传松. 电弧热流分布模式对GMAW焊接温度场的影响[J]. 焊接学报, 1998, 19(4): 255-260. |
| [8] |
饶政华. 熔化极气体保护焊传热与传质过程的数值研究[D]. 长沙: 中南大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1721761
|
| [9] |
曹振宁. TIG/MIG焊接熔透熔池流场与热场的数值分析[D]. 哈尔滨: 哈尔滨工业大学, 1993.
|
| [10] |
LU M, KOU S. Power and current distributions in gas Tungsten arcs[J]. Welding Journal, 1988, 67(2): 29-34. |
| [11] |
BRACKBILL J U, KOTHE D B, ZEMACH. C. A Continuum method for modeling surface tension[J]. Journal of computational physics, 1992, 100: 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [12] |
安藤弘平, 长谷川光雄. 焊接电弧现象[M]. 施雨湘, 译. 北京: 机械工业出版社, 1985: 16.
|
| [13] |
VOLLER V R, BRENT A D, PRAKASH C. The modeling of heat, mass and solute transport in solidification systems[J]. International Journal of Heat and Mass Transfer, 1989, 32(9): 1719-1731. DOI:10.1016/0017-9310(89)90054-9 |
| [14] |
TOULOKIAN Y S. Thermal physical properties of matter[M]. New York: IFI/Plenum Press, 1970.
|
| [15] |
SCHNICK M, WILHELM G, LOHSE M, et al. Three-dimensional modelling of arc behavior and gas shield quality[J]. Journal of Physics D:Applied Physics, 2011, 44(18): 1-25. |
| [16] |
夏胜全, 区智明, 孙晓明. 脉冲送丝式CO2短路过渡焊及焊缝背面成形控制[J]. 电焊机, 2013, 43(12): 9-13. |
 2016, Vol. 48
2016, Vol. 48


