基本遗传算法(SGA)是一类模拟生物进化的智能优化算法,已广泛应用于工程领域的优化求解.但大量实践和研究表明,基本遗传算法存在全局搜索能力差和早熟收敛等问题,被称为基因漂移[1].针对这一问题, 学者提出了各种小生境遗传算法(NGA),但这些经典的小生境技术均存在参数设置问题[2-5].这些参数的预设与优化需要一定的先验知识,处置不当将难以维持稳定的小生境,从而限制了算法的有效运用.
本文基于可拓理论[6]和全局性优化考虑,提出可拓聚类适应度共享小生境遗传算法(ECNGA).算法基本原理为:构造可拓遗传算法模型,提出遗传信息物元编码和可拓遗传算子;利用可拓聚类方法对每代种群划分形成小生境群体;根据适应度共享机制调整个体适应度,再种群进化,并结合聚类小生境的代表个体保存策略,维持小生境的稳定性和多样性,从而有效地防止算法早熟收敛, 增强全局搜索能力.
1 可拓聚类分析定义1 设聚类Hp={R1, R2, …, Rnp},类内样本个体的物元模型[6]为

|
对i=1, 2, …, m,各物元特征Ci的属性值分别为v1iv2i…vnpi.令
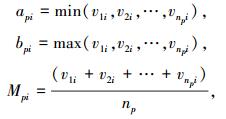
|
称类Hp各特征属性取值区间为Vpi(Cpi)=[api, bpi].
定义Rp为类Hp的中心物元,记为
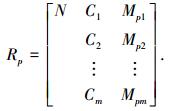
|
若np=1时,令Vpi(Cpi)=[ai, bi],即各特征属性取值为节域区间,同时令中心物元为Rp=R1.
1) 已知类Hp={R1, R2, …, Rnp},取待聚类样本Rx=[N, C, V],样本的m维特征观测值为V=(x1, x2, …, xm)T.
2) 对类Hp,计算Rx各特征属性xi的基本关联函数为

|
3) 计算综合关联度Kx(Hp).若规定各项聚类特征的权重系数为λp=[λp1, λp2, …, λpm],则

|
权重系数表示各项特征在聚类评价体系中的相对重要程度,可采用专家评价法、层次分析法或比重权数法确定[7].
关联度Kx(Hp)表示样本Rx与类Hp={R1, R2, …, Rnp}的关联程度,其取值大小是判定样本是否归属该类的直接依据.
可拓聚类方法的基本流程如下:
Step 1 按照聚类样本的指标或维数建立物元模型为

|
令
Step 2 初始化聚类.将待聚类物元按某种规则排序(例如遗传优化的适应度排序),并产生一随机数k(1 < k < n),取前k个物元形成k个初始类.
Step 3 依次取剩余样本Rx,计算Rx对类Hp(p=1, 2, …, k)的关联度Kx(H1), Kx(H2), …, Kx(Hk).
Step 4 判定待聚类样本Rx的类属.令Kx(Hq)=max{Kx(H1), Kx(H2), …, Kx(Hk)}.若Kx(Hq)>0,则Rx属于类Hq;Kx(Hq)=0,可认为Rx属于或不属于类Hq;Kx(Hq) < 0,Rx不属于已知类,需增加新的聚类,即设样本Rx为新类别,聚类数目k=k+1.
Step 5 调整新增样本的类Hq或新增类的属性取值区间、中心物元,并求平均关联度. Hq类内平均关联度记为
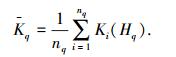
|
式中,nq是Hq类内样本数目,Ki(Hq)是类内第i个样本的关联度.
Step 6 类属约简.取类Hq的中心物元Rq,计算Rq对所有类Hp的关联度Kq(Hp)(p=1, 2, …, k, p≠q). Kq(Hp)表示类Hq、Hp之间的相似性.若Kq(Hp)≥Kp,表示两个类属相似度较强,可合并为一个类,聚类数k=k-1,并计算约简后的取值区间、中心物元及平均关联度.
Step 7 跳转Step3,处理所有待聚类的n-k个样本物元.
Step 8 聚类检验.
1) 对类Hp(p=1, 2, …, k), 计算并固定中心物元Rp;
2) 计算所有物元Rx对所有类的关联Kx(Hp)(x=1, 2, …, n, p=1, 2, …, k);
3) 令Kx(Hq)=max{Kx(H1), …, Kx(Hk)},聚类样本Rx归属至类Hq;
4) 循环以上3步,直至所有样本个体的聚类归属不变.
Step 9 输出聚类结果,包括聚类数目k,每一个聚类Hp下的样本数np,及类内样本关于该聚类的关联度Kx(Hp).
定义3 若样本集合X(t)有k个聚类,X(t)={H1, H2, …, Hk},各聚类样本数目为(n1, n2, …, nk),集合总样本数目
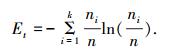
|
熵是反映集合内样本聚类多样性程度的重要指标.
2 可拓聚类适应度共享小生境遗传算法 2.1 DNA编码物元定义4 设遗传信息为物元的集合,记为Ri=[N, C, V].基因特征属性Cj(j=1, 2, …, m)的量值为vij,其定义域Vj=[aj, bj].
将属性量值用遗传算法编码(l1, l2, …, lt)表示,则每项特征所对应的编码为
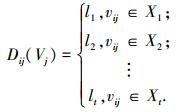
|
式中, X1, X2, ….Xt为在[-∞, +∞]的t个区间.
经过量值编码后,将遗传信息物元扩展定义为DNA编码物元[7],记为
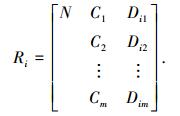
|
定义5 设DNA编码物元R0∈R,将R0改变为另一个同类DNA编码物元或多个同类编码物元的可拓变换,称为R0的可拓遗传算子,记作

|
可拓遗传算子可用事元[6]的形式化语言表示为

|
式中,OT是动作的名称,表示实施遗传操作的类型,即

|
可拓遗传可解析为:vt4对vt1实施变换OT,变换量为vt2,变换结果为vt3.结合物元可拓变换的多种形式, 可得一些常用或特有的可拓遗传算子.
1) 复制算子(或称选择算子) T{R}={R},即

|
常用的复制选择方法有适应度比例选择法、锦标赛选择法和排序选择法.
2) 交叉算子T{R1, R2}={R′1, R′2}. 基本的有单点交叉、两点交叉、多点交叉等.
例如,父代个体{R1, R2},运用两点交叉算子,操作结果为
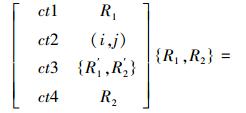
|
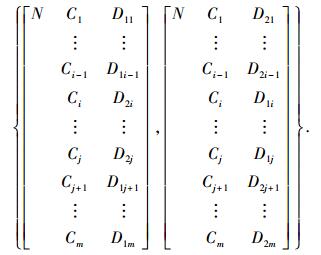
|
式中,(i, j)表示交叉的基因座位置.
若为实数编码的算术交叉算子,取随机数α∈(0, 1),则有

|
3) 置换变异算子T{R}={R′},即
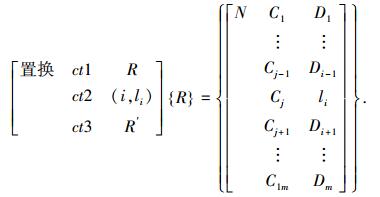
|
表示随机取基因座i(1≤i≤m),在i处以编码li替换.若为实数编码的变异算子,则可取li=Umini+r(Umaxi-Umini),其中随机数r∈[0, 1],[Umini, Umaxi]表示变异点处基因值的取值范围.
4) 扩缩算子T{R}=αR,是指扩大或缩小随机选择的基因编码的量值, 即
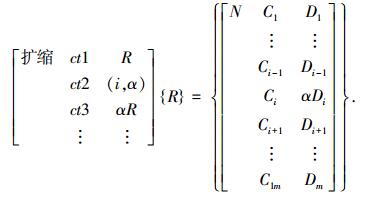
|
当α>1时为扩大算子,当0 < α < 1时为缩小算子.
5) 增删算子T{R}={R′},即
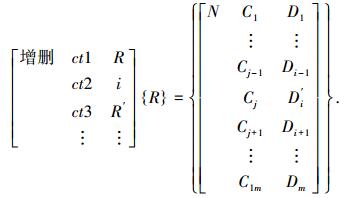
|
当D′i=Umaxi时为增加算子,当D′i=Umini时为删除算子.
2.3 小生境构造及适应度共享基于可拓聚类方法构造小生境,对个体适应度共享.其基本过程为:
1) 对每代种群X(t)进行可拓聚类.聚类数目k,每一个类Hp下的样本数np,类内样本关联度Kx(Hp).

|
式中,mi为个体i的小生境数,其值越大,表示其相似个体越多,反之越稀疏.
3) 适应度共享,调整小生境中个体的适应度为

|
式中fi、fi′分别为共享前、后的适应度.
ECNGA算法对种群聚类,并选出每类的代表个体[10]保存至下一代种群.代表个体保存策略如下:
Step 1 标记种群X(t)的聚类代表个体为{a1(t), a2(t), …, ak(t)};
Step 2 遗传生成种群X(t+1),并可拓聚类;
Step 3 取ai(t)(i=1, 2, …, k),判断其聚类归属Hp(p∈[1, 2, …, k′]);
Step 4 以代表个体替换聚类Hp中适应度最低的个体;
Step 5比较代表个体ai(t)与目前聚类中适应度最高个体的bp(t+1),若f(ai(t)) < f(bp(t+1)),则重新标记bp(t+1)为代表个体.
采用适应度共享机制和代表个体保存策略进行遗传操作,可使种群维持稳定且多样的小生境,提高算法的全局搜索能力.
2.4 交叉概率Pc和变异概率Pm为促进种群的多样性,Pc、Pm应与小生境熵Et呈负相关关系.另外,对适应度高的个体,可增大Pc以加快其进化速度,减小Pm以避免破坏其结构模式.因此,设计自适应调整Pc和Pm为
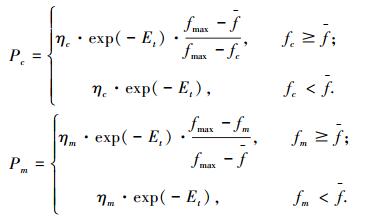
|
式中:0 < ηc < 1且0 < ηm≤1;fmax, f为每代种群中最大的适应度及平均适应度;fc为交叉两个体中较大的适应度;fm为变异个体的适应度.
2.5 ECNGA可拓小生境遗传算法流程Step 1 算法初始化,即设定种群规模n、Pc、Pm等参数和置终止准则, 随机生成初始种群X(t)={Ri, i=1, 2, …, n}, 置进化代数t←0.
Step 2 计算种群X(t)中个体适应度fi,按适应度降序排列.
Step 3 对种群X(t)={Ri, i=1, 2, …, n}进行可拓聚类,构造k个小生境.
Step 4 代表个体保存并更新标记.
Step 5 计算种群中所有个体的共享适应度fi′.
Step 6 种群进化,即可拓遗传形成种群X(t+1).
1) 可拓选择从父代X(t)中运用选择算子选择出n/2对个体.
2) 可拓交叉n/2对个体依概率Pc进行交叉,形成n个中间个体.
3) 可拓变异依概率Pm对n个中间个体变异,形成子代X(t+1).
Step 7 终止检验.若不满足终止准则,置t←t+1并跳转step2;满足时则输出种群X(t+1)中最优解.
2.6 算法收敛性分析引理1[10-11] 基本遗传算法SGA收敛到全局最优解的概率小于1.
引理2[10-11] 保留最优个体的GA算法以概率1收敛到全局最优解.
定理1 采用代表个体保存策略的ECNGA算法以概率1收敛到全局最优解.
证明 标记代表个体{a1(t), a2(t), …, ak(t)}∈X(t),令

|
即ap(t)为X(t)的最优个体.
同理,令X(t+1)的最优个体bq(t+1)=max{b1(t+1), b2(t+1), …, bk′(t+1)}.
1) 设p=q,若ap(t)>bq(t+1),则最优个体ap(t)被保存;反之即存在超过ap(t)的最优个体bq(t+1),且bq(t+1)被保存.
2) 设p≠q,ap(t)>bq(t+1),则ap(t)>bp(t+1),最优个体ap(t)在类Hp中保存;ap(t) < bq(t+1),则aq(t) < bq(t+1),最优个体bq(t+1)在类Hq中保存.
综上,采用代表个体保存策略的ECNGA算法在每代选择操作前保留最优个体,依据引理2,ECNGA算法以概率1收敛到全局最优解.
3 仿真实验及分析实验1 经典多峰Shubert函数寻优.
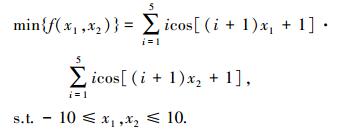
|
Shubert函数有760个局部最优点和18个全局最优点,全局最优目标函数值-186.730 9.取适应度函数为
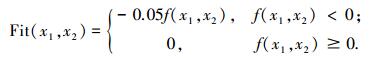
|
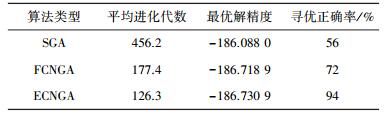
同时比较SGA、模糊聚类FCNGA[4]及ECNGA三种算法.参考文献[4]设置算法参数:每次随机产生初始种群,规模n=100,进化代数Gmax=500,交叉算子ηc=0.6,变异算子ηm=0.01,终止条件为目标函数值与当前最优解差0.1%时或进化代数达Gmax, 优化重复次数50.仿真结果如表 1所示,进化曲线图 1所示.
| 表 1 多峰函数寻优仿真结果对比 |

|
图 1 种群平均值进化曲线 |
从表 1数据及图 1进化曲线可知,ECNGA算法明显优于其他两种算法,搜索能力较强,有更高的求解质量和更快的收敛速度,并避免了出现早熟而陷入局部极值的情形.
实验2 自调整模糊控制器优化设计.
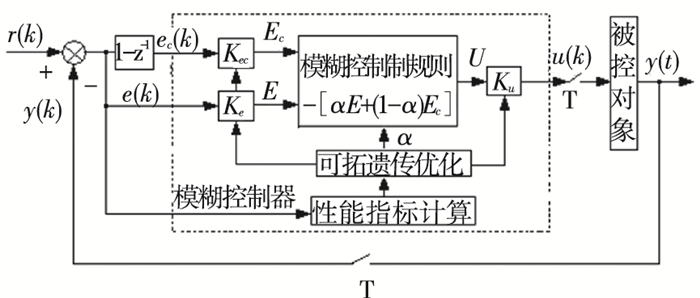
图 2所示为基于可拓遗传优化的自调整模糊控制系统结构图. 图 2中各物理量分别为系统给定值r(k)、输出响应y(k)、误差e(k)、误差变化率ec(k)及控制输出量u(k).
|
图 2 可拓遗传优化的自调整模糊控制系统结构图 |
模糊控制规则解析式为
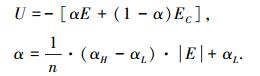
|
式中:E、EC为误差、误差变化率量化取整,U为控制量量化取整,修正因子α∈[αL, αH]且0 < αL≤αH < 1.
图 2中可拓遗传优化机构的作用是根据所选取的寻优目标函数,搜索修正因子α、量化因子Ke、Kec及比例因子Ku等复杂多维参数的全局最优解,构成最优模糊控制器.
选取ITAE作为寻优目标函数,即
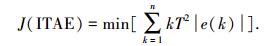
|
式中,T为采样周期,n为决定ITAE指标的总时间.
在MATLAB/SIMULINK中构建寻优模糊控制系统.设对象为多数工控过程的二阶惯性加延迟的模型:

|
设置寻优约束条件[12]为
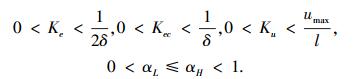
|
式中:δ为控制要求的稳态误差,取δ=0.01;umax为被控对象允许输入的最大值,仿真模块内取umax=12 V.
设优化参数编码物元R=[N C D],物元特征C=(Ke, Kec, Ku, αL, αH)T,D为对应浮点数编码.为对比观察,采用参考文献[12]的SGA方法同时参数寻优.随机生成规模n=200的初始种群,取遗传参数ηC=0.6、ηm=0.02和进化终止代数Gmax=100.
ECNGA算法寻优后获得最优控制参数为
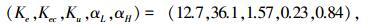
|
同等条件下,SGA算法优化参数为
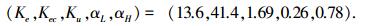
|
将两组优化参数分别代入自调整模糊控制仿真模块,即可得控制结果曲线, 如图 3、4所示.采样周期T=0.1 s.

|
图 3 正弦信号跟踪 |

|
图 4 阶跃信号跟踪 |
1) 正弦信号跟踪实验.如图 3曲线所示,点形虚线为给定信号r(t)=sin t,取ITAE控制指标总时间为50.线段虚线为SGA优化的模糊控制正弦响应曲线,其ITAE=273.1,实线为ECNGA优化后的模糊控制正弦响应曲线,其ITAE=211.5.
2) 阶跃信号跟踪实验.如图 4所示,给定阶跃信号r(t)=ε(t),10 s前为模糊控制阶跃响应上升阶段.曲线①为SGA优化参数,ITAE=11.2,稳态e(∞)=0.004 7;曲线②为ECNGA优化参数,ITAE=5.9,稳态e(∞)=-0.001 4.在30 s处施加负载扰动时,可观察优化模糊控制器能更快恢复稳定.
对比两组优化参数可知,ECNGA优化方法可获得全局最优解,其模糊控制器在信号跟踪的动静态性能方面优于SGA优化模糊控制,其响应曲线虽然稍有超调, 但调节时间大大缩短,控制精度和稳态性能也有了比较明显的改进,而且对扰动的鲁棒稳定性更好.
4 结论1) 使用可拓聚类分析对种群划分小生境, 按照共享机制对个体的适应度进行调整, 可以增大种群多样性和有效防止早熟收敛; 结合聚类代表个体保存策略, 维持稳定的小生境, 以增强全局搜索能力.
2) 引入度量种群多样性的小生境熵自动调整进化参数, 可有效平衡算法快速性和多样性的矛盾.
3) 该算法优于标准遗传算法和常规小生境遗传算法, 具有全局寻优能力和较高的搜索效率, 是一种适用于复杂寻优问题的有效优化算法.
| [1] |
玄光男, 程润伟. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004: 21-30.
|
| [2] |
CHEN C H, LIU T K, CHOU Y H. A novel crowding genetic algorithm and its applications to manufacturing robots[J]. IEEE Transactions on Industrial Informatics, 2014, 10(3): 1705-1706. DOI:10.1109/TII.2014.2316638 |
| [3] |
KIM Hyoungjin, LIOU Mengsing. New fitness sharing approach for multi-objective genetic algorthm[J]. Journal of Global Optimization, 2013, 55(3): 579-595. DOI:10.1007/s10898-012-9966-4 |
| [4] |
谭艳艳, 许峰. 自适应模糊聚类小生境遗传算法[J]. 计算机工程与应用, 2009, 45(4): 52-55. |
| [5] |
陆青, 梁昌勇, 杨善林, 等. 面向多模态函数优化的自适应小生境遗传算法[J]. 模式识别与人工智能, 2009, 22(1): 91-99. |
| [6] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014: 18-96.
|
| [7] |
王科俊, 徐晶, 王磊, 等. 基于可拓遗传算法的机器人路径规划[J]. 哈尔滨工业大学学报, 2006, 38(7): 1135-1138. |
| [8] |
赵敏, 林道荣, 瞿波, 等. 一种新的基于小生境模拟退火的遗传算法[J]. 辽宁工程技术大学学报, 2013, 32(3): 367-372. |
| [9] |
SANTRA A K., CHRISTY C. J, NAGARAJAN B. Cluster based hybrid niche mimetic and genetic algorithm for text document categorization[J]. International Journal of Computer Science Issues, 2011, 8(2): 450-456. |
| [10] |
何琳, 王科俊, 李国斌, 等. 最优保留遗传算法及其收敛性分析[J]. 控制与决策, 2000, 15(1): 63-66. |
| [11] |
LI Junhua, LI Ming. An analysis on convergence and convergence rate estimate of elitist genetic algorithms in noisy environments[J]. Optik, 2013, 124(24): 6780-6785. DOI:10.1016/j.ijleo.2013.05.101 |
| [12] |
葛平淑, 郭烈. 参数自调整的月球车路径跟踪模糊控制器设计[J]. 计算机工程与应用, 2012, 48(11): 55-59. DOI:10.3778/j.issn.1002-8331.2012.11.013 |
 2016, Vol. 48
2016, Vol. 48