近年来，大跨空间结构建造的比例不断上升，如体育馆、展览馆、以及大型装配车间等，这些建筑通常为人口密集场所，且造价高昂，为了保证人们的生命财产安全，大跨空间结构的隔震性能及措施研究显得尤为重要.摩擦摆支座(friction pendulum bearing，FPB)作为一种典型的基础隔震设备，由美国加州大学伯克利分校的Zayas等^[1]提出，它具有良好的隔震性能，具有造价低、易施工、易维护、承载力高等特点.在此基础上，许多隔震机理相近的摩擦摆支座形式得到了进一步发展，如VFPI^[2]和MFPS^[3].1997年，蔡崇兴^[4]推导了摩擦摆支座的有限元方程，并分析了其隔震机理；2005年，杨林等^[5]对安装摩擦摆支座的四层钢框架结构进行了振动台试验研究，结果表明摩擦摆支座具有良好的隔震性能.此后，许多学者对摩擦摆支座进行大量的试验和数值分析^{[6, 7, 8]}，并证明该种支座隔震设备的有效性.摩擦摆支座已在全世界数百座建筑中得到应用，如西雅图海鹰美式足球场、华盛顿州应急指挥中心等^[9].

目前，国内外学者主要关注单向地震动作用下应用摩擦摆支座结构抗震性能的研究^{[10, 11, 12]}，很少开展多维地震动作用下结构动力性能的研究.2002年，朱玉华等^[13]对应用摩擦滑移支座的三层缩尺钢框架结构进行了多维振动台试验,结果表明竖向地震动对上部结构的水平地震响应有显著影响；另外，王建强等^{[14, 15]}分析了应用摩擦摆支座的七层钢混结构双向和多维地震动响应.同时，摩擦摆支座性能的有限元计算也在不断发展，通常将其简化为弹簧阻尼单元.2010年，薛素铎等^[16]利用有限元软件SAP2000对应用摩擦摆支座的双层球面网壳结构进行抗震性能分析，但这种简化很难准确描述上部结构和摩擦摆支座之间的相互作用.

本文将摩擦摆支座进行精细化建模，并应用LS-DYNA软件对应用摩擦摆支座的单层球面网壳结构进行有限元分析，讨论三维地震作用下地震动强度及摩擦摆支座参数(摩擦系数和曲率半径)对网壳结构抗震性能的影响规律.

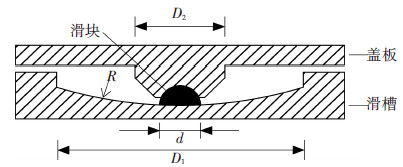
摩擦摆支座由球面滑槽、滑块以及连接上部结构的盖板组成，见图 1，滑块是连接盖板和滑槽的构件，R为球面曲率半径.根据图示，应用摩擦摆支座结构的减震机理可从两个方面进行分析，一方面是当地震动作用在滑槽上时，滑块在滑槽内滑动隔离一部分地震能量，另一方面是滑块在滑槽内滑动时，滑块与滑槽之间相互摩擦消耗一部分能量.

图1(Figure 1)

图1 摩擦摆支座示意

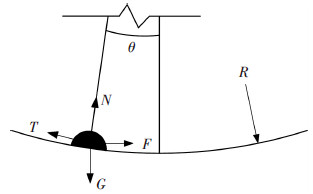
首先，从受力的角度分析结构的减震机理，图 2是滑块受力图，G是上部结构的重力，N是滑槽支反力，T是滑块与滑槽之间的滑动摩擦力，F是滑槽受到的水平剪力，根据平衡条件可得F的表达式为

图2(Figure 2)

图2 滑块受力图

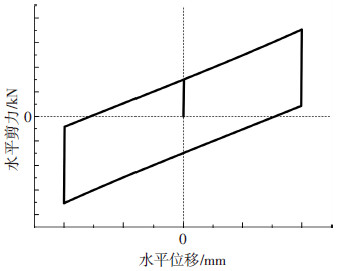
另一方面，从耗能角度分析摩擦摆支座结构的减震机理.摩擦摆支座的滞回曲线见图 3^[1]，结构在水平力或地震作用下，滑块在滑槽内滑动，摩擦摆支座的摩擦耗能大小等于滞回曲线所包裹面积.

图3(Figure 3)

图3 FPB滞回曲线

假设滑块在滑槽中滑动时，滑槽的形状不发生变化，可以将滑槽简化为一个刚性滑面，在有限元建模时，盖板与滑块采用SOLID164单元建模，刚性滑面采用SHELL166单元建模，材料的弹性模量为2.06×10⁵ MPa，材料泊松比为0.3.

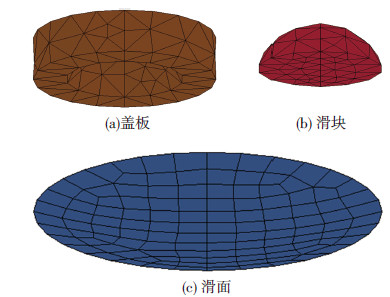
图 1中摩擦摆支座具体尺寸，D₁、D₂和d的值分别取70、30和20 cm，经验证尺寸满足要求(滑槽为刚性面，分析摩擦摆支座滑块，静力时最大应力在140 MPa左右，动力时(PGA为400 gal)最大应力在190 MPa左右)，盖板、滑块和滑面单元尺寸越小，计算结果越精确，但计算时间越长，当盖板和滑块单元尺寸小于4 cm，滑面单元最大尺寸小于6 cm时，单元大小的变化对结构响应影响较小，因此取上述尺寸进行网格划分，摩擦摆支座有限元模型见图 4；盖板与滑块以及滑块与刚性面之间通过接触连接(在LS-DYNA软件中采用自动的点面接触，除摩擦系数外，其余参数采用默认值)，上部结构与盖板顶面多个节点耦合连接(防止盖板转动).

图4(Figure 4)

图4 摩擦摆支座有限元模型

选用K8型单层球面网壳作为研究对象，网壳结构参数见表 1.

表1(Table 1)

表1 网壳几何参数 模型 矢跨比 跨度/m 斜杆 环杆和肋杆 最外环杆 模型一 1/5 80 Φ159×6 Φ180×8 Φ180×8 模型二 1/5 80 Φ159×6 Φ180×8 Φ299×10 模型三 1/5 80 Φ159×6 Φ180×8 Φ299×20

表1 网壳几何参数

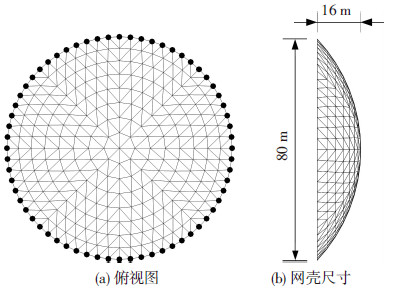
计算分析时采用弹性假设，在LS-DYNA有限元软件中，网壳结构杆件选用空间梁单元(BEAM161)进行模拟，节点定义为刚接，屋面荷载为1 kN/m²，用质量单元(MASS166)模拟，材料的弹性模量为2.06×10⁵ MPa，泊松比为0.3，结构的阻尼比为0.02.选用固定铰支座和实体摩擦摆支座，两种支座均安装在最外环节点的下部，网壳平面图和支座布置见图 5，图中•表示摩擦摆支座安装位置.

图5(Figure 5)

图5 摩擦摆支座布置

网壳结构选用表 1中的模型，以曲率半径为1 m，摩擦系数为0.1的摩擦摆支座为例，分析结构静力作用下的内力和变形，并与铰支座结构所得结果进行对比，见表 2.应用摩擦摆支座的结构变形和内力明显增加，这是因为将铰支座改为摩擦摆支座以后，结构的水平支承明显减弱，因此，结构的变形增加；应用摩擦摆支座结构最外环杆件起约束结构水平变形的作用，因此，最外环杆件内力增加(增加100多倍)，而其余杆件的作用没有发生较大变化，所以应力变化较小；加强最外环杆件能有效地减小结构的变形，从7.50 cm减小到2.86 cm，除最外环杆件外，其余杆件应力变化较小，如，肋杆、环杆和斜杆的应力分别在35、36和43 MPa左右；由于截面积增加，外环杆件应力也明显降低.

表2(Table 2)

表2 结构静力力学性能 模型 最大位移/cm 肋杆应力/MPa 环杆应力/MPa 斜杆应力/MPa 最外环杆应力/MPa 模型二(铰接) 1.29 -34.3 -36.3 -38.2 1.35 模型一(FPB) 7.50 -35.9 -36.4 -45.2 264.20 模型二(FPB) 4.16 -35.5 -36.4 -43.1 131.30 模型三(FPB) 2.86 -35.7 -36.4 -42.1 64.30

表2 结构静力力学性能

结构应用摩擦摆支座后，结构受到的水平支承力由滑块与滑槽之间的静摩擦力提供，与铰支座结构相比，支座的水平支撑作用明显减弱，摩擦摆支座对结构承载能力产生不利影响.

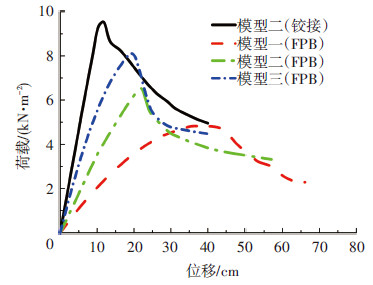
对表 1中3种摩擦摆支座单层网壳结构进行稳定性分析，并与铰支座结构对比，见图 6.应用摩擦摆支座网壳结构的承载力明显小于铰支座结构，而且结构的整体刚度也明显减弱,但随着外环杆件的加强(模型一到模型三最外环杆件逐渐增强)，应用摩擦摆支座的结构承载力增加，并且结构的整体刚度增强.因此，应用摩擦摆支座结构的承载能力明显降低，但加强外环杆件有利于提高结构的承载能力.

图6(Figure 6)

图6 网壳结构荷载位移曲线

静载下，摩擦摆支座不仅使网壳结构的内力和变形增加，而且还使结构承载能力降低；加强结构的外环杆件不仅能够有效减小结构的变形^[17]，而且能明显提高结构承载能力.因此，尽管应用摩擦摆支座减弱了网壳结构的静力性能，但通过加强外环杆件，结构的静力性能能够得到有效改善.

选用K8型单层球面网壳结构作为研究对象，以表 1中模型二为例，摩擦摆支座参数、加载方案以及地震波的选取见表 3，对三维地震动作用下网壳结构的抗震性能进行研究.

表3(Table 3)

表3 FPB参数及加载方案 方案 摩擦系数 曲率半径/m 地震波 地震强度/(cm·s-2) 一 0.025~0.25 1 El-Centro; Taft 70~400 二 0.1 0.5~2.5

表3 FPB参数及加载方案

以曲率半径为1 m，摩擦系数为0.1的摩擦摆支座作为隔震装置，对两种支座形式(铰支座和摩擦摆支座)网壳结构施加El-Centro波，地震动强度为400 cm/s².网壳结构部分地震响应结果见表 4(相对位移是指结构中节点相对最外环节点的位移).

表4(Table 4)

表4 网壳结构地震响应 对比指标 铰支座 FPB 减小量/% 水平 竖向 水平 竖向 水平 竖向 顶点最大位移/cm 18.7 13.8 16.7 11.5 10.7 22.5 顶点最大加速度/(m·s-2) 12.6 39.8 3.0 3.1 76.2 92.2 节点最大相对位移/cm 2.5 8.2 1.1 1.7 56.0 79.3 节点最大加速度/(m·s-2) 13.2 39.8 7.1 5.6 46.2 85.9 肋杆最大应力/MPa -93.7 -47.7 49.1 环杆最大应力/MPa -177.6 -63.5 64.2 斜杆最大应力/MPa -172.4 -69.1 59.9 最外环杆件最大应力/MPa 7.4 148.4 —

表4 网壳结构地震响应

分析表 4可得，与铰支座结构相比，应用摩擦摆支座网壳结构的动力响应明显减弱，如，顶点竖向加速度从39.8 m/s²减小到3.1 m/s²，减小了92.2%，而且杆件(除最外环杆件)的应力均能减小40%以上.

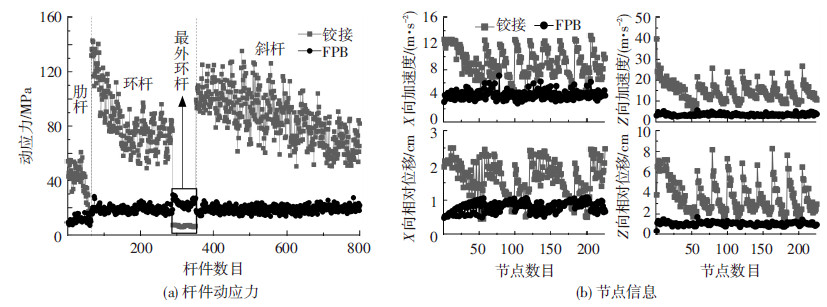
为进一步说明摩擦摆支座隔震效果，对结构所有杆件和节点的动力信息进行对比，见图 7.分析图 7(a)可得，除最外环杆件外，铰支座结构杆件动应力的范围为(0，150)MPa，而应用摩擦摆支座结构杆件的动应力都小于40 MPa，杆件的动应力明显减小，说明摩擦摆支座的隔震效果明显；分析结构节点信息，如图 7(b)所示，可以得到相同结论.

图7(Figure 7)

图7 网壳结构动力力学性能对比

由于结构中杆件和节点数目较多，很难对其一一对比分析，为了方便比较，定义3个评价指标，分别为ρ_s、ρ_d和ρ_a(所有杆件中最大动应力增大系数、所有节点中最大相对位移增大系数和最大加速度增大系数)，具体表达式为：

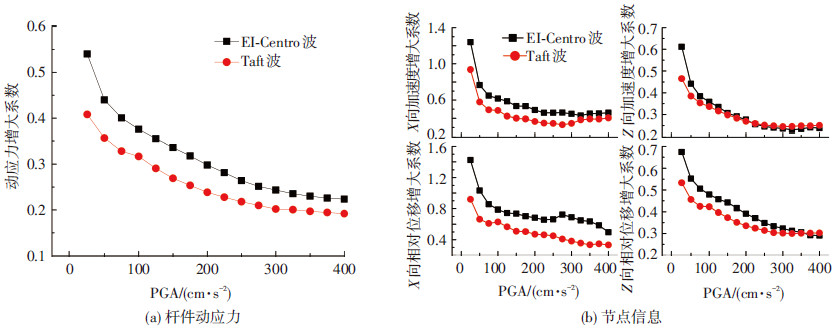
选取曲率半径为1 m、摩擦系数为0.1的摩擦摆支座作为隔震设备，得到增大系数随PGA变化的曲线见图 8.由图 8(a)可得，随着地震动强度的增加，增大系数的值逐渐减小，说明杆件动应力的减小幅度越大，当地震动强度达到400 cm/s²时，动应力能减小75%以上(增大系数小于0.25).为了更全面地分析网壳结构的抗震性能，从水平和竖向两个方面对结构节点位移和加速度增大系数的变化规律进行分析，如图 8(b)所示，当地震动强度大于50 cm/s²时，各增大系数的值都小于1，且随着地震动强度的增加，其值逐渐减小，说明摩擦摆支座的隔震效果越好；由图还可以看出，地震动强度较小时(El-Centro波，PGA＜50 cm/s²)，X向加速度和相对位移的增大系数大于1，这是因为地震动强度较小时，摩擦摆支座的滑块与滑槽之间仍处在粘滞状态，且结构的水平支承较弱，从而使得应用摩擦摆支座网壳结构的变形微弱增加，但变形仍然较小，因此，这种增加可忽略；随着地震动强度的增强，滑块在滑槽上滑动，从而使传递给结构的地震能量减少，所以增大系数逐渐减小.总之，随着地震动强度的增加，应用摩擦摆支座网壳结构抗震性能逐渐增强.

图8(Figure 8)

图8 地震动强度的影响

为保证摩擦摆支座的滑块和滑槽之间良好的滑移性能，在支座的滑道内衬聚四氟乙烯材料，聚四氟乙烯具有耐高温的特点，其摩擦系数极低，根据不同的抛光层度，可以使摩擦系数在不同区间内变化，此种支座的耐久性和可靠性已得到理论和实验验证^{[18, 19]}.滑动速度和压力大小等因素影响此种材料摩擦系数的大小，但影响较小^[20]，因此，本文假设摩擦系数在滑动过程中保持常数.

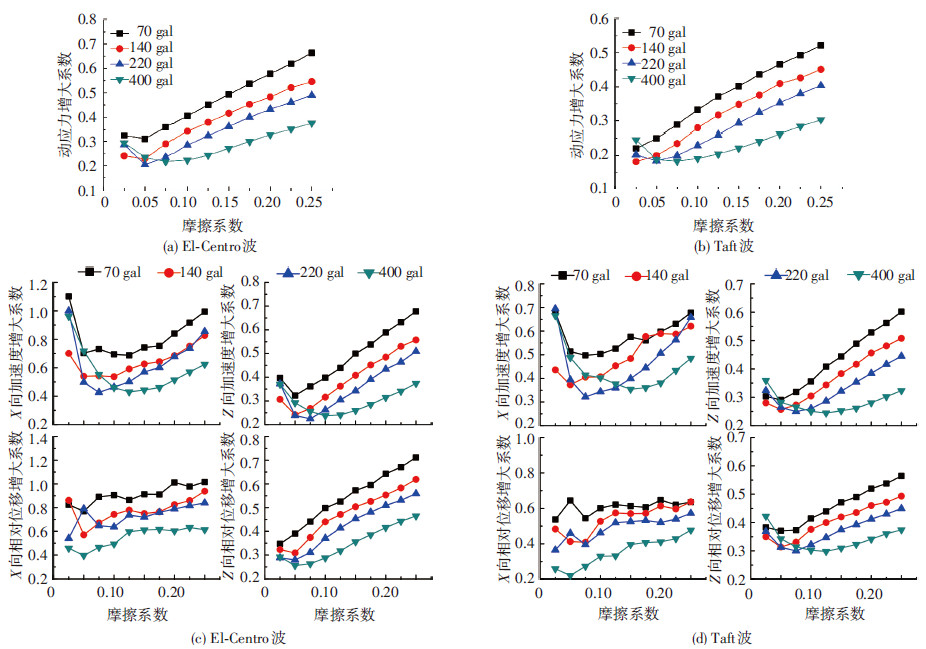
选取表 3中方案一研究摩擦系数对摩擦摆支座隔震性能的影响，得到结构评价指标变化曲线见图 9.随着摩擦系数的增加，多数增大系数的值先减小后增加，说明并非摩擦系数越小隔震效果越好，例如，当摩擦系数小于0.05时，由于摩擦系数较小，使得滑块与滑槽之间的相对位移增加，体现在图 2中就代表角度θ增加，根据式(1)得出水平剪力F增加，上部结构的响应也随之增加，因此，摩擦系数较小时，各种评价指标的值反而较大.

图9(Figure 9)

图9 摩擦系数影响规律

由图 9还可看出，除X向相对位移增大系数变化曲线外，其余曲线的最低点(增大系数最小值所对应的点)随地震动强度的增大而逐渐右移，说明最优摩擦系数(最低点对应的摩擦系数值)随地震动强度的增加而增加；X向相对位移增大系数变化幅度较小，因此，摩擦系数的变化对其影响较小.分析图 9还可得出，曲线的最低点多数落在区间(0.05,0.15)上，即，4种不同地震动强度所对应的最优摩擦系数都在此区间上，与文献[21]给出的区间相同.因此，摩擦系数在区间(0.05,0.15)上取值时，支座的隔震效果较好.

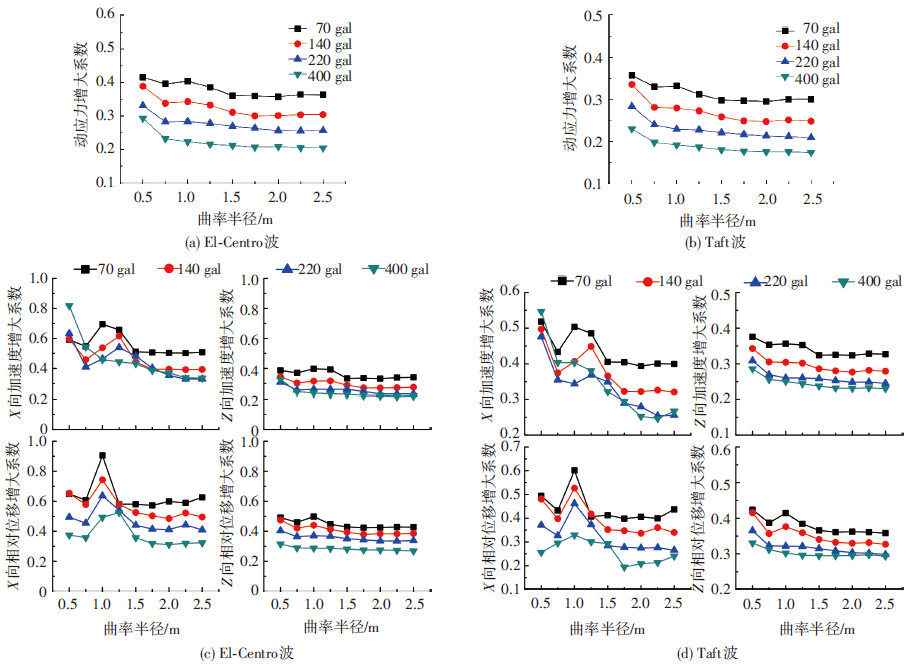
选取表 3中方案二研究曲率半径的影响，得到结构的评价指标变化曲线见图 10.图中多数曲线都是逐渐下降的(增大系数逐渐减小)，由此说明，摩擦摆支座曲率半径越大，隔震效果越好，这与文献[10, 16]所得结论相近；当曲率半径大于2.0 m时，几乎所有曲线都接近水平，说明此时曲率半径的变化对网壳结构抗震性能的影响较小，因此，可以选择曲率半径大于2.0 m的摩擦摆支座作为网壳结构的隔震设备.此外，根据图 1、2可得出，当滑块和滑槽之间相对位移一定时，曲率半径R越小，旋转角度θ就越大，再根据式(1)，角度θ越大，恢复力F越大，因此，为了保证摩擦摆支座有良好的自恢复性能，摩擦摆支座曲率半径越小越好.由图 10还可看出，当选用曲率半径为1 m的摩擦摆支座作为隔震支座时，各增大系数的值较大，这是因为网壳结构的自振周期和摩擦摆支座的周期相近，分别为1.87和1.98 s，因此，不应选择周期与结构自振周期相近的摩擦摆支座作为隔震设备.

图10(Figure 10)

图10 曲率半径影响规律

综上所述，当摩擦摆支座所用材料的摩擦系数为0.1时，选择曲率半径为2.0 m的摩擦摆支座作为隔震装置可以使网壳结构的抗震性能最好.文献[10, 16]给出摩擦摆支座的曲率半径应该大于1 m，因此，曲率半径为2.0 m的摩擦摆支座满足这个要求.

1)静载下，应用摩擦摆支座网壳结构不仅内力和变形增加，而且承载能力也明显降低，但通过加强结构的外环杆件可有效减弱此种不利影响.

2)随着地震动强度的增加，摩擦摆支座的隔震效果增强，即，应用摩擦摆支座的网壳结构抗震性能增强.

3)随着地震动强度的增加，摩擦摆支座的最优摩擦系数取值也随之增加；对于给定曲率半径的摩擦摆支座，存在一个最优区间，当摩擦系数在此区间上取值时，结构的抗震性能较好.

4)摩擦摆支座的曲率半径越大隔震效果越好，但曲率半径越小，摩擦摆支座自恢复能力越强，因此，建议在保证良好恢复力的前提下，选取曲率半径较大的摩擦摆支座作为隔震设备.