2002年，瑞士Airlight Ltd.总工程师Pedretti^[1]提出一种新型结构体系——气撑式张弦结构(Tensairity)，该结构是在张拉整体式结构(Tensegrity)基础上加入第三种稳定元素空气而来，这不但继承了张拉整体式结构的良好受力性能和较高的材料利用率，更因为加入了气囊，而使得其具有更强的建筑表现力和视觉冲击力^[2].

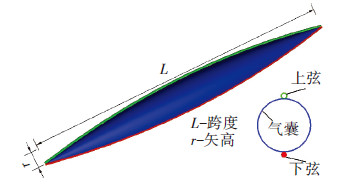
气撑式张弦结构由上弦刚性杆，下弦柔性拉索和中间低压充气气囊组成(图 1)，可看成由传统张弦结构中的撑杆被低压充气气囊取代得到.该结构利用气囊内压建立初始预应力，实现了拉压分离，并且避免了撑杆的稳定性问题，使材料得到了充分利用.

图1(Figure 1)

图1 气撑式张弦结构示意

国际上主要有瑞士的Airlight Ltd.和EMPA组合结构研究中心开展气撑式张弦结构的研究工作^{[3, 4, 5]}.气撑式张弦结构已在实际工程中得到应用(图 2).这是一种典型的刚柔混合结构，与传统张弦梁类似，在预应力作用下会发生位形变化，需要进行找形分析，得到结构的零状态放样几何，并且找形分析对结构的力学性能影响亦是大家关心的.

图2(Figure 2)

图2 气撑式张弦结构工程应用实例

气撑式张弦结构的受力状态与传统张弦梁结构基本一致，可以分为零状态、初始态和荷载态3部分^[6].零状态，即结构体系在无自重、无预应力和外荷载作用下的放样状态，此时各构件的应力为零，之所以在零状态不考虑结构自重，是因为气撑式张弦结构在施工过程中，各个构件是由工厂预制，在地面拼装完成后吊装的; 初始态，即结构体系在自重和预应力作用下的平衡状态，初始态对应的几何参数一般即指设计图纸上的几何外形，此时对于气撑式张弦结构来说，气囊内压和下弦预应力已经施加完毕，并且吊装就位，故在此阶段应该考虑结构自重; 荷载态，即结构体系在自重、预应力和外荷载共同作用下的受力状态，此时结构整体施工完毕，气撑式张弦结构进入正常工作状态.

采用Beam188单元模拟上弦刚性的压弯构件，采用Shell181单元来模拟低压气囊，采用Link10单元来模拟下弦柔性索.为了能有效建立结构整体的预应力，还必须考虑索-膜之间的相对滑移，故在索和膜接触点之间设置接触单元Conta178，可设置该单元的摩擦系数为0，这样做带来的误差不会超过5%^[7].

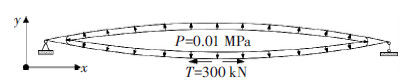
纺锤形气撑式张弦梁各个构件的参数见表 1.纺锤形气撑式张弦梁按两端简支设置(图 3)，为防止发生平面外扭转，将上弦在平面外进行约束.气囊内压为0.01 MPa，下弦索预应力约为300 kN.

表1(Table 1)

表1 纺锤形气撑式张弦梁构件参数 构件名称 截面尺寸/mm 材料模型 弹性模量/GPa 泊松比 密度/(kg·m-3) 屈服强度/MPa 上弦 Φ400×20 双线性随动强化模型 210 0.3 7 800 235 下弦 Φ60 双线性随动强化模型 195 0.3 7 800 1 860 气囊 t=1.5 双线性等向强化模型 5 0.2 1 000 100

表1 纺锤形气撑式张弦梁构件参数

图3(Figure 3)

图3 纺锤形气撑式张弦梁模型

目前应用在传统张弦梁结构找形分析上的方法主要包括：逆迭代法^[8]、改进的逆迭代法^[9]、分级卸载法^[10].前两种方法的算法本质相同，区别在于改进的逆迭代法采用降温法施加预应力，而逆迭代法是通过断开端部索段，直接施加拉力实现的.分级卸载法的力学本质是将初始态上弦内力逐步卸载为零，从而得到上弦的零态位形.改进的逆迭代法相对其他两种方法的优点是：不破坏结构完整性，可在找形后结构上考察结构荷载态性能；此外，该方法更加直观，无需取隔离体，可结合通用有限元程序提供的脚本语言实现，所以改进的逆迭代方法更适合气撑式张弦梁结构的找形分析，具体迭代步骤：

假定图纸给定的结构初始态坐标为U₀={X Y Z}₀，经过第k次迭代后所得的零状态几何坐标为U_k={X Y Z}_k，对应的初始态坐标为U_0k={X Y Z}_0k.

1)假设当前的初始态几何即为零状态几何，即令U₁={X Y Z}₁={X Y Z}₀，k=1；

2)对气囊施加内压，在索段施加温度预应力，对结构施加自重，对几何为U_k的结构计算位移，得到对应初始态坐标U_0k；

3)计算经k次迭代后的位形误差D_k，即令D_k=U_0k－U₀；

4)判别D_k是否满足给定的精度.若满足，则U_k即为所求的零状态几何坐标，若不满足，则令U_k+1=U_k－βD_k(β为迭代控制系数，0＜β＜1，减小修正幅度，有利于模型计算的收敛性)，转步骤2)，并令k=k+1；

5)由以上步骤计算出零状态的几何参数后，将初应变值赋予该索段求出平衡后所得到的状态即为初始态预应力分布.此时,应当检验该索段的内力值是否为预定值，如果不是，则应当调整索的预应力值从步骤2)重新计算.

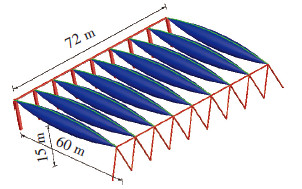
图 4为一临时建筑，上部采用气撑式张弦梁结构，一端铰接于固定柱，另一端铰接于人字形摇摆柱.结构整体高度15 m，跨度60 m，相邻两榀气撑式张弦梁间距为9 m，共9榀.建筑地点为某临海区域.现取中部一榀进行找形分析，确定结构的零态几何.

图4(Figure 4)

图4 临时建筑

使用通用有限元软件ANSYS提供的APDL语言，编写改进的逆迭代几何找形方法，以上弦的跨中节点作为控制点，取β=0.5，经计算得到各迭代步的精度见表 2(D_k代表控制点精度).

表2(Table 2)

表2 各迭代步精度 迭代次数k Dk /m (Dk/r )/% 1 0.659 7 21.99 2 0.288 1 9.60 3 0.121 9 4.06 4 0.094 4 3.15 5 0.040 9 1.36 6 0.032 5 1.08 7 0.014 2 0.47 8 0.011 4 0.38 9 0.005 0 0.17 10 0.004 0 0.13 11 0.001 8 0.06 12 0.001 4 0.05 13 0.000 6 0.02

表2 各迭代步精度

观察表 2，可发现经过13次迭代，得到控制点的绝对误差为0.6 mm，相对于矢高的误差为0.02%，满足建筑外观要求，可见改进的逆迭代法可有效解决纺锤形气撑式张弦梁的零态找形问题，但是可发现该方法的收敛速度逐渐降低，这是改进的逆迭代法的缺点之一.

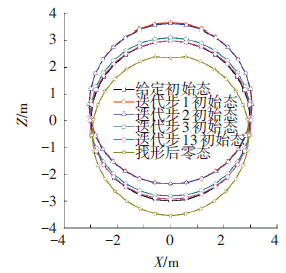
将各迭代步的气囊跨中截面绘制于图 5.可发现，气囊截面在零态时，已经不是标准圆，截面整体有一个明显的向下位移，而且在上弦的位置稍微向内凹陷.这是因为施加预应力后，上弦会产生较大的向上位移，在逆迭代过程中，为了弥补预应力引起的上弦位移，零态时需要在上弦处修正的位形相对其他位置要大，故而气囊跨中截面在上弦的位置会产生向内的凹陷.

图5(Figure 5)

图5 各迭代步跨中气囊断面图

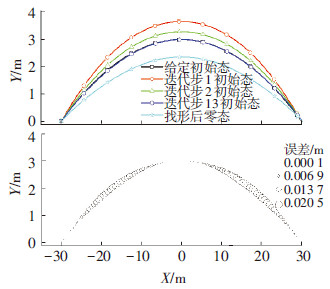
取初始态上弦第1、2、13次迭代后的位形和第13次迭代完成后的上弦零态位形绘制成图 6，可看出，零状态上弦各点Y坐标要低于初始态上弦各点值，而且在可滑动端的X坐标要比未经找形大.取第13次迭代后上弦各点的误差绘制成图 6气泡图，气泡的大小代表绝对误差的大小，误差最大值为20 mm，为矢高的0.67%，满足建筑精度要求.

图6(Figure 6)

图6 上弦找形位形及各点误差

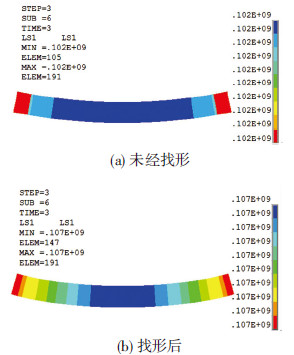
在初始态下，下弦预应力由未经找形288.4 kN，提升到299.7 kN(图 7)，这是因为从零状态到初始态的过程中，上弦跨中向上的位移为0.64 m，要比未经找形的0.66 m小0.02 m，且滑动支座处比未经找形要少向内侧移动0.19 m，由于初始施加的预应力相同，在上述因素共同作用下，找形后下弦预应力的损失要比未经找形少，结果导致找形后的下弦预应力比未经找形要大.对于这种刚柔混合的张弦结构来说，下弦的预应力水平会直接影响到结构承载力，而且在风吸荷载作用下，下弦索是否退出工作将直接取决于下弦索的应力水平.

图7(Figure 7)

图7 初始态下弦索应力(Pa)

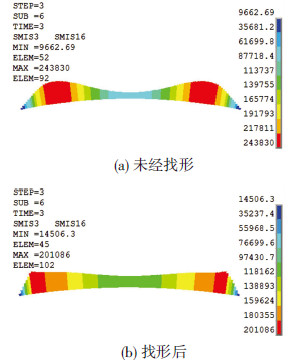
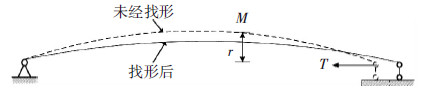
上弦最大负弯矩由未经找形的243.8 kN·m降低到205.1 kN·m，但是弯矩的分布更加均匀(图 8).可认为上弦任意一点弯矩M只跟支座处下弦的水平拉力T，所求弯矩点处上弦挠度r，以及支座到所求点之间的均布气囊支撑力q有关(图 9)，可近似表示为

图8(Figure 8)

图8 初始态上弦弯矩(N·m)

图9(Figure 9)

图9 未经找形与找形后初始态上弦受力简图

M=f(T,r,q)，

对该式求全微分可得

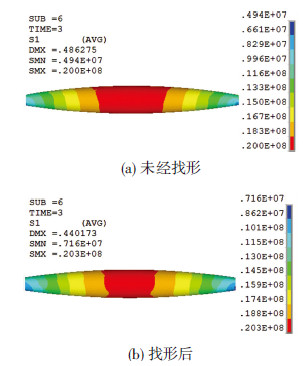
从图 10可看出，气囊的第一主应力前后变化不大，最大值都出现在跨中，数值分别为20.0和20.3 MPa，理论值为${\sigma _{r1}} = q\frac{R}{t} = 0.01 \times \frac{3}{{0.0015}}$=20 MPa，可见模拟结果与理论值吻合较好.

图10(Figure 10)

图10 初始态气囊第一主应力(Pa)

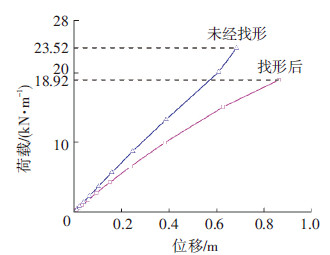
采用弧长法分别对未经找形与找形后的纺锤形气撑式张弦梁进行极限承载力计算，见图 11.找形后的结构在竖向均布荷载作用下的极限承载力为18.29 kN/m，要比未经找形的23.52 kN/m低22.24%，说明找形后承载力的降低不可忽视.

图11(Figure 11)

图11 未经找形与找形后结构荷载位移曲线

未经找形与找形后结构达到极限承载力时的破坏模式相同，见图 12，上弦距支座约1/5处全截面进入塑性，引起结构破坏.说明充气气囊的刚度不足，容易使结构局部变形过大，形成应力集中，最终导致结构局部进入塑性而发生破坏.

图12(Figure 12)

图12 极限状态结构上弦弯矩(N·m)

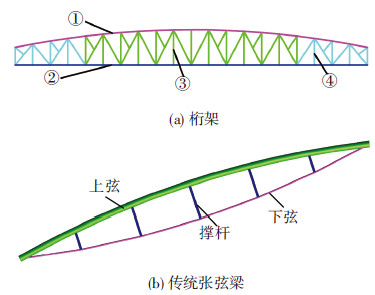
根据文献[11]，以找形后纺锤形气撑式张弦梁结构的极限承载力为设计基准，分别设计相同跨度的桁架结构和传统张弦结构.桁架结构上弦的每个节点都布置了平面外支撑，计算时不考虑平面外稳定问题.桁架的设计简图见图 13(a)，桁架使用的材料列于表 3(钢材型号为Q235).

表3(Table 3)

表3 桁架材料表 杆件编号 截面尺寸/mm 用钢量/(kg·m-2) ① 2∟180×110×14 22.44 ② 2∟110×12 ③ 2∟110×70×7 ④ 2∟125×80×12

表3 桁架材料表

传统张弦梁的设计见图 13(b)，采用与气撑式张弦结构具有相同截面的上下弦，为了在对比经济性的同时，分析气撑式张弦梁与传统张弦梁的刚度差异.使用的材料列于表 4.

图13(Figure 13)

图13 桁架和传统张弦梁结构设计简图

表4(Table 4)

表4 传统张弦梁材料表 构件名称 截面尺寸/mm 用钢量/(kg·m-2) 上弦 Φ400×20 25.93 下弦 Φ60 撑杆 Φ219×12

表4 传统张弦梁材料表

参考规范^[12]，取恒荷载控制下的荷载组合值q=12.38 kN/m为计算工况，将上述3种结构(气撑式张弦梁和传统张弦梁均经过找形分析)在该工况作用下的用钢量、跨中位移、上弦弯矩、下弦应力和上弦应力等项目进行对比，列于表 5.

表5(Table 5)

表5 3种结构对比表 对比项目 用钢量/(kg·m-2) 跨中竖向位移/m 上弦弯矩/(kN·m) 下弦应力/MPa 上弦应力/MPa 桁架 22.44 -0.122 — 183 -170 传统张弦梁 25.93 -0.222 194.84 400 -85.50 气撑式张弦梁 14.63+2.07(膜) -0.492 164.17 469 -70.55

表5 3种结构对比表

1)利用改进的逆迭代法进行找形分析后，初始态上弦与设计给定位形最大相对误差只有0.67%，可将初始位移控制在建筑误差允许范围内，并且可准确给出各构件零状态的放样几何.

2)找形后初始态结构上弦最大负弯矩减小，并且弯矩分布较未经找形时要均匀，这使得结构的初始拱效应降低，计算结果表明，在本文给出的例题中结构承载力降低了22.24%.对于结构设计来说，这是不容忽视的.因此，在对气撑式张弦结构进行荷载态分析前，先进行找形分析是必要的.

3)对大跨度结构来说，气撑式张弦结构的用钢量只有传统张弦梁的65.20%，具有质量轻，施工便捷等优点，具有较高的经济性.

4)相对于桁架结构和传统张弦结构，气撑式张弦结构的刚度较低，对荷载更敏感，设计过程中应适当提高结构的安全度.