2. 陕西省建筑科学研究院, 710082 西安
2. Shaanxi Research Institute of Building Sciences,710082 Xi’an,China
一般地,纯摩擦滑移隔震结构可获得较好的隔震效果,但在大震作用下上部结构会产生过大的位移,从而造成管道排线等建筑物附属设备的损坏,影响建筑物的使用功能,因此滑移隔震支座应配合限位装置一起使用.而限位装置预留滑移量的大小对结构的隔震效果有一定的影响,因此有必要对不同预留滑移量下隔震结构的地震反应进行研究.目前,对滑移隔震结构的地震反应分析通常采用SAP2000、ANSYS、ABAQUS等大型商业有限元分析软件.熊仲明等[1]运用SAP2000软件对一固定滑移量的隔震结构进行了动力分析,认为预留滑移量可以克服无预留滑移量限位装置一滑就限增加隔震结构地震反应的缺陷;王社良等[2]利用ABAQUS软件,探讨了一框架结构模型在不同ELCentro波峰值加速度时的动力反应规律;杨佳玲等[3]采用ANSYS对不同地震烈度、不同场地条件下的滑移隔震结构进行了动力反应分析.但是这些软件往往不能灵活解决科研中遇到的具有个性化的问题,如求解参数的最优值问题需要改变参数做大量重复计算.
Simulink是MATLAB中的一种可视化仿真工具,它提供了一个建立模型方块图的图形用户接口(GUI),只需进行鼠标的简单拖拉操作便可构造出结构的仿真模型[4].但是,由于Simulink建模采用了计算机、通信和控制等专业的分层结构,需要MATLAB程序和GUI工具配合使用,Simulink在土木工程结构分析中的应用还很少[5].作者以软钢实体棒为限位消能装置,运用Stateflow逻辑框图[6]来模拟隔震层的运动状态,采用Bouc-Wen模型来描述弹塑性杆件限位器的滞回特性,建立了滑移隔震结构的Simulink仿真模型,将纯摩擦的动力反应与振动台试验结果进行对比,验证了Simulink仿真技术的可靠性,并探讨了不同预留滑移量下隔震结构的动力反应和能量反应规律.
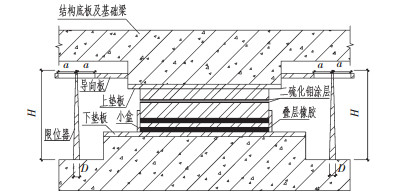
1 滑移隔震支座 1.1 隔震支座构造设计二硫化钼是一种无机盐,具有良好的抗高压、耐高温、低摩擦和速度适应范围宽等优点[7],这里采用二硫化钼作为滑移材料,设计和制作了一种新型滑移隔震装置,见图 1.上下钢垫板分别通过预埋螺栓与混凝土结构连接.二硫化钼涂层应有一定的厚度,以避免滑动摩擦过程中涂层的破坏,使摩擦滑移隔震失效;在下摩擦板中加入叠层橡胶垫可以使隔震层各支座之间受力均匀,防止振动工程中可能引起的结构扭转;小盒防止了下摩擦板中的叠层橡胶与钢板之间受拉破裂;预埋导向板上留有边长为2a的正方形孔槽,以避免X向导向板在Y向地震中受扭破坏;圆锥钢棒限位器底端直径为D,高为H,沿着导向板滑移,预留滑移量为a.当结构受到地震激励时,摩擦面开始相对滑动,当滑移距离达到a时,限位消能器开始工作,摩擦滑移作用可以削弱地震能量向上部结构的传递,限位消能器可以耗散地震能量同时限制上部结构产生过大滑动位移,从而实现隔震支座的滑移限位功能.
|
图1 滑移隔震支座示意 |
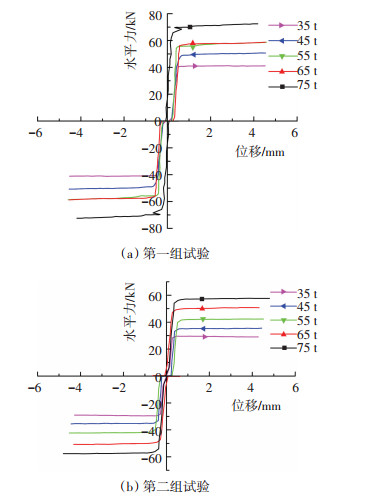
采用MTS电液伺服试验系统对滑移隔震支座的摩擦性能进行测试,试验装置见图 2.试验中共制作两组试件,第二组的试件仅仅更换了中间滑块.竖向荷载分别为35、45、55、65、75 t,每种工况重复加载一次.图 3给出了第二次加载时两组试件的水平力-位移曲线,可以看出滑移隔震支座的摩擦性能稳定,摩擦恢复力曲线符合库伦摩擦力模型.根据库仑定律计算出隔震支座的摩擦系数,约为0.04~0.05.

|
图2 MTS加载试验装置 |
|
图3 第二次加载时的水平力-位移曲线 |
将摩擦滑移隔震结构分为上部结构和隔震层两部分,可分别列出其各自的运动方程.考虑限位器的作用,隔震层的运动方程为
| $ - {m_0}\left( {{{\ddot x}_0} + {{\ddot x}_g}} \right) + {f_d} + {f_u} + F = 0. $ | (1) |
式中:m0为隔震层质量; ${\ddot x_0} + {\ddot x_g} $为隔震层的绝对加速度值;fu为限位器对隔震层的恢复力;fd为库伦摩擦力,$ {f_d} = - {\mathop{\rm sgn}} \left( {{{\dot x}_0}} \right)\mu \sum\nolimits_0^n {{m_i}g} $;F为上部结构对隔震层的反馈作用力,$ F = {c_1}{{\dot x}_1} + {k_1}{x_1},\dot x{x_1}$为结构一层相对于隔震层的速度和位移.
将隔震层的绝对加速度视为上部结构的地震激励,当受到一维地震激励时,上部结构相对于隔震层的运动方程可表示为
| $ \left[ M \right]\left\{ {\ddot x} \right\} + \left[ C \right]\left\{ {\dot x} \right\} + \left[ K \right]\left\{ x \right\} = - \left[ M \right]\left\{ 1 \right\}\left( {{{\ddot x}_0} + {{\ddot x}_g}} \right). $ | (2) |
式中:[M]、[C]、[K]分别为上部结构的质量矩阵、阻尼矩阵和刚度矩阵; $ \left\{ x \right\}$、 $\left\{ {\dot x} \right\} $、$ \left\{ {\ddot x} \right\}$分别为上部结构相对于隔震层的水平位移向量、速度向量、加速度向量;{1}为元素均为1列向量.
引入状态向量 $Z\left( t \right) = {\left[{\begin{array}{*{20}{c}} {X\left( t \right)}\\ {\dot X\left( t \right)} \end{array}} \right]_{2n \times 1}} $,
则上部结构系统的状态空间方程为
| $ \left\{ \begin{array}{l} \dot Z\left( t \right) = AZ\left( t \right) + BU\left( t \right),\\ Y\left( t \right) = CZ\left( t \right) + DU\left( t \right). \end{array} \right. $ | (3) |
式中: $A = {\left[{\begin{array}{*{20}{c}} {{0_{n \times n}}}&{{I_{n \times n}}}\\ { - {M^{ - 1}}K}&{ - {M^{ - 1}}C} \end{array}} \right]_{2n \times 2n}};B = {\left[{\begin{array}{*{20}{c}} {{0_{n \times n}}}\\ {{M^{ - 1}}} \end{array}} \right]_{2n \times 2n}};C = {\left[I \right]_{2n \times 2n}},$,[I]是下角标标注维数的单位矩阵;D=[0]2n×n,[0]是下角标标注维数的零矩阵; $ U\left( t \right) = - \left[M \right]\left\{ 1 \right\}\left( {{{\ddot x}_0} + {{\ddot x}_g}} \right);$;Y(t)为系统输出矩阵.
由状态方程即可求解出上部结构相对于隔震层的位移和速度,由于Simulink中的Derivative导数模块求解器在输入变化比较快时不会使用较小的时间步长,为减小误差,其加速度不宜由速度直接求导得出,可由式(4)直接求出:
| $ \left\{ {\ddot x} \right\} = {\left[ M \right]^{ - 1}}\left\{ { - \left[ M \right]\left\{ 1 \right\}\left( {{{\ddot x}_0} + {{\ddot x}_g}} \right) - \left[ C \right]\left\{ {\dot x} \right\} - \left[ K \right]\left\{ x \right\}} \right\}. $ | (4) |
对于剪切型多自由度串联体系,其层间剪力矢量为
| $ \left[ {{F_s}} \right] = {\left[ {{F_{s1}}\;\;\;{F_{s2}}\;\; \cdots \;\;{F_{sn}}} \right]^T} = - \left[ {{K_{Fs}}} \right]\left[ M \right]\left\{ {\bar x\left( t \right)} \right\}. $ | (5) |
式中:Fs1~Fsn为第1到第n层的层间剪力值;层间剪力增益矩阵 $ \left[{{K_{Fs}}} \right] = \left[{\begin{array}{*{20}{c}} 1&1& \cdots &1\\ {}&1& \cdots &1\\ {}&{}& \ddots &1\\ {}&{}&{}&1 \end{array}} \right]$;上部结构绝对加速度向量 $\left\{ {\bar x\left( t \right)} \right\} = {\left\{ {{{\ddot x}_1} + {{\ddot x}_0} + {{\ddot x}_g},{{\ddot x}_2} + {{\ddot x}_0} + {{\ddot x}_g},\cdots ,{{\ddot x}_n} + {{\ddot x}_0} + {{\ddot x}_g}} \right\}^T},{{\ddot x}_i}\left( {i = 1,2,\cdots ,n} \right) $为结构第i层相对于隔震层的加速度.
反馈于隔震层的作用力Fin为上部结构与m0之间的相互作用,在Simulink仿真中,如果取Fin=Fs1直接求出Fin并反馈于隔震层,则会形成在每时间步迭代的代数环,为避免代数环的产生,可由式(5)间接得到上部结构对隔震层的反馈力Fin:
| $ \begin{array}{l} {F_{in}} = {F_{s1}} = \left[ {1\;\;\;0\;\;\; \cdots \;\;0} \right]\left\{ {{F_s}} \right\} = \\ \;\;\;\;\;\; - \left[ {1\;\;\;1\;\; \cdots \;\;1} \right]\left[ M \right]\left\{ {\bar x\left( t \right)} \right\} = \\ \;\;\;\;\;\left[ {1\;\;\;1\;\; \cdots \;{\rm{1}}} \right]\left\{ {\left[ C \right]\left\{ {\dot x} \right\} + \left[ K \right]\left\{ x \right\}} \right\}. \end{array} $ | (6) |
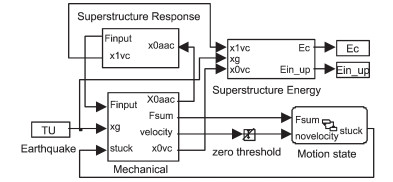
基础滑移隔震结构体系的Simulink仿真主模型见图 4.该模型有四大子系统Supstructure Response(上部结构反应)、Mechanical(隔震层)、Motion State(运动状态判定)和Supstructure Energy(上部结构能量反应).限于篇幅,这里给出几个重要仿真模型的建立.
|
图4 隔震结构体系Simulink仿真主模型 |
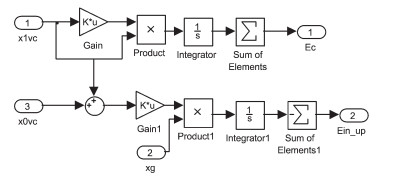
隔震层采用非连续性库伦摩擦力模型,令静摩擦系数和动摩擦系数相等,且值取为0.05,并利用MATLAB/Simulink中的Stateflow模块进行静止与运动状态转换的模拟仿真,则可建立库伦摩擦力Simulink仿真模型[8].滑移隔震体系的变形主要集中于隔震层,上部结构近似为刚体做水平运动,保持弹性状态,因此当地震作用终了时,结构体系的动能和变形能可忽略不计,此时隔震体系的能量反应只有地震总输入能、阻尼耗能和隔震层滞回耗能.根据能量计算公式[9]可得到上部结构的能量仿真模型,见图 5.
|
图5 能量反应Simulink仿真模型 |
Bouc-Wen模型[10, 11]在积分过程中不需对拐点进行反复迭代,有效解决了刚度突变问题,避免了由于刚度突变在计算过程中引起较大误差.软钢实体圆锥棒的滞回特性可采用Bouc-Wen模型来描述,其恢复力由弹性恢复力FE和滞回力FH组成,表达式为
| $ F = {F_E} + {F_H} = r{k_1}x + \left( {1 - r} \right){k_1}z. $ | (7) |
式中:F为限位器对隔震层提供的恢复力;k1为限位器的弹性刚度;r为限位器屈服后刚度k2与弹性刚度k1的比;x为隔震层的相对位移;z为描述滞回特性的变量,变化范围为z≤xy,且当z=xy,表明此时处于屈服阶段.z可表示为
| $ \dot z = \dot x\left[ {A - \left( {\beta + \alpha {\mathop{\rm sgn}} \left( {\dot xz} \right)} \right){{\left| {\frac{z}{{{x_y}}}} \right|}^n}} \right]. $ | (8) |
式中:xy为圆锥棒限位器屈服位移;A、α、β、n为参数,A参数控制着滞回环的幅度,α、β控制着滞回环的一般形状,n控制着滞回曲线的光滑程度,n的值越大,Bouc-Wen模型所表述的曲线越逼近于理想弹塑性模型,n的取值一般大于20.
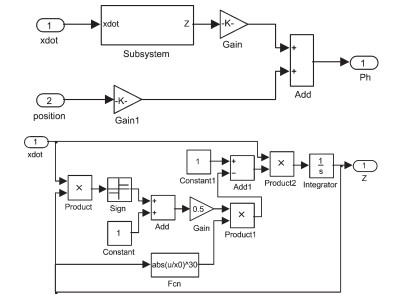
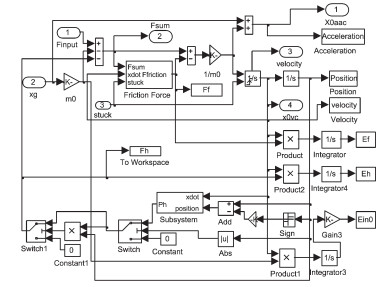
软钢实体圆锥棒恢复力的Simulink仿真模型见图 6,隔震层的仿真模型见图 7.
|
图6 限位消能器Simulink仿真模型 |
|
图7 隔震层仿真模型 |
基于量纲理论,在综合考虑振动台承载能力的基础上,采用欠质量模型设计了一个5层混凝土框架结构模型,其长度相似比和变位相似比均为0.2,加速度相似比为1.97.框架结构平面呈矩形对称布置,柱距1.2 m,首层层高0.84 m,二层到五层层高均为0.72 m,模型总高度为3.72 m,高宽比为1.55.模型首层底板厚0.2 m,基础板厚为0.1 m,可与振动台面连接,隔震支座布置在结构底板和基础板之间,每个柱子的底部布置一个,共9个.二层到五层设置配重块,每层4块,配重块为现浇混凝土块,尺寸为0.8 m×0.8 m×0.3 m.振动台试验模型及隔震支座布置见图 8.数值模拟分析采用其原型结构,仿真时将摩擦系数和预留滑移量调为无穷大,即可得到抗震模型和纯滑移模型的地震反应.

|
图8 试验框架模型及隔震支座布置 |
地震动选取两条强震记录EL Centro波和天津波,峰值加速度分别为341.7 gal和104.18 gal,按8度罕遇地震调幅后为400 gal,沿结构x向单向加载,持时30 s,步长0.02 s.
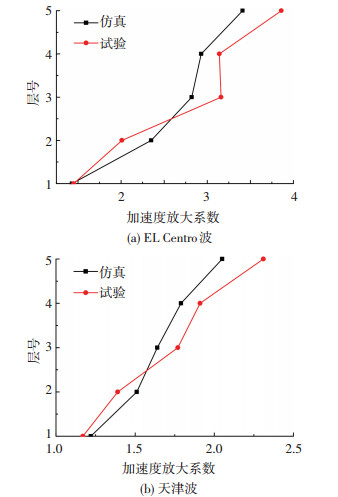
4.3 试验与仿真对比基于试验模型的相似关系,由试验模型的隔震层位移推出结构原型的位移值,并与仿真结果对比,见表 1.由于试验模型的加速度放大系数推出到原型结构,其值不变,为了方便比较,选择抗震结构的加速度放大系数进行对比,见图 9.可看出,由隔震层位移推出的结构原型值与仿真值较为接近,误差较小,加速度反应的试验值和仿真值吻合较好,MATLAB/Simulink仿真技术可对摩擦滑移隔震结构进行强震记录下的地震反应分析.
| 表1 纯滑移结构隔震层位移的仿真与试验值 |
|
图9 抗震结构的加速度放大系数对比曲线 |
隔震层所有圆锥棒限位消能器为同一规格,由普通碳素钢A3钢棒Φ100制成,平均屈服强度为208.8 N/mm2,平均弹性模量为214.07 GPa,底端直径D为100 mm,顶端直径D0为60 mm,高H为400 mm,斜锥度i为0.05,其他参数可根据文献[12]计算求得,具体参数见表 2.仿真分析时,隔震层限位器滞回曲线各参数的取值分别为A=1,α=0.5,β=0.5,n=30.分析时地震动选取EL Centro波,隔震层预留滑移量分别取为0 mm和最大滑移量的20%和40%.最大滑移量为纯摩擦时隔震层的相对位移,在隔震层Simulink模型中将限位消能器的恢复力取为0即可通过仿真得到.
| 表2 隔震层限位器参数 |
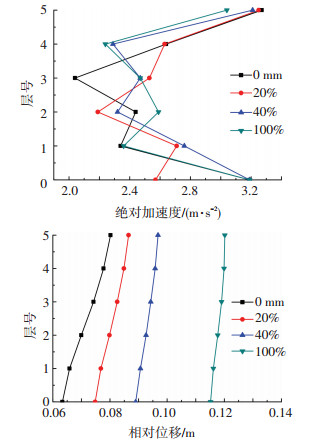
图 10给出不同滑移量下隔震结构的加速度反应和相对位移反应.由于限位消能钢棒的加入改变了结构的整体受力特性,结构的加速度变化变得较为复杂,各层的大小变化规律各异,相比纯滑移结构,限位器工作后并没有明显增加上部结构的加速度反应.随着预留滑移量的增大,相对位移曲线的斜度越大,上部结构越接近平动,隔震层的滑移量逐渐增大,最大滑移量在0 mm限位时为63.34 mm,20%限位时为74.82 mm,40%限位时为88.99mm,纯滑移时为115.20 mm,而限位器的最大变形逐渐减小,分别为63.34、51.82、42.99、0 mm,变形越大,地震过程中越容易弯曲破坏,震后更换的概率越高,从而增加工程成本.因此实际工程应用时,在结构最大滑移量范围内,选择的预留滑移量应尽量使限位器变形较小.
|
图10 不同滑移量下隔震结构的动力反应 |
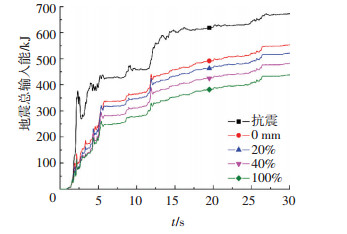
表 3给出了不同预留滑移量下结构体系各部分能量的分配情况,图 11给出了地震总输入能的时程对比图.
| 表3 不同滑移量下结构体系的能量分配 |
|
图11 结构体系的地震总输入能时程 |
地震总输入能随着预留滑移量的增大逐渐减小,隔震性能逐渐提高;抗震时,结构主要靠内部阻尼耗能,而滑移时上部结构的阻尼耗能比几乎不变,为0.13左右,阻尼耗能与预留滑移量关系不大,而主要是与摩擦系数有关;隔震层总滞回耗能随预留滑移量的增大而减小,且以摩擦耗能为主,由于总输入能也逐渐减小,其滞回耗能比也变化不大,在0.86左右,相比抗震结构,不同滑移量下的隔震层都能较好地发挥滞回耗能.
4.4.3 隔震层滞回曲线隔震层的滞回曲线可通过Simulink库中的XY Graph模块直接画出.图 12给出了0 mm预留滑移量下的摩擦恢复力曲线和限位器恢复力曲线.可看出,两者的滞回曲线饱满,能较好地耗散地震能量,且摩擦力曲线符合间断型库伦模型,限位器恢复力曲线符合双线性模型.

|
图12 0 mm滑移量下的摩擦力和限位器恢复力曲线 |
1)抗震结构加速度反应的试验值与仿真值基本吻合,滑移结构隔震层位移的推出值与仿真值较为接近,误差较小,表明MATLAB/Simulink仿真技术可对摩擦滑移隔震结构进行地震反应分析.
2)限位装置的加入改变了结构的整体受力特性,使结构的加速度变化变得较为复杂,相比纯滑移结构,限位器工作时并没有明显增加上部结构的加速度反应.随预留滑移量的增大,隔震层的最大滑移量逐渐增大,而限位器的最大变形不断减小.一般地,限位器变形越大,地震过程中越容易弯曲破坏,震后更换的概率越高,从而增加工程成本.因此实际工程应用时,在结构最大滑移量范围内,选择的预留滑移量应尽量使限位器变形较小.
3)地震总输入能随着预留滑移量的增大逐渐减小,隔震性能不断提高.抗震时结构主要靠内部阻尼耗能;滑移时以摩擦耗能为主,且上部结构的阻尼耗能比和隔震层的总滞回耗能比变化不大,不同滑移量下的减震效果相当,这说明阻尼耗能与预留滑移量关系不大,滑移量的变化主要改变了隔震结构体系的地震输入能量,而对其他能量指标影响较小.
4)隔震层的滞回曲线饱满,能够较好地耗散地震能量,且摩擦力曲线符合间断型库伦模型,限位器恢复力曲线符合双线性模型,表明文中对摩擦力模型和限位器模型的仿真合理可行.
| [1] | 熊仲明,霍晓鹏,苏妮娜.一种新型基础滑移隔震框架结构体系的理论分析与研究[J].振动与冲击, 2008,27(10):124-129.( 1) 1) |
| [2] | 王社良, 樊禹江, 陈琪,等.基于新型摩擦滑移隔振装置的框架模型地震响应[J].长安大学学报(自然科学版),2014,34(3):92-98.( 1) 1) |
| [3] | 杨佳玲, 王社良, 陈琪.框架结构基础滑移隔震结构地震反应的ANSYS分析[J].水利与建筑工程学报,2012,10(4):145-147.( 1) 1) |
| [4] | 王正林. MATLAB/Simulink与控制系统仿真[M].北京: 电子工业出版社,2012.( 1) 1) |
| [5] | 徐赵东,郭迎庆,周云,等.被动控制结构的Simulink动态仿真分析[J].工程抗震,2000(4):18-22.( 1) 1) |
| [6] | 张威. STATEFLOW逻辑系统建模[M].西安: 西安电子科技大学出版社,2007.( 1) 1) |
| [7] | 王国栋,蒋丽娟,李来平,等.二硫化钼润滑剂应用研究进展[J].中国钼业,2013,37(5):10-14.( 1) 1) |
| [8] | 毛利军,李爱群. 基于SIMULINK的基础滑移隔震结构仿真计算分析[J].东南大学学报(自然科学版),2002,32(5):804-808.( 1) 1) |
| [9] | 熊仲明,张萍萍.滑移隔震结构基于能量分析的简化计算方法研究[J].西安建筑科技大学学报(自然科学版), 2012,44(3):305-309.( 1) 1) |
| [10] | LU X L,ZHOU Q. Dynamic analysis method of a combined energy dissipation system and its experimental verification[J].Earthquake Engineering and Structural Dynamics, 2002,31(6):1251-1265.( 1) 1) |
| [11] | YANG G, SPENCER B F, Jr, CARLSON J D, et al. Large-scale MR fluid dampers modeling and dynamic performance considerations[J].Engineering Structures, 2002, 24( 3):309-323.( 1) 1) |
| [12] | 李树信, 姚谦峰. 软钢实体圆锥棒的限位、消能性能研究[J]. 西安建筑科技大学学报(自然科学版),1992,24(3):243-248.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


