2.清华大学深圳研究生院 能源与环境学部,广东 深圳 518055
2.Division of Energy and Environment, Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, Guangdong, China
供水管网是城市地下的隐形资产,在管道故障诊断过程中,由于管网周围布满基础设施,通过大规模管道开挖技术对管道故障诊断已经不现实,在非开挖技术的引领下,瞬变流故障诊断技术应运而生[1-4].管道腐蚀和阻塞直接体现在管道壁厚改变,管道腐蚀导致管道壁厚变薄,管道阻塞导致管道壁厚变厚.管道阻塞将降低管道输水能力,同时增加输水能量成本[5].检测管道故障的方法有基于流量和化学属性方法[6]、稳态水力学方法[7-8]和在线设施方法[9],但是这些方法对管道壁厚变化定位效率很低.Mphapatra等[10]首次明确提出频域分析在供水管网故障诊断的可行性,对方法进行验证,同时激发更多学者研究频域分析在故障诊断中应用.
Ferrante等[11]通过瞬变流方法对管道淤积进行定位.Duan[12-14]和Stephens等[15]通过瞬变流频域分析,数值模拟管道故障位置.本文建立管道壁厚评估频域响应方程,通过理论和实验的方式对频域响应方程进行验证,对管道壁厚变化进行系统评估.
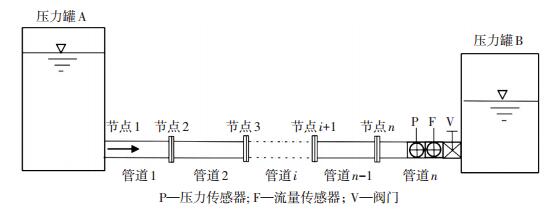
1 频域响应函数理论推导 1.1 频域响应函数理论推导通过连续方程和动量方程在频域范围内变换可以得到管段场矩阵,瞬变流量q和瞬变压力h是关于频域ω的函数,i+1和i分别代表管段L下游和上游(图 1).
|
图 1 管道系统模型 Figure 1 Pipeline system model |
| $ {\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} q\\ h \end{array}\;} \end{array}} \right\}^{i + 1}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {\mu L} \right)}&{\frac{1}{Z}\sin \left( {\mu L} \right)}\\ {{\rm{ - }}Z\sin \left( {\mu L} \right)}&{\cos \left( {\mu L} \right)} \end{array}} \right]{\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} q\\ h \end{array}\;} \end{array}} \right\}^{i}}. $ | (1) |
式中:
Fn为单管场矩阵,系统的场矩阵为系统所有元素矩阵相乘,即
| $ \boldsymbol{U}={\boldsymbol{F}_1}{\boldsymbol{F}_2} \cdot \cdot \cdot {\boldsymbol{F}_{n-1}}{\boldsymbol{F}_n}. $ | (2) |
A和B代表系统管道起始端和末端.通过式(1)和(2)推导得
| $ {q^{\rm{B}}}={U_{11}}{q^{\rm{A}}} + {U_{12}}{h^{\rm{A}}}, $ | (3) |
| $ {h^{\rm{B}}}={U_{21}}{q^{\rm{A}}} + {U_{12}}{h^{\rm{A}}} $ | (4) |
Uij为系统场矩阵U中元素.
假设上游压力恒定(qA=0), 下游水箱压力波动函数为hB=U21qB/U21.当管段N=3,分母为零,获得共振函数表达式
| $ \begin{array}{l} ({Z_1} + {Z_2})({Z_1} + {Z_2})\cos ({\mu _1}{L_1} + {\mu _2}{L_2} + {\mu _3}{L_3}) + \\ ({Z_1}-{Z_2})(-{Z_2}-{Z_3})\cos ({\mu _1}{L_1} + {\mu _2}{L_2} + {\mu _3}{L_3})-\\ ({Z_1} + {Z_2})({Z_2}-{Z_3})\cos ({\mu _1}{L_1} + {\mu _2}{L_2} + {\mu _3}{L_3})-\\ ({Z_1}-{Z_2})(-{Z_2} + {Z_3})\cos ({\mu _1}{L_1} + {\mu _2}{L_2} + {\mu _3}{L_3})=0. \end{array} $ | (5) |
管段壁厚改变位置点矩阵表达形式为
| $ {\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} q\\ h \end{array}\;} \end{array}} \right\}^{i + 1}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ { - \frac{{2\Delta {H_{{\rm{B}}0}}}}{{{Q_{{\rm{B}}0}}}}}&1 \end{array}} \right]{\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} q\\ h \end{array}\;} \end{array}} \right\}^i}. $ | (6) |
式中:ΔHB0为稳态水头损失(m),QB0为稳态流量(L/s).
将U11=cos(μL),U21=-Zsin(μL),式(6)带入式(2)~(4)中得式(7),频域压力(h)关于峰值数目(m)和故障位置(xB*)的表达式为
| $ h=\frac{{2\Delta {H_{\backslash 0}}}}{{\Delta {Q_{\backslash 0}}-\left( {2\Delta {H_{\backslash 0}}\frac{{\left( {\frac{{igA\Delta {H_{{\rm{B}}0}}}}{{a{Q_{{\rm{B}}0}}}} + \frac{{igA\Delta {H_{{\rm{B}}0}}}}{{a{Q_{{\rm{B}}0}}}}\cos \left( {2{\rm{\pi }}x_{\rm{B}}^{^ * }m-{\rm{\pi }}x_{\rm{B}}^ * } \right)} \right)}}{{\left[ {\frac{{-ia}}{{gA}} + \frac{{2\Delta {H_{{\rm{B}}0}}}}{{{Q_{{\rm{B}}0}}}}\sin \left( {2{\rm{\pi }}x_{\rm{B}}^{^ * }m-{\rm{\pi }}x_{\rm{B}}^ * } \right)} \right]}}} \right)}}. $ | (7) |
式中:m为峰值数目,xB*为相对故障位置.
实际计算过程中,2ΔHB0/QB0相对于a/gA较小,可以忽略不计,将式(7)进一步简化为
| $ h=\frac{1}{{\frac{1}{2}{{\left( {\frac{{\Delta {H_0}}}{{{Q_0}}}} \right)}^{-1}} + {{\left( {\frac{a}{{gA}}} \right)}^{-2}}\left( {\frac{{\Delta {H_{{\rm{B}}0}}}}{{{Q_{{\rm{B}}0}}}}} \right)\left[ {1 + \cos \left( {2{\rm{\pi }}x_{\rm{B}}^ * m-{\rm{\pi }}x_{\rm{B}}^ * } \right)} \right]}}. $ | (8) |
通过式(8)中相角绝对值除以π即可得到壁厚变化相对位置xB*.
1.3 壁厚改变长度对共振峰偏移影响管道壁厚改变长度致使管道水力条件改变,所以,根据管道特性参数定义管道壁厚改变长度对管道特性参数影响,通过评估特性参数改变求解壁厚变化长度.当管段壁厚变化时,系统参数将发生改变,例如管道波速(a)、特性阻抗(Z)等参数.定义管道L1和L3完整管道,L2为壁厚改变管道.管道特性阻抗变化定义为δZ=Z2-Z1.管道传播阻抗变化定义为λ1+λ2+λ3-λ0,其中λ=L/a.两个参数的扰动如式(9)和(10),下标“0”表示完整管道(L1和L3).
| $ {\varepsilon _Z}=\frac{{\delta Z}}{{{Z_0}}}=\frac{{{Z_2}-{Z_0}}}{{{Z_0}}}, $ | (9) |
| $ {\varepsilon _\lambda }=\frac{{\delta \lambda }}{{{\lambda _0}}}=\frac{{\left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right)-{\lambda _0}}}{{{\lambda _0}}}=\frac{{{L_2}}}{{{L_0}}}\left( {\frac{{{a_0}}}{{{a_2}}}-1} \right). $ | (10) |
εA=δA/A0、εL=L2/L0和εa=δa/a0分别代表管道截面积、壁厚改变长度和管道波速变化.通过这3个参数定量描述管道壁厚改变长度引起频域峰位置变化,以上3个参数的改变直接影响εZ和ελ两个参数的变化.
将式(9)和(10)带入到式(5)得
| $ \begin{array}{l} \left( {2 + {\varepsilon _Z}} \right)\left( {2 + {\varepsilon _Z}} \right)\cos \left[ {(1 + {\varepsilon _\lambda }){\lambda _0}{\omega _{{\rm{rfb}}}}} \right] + \\ {\varepsilon _Z}\left( {2 + {\varepsilon _Z}} \right)\cos [(1 + {\varepsilon _\lambda }-2\frac{{{\lambda _1}}}{{{\lambda _0}}}){\lambda _0}{\omega _{{\rm{rfb}}}}]-\\ {\varepsilon _Z}\left( {2 + {\varepsilon _Z}} \right)\cos [(1 + {\varepsilon _\lambda }-2\frac{{{\lambda _3}}}{{{\lambda _0}}}){\lambda _0}{\omega _{{\rm{rfb}}}}]-\\ {\varepsilon _Z}^2\cos [(1 + {\varepsilon _\lambda }-2\frac{{{\lambda _2}}}{{{\lambda _0}}}){\lambda _0}{\omega _{{\rm{rfb}}}}]=0. \end{array} $ | (11) |
壁厚改变管道和完整管道相比较,共振峰频率会发生偏移.定义完整管道固有频率为ωrf0,壁厚改变管道频率发生偏移Δωrf.
| $ {\omega _{{\rm{rfb}}}}={\omega _{{\rm{rf}}0}} + \Delta {\omega _{{\rm{rf}}}}. $ | (12) |
为了计算方便,共振峰频率进行泰勒展开,便于对管段共振峰频率近似求解计算.
| $ \begin{array}{l} \cos \left[ {\alpha {\omega _{{\rm{rfb}}}}} \right]=\cos \left[ {\alpha {\omega _{{\rm{rf0}}}}} \right]-\alpha \sin \left[ {\alpha {\omega _{{\rm{rf0}}}}} \right]\Delta {\omega _{{\rm{rf}}}} + \ O\left[ {{{\left( {\Delta {\omega _{{\rm{rf}}}}} \right)}^2}} \right] + \cdot \cdot \cdot \end{array} $ | (13) |
共振峰频域偏移定义如下
| $ \Delta {\omega _{{\rm{rf}}}}=\frac{{{C_u}}}{{{C_u}}}. $ | (14) |
式中:
| $ \begin{array}{l} {C_{\rm{u}}}={\varepsilon _A}\left( {2-{\varepsilon _A}} \right)\sin (2{\lambda _1}{\omega _{{\rm{rf0}}}})-{\varepsilon _A}\left( {2-{\varepsilon _A}} \right).\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \left( {2{\lambda _3}{\omega _{{\rm{rf0}}}}} \right)-\varepsilon _A^2\sin \left( {2{\varepsilon _L}{\lambda _0}{\omega _{{\rm{rf0}}}}} \right), \\ {C_{\rm{d}}}={\left( {2-{\varepsilon _A}} \right)^2} + {\varepsilon _A}\left( {2-{\varepsilon _A}} \right)\left[ {{\lambda _0}-{\lambda _1}} \right]\cos \left( {2{\lambda _1}{\omega _{{\rm{rf0}}}}} \right)-\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _A}\left( {2-{\varepsilon _A}} \right)\left[ {{\lambda _0}-2{\lambda _3}} \right]\cos \left( {2{\lambda _3}{\omega _{{\rm{rf0}}}}} \right)-\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\varepsilon _L}\varepsilon _A^2\cos \left( {2{\varepsilon _L}{\lambda _0}{\omega _{{\rm{rf0}}}}} \right). \end{array} $ |
进一步分析,一般εA < 1,λ1 < λ0和λ3 < λ0,这样Cd=λ0(2-εA)2,管道壁厚改变长度对共振峰偏移影响如下
| $ \begin{array}{l} \frac{{\Delta {\varepsilon _{{\rm{rf}}}}}}{{{\varepsilon _{{\rm{rf0}}}}}} \approx \frac{2}{{\rm{\pi }}}\frac{{{\varepsilon _A}}}{{2-{\varepsilon _A}}} \cdot \{ \sin [(4m-2){\lambda _1}{\varepsilon _{{\rm{th0}}}}]-\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin [(4m-2){\lambda _3}{\varepsilon _{{\rm{th0}}}}]-\cdot \cdot \cdot-\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\varepsilon _A}}}{{2-{\varepsilon _A}}}\sin [(4m-2){\varepsilon _L}{\lambda _0}{\varepsilon _{{\rm{th0}}}}]\}. \end{array} $ | (15) |
式(15)描述了管道壁厚改变对共振峰偏移程度,共振峰偏移是关于正弦的周期函数,共振峰的偏移程度依赖于壁厚改变长度εL和管道横截面积εA.当壁厚变化长度很小,即L2接近于零,εL等于零,Δωrf/ωrf0等于零,满足完整管道共振峰不发生偏移情况,相对于式(5)计算效率会大幅度提高.
2 实验设置 2.1 实验参数设计实验装置:传感器位置、阀门等附属设施设计如图 1所示,实验管道采用DN 40镀锌钢管管材进行实验,下游水箱接口处安装阀门,通过阀门迅速开关产生瞬变流.实验管段总长L=60 m,初始条件如表 1.通过管段异径变化来模拟管段壁厚改变对共振峰影响.
| 表 1 实验初始条件 Table 1 Experimental initial condition |
为了验证管段壁厚变化频域压力函数(h)关于峰值数目(m)和故障位置(xB*)推导准确性,通过实验对式(8)进行验证.变径管段直径DN=32 mm,通过变换管段的位置来模拟壁厚改变位置对频域响应函数影响(图 2),同时根据建立的频域响应函数方程对故障位置进行预测.

|
图 2 壁厚变化位置示意图 Figure 2 Schematic diagram of wall thickness change position |
壁厚改变管道L2仍然采用DN32管道,通过变换管道L2长度验证共振峰偏移方程,L2在6~30 m变换,管道布置详细信息如表 2,表 3为计算系统管段的特性参数.
| 表 2 管段改变长度详细信息 Table 2 Detail information of the length of pipeline changes |
| 表 3 管段壁厚改变长度特性参数计算 Table 3 Characteristic parameter calculation of the length of pipe wall thickness change |
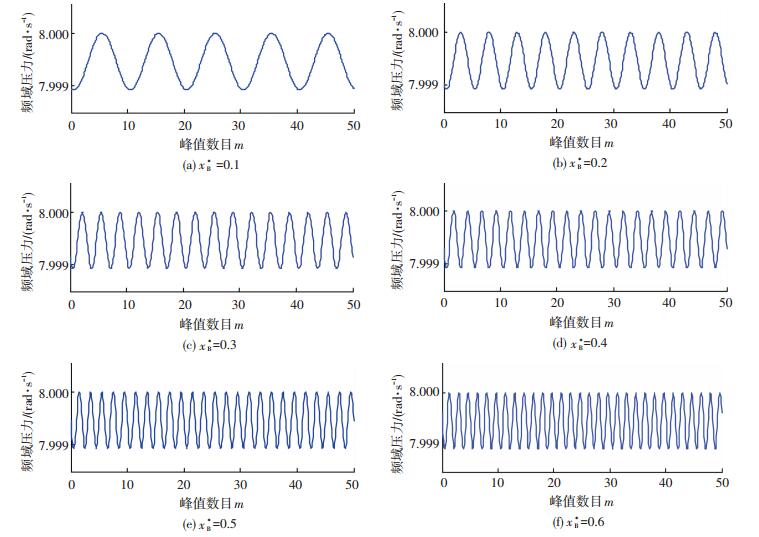
图 3是采集压力信号进行频域变换得到峰值数目(m)函数,伴随故障位置xB*越接近B端压力传感器,频域峰周期变小.通过式(8)和采集压力信号(h,m)可以推导故障位置xB*.一共进行6组实验,分别对xB*=0.1、0.2、0.3、0.4、0.5和0.6进行分析,实验结果和模拟结果见表 4.壁厚变化位置xB*误差分别为0.3%、0.4%、1.13%、0.17%、0.62%和0.37%,定位误差均在2%以内,进一步验证频域响应函数关于管道壁厚变化推导准确性.
|
图 3 采集压力信号关于峰值数目变换 Figure 3 Acquisition pressure signal on the peak number conversion |
| 表 4 管道故障位置实验验证 Table 4 Experimental verification of pipeline fault location |
此外,式(8)中xB*故障位置,根据能斯特定律解释,当壁厚改变相对位置大于0.5时,信号出现的频率位置为(1-xB*).当采样压力进行频域变换时,将得到两个对称的频域峰,同时相角πxB*有正负之分,相角(0≤φ≤π/2)显示故障位置在靠近上游管段位置,相角(-π≤φ≤-π/2)显示故障位置在靠近下游管段位置.
3.2 壁厚变换长度评估通过式(15)对每种情况共振峰偏移进行定量分析,表 5显示了共振峰偏移函数预测结果和实际管段信息.所有管段定位误差均在3%以内,最大误差出现在案例5中,管段阻塞长度L2=30 m,定位长度为29.57 m.
| 表 5 管段壁厚变换长度预测误差 Table 5 Prediction error of the length of pipe wall thickness change |
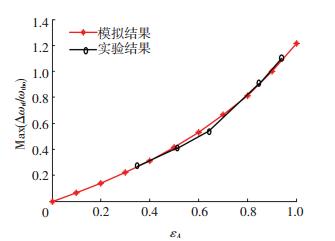
根据式(15)中Δωrf/ωrf0是关于εA/(2-εA)的增函数,为了验证壁厚改变程度对共振峰偏移的影响,将3.2实验中测试管段L2固定为6 m,管径DN为10~32 mm,实验管段详细信息见表 6.管段壁厚改变程度计算信息见表 7.通过变换管道直径模拟壁厚改变程度对共振峰偏移的影响.在数值模拟过程中,管径可以设置为任意数值,然而在实验中仅有5种管径供选择.在图 4中,实验得到共振峰最大偏移曲线和理论计算得到共振峰偏移曲线趋势基本一致.当完整管段εA=0时,最大峰值偏移为0,即共振峰没有发生偏移.当εA=0.5时,最大共振峰偏移接近0.5,接近半个周期的偏移.由于正弦和余弦函数最大值为1,对共振峰偏移影响不大,共振峰偏移函数系数εA/(2-εA)对共振峰偏移影响较大.
| 表 6 管段壁厚改变程度详细信息 Table 6 Detail information of pipeline wall thickness change |
| 表 7 管段壁厚改变程度特性参数计算 Table 7 Characteristic parameter calculation of the degree of pipeline wall thickness change |
|
图 4 壁厚变化程度对共振峰最大偏移影响 Figure 4 Wall thickness varying degree on maximum deviation of resonant peak |
1)推导了共振峰频域响应函数,建立了频域响应压力函数(h)关于峰值数目(m)系统评估方程,相角绝对值除以π即可得到故障发生位置xB*.
2)推导共振峰偏移函数和管道壁厚改变长度之间的关系,对管道壁厚改变长度进行推导.
3)通过监测供水管网瞬变压力在频域范围内变化,根据式(8)和(15)可以计算供水管网壁厚变化位置和长度,进而对供水管网腐蚀和阻塞进行系统评估.
| [1] |
高金良, 李娟娟, 郑志成, 等. 区域供水管网盲源分离漏失量研究[J].
哈尔滨工业大学学报,2015, 47 (6) : 33-37.
GAO Jinliang, LI Juanjuan, ZHENG Chengzhi, et al. Study on leakage of regional distribution network using blind source separation[J]. Journal of Harbin Institute of Technology,2015, 47 (6) : 33-37. (  0) 0)
|
| [2] |
KHULIEF Y, KHALIFA A, MANSOUR R, et al. Acoustic detection of leaks in water pipelines using measurements inside pipe [J]. J PipelineSyst Eng Pract, 2012, 10.1061/(ASCE)PS.1949-1204.0000089, 47-54.
( 0) 0)
|
| [3] |
BROTHERS K J. Water leakage and sustainable supply-truth or consequences?[J].
Journal of AWWA,2001, 93 (4) : 150-152.
( 0) 0)
|
| [4] |
LEE P J, VITKOVSKY J P, LAMBERT M F, et al. Discrete blockage detection in pipelines using the frequency response diagram: numerical study[J].
J Hydraul Eng,2008, 134 (5) : 658-663.
DOI: 10.1061/(ASCE)0733-9429(2008)134:5(658) ( 0) 0)
|
| [5] |
HUNT A. Fluid properties determine flow line blockage potential[J].
Oil Gas J,1996, 94 (29) : 62-66.
( 0) 0)
|
| [6] |
JIANG Y, CHEN H, LI J. Leakage and blockage detection in water network of district heating system[J].
ASHRAE Transactions,1996, 102 (1) : 291-296.
( 0) 0)
|
| [7] |
SCOTT S L, YI J. Flow testing methods to detect and characterize partial blockages in looped subsea flow lines[J].
J Energy Res Technol,1999, 121 (3) : 154-160.
DOI: 10.1115/1.2795975 ( 0) 0)
|
| [8] |
ROGERS L M. Pipeline blockage location by strain measurement using an ROV[C]//Proc Offshore Technology Conf Richardson. TX, 1995:521-528.
( 0) 0)
|
| [9] |
MPHAPATRA P K, CHAUDHRY M H, KASSEM A A, et al. Discussion of detection of partial blockage in single pipelines[J].
J Hydraul Eng,2006, 132 (2) : 200-206.
DOI: 10.1061/(ASCE)0733-9429(2006)132:2(200) ( 0) 0)
|
| [10] |
FERRANTE M, BRUNONE B. Pressure waves as a tool for leak detection in closed conduits[J].
Urban Water Journal,2004, 1 (2) : 145-156.
DOI: 10.1080/1573062042000271073 ( 0) 0)
|
| [11] |
DUAN H F, LEE P J, GHIDAOUI M S, et al. Essential system response information for transient-based leak detection methods[J].
J Hydraul Res,2010, 48 (5) : 650-657.
DOI: 10.1080/00221686.2010.507014 ( 0) 0)
|
| [12] |
DUAN H F, LEE P J, GHIDAOUI M S, et al. System response function based leak detection in viscoelastic pipeline[J].
J Hydraul Eng,2011, 10 : 1061.
( 0) 0)
|
| [13] |
DUAN H F, LEE P J, GHIDAOUI M S, et al. Extended blockage detection in pipelines by using the system frequency response analysis[J].
J Water Resour Plann Manage,2012, 138 : 55-62.
DOI: 10.1061/(ASCE)WR.1943-5452.0000145 ( 0) 0)
|
| [14] |
STEPHENS M, LAMBERT M, SIMPSON A. Determining the internal wall condition of a water pipeline in the field using an inverse transient[J].
J Hydraul Eng,2013, 139 (3) : 310-324.
DOI: 10.1061/(ASCE)HY.1943-7900.0000665 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


