2. 长春工程学院 能源动力工程学院,长春 130012
2. School of Energy and Power, Changchun Institute of Technology, Changchun 130012, China
典塑性热网加热器是电厂热电联产的重要组成设备,是保证电厂供热能力和用户供热质量的关键设备,其性能的好坏直接影响了热电联产的供热量和联产系统的热经济性.热网加热器的热工设计计算主要有两种方法,即平均温差法和效能-传热单元数法.两种方法均需预先设定热网加热器的主要结构,一般通过经验和工艺决定,具有较大的不确定性.同时,在计算传热系数时,需要通过试算确定对流换热系数,为热网加热器的整体设计带来了不确定因素,即便此时的传热系数计算比较准确,由于结构的主观设定,也无法保证热网加热器具有最好的换热性能.目前强化传热理论求解方法主要有熵产分析法、场协同原理及(火积)耗散法.(火积)耗散法可以避免熵产法产生的“熵产悖论”[1],同时比场协同方法简单.(火积)耗散法中的物理量(火积),是过增元教授基于热量与电荷传递现象的类比提出的,用于表示物体传递热量的总能力[2].对于换热器,传热的(火积)耗散法优化主要有两种情况:一种是在给定热流的条件下,寻求变量最优分布使传热温差最小,此时表现为最小(火积)耗散;另一种是在给定温差条件下使传递的热流最大,此时为最大(火积)耗散,二者统称为(火积)耗散极值原理[3].目前,利用(火积)耗散理论强化换热器换热已经取得了较多的研究成果[4-7].
本文以电厂供热系统热网加热器传热过程的(火积)耗散最小为优化目标,实现热网加热器的优化设计.在设计过程中,不预先设定包含换热管外径、换热管数量、换热管长度和蒸汽凝结水温度等热网加热器的具体结构参数,只给出优化过程长径比、流体的流速、换热管数范围和管程与壳程压降等参数需要满足的约束条件,由优化过程寻找最优的结构参数,进而在满足所给定的约束条件下,得到满足换热负荷需求的最佳设计参数.
1 优化模型的建立 1.1 (火积)耗散优化理论过增元等[8]通过热量传递与电荷传递现象之间的比拟,定义了一个描述物体传递热量总能力的新物理量——(火积),定义为(火积)热容量与温度乘积的一半,即
| $ {E_{\rm{h}}} = \frac{1}{2}Q'T.$ | (1) |
式中:Q′为物体的定容热容量,J;T为物体的温度,K.
考虑热网加热器内流体为一维定常流,与外界没有热量交换,建立流体的能量平衡方程为
| $ {C_{\rm{h}}}\frac{{{\rm{d}}T\left( x \right)}}{{{\rm{d}}x}} = - q\left( x \right). $ | (2) |
将上式两侧同时乘以T(x)并在换热器长度方向积分得热、冷流体(火积)平衡式:
| $ \begin{array}{l} \frac{1}{2}{C_{\rm{h}}}T_{{\rm{h,in}}}^2 - \frac{1}{2}{C_{\rm{h}}}T_{{\rm{h,out}}}^2 = \int {q\left( x \right)} {T_{\rm{h}}}\left( x \right)dx,\\ \frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,out}}}^2 - \frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,in}}}^2 = \int {q\left( x \right)} {T_{\rm{c}}}\left( x \right)dx. \end{array} $ | (3) |
式中:q(x)为x处热流量,J;C为流体的热容量流量,J/K;Th(x)、Tc(x)为x处热、冷流体的温度,K;下标in和out分别表示流体的进口和出口.将上两式相加整理得有限温差导热引起的耗散[9]
| $ {E_T} = \left( {\frac{1}{2}{C_{\rm{h}}}T_{{\rm{h,in}}}^2 + \frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,in}}}^2} \right) - \left( {\frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,out}}}^2 + \frac{1}{2}{C_{\rm{h}}}T_{{\rm{h,out}}}^2} \right).$ | (4) |
流动阻力引起的(火积)耗散可表示为[9]
| $ {E_p} = \frac{{{m_{\rm{h}}}\Delta {p_{\rm{h}}}}}{{{\rho _{\rm{h}}}}}\frac{{{T_{{\rm{h,out}}}} - {T_{{\rm{h,in}}}}}}{{\ln {T_{{\rm{h,out}}}} - \ln {T_{{\rm{h,in}}}}}} + \frac{{{m_{\rm{c}}}\Delta {p_{\rm{c}}}}}{{{\rho _{\rm{c}}}}}\frac{{{T_{{\rm{c,out}}}} - {T_{{\rm{c,in}}}}}}{{\ln {T_{{\rm{c,out}}}} - \ln {T_{{\rm{c,in}}}}}}. $ | (5) |
式中:Ep为换热器流动阻力引起的(火积)耗散,m为质量流量,kg/s;ρ为流体密度,kg/m3;Δp为压降,Pa;换热器总(火积)耗散量可表示为
| $ E'={E_T} + {E_p}. $ | (6) |
定义换热器的(火积)耗散与换热器最大(火积)耗散(换热器实际换热量Q′和最大温差Th, in-Tc, in的乘积)之比为(火积)耗散数[10].则(火积)耗散数可表示为
| $ {E^*} = \frac{{E'}}{{Q'\left( {{T_{{\rm{h,in}}}} - {T_{{\rm{c,in}}}}} \right)}} = \frac{{E'}}{{\varepsilon \min \left( {{C_{\rm{h}}},{C_{\rm{c}}}} \right){{\left( {{T_{{\rm{h,in}}}} - {T_{{\rm{c,in}}}}} \right)}^{{2^*}}}}} $ | (7) |
式中ε为换热器的效能.下面便以(火积)耗散最小为优化目标函数,应用粒子群优化算法求解优化问题,建立热网加热器的(火积)耗散最小优化设计方法.
1.2 目标函数以热网加热器的(火积)耗散数最小为优化目标,热网加热器中的总(火积)耗散包括温度(火积)耗散和流动阻力(火积)耗散两部分,温差与流动阻力的(火积)耗散数可分别表示为
| $ \begin{array}{*{20}{l}} {E_T^* = \left( {\frac{1}{2}{m_{{\rm{in}}}}{h_{{\rm{in}}}}{T_{{\rm{h,in}}}} - \frac{1}{2}{c_{{\rm{p,ts}}}}{m_{\rm{h}}}T_{{\rm{ns}}}^2 + \frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,in}}}^2 - \frac{1}{2}{C_{\rm{c}}}T_{{\rm{c,out}}}^2} \right)}\\ {{{\left[ {{m_{\rm{h}}}\left( {{h_{{\rm{h,in}}}} - {h_{{\rm{ns}}}}} \right)} \right]}^{ - 1}} \cdot {{\left( {{T_{{\rm{h,in}}}} - {T_{{\rm{c,in}}}}} \right)}^{ - 1}}.} \end{array} $ | (8) |
| $ \begin{array}{*{20}{l}} {E_p^* = \left( {\frac{{{m_{\rm{h}}}\Delta ph}}{{{\rho _{\rm{h}}}}}\frac{{{T_{{\rm{ns}}}} - {T_{{\rm{h,in}}}}}}{{\ln {T_{{\rm{ns}}}} - \ln {T_{{\rm{h,in}}}}}} + \frac{{{m_{\rm{c}}}\Delta {p_{\rm{c}}}}}{{{\rho _{\rm{c}}}}}\frac{{{T_{{\rm{c,out}}}} - {T_{{\rm{c,in}}}}}}{{\ln {T_{{\rm{c,out}}}} - \ln {T_{{\rm{c,in}}}}}}} \right) \cdot }\\ {{{\left[ {{m_{\rm{b}}}\left( {{h_{{\rm{h,in}}}} - {h_{{\rm{ns}}}}} \right)} \right]}^{ - 1}} \cdot {{\left( {{T_{{\rm{h,in}}}} - {T_{{\rm{c,in}}}}} \right)}^{ - 1}}.} \end{array} $ | (9) |
式中:hh, in为进口蒸汽焓值,J/(kg·s);hns为凝结水焓值,J/(kg·s);Tns为凝结水的温度,K;ρh为热网加热器中蒸汽的密度,kg/m3; Δph和Δpc分别为壳侧与管侧的压降.
则热网加热器的优化目标(火积)耗散数可表示为
| $ f=\min {E^ * }=\min \left({E_T^ * + E_p^ * } \right). $ | (10) |
在常规的热网加热器设计过程中,一般需要首先确定热网加热器的换热管外径do、换热管数Nt、折流板间距h与壳体内径Ds之比Bs、折流板缺口中心角θ、壳侧内径Ds、长径比L/Ds等结构参数.本文将这些参数作为设计变量,给出do、Nt、Bs、L/Ds的约束范围:do, min≤do≤do, max(具体值需按国标选取);Nt, min≤Nt≤Nt, max;Bs, min≤Bs≤Bs, max(按国标取值[11]);(L/Ds)min≤L/Ds≤(L/Ds)max.
热网加热器壳侧内径由下式确定[12]
| $ {D_{\rm{s}}} = \left( {1.1\sqrt {{N_{\rm{t}}} - 1} } \right) \cdot S + 3{d_{\rm{o}}}. $ | (11) |
式中:S为换热管中心距,m;本文的换热管布置选择等边三角形排列.缺口中心角由下式得
| $ \theta = 2\arccos \left( {1 - \frac{{2h}}{{{D_{\rm{s}}}}}} \right).$ | (12) |
壳侧换热流体为蒸汽在水平管外凝结,由于热网加热器中的蒸汽为过热蒸汽,将蒸汽凝结的对流换热系数中的潜热项进行修正,以潜热修正值代替.当管外蒸汽流动雷诺数Rev<3 500时
| $ {\alpha _{\rm{s}}} = 0.725{\left[ {\frac{{g{\rho ^2}\lambda _{\rm{s}}^3r'}}{{{\mu _{\rm{s}}}{N_{\rm{t}}}{d_{\rm{o}}}\left( {{t_{\rm{s}}} - {t_{\rm{w}}}} \right)}}} \right]^{0.25}}. $ | (13) |
式中:ρ为凝结液的密度,kJ/m3;ts为饱和凝结液的温度,K;tw为壁面温度,取进出水温的算术平均值,K.
采用下式计算潜热修正值
| $ r' = {c_{{\rm{ps}}}}\left( {t - {t_{\rm{s}}} + r + {c_{{\rm{pl}}}}\left( {{t_{\rm{s}}} - {t_{{\rm{ns}}}}} \right) + \frac{3}{8}{c_{{\rm{pl}}}}\left( {{t_{{\rm{ns}}}} - {t_{\rm{w}}}} \right)} \right). $ | (14) |
式中:t为进口蒸汽的温度,K;cpl为管内凝结液的定压比热,kJ/(kg·℃);cps为蒸汽的定压比热,kJ/(kg·℃);tns为凝结水的温度,℃;r′为潜热修正值.
1.4 优化算法粒子群优化算法(PSO)是一种用于求解全局优化问题的进化算法.PSO算法首先在可行解区域内随机初始化种群粒子的位置Xi(待求解问题的解)和速度vi,每次迭代过程中,粒子通过跟踪种群全局最优位置(gbest)和当前个体局部最优位置(pbest)来更新[13].粒子的更新按式(15)、(16)完成
| $ {v_{i + 1}}=\omega {v_i} + {c_1}{r_1}\left({{p_{{\rm{Best}}\; i}}-{X_i}} \right) + {c_2}{r_2}\left({{g_{{\rm{Best}}\; i}}-{X_i}} \right). $ | (15) |
| $ {X_{i + 1}} = {X_i} + {v_{i + 1}}. $ | (16) |
式中:c1、c2为加速因子,本文取c1=c2=2,r1、r2为0~1的独立常数,ω为惯性权重.算法中,参数ω、c1、c2的优化选择对算法的收敛性有重要作用,为保证算法的收敛性,必须满足
| $ \max \left({\left| {{\lambda _1}} \right|, \left| {{\lambda _2}} \right|} \right) < 1. $ | (17) |
式中λ1与λ2分别由式(18)和(19)确定,即
| $ {\lambda _1}=\frac{{1 + \omega-{\alpha _1}-{\alpha _2} + \gamma }}{2}, $ | (18) |
| $ {\lambda _2}=\frac{{1 + \omega-{\alpha _1}-{\alpha _2} + \gamma }}{2}. $ | (19) |
式中:γ=[(1+ω-α1-α2)2-4ω]0.5,α1=r1c1,α2=r2c2,且α1+α2的取值范围在0~4,ω在0~1.与以往研究中惯性权重取为定值不同,本文将ω进行如下改进
| $ \omega=\left({\omega-0.1} \right)\left({1-\frac{{当前粒子代数}}{{粒子总代数}}} \right) + 0.1. $ | (20) |
热网加热器粒子群优化算法的实现步骤如下:
1)初始化种群的粒子参数,优化过程中种群的粒子数等于优化变量的数量,粒子的最大迭代数为50,随机粒子在相应变量的约束范围内取一组初值Xi=f(do, Nt, Bs, L/Ds);
2)根据目标函数式(10)计算各粒子的适应度值,将当前各粒子的位置和适应值设定在pBest中,将所有pBest中适应值最优个体的位置和适应值存储于gBest中;
3)应用式(15)、(16)更新粒子的速度和位置,并计算粒子的适应度值,按更新后的粒子适应度值排序;
4)对每个粒子,将其适应值与其经过的最好位置进行比较,如果较好,则将其作为当前的最优位置;
5)比较当前所有pBest和gBest值,更新gBest;
6)若满足程序停止的条件(本文采取迭代次数限制),搜索停止,输出结果,否则返回步骤3)继续搜索.
2 算例与分析某热网加热器的热工已知参数见表 1.
| 表 1 热网加热器热力参数 Table 1 Parameters of the heater for heating network |
基于(火积)耗散优化设计方法对某厂家热网加热器的结构及热力参数进行优化计算,根据热网加热器热力参数和厂家样本,给定设计变量的约束范围如下:
1)换热管外径do,16≤do≤35 mm;
2)换热管数Nt,800≤Nt≤1 500;
3)Bs按国家标准,在0.2≤Bs≤1.0范围内取值[11];
4)长径比L/Ds:选取在6≤L/Ds≤10范围内,热网加热器壳侧内径由式(11)确定.
此外考虑流体的流速与流体物理性质和污垢热阻有关,气体流速vs与液体流速vt分别作如下限定,3 < vt < 15 m/s, 0.2 < vs < 1.5 m/s; 并且管程压降Δpc与壳程压降Δph分别满足Δph < 5×104 Pa,Δpc < 5×104 Pa.
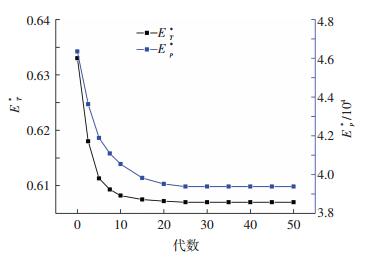
根据上述的优化已知条件和约束范围,按照粒子群优化算法的计算步骤,计算出(火积)耗散数随粒子代数的变化规律(见图 1).温差引起的(火积)耗散与流动阻力引起的(火积)耗散均随粒子代数的增大而先减小,在第20代粒子后,两耗散值趋于稳定,表明粒子群优化算法具有良好的快速收敛性能.优化计算的结果,得出热网加热器的结构参数(见表 2).
| 表 2 (火积)耗散优化方法下的最优结构 Table 2 Optimal structure under the entransy optimization method |
|
图 1 (火积)耗散随粒子代数变化 Figure 1 Curves of entransy dissipation with the particles generations |
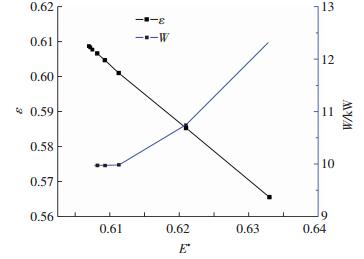
图 2为优化过程中不同(火积)耗散数时热网加热器的效能与功耗,其中热网加热器的功耗由下式确定:
| $W = \frac{1}{{1000\eta }}\left( {\frac{{{m_{\rm{h}}}}}{{{\rho _{\rm{h}}}}}\Delta {p_{\rm{h}}} + \frac{{{m_{\rm{c}}}}}{{{\rho _{\rm{c}}}}}\Delta {p_{\rm{c}}}} \right). $ | (21) |
|
图 2 效能与功耗随(火积)耗散数变化 Figure 2 Curves of performance and power consumption with the entransy dissipation |
式中:W为换热过程的动力消耗,kW;η为泵的效率.
由于热网加热器蒸汽侧具有相变,传热有效度可表示为
| $ \varepsilon = \frac{{{T_{{\rm{c,out}}}} - {T_{{\rm{c,in}}}}}}{{{T_{{\rm{h,in}}}} - {T_{{\rm{c,in}}}}}}. $ | (22) |
由图 2可以看出,优化过程中,热网加热器的效能随(火积)耗散数增大而减小,且变化规律近似线性.总(火积)耗散数最小时对应的换热效能为0.609,此时热网加热器的热力性能最优,热网加热器功耗也为整个优化过程的最小值9.92 kW,即采用本文的(火积)耗散优化,当热网加热器的热力性能最优时,其功耗达最小值.
为证明本文优化计算方法的优越性,采用常规方法对上述热网加热器进行设计计算,根据表 1热网加热器的热力参数,结合热网加热器厂家提供的样本,选取的结构参数见表 3.
| 表 3 热网加热器结构参数 Table 3 Structure parameters of the heater for heating network |
为进一步与常规设计方法的计算结果进行比较,计算了部分热网加热器的热工性能,并将计算结果进行对比,结果见表 4.可以看出,与常规方法相比,采用(火积)耗散优化设计受换热管数与换热管长减少的影响,热网加热器功率消耗由12.34 kW降为9.92 kW,下降了19.61%;效能由0.565增大为0.609,增加了7.79%.优化后的管侧流体速度增大而壳侧流体速度减小,导致管侧的对流换热系数αt增加了4.7%,壳侧对流换热系数减小了2.8%.同时,优化后温差和阻力引起的(火积)耗散均有所减小.通过优化设计发现,当热网加热器的热力性能最优时,其功耗达最小值.优化后热网加热器的换热管径为30 mm,高于常规方法的25 mm,虽然换热管数略有减少,但总换热面积增大,这一结果说明本优化方法是以增大换热面积为代价的.总体来说,基于(火积)耗散优化方法设计出的热网加热器的性能优于常规方法.
| 表 4 常规方法与(火积)耗散优化方法性能参数比较 Table 4 Performance parameter comparison of the conventional method and the entransy optimization method |
以(火积)耗散数为目标的热网加热器优化设计,实现了在不预先设定热网加热器结构的条件下,确定其最优的结构设计参数,弥补了传统设计方法的不足.可为实际工程中热网加热器的优化设计提供理论指导,同时,本文的优化方法对其他换热器的优化设计具有可推广性.
| [1] |
HESSELGREAVES J E. Rationalisation of second law analysis of heat exchanger[J].
International Journal of Heat Mass Transfer,2000, 43 (22) : 4189-4204.
DOI: 10.1016/S0017-9310(99)00364-6 ( 0) 0)
|
| [2] |
GUO Zengyuan, ZHU Hongye, LIANG Xingang. Entransy:a physical quantity describing heat transfer ability[J].
International Journal of Heat and Mass Transfer,2007, 50 (13) : 2545-2556.
( 0) 0)
|
| [3] |
李志信, 过增元.
对流传热优化的场协同理论[M]. 北京: 科学出版社, 2010 .
LI Zhixin, GUO Zengyuan. Field synergy theory of the optimized convective heat transfer[M]. Beijing: China Science Publishing, 2010 . (  0) 0)
|
| [4] |
GUO Jiangfeng, XU Mingtian, CHENG Lin. Principle of equipartition of entransy dissipation for heat exchanger design[J].
Science China Techno-logical Sciences,2010, 53 (5) : 1309-1314.
DOI: 10.1007/s11431-010-0128-y ( 0) 0)
|
| [5] |
ZHU Wensheng, KUK Anthony, GUO Jianhua. Haplotype inference for population data with genotyping errors[J].
Biom J,2009, 51 (4) : 644-658.
DOI: 10.1002/bimj.v51:4 ( 0) 0)
|
| [6] |
XIA Shaojun, CHEN Lingen, SUN Fengrui. Optimization for entransy dissipation minimization in heat exchanger[J].
Chinese Science Bulletin,2009, 54 (19) : 3587-3595.
( 0) 0)
|
| [7] |
XU Mingtian, GUO Jiangfeng, CHENG Lin. Application of entransy dissipation theory in heat convection[J].
Frontiers of Energy and Power Engineering in China,2009 (4) : 402-405.
( 0) 0)
|
| [8] |
程雪涛, 梁新刚, 过增元. 孤立系统内传热过程的(火积)减原理[J].
科学通报,2011, 56 (3) : 847-854.
CHENG Xuetao, LIANG Xingang, GUO Zengyuan. Entransy decrease principle of heat transfer in an isolated system[J]. Chin Sci Bull,2011, 56 (3) : 847-854. (  0) 0)
|
| [9] |
许明田, 程林, 郭江峰. 耗散理论在换热器设计中的应用[J].
工程热物理学报,2009, 30 (12) : 2090-2092.
XU Mingtian, CHENG Lin, GUO Jiangfeng. Application of entransy dissipation theory in heat exchanger design[J]. Journal of Engineering Thermophysics,2009, 30 (12) : 2090-2092. (  0) 0)
|
| [10] |
GUO Jiangfeng, XU Mingtian. The application of entransy dissipation theory in optimization design of heat exchanger[J].
Applied Thermal Engineering,2012, 36 : 227-235.
DOI: 10.1016/j.applthermaleng.2011.12.043 ( 0) 0)
|
| [11] |
史美中, 王中铮.
热交换器原理与设计[M]. 南京: 东南大学出版社, 2009 .
SHI Meizhong, WANG Zhongzheng. Principle and design of heat exchangers[M]. Nanjing: Southeast University Press, 2009 . (  0) 0)
|
| [12] |
KREITH F.
CRC handbook of thermal engineering[M]. Florida: CRC Press, 2000 .
( 0) 0)
|
| [13] |
FVD B, ENGELBRECHT A P. A study of particle swarm optimization particle trajectories[J].
Information Sciences,2006, 176 (8) : 937-971.
DOI: 10.1016/j.ins.2005.02.003 ( 0) 0)
|
 2016, Vol. 18
2016, Vol. 18


