低温流体如液氢、液氧等被广泛地用于液体火箭发动机推进系统中.发动机涡轮泵高速旋转时会使得叶片周围流体介质发生压降,当压力降低到当地饱和蒸汽压强以下时会引起空化的发生[1-2].汽化潜热的存在使得空化相变过程产生汽-液两相间热量的传递,即空化热力学效应[3].常温水空化过程通常被视为等温过程,而低温流体介质物理属性对温度变化敏感,使得热力学效应在低温流体空化过程中表现较为显著[4-5].空化现象直接影响着火箭发动机推力的大小,同时也是制约发射成功与否的关键因素之一,所以掌握低温流体空化的流动特性及其预示方法显得尤为重要.
Stahl等[6]最早提出了B因子理论,分析了热力学效应对泵的扬程的影响;后来Sarosdy等[7]开展了水和氟利昂空化的对比试验,发现了氟利昂液体空化时空泡呈泡雾状态特性;20世纪70年代Hord[8]系统地开展液氢和液氮的低温空化试验,从而加深对低温流体空化特性的直观认识.但是由于低温流体工作环境的限制,大大增加了试验流场参数的测试难度.近些年数值计算成为研究低温流体空化的主要手段, Hosangadi等[9]采用Merkle空化模型对液氢和液氮流体空化流动进行了计算,但是在空化闭合区域计算结果与试验差值较大;Tseng[10]、马相孚[11]、张小斌[12]和黄彪[13]等对入口黏度、质量传输模型参数敏感性等因素对空化流场结果影响进行了分析,但都是二维数值模拟计算.开展三维数值计算可有效获取空化流场参数,加深对低温流体空化特性的全面认识.
本文通过CEL (CFX expression language)语言将Schnerr-Sauer空化模型嵌入到CFX软件中,并将液氮、液氢的密度、比热容、热传导系数以及饱和蒸汽压强等随温度变化的物性参数引入到求解代码中;同时考虑空化过程汽化潜热的影响,并将其以源相的形式添加到能量方程中,从而形成了一套计算低温流体空化的三维数值方法,为后续开展全模型诱导轮空化提供技术支撑.同时获得的液氢和液氮空化流场参数为今后液体火箭发动机推进系统的设计提供参考.
1 数值计算方法 1.1 基本控制方程和湍流闭合方法对于考虑热力学效应的低温空化流动问题计算的控制方程,除了连续性方程和动量方程外,还包括包含能量源项的能量方程,依次如下:
| $ \begin{array}{l} \frac{{\partial {\rho _m}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left({{\rho _m}{u_j}} \right)=0, \frac{\partial }{{\partial t}}\left({{\rho _m}{u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left({{\rho _m}{u_i}{u_j}} \right)=\\-\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left({\mu + {\mu _t}} \right)\left({\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right], \\ \frac{{\partial \left({{\rho _m}{c_p}T} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left({{\rho _m}{u_j}{c_p}T} \right)=\\ \nabla \cdot \left({{k_{eff}}\nabla T} \right)-\frac{{\partial \left({{\rho _m}{f_v}L} \right)}}{{\partial t}}-\frac{{\partial \left({{\rho _m}{u_j}{f_v}L} \right)}}{{\partial {x_j}}}. \end{array} $ |
式中:ρm=αlρl+αvρv为混合相的密度;下标v和l分别代表汽相和液相;下标i和j分别代表坐标方向;u为速度;μ为流体的动力黏度;μt是湍流黏度;keff为热传导系数;L为汽化潜热;cp为比定压热容.
选取k-ε两方程模型作为湍流闭合方法,通过求解湍动能和湍流耗散值可有效预测空化流场湍流特性.
1.2 空化模型在物理上空化过程是由热力学和动力学约束的相变过程,通过建立汽-液两相之间质量传输的蒸发源相(
| $ \frac{\partial }{{\partial t}}\left({{\alpha _v}{\rho _v}} \right) + \nabla \cdot \left({{\alpha _v}{\rho _v}{{\overrightarrow u }_m}} \right)={\dot m^ + }-{\dot m^-}. $ |
式中, ρv随温度变化的属性通过自定义函数引入到CFX中,计算过程中ρv对应于当地温度下的密度值.
Schnerr-Sauer空化模型[14]主要是基于Rayleigh-Plesset汽(气)泡动力学方程(1)的推导,得到描述汽(气)泡生长和溃灭的基本方程:
| $ \frac{{{p_v}-p}}{{{\rho _t}}}=R\frac{{{d^2}{{\Re}_B}}}{{d{t^2}}} + \frac{3}{2}{\left({\frac{{d{{\Re}_B}}}{{dt}}} \right)^2} + \frac{{2\zeta}}{{{\rho _l}R}}. $ | (1) |
式中:pv为泡内压强;p为气泡周围流场压强;R为汽泡半径;ρl为液体密度;ζ为液体表面张力.忽略方程(1)右侧的二次项和表面张力项可得表征空化过程气泡半径\ReB的变化方程:
| $ \frac{{{\rm{d}}{\Re _B}}}{{{\rm{d}}t}} = \sqrt {\frac{2}{3}\frac{{\left( {{p_v} - p} \right)}}{{{p_l}}}.} $ |
基于上述分析得到Schnerr-Sauer空化模型中的蒸发源相和凝结源相表达式为:
| $ {\dot m^-}=\frac{{{\rho _v}{\rho _l}}}{{{\rho _m}}}{\alpha _v}\left({1-{\alpha _v}} \right)\frac{3}{{{{\Re}_B}}}\sqrt {\frac{2}{3}\frac{{\left({{p_v}\left(T \right)-p} \right)}}{{{\rho _l}}}, } $ | (2) |
| $ \begin{array}{l} {{\dot m}^ + } = \frac{{{\rho _v}{\rho _l}}}{{{\rho _m}}}{\alpha _v}\left( {1 - {\alpha _v}} \right)\frac{3}{{{\Re _B}}}\sqrt {\frac{2}{3}\frac{{\left( {p - {p_v}\left( T \right)} \right)}}{{{\rho _l}}}} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p > {p_v}\left( T \right). \end{array} $ | (3) |
式中, pv(T)为远处流场当地温度下的饱和蒸汽压强.
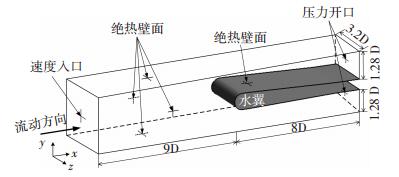
1.3 计算模型液氢和液氮绕水翼空化计算模型与Hord试验一致,试验结构及尺寸如图 1所示.根据试验条件,计算域入口采用速度入口,出口为压力开口,流域边界及水翼设置为绝热不可滑移壁面,且各个边界位置初始液相体积分数设置为1,汽相体积分数为0.同时并在翼型表面分别设置5个温度监测点和5个压力监测点,以便将数值计算结果与试验数据进行对比.
|
图 1 计算域及边界条件 Figure 1 Computational domain and boundary conditions |
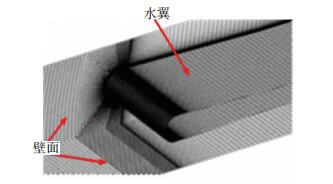
图 2给出了计算模型网格划分,计算域内采用H-型和C-型网格,以提高计算效率;同时在水翼附近网格进行加密处理,以有效捕捉翼型周围流场参数,网格总数量为104万,且在计算过程中对网格无关性进行了验证.
|
图 2 计算网格划分 Figure 2 Mesh generation around hydrofoil |
根据Hord试验数据随机选取4种不同工况,其入口流速Uint、远场温度T∞和入口空化数σint如表 1所示.计算过程中保持计算网格、湍流模型、边界条件以及试验参数等条件一致.通过对比两种介质下空化区域两相分布特性、翼型周围压力和温度数据等综合参数,分析液氢和液氮空化特性的差异.
| 表 1 计算工况 Table 1 Simulation cases and run conditions |
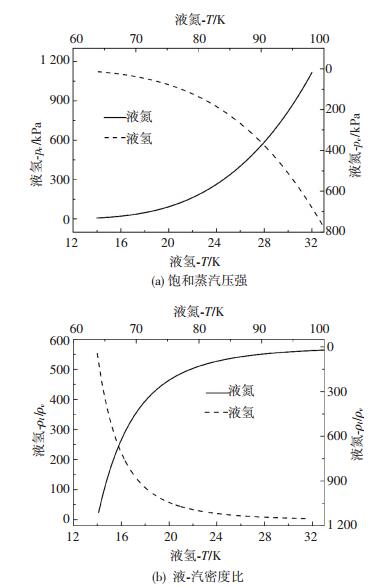
为更好地对比分析热力学效应下液氢和液氮空化特性,图 3给出了两种介质中汽化压强和液-汽密度比随温度变化曲线.针对本文计算工况,当液氢温度在20.5 K时,液-汽密度比为50,当温度降低1 K时,汽化压强减小28 kPa;当液氮温度在83 K时,液-汽密度比为95,当温度降低1 K时,汽化压强减小18 kPa[15].
|
图 3 液氢和液氮随温度变化的物理属性 Figure 3 Physical properties of liquid hydrogen and nitrogen |
表 2对比了两种温度下液氮和液氢的比定压热容、密度比、热传导系数以及汽化潜热等物性参数.
| 表 2 液氢和液氮部分物性参数比较 Table 2 Comparison of the physical properties of liquid hydrogen, liquid nitrogen and water |
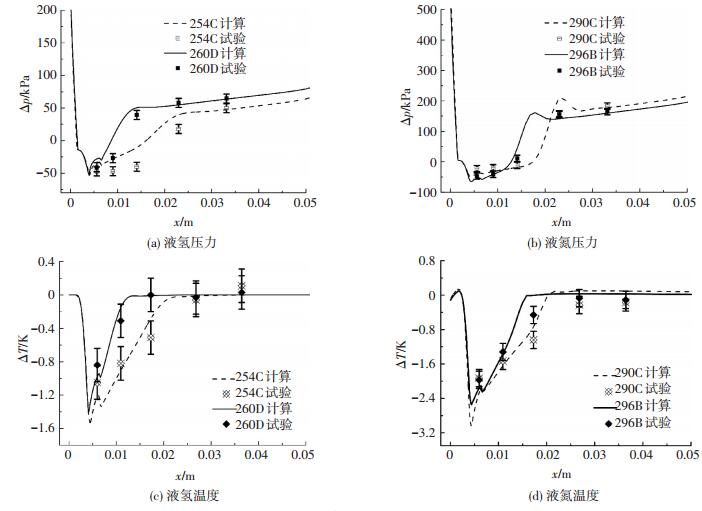
图 4给出了翼型表面压力和温度分布的数值计算结果与试验数据对比,其中定义压降Δp=p-pv(T∞),温降ΔT=T-T∞.考虑到Hord试验测量过程中温度不确定误差为0.2 K,液氢和液氮的压力测量误差分别为6.90 kPa和10.34 kPa,可知数值计算得到的温降和压力分布与试验结果吻合较好,从而验证了数值计算方法的有效性.当水翼周围发生空化时,由于汽化潜热的影响使得空化过程不断从周围流体吸收热量,从而导致空化区域的温度降低,空化强度的差异使得空化区域温度分布不同,即体现为液氢和液氮发生空化时水翼周围表现为Δp<0和ΔT<0,而在常温水空化时温降和压降可忽略不计.在液氢254C和260D工况中,254C工况在空化闭合区域压力恢复到远场压力梯度较小,低压区域较大;液氮290C和296B工况中,虽然296B工况入口空化数较小,但其空化区域较小,最大压降低于290C工况,可见当入口空化数较小时热力学效应抑制作用更明显,所以在液氮空化中入口空化数不能充分体现空化强度的大小.
|
图 4 数值计算结果与试验数据对比 Figure 4 Comparison of numerical results and experimental data |
对比图 4中液氢和液氮压力和温度分布可知,在液氮空化低压区压力恢复到远场压强的压力变化梯度明显较大,且在空化闭合区域出现压力峰值,这可能是空泡闭合位置汽液之间质量传输特性的差异引起的;对比温降数据,可以看出液氮在空化区域温降较大.在空化热力学敏感介质中,最大压降和温降百分比是评价热力学影响的重要参数之一,根据图 4的计算结果,表 3总结了4种工况下最大压降(Δp|=(pmin-pv(T∞))/pv(T∞))和温降(|ΔT|=(Tmin-T∞)/T∞)百分比数据.4种工况下虽然空化数接近,但是液氢最大压降百分比超过40%,最大温降百分比大于6%,二者数值均约为液氮的两倍,可见热力学效应明显改变空化区域流场参数的分布,且热力学效应对液氢空化特性的影响更加显著.
| 表 3 压降Δp和温降ΔT最大百分比 Table 3 Maximum percentage of pressure and temperature depression% |
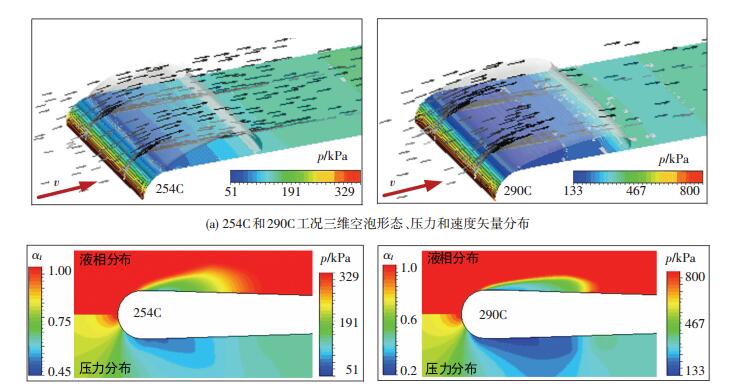
为进一步对比分析两种介质空化特性的差异,图 5给出了254C和290C工况稳态计算空化流场特性对比.图 5(a)两种工况下三维空泡形态沿水翼跨度方向基本呈均匀对称分布,均形成了稳定的空泡,从图中也可初步看出二者空泡形态稍有差异,在254C液氢工况计算的空泡较厚.同时图 5(a)也给出了水翼表面压力场分布,可见压力沿水翼跨度方向(图 1中z轴)基本呈对称均匀分布,压力在水翼前缘最大,在水翼靠近前缘位置形成低压区,并沿流动方向压力逐渐恢复.从图中可以看出290C工况低压区域分布较大,在空化闭合区域压力梯度变化较大,在空泡内部水翼表面压力等值线呈U型分布,可见在三维计算中可获得壁面效应对空泡形态和压力分布的影响.图 5(a)也给出了流场内部速度矢量分布图,可以看出在靠近水翼前缘位置速度变化梯度较大,在空泡内部及闭合位置没看到明显的回射流现象.
|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第8期) 图 5 液氢和液氮空化流场特性对比 Figure 5 Comparison of cavitation characteristics in liquid hydrogen and nitrogen |
为更有效对比空泡特征,图 5(b)给出了254C和290C工况在水翼中截面压力分布(下半区域)和液相体积分数分布(上半区域).从压力云图分布可以进一步看出254C工况低压区域覆盖范围较小,压力沿在水翼周围变化梯度不明显.在低温状态下空化区域压力分布实际反映着空泡内两相分布特性,空泡内在液相向汽相转化过程中,由于发生温降,使得空泡压强与当地温度下饱和蒸汽压强直接相关;同时液氮高密度比(见图 3)和空化时温降值较大(见图 4),从而导致液氮空化流场压力梯度变化明显.
从图 5(b)可知两种工况下空泡长度基本一致,但是空泡形态轮廓和液相体积分数分布有所差异.两种工况下水翼表面液相最小体积分数都大于零,这主要是由于低温液氢和液氮属性对温度变化敏感,同时液-汽密度比值较小,使得在质量传输过程中液相向汽相转换不充分,这与参考文献[9, 13, 16]中结果一致.在液氢254C工况中空泡形态近似呈椭圆形,液相最小体积分数为0.45,在空化闭合区域汽相向液相转换的凝结过程缓慢,表现为液相体积分数变化梯度较小.而在液氮290C工况中空泡最大厚度发生在空化下游区域,空泡内液相最小体积分数比液氢中小,最小值为0.2,可见在水翼周围空化强度较大,同时在空泡尾部闭合位置汽相向液相转化的体积分数变化梯度较大,这也进一步解释了液氢空化闭合区域压力变化缓慢和液氮空化空泡尾部出现压力峰值的原因.同时根据Hord实验观测,液氮和液氢空泡呈不透明的泡雾状,这与水空化空泡汽液界面清晰有明显不同,计算得到图 5(b)中体积分数分布特性有效地解释了液氮/液氢空泡呈泡雾状现象问题.
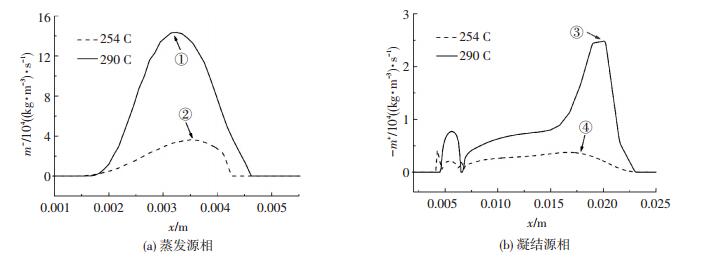
空化过程汽液两相间质量传输率对流场分布特性具有重要影响,为深入分析上述计算结果,图 6给出了254C和290C工况水翼表面蒸发源相和凝结源相的分布曲线.可以看出两种介质中蒸发源相m-明显大于凝结源相m+,从而证明了低温流体中汽化过程速度要比凝结过程快得多,这与常温水中的结论一致.
|
图 6 液氢和液氮空化质量传输率对比 Figure 6 Comparison of interphase mass transfer rate in liquid hydrogen and nitrogen |
在图 6(a)中最大蒸发率发生在x=0.003 5位置(图中①和②),结合图 4压力和温度变化曲线,可知最大温降和压降发生在空化区域最大蒸发率位置.
图 6(b)中290C工况凝结源相峰值(图中③位置)明显较大,且曲线变化陡峭,即体现为液氮空化时在空泡尾部闭合区域汽-液两相间传输剧烈,从而引起该区域压力出现峰值(见图 4(a))、液相体积分布变化迅速(见图 5(b)).不同工况的计算结果均表明液氮的m-和m+大于液氢,图 6(a)液氮在①位置值约为液氢在②位置的4倍,而根据图 3中两种介质属性,290C工况T=83 K时,液-汽密度比为95,液氢254C工况T=20.5 K时,液-汽密度比为50,两种工况操作温度下液氮液汽密度比约为液氢的2倍,可见液汽密度比不能完全反映出空化过程两相间质量传输,结合式(2)~(3)可知空化区域两相密度、体积分数以及压力分布等因素综合影响着液汽两相间质量转化的大小.
3 结论1)建立了液氢和液氮绕三维水翼空化的数值计算方法.对比空化区域压力和温度分布的数值结果和试验数据,在测量误差范围内两者体现了较好的一致性,从而验证了计算方法的有效性.
2)热力学效应对两种介质空化区域温度和压力影响程度不同.热力学效应引起液氮和液氢空化区域发生压降和温降,但是在空化数相近时,液氢的最大温降和压降百分比为液氮的2倍.
3)流体介质物理属性影响着空化区域汽液两相分布特性.液氢在空化区域液相体积分数较大,且在空泡闭合区域液汽两相间转化缓慢;液氮在空泡尾部闭合区域液相体积分数变化迅速.
4)汽液两相间质量传输特性体现着流场参数的分布.最大压降和温降发生在蒸发率最大位置;液氮中空泡闭合位置的凝结源相的突变反映此空化区域压力在恢复到远场压力过程中变化梯度较大,同时引起该区域液相体积分布变化迅速.
| [1] |
BATCHELOR G K.
An introduction to fluid dynamics[M]. UK: Cambridge University Press, 2000 .
( 0) 0)
|
| [2] |
JOSEPH D D. Cavitation in a flowing liquid[J].
Physical Review E,1995, 51 (3) : R1649-R1650.
DOI: 10.1103/PhysRevE.51.R1649 ( 0) 0)
|
| [3] |
WATANABE S, HIDAKA T, HORIGUCHI H, et al. Analysis of thermodynamic effects on cavitation instabilities[J].
Journal of Fluids Engineering,2007, 129 (9) : 1123-1130.
DOI: 10.1115/1.2754326 ( 0) 0)
|
| [4] |
TSENG C C, WEI Yingjie, WANG Guoyu, et al. Modeling of turbulent, isothermal and cryogenic cavitation under attached conditions[J].
Acta Mechanica Sinica,2010, 26 (3) : 325-353.
DOI: 10.1007/s10409-010-0342-7 ( 0) 0)
|
| [5] |
马相孚.低温流体空化特性数值研究[D].哈尔滨:哈尔滨工业大学, 2013.
MA Xiangfu. Numerical study on cavitating flow of cryogenic fluids[D]. Harbin: Harbin Institute of Technology, 2013. (  0) 0)
|
| [6] |
STAHL H A, STEPANOFF A J. Thermodynamic aspects of cavitation in centrifugal pumps[J].
ASME Journal of Basic Engineering,1956, 78 (8) : 1691-1693.
( 0) 0)
|
| [7] |
SAROSDY L R, ACOSTA A J. Note on observations of cavitation in different fluids[J].
Transactions of the ASME,1961, 83 (3) : 399-400.
DOI: 10.1115/1.3658979 ( 0) 0)
|
| [8] |
HORD J. Cavitation in liquid cryogens II-hydrofoil: NASA Contractor Report: CR-2156[R]. Washington, DC: NASA. 1973.
( 0) 0)
|
| [9] |
HOSANGADI A, SCIENTIST P, AHUJA V, et al. Numerical study of cavitation in cryogenic fluids[J].
Journal of Fluids Engineering,2005, 127 (2) : 267-281.
DOI: 10.1115/1.1883238 ( 0) 0)
|
| [10] |
TSENGC C, SHYY W. Modeling for isothermal and cryogenic cavitation[J].
International Journal of Heat and Mass Transfer,2010, 53 (1) : 513-525.
DOI: 10.1016/j.ijheatmasstransfer.2009.09.005 ( 0) 0)
|
| [11] |
MA Xiangfu, WEI Yingjie, WANG Cong, et al. Simulation of liquid nitrogen around hydrofoil cavitation flow[J].
Journal of Ship Mechanics,2012, 16 (12) : 1345-1352.
( 0) 0)
|
| [12] |
ZHANG Xiaobin, WU Zhao, XIANG Shijun, et al. Modeling cavitation flow of cryogenic fluids with thermodynamic phase-change theory[J].
Chinese Science Bulletin,2013, 58 (4/5) : 567-574.
DOI: 10.1007/s11434-012-5463-x. ( 0) 0)
|
| [13] |
HUANG Biao, WU Qin, WANG Guoyu. Numerical investigation of cavitating flow in liquid hydrogen[J].
International Journal of Hydrogen Energy,2014, 39 (4) : 1698-1709.
DOI: 10.1016/j.ijhydene.2013.11.025 ( 0) 0)
|
| [14] |
SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics [C]//Proceedings of the 4th International Conference on Multiphase Flow. New Orleans:[s.n.], 2001.
( 0) 0)
|
| [15] |
LEMMON E W, HUBER M L, MCLINDEN M O. Reference fluid thermodynamic and transport properties [DB/M]. NIST Standard Reference Database 23, Version 7.0, 2002.
( 0) 0)
|
| [16] |
SUN Tiezhi, WEI Yingjie, WANG Cong, et al. Three-dimensional numerical simulation of cryogenic cavitating flows of liquid nitrogen around hydrofoil[J].
Journal of Ship Mechanics,2014, 18 (12) : 1434-1443.
DOI: 10.3969/j.issn.1007-7294.2014.12.003 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


