超空泡技术能极大降低水下航行体的摩擦阻力,使其获得巨大的速度优势,因此受到世界各海军强国的广泛关注[1-2].然而超空泡航行体的流体动力特性与常规水下航行体相比有着显著不同,沾湿面积的减少、浮力的损失、空泡与航行体间强烈的非线性作用等复杂因素给其动力学建模、机动及稳定控制带来了极大的困难[2-3].超空泡航行体的运动大致可分为加速段及巡航段。在巡航阶段,由于速度、空化数保持恒定,空泡完全包裹整个航行体,仅有尾部由于航行体摆动等原因浸入水中,因此航行体流体动力特性相对稳定;与巡航段不同,在加速阶段航行体的运动特性更加复杂,空泡尺寸、沾湿面积、空化数等参数变化剧烈.国内外目前有关超空泡航行体控制问题的研究一般都着眼于其巡航阶段.如文献[4]对超空泡航行体纵平面内控制的基准问题进行了研究,该文献中提出的二自由度动力学模型被广泛采用;文献[5]基于文献[4]的模型,采用反步法设计了状态反馈控制器,实现了对超空泡航行体的稳定控制;文献[6]改进了文献[4]的模型,并基于保代价控制理论设计了自适应滑模控制器;文献[7]对文献[4]中的模型进行了修正,考虑了空泡记忆效应的影响,设计了双闭环控制系统.上述文献的研究均主要针对巡航阶段,而关于加速阶段的研究鲜有报道.
本文主要针对超空泡航行体加速运动阶段的动力学及控制问题进行了研究.利用细长体理论详细计算了航行体加速过程中各区域流体动力,进而建立了更加精确的非线性动力学模型,并基于精确线性化方法设计了深度跟踪控制器,实现了超空泡航行体加速段变空化数条件下的深度跟踪.
1 超空泡航行体加速段动力学模型本文主要研究超空泡航行体加速段纵平面内的运动.典型的超空泡航行体主要由头部圆盘空化器、圆锥段、圆柱段及尾翼组成.如图 1所示将航行体表面根据沾湿程度不同划分为空泡全包裹区、部分沾湿区及全沾湿区.为分别计算航行体各区域的流体动力,必须首先确定不同时刻的空泡形态及轴线的偏移情况.
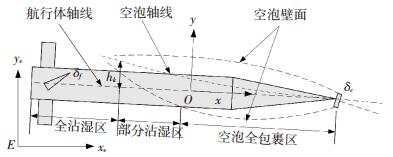
|
图 1 超空泡航行体沾湿区域划分示意 Figure 1 Scheme of immersion state of supercavitating vehicle |
对空泡形态的准确预测是流体动力计算的基础.在实际运动过程中,空泡轴线受到空泡记忆效应、重力、空化器偏转及攻角的影响会产生不同程度的偏轴量.因此需对空泡形态计算进行一定的修正.
1.1.1 空泡形态计算Logvinovich[8]基于空泡截面独立膨胀原理及大量的试验给出了未受扰动情况下空泡形态计算公式为
| $ {R_c}\left(x \right)=\left\{ \begin{array}{l} {R_n}{\left({1 + \frac{{3x}}{{{R_n}}}} \right)^{\frac{1}{3}}}, x \le {x_1};\\ {R_k}\sqrt {1-\left({\frac{{R_1^2}}{{R_k^2}}} \right){{\left({1-2\frac{{x-{x_1}}}{{{L_k}-2{x_1}}}} \right)}^2}, } x > {x_1}. \end{array} \right. $ |
式中:Rc为空泡半径;Rn为空化器半径,x1=1.92Rn;空泡最大半径
由空泡截面独立膨胀原理可知,空泡的各个截面按照空化器的运行轨迹各自独立扩展,与空化器在这一瞬间前后的运动状态无关,仅与空化器通过该截面瞬时的速度、阻力、空泡内外压差等参数相关.空泡的这种特点被称为空泡的记忆效应[8].假设t时刻空化器中心的深度为yc(t),而空化器经过空泡某一截面的时刻为t-τ,t-τ时刻空化器中心的深度为yc(t-τ),则由于空泡记忆效应引起的空泡偏轴量可表示为
| $ {h_m}={y_c}\left({t-\tau } \right)-{y_c}\left(t \right). $ | (1) |
式中:时延τ≈x/v(其中v为航行体速度).
在弗劳德数Fr较小的情况下,空泡在重力场中受到浮力的作用会产生一定程度的“上漂”,其偏轴量hg可表示为[9]:
| $ \begin{array}{l} {h_g} = \frac{{\left( {1 + \sigma } \right){x^2}}}{{3F{r^2}}},Fr = \frac{v}{{\sqrt {g{L_k}} }},\\ 0.05 \le \sigma \le 0.10,2.0 \le Fr \le 3.5. \end{array}$ | (2) |
式中:Fr以空泡全长作为特征长度,g为重力加速度.
空化器攻角引起的空泡轴线偏移又被称为空化器的定向效应[8],其偏轴量hc可表示为
| $ {h_c}=-\frac{{2{F_{cl}}}}{{\rho {v^2}\pi {R_n}}}\left({0.46-\sigma + \frac{{2x}}{{{L_k}}}} \right), $ | (3) |
式中Fcl为空化器升力.
此外,航行体的攻角引起的空泡轴线偏移hα计算公式为
| $ {h_\alpha }=x\tan \; \alpha. $ | (4) |
综合式(1)~(4)可得空泡轴线相对于航行体轴线总偏移量hk为
| $ {h_k}={h_m} + {h_g} + {h_c} + {h_\alpha }. $ | (5) |
超空泡航行体在加速段主要受力有空化器和尾翼的升力与阻力、部分沾湿区的滑行力及全沾湿区流体动力(见图 1).由于气体密度较小,空泡全包裹区所受空气动力可以忽略不计.
1.2.1 空化器及尾翼受力空化器一方面可以诱导空泡的产生,另一方面用于提供航行体稳定航行所需的头部升力.如图 2所示,可以将空化器表面所受流体动力分解为沿速度轴方向的阻力Fcd和升力轴方向的升力Fcl,根据文献[4],阻力系数Cd与升力系数Cl均是空化器攻角αc的函数为
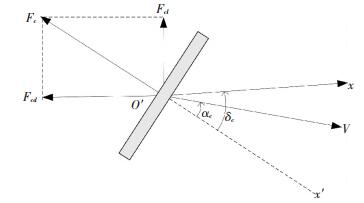
|
图 2 空化器所受流体动力示意 Figure 2 Hydrodynamics forces acting on the cavitator |
| $ \left\{ \begin{array}{l} {C_d}={c_{x0}}\left({1 + \sigma } \right){\cos ^2}{\alpha _c}, \\ {C_l}={c_{x0}}\left({1 + \sigma } \right)\cos \; {\alpha _c}\sin \; {\alpha _c}. \end{array} \right. $ | (6) |
式中cx0为零空化数阻力系数.
表 1为不同空化器锥角条件下cx0的实验值与理论计算值的比较[10],本文所采用的是圆盘空化器,即锥角为90°,则cx0取实验值为0.82.
| 表 1 不同锥角情况下cx0的实验值与理论值对比 Table 1 Drag coefficient cx0of cone cavitator at different cone angles |
空化器中心O′处的垂向速度可表示为航行体垂向速度vy与点O′绕航行体质心旋转的线速度xcωz之和,进一步可得速度轴与空化器法线O′x′之间的夹角为
| $ {\alpha _c}={\delta _c}-\frac{{{v_y} + {x_c}{\omega _z}}}{v}. $ | (7) |
式中:δc为空化器转角;vy为垂向速度;xc为空化器相对于航行体坐标系的坐标;ωz为俯仰角速度.
根据式(6)~(7),可得空化器阻力Fcd与升力Fcl表达式为
| $ \left\{ \begin{array}{l} {F_{cd}}=-\frac{1}{2}\rho \pi R_n^2{v^2}{c_{x0}}\left({1 + \sigma } \right), \\ {F_{cl}}=-\frac{1}{2}\rho \pi R_n^2{v^2}{c_{x0}}\left({1 + \sigma } \right)\left({-\frac{{{v_y} + {x_c}{\omega _z}}}{v} + {\delta _c}} \right). \end{array} \right. $ | (8) |
式中ρ为水的密度.
将尾翼看作是一个特殊的楔形空化器,仿照式(8)给出尾翼阻力及升力表达式为[7]
| $ \left\{ \begin{array}{l} {F_{fd}}=-\frac{1}{2}\rho \pi R_n^2{v^2}{c_{x0}}n\left({1 + \sigma } \right), \\ {F_{fl}}=-\frac{1}{2}\rho \pi R_n^2{v^2}{c_{x0}}\left({1 + \sigma } \right)n\left({-\frac{{{v_y} + {x_f}{\omega _z}}}{v}} \right) + {\delta _c}. \end{array} \right. $ |
式中:n为尾翼升力相对空化器升力的相似系数;xf为尾翼相对于航行体坐标系的坐标;δf为尾翼转角.
1.2.2 部分沾湿区受力部分沾湿区所受滑行力是航行体流体动力中最复杂的.文献[11-12]基于Wagner关于圆柱体在曲面滑行的理论得到了垂直于航行体轴线方向的滑行力表达式.在此基础上,结合式(5)对空泡轴线偏移的计算,给出部分沾湿区滑行力估算公式如下:
| $ \begin{array}{l} {F_p}=\frac{1}{2}\rho {v^2}\pi R_c^2\sin {\alpha _p}\cos \; {\alpha _p} \cdot \\ \left[ {1-{{\left({\frac{{{R_c}-r}}{{{h_p} + {R_c}-r}}} \right)}^2}} \right]\left({\frac{{r + {h_p}}}{{r + 2{h_p}}}} \right), \\ {\alpha _p}=\arctan \left({{h_k}/x} \right), \\ {h_p}=\left| {{h_k}} \right|-\left| {{R_c}-r} \right|. \end{array} $ |
式中:r为滑行位置处航行体截面半径;hp为浸入深度;αp为航行体轴线与空泡轴线间的夹角.
部分沾湿区所受黏性摩擦力及力矩可表示为:
| $ \begin{array}{l} {F_{pf}}=-\frac{1}{2}\rho {v^2}\; {\cos ^2}{\alpha _p}{S_p}{C_p}, \\ {M_{pf}}=-\frac{1}{2}\rho {v^2}\; {\cos ^2}{\alpha _p}{S_p}{y_{pf}}{C_p}. \end{array} $ |
式中:Sp为部分沾湿区沾湿面积;ypf为沾湿面积中心在y轴的坐标;Cp为部分沾湿区黏性系数.
1.2.3 全沾湿区受力将全沾湿区划分为一系列切片微元,根据细长体理论,每个切片所受横向力fw可表示为[13-14]
| $ {f_w}=-\frac{1}{2}\rho D{C_w}\left({{v_y} + {\omega _z}x} \right)\left| {{v_y} + {\omega _z}x} \right|. $ | (9) |
式中:D为航行体直径,Cw为全沾湿区黏性系数.
对式(9)沿航行体轴线方向积分可得全沾湿区横向力及力矩为:
| $ \begin{array}{l} {F_w}=\int\limits_{{x_w}}^{{x_p}} {{f_w}dx}, \\ {M_w}=\int\limits_{{x_w}}^{{x_p}} {{f_w}xdx}. \end{array} $ |
式中:xp、xw分别为全沾湿区第1个与最后1个切片坐标.
此外,全沾湿区黏性摩擦力可表示为:
| $\begin{array}{l} {F_{wf}}=-\frac{1}{2}\rho {v^2}\pi {R^2}{C_w}, \\ {C_w}=\frac{{0.075}}{{{{\left({\lg \; Re-2} \right)}^2}}}\frac{{{\Omega _w}}}{{\pi {R^2}}}. \end{array} $ |
式中Ωw为全沾湿区面积.
1.3 纵向运动模型建立如图 1所示的地面坐标系xeEye及航行体坐标系xOy.假设航行体为理想刚体,质量保持恒定,在纵平面内的运动为小角度机动,且推力为常量.基于对空泡形态的预测及航行体各区域流体动力计算,结合动量、动量矩定理及相应的运动学方程,建立超空泡航行体加速段纵平面内运动的简化数学模型.可得仿射形式的系统方程如下
| $ \left\{ \begin{array}{l} \boldsymbol{\dot x}=\boldsymbol{f\left(x \right)} + \boldsymbol{g\left(x \right)u}, \\ \boldsymbol{y}=\boldsymbol{h}\left(\boldsymbol{x} \right). \end{array} \right. $ | (10) |
其中
| $ \begin{array}{l} \boldsymbol{x}=\left[ {\begin{array}{*{20}{c}} {{y_e}}\\ \theta \\ {{v_x}}\\ {{v_y}}\\ {{\omega _z}} \end{array}} \right]\boldsymbol{f}\left(\boldsymbol{x} \right)=\left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ {{f_3}}\\ {{f_4}}\\ {{f_5}} \end{array}} \right], \boldsymbol{g}\left(\boldsymbol{x} \right)=\left[ {\begin{array}{*{20}{c}} 0 & 0\\ 0 & 0\\ 0 & 0\\ {-\frac{{{F_{cd}}}}{m}} & {-\frac{{{F_{fd}}}}{m}}\\ {-\frac{{{F_{cd}}{x_c}}}{{{J_z}}}} & {-\frac{{{F_{fd}}{x_f}}}{{{J_z}}}} \end{array}} \right], \\ \boldsymbol{u}=\left[ {\begin{array}{*{20}{c}} {{\delta _c}}\\ {{\delta _f}} \end{array}} \right], \boldsymbol{h}\left(\boldsymbol{x} \right)=\left[ {\begin{array}{*{20}{c}} {{y_e}}\\ \theta \end{array}} \right], \boldsymbol{y}=\left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right].\\ {f_1}={v_x}\theta + {v_y}, {f_2}={\omega _z}, \\ {f_3}=-g\theta + \frac{T}{m} + \frac{{{F_{cd}}}}{m} + \frac{{{F_{fd}}}}{m} + \frac{{{F_{pf}}}}{m} + \frac{{{F_{wf}}}}{m}, \\ {f_4}=-g-{v_x}{\omega _z} + \frac{{{F_p}}}{m} + \frac{{{F_w}}}{m}-\frac{{{F_{cd}}\left({{v_y} + {x_c}{\omega _z}} \right)}}{{mv}}-\\ \frac{{{F_{fd}}\left({{v_y} + {x_f}{\omega _z}} \right)}}{{mv}}, \\ {f_5}=\frac{{{F_p}{x_p}}}{{{J_z}}} + \frac{{{M_w}}}{{{J_z}}} + \frac{{{M_{pf}}}}{{{J_z}}} + \frac{{{M_w}}}{{{J_z}}}-\frac{{{F_{cd}}{x_c}\left({{v_y} + {x_c}{\omega _z}} \right)}}{{{J_z}v}}-\\ \frac{{{F_{fd}}{x_f}\left({{v_y} + {x_f}{\omega _z}} \right)}}{{{J_z}v}}. \end{array} $ |
在设计控制器之前,首先对系统的开环运动进行分析.航行体的结构参数按照文献[4]中给定,令推力T为常量,初始时刻深度ye为2 m,轴向速度vx为50 m/s,即
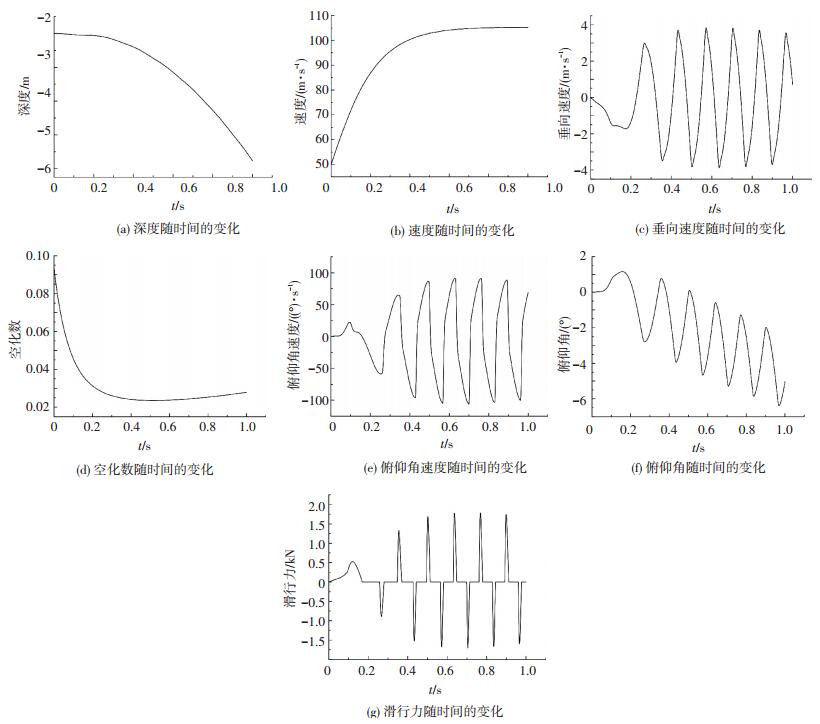
|
图 3 系统开环响应曲线 Figure 3 Response in the uncontrolled case |
从图 3中可以看出,航行体在加速运动过程中,由于空泡的包裹使航行体失去了部分浮力,而空化器及尾翼均无偏转,无法提供足够的升力,因此航行深度在重力作用下持续增加.航行体速度在恒定推力作用下不断变大,随着阻力的增加,速度最终趋向于稳定.与之相应,空化数则是先变小而后趋于稳定.航行体在运动过程中与空泡的上下壁面发生周期性的碰撞,因此垂向速度与俯仰角速度基本保持等幅振荡,俯仰角则在振荡的同时持续增加.
滑行力是超空泡航行体所受流体动力中最复杂的一种.如图 3(g)所示,初始阶段空化数较大,空泡仅能包裹部分航行体表面,由于重力作用,此时部分沾湿区的下表面首先与水接触从而产生向上的滑行力.该阶段航行体表面始终与空泡壁面保持接触,因此滑行力是连续的.此后随着空化数的减小,空泡尺寸不断增大直至能够包裹整个航行体.同时,航行体尾部在空泡内不断摆动,反复穿透空泡上下壁面,滑行力呈现周期性的变化.
从上述对系统的开环特性分析可知,系统在无控制输入条件下不存在平衡点,无法维持稳定状态.因此有必要加入反馈控制,使航行体能够维持稳定运动.
2.2 基于精确线性化的最优控制设计针对式(10)所示数学模型存在强非线性项及动态耦合与操纵耦合严重的特点,本文采用精确线性化方法对其进行输入输出线性化[15],然后根据最优控制理论设计深度跟踪控制器.
通过求解李导数可得系统的相对阶r1=r2=2,ri是使yi(ri)表达式中有输入出现的最小整数,则
| $ y_i^{\left({{r_i}} \right)}=L_f^{{r_i}}{h_i} + \sum\limits_{j=1}^2 {{L_{{g_j}}}L_f^{{r_i}-1}{h_i}{u_j}, } $ | (11) |
将r1与r2代入式(11)中,可得
| $ \left[ \begin{array}{l} {{\ddot y}_1}\\ {{\ddot y}_2} \end{array} \right]=\left[ \begin{array}{l} L_f^2{h_1}\left(\boldsymbol{x} \right)\\ L_f^2{h_2}\left(\boldsymbol{x} \right) \end{array} \right] + \boldsymbol{A}\left(\boldsymbol{x} \right)\left[ \begin{array}{l} {\delta _c}\\ {\delta _f} \end{array} \right]. $ | (12) |
式中:
| $ \boldsymbol{A}\left(\boldsymbol{x} \right)=\left[ {\begin{array}{*{20}{c}} {{L_{g1}}{L_f}{h_1}} & {{L_{g2}}{L_f}{h_1}}\\ {{L_{g1}}{L_f}{h_2}} & {{L_{g2}}{L_f}{h_2}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{{C_1}}}{m}} & {\frac{{{C_2}}}{m}}\\ {\frac{{{C_1}{L_c}}}{{{J_z}}}} & {\frac{{{C_2}{L_c}}}{{{J_z}}}} \end{array}} \right]. $ |
由于A(x)可逆,则取输入变换可得
| $ \boldsymbol{u}=\left[ {\begin{array}{*{20}{c}} {{\delta _c}}\\ {{\delta _f}} \end{array}} \right]={\boldsymbol{A}^{-1}}\left(\boldsymbol{x} \right)\left[ {\begin{array}{*{20}{c}} {{v_1}-L_f^2{h_1}\left(x \right)}\\ {{v_2}-L_f^2{h_2}\left(x \right)} \end{array}} \right], $ |
将输入代入式(12)可得
| $ \left[ {\begin{array}{*{20}{c}} {{{\ddot y}_1}}\\ {{{\ddot y}_2}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}} \end{array}} \right] $ |
引入新的状态变量
| $ \left\{ \begin{align} & \boldsymbol{\dot{\bar{x}}}=\boldsymbol{A}\boldsymbol{\bar{x}}+\boldsymbol{Bv}, \\ & \boldsymbol{y}=\boldsymbol{C}\boldsymbol{\bar{x}}. \\ \end{align} \right. $ | (13) |
式中:
设期望轨迹为r(t),跟踪误差
| $ \boldsymbol{\dot \mu} \left(t \right)={\boldsymbol{A}_\mu }\boldsymbol{\mu} \left(t \right) + {\boldsymbol{B}_\mu }\boldsymbol{\delta} \left(t \right). $ | (14) |
式中:
针对式(14)选取二次型性能指标函数为
| $ J=\frac{1}{2}\int \begin{array}{l} \infty \\ 0 \end{array} \left({{\boldsymbol{\mu} ^T}\left(t \right)\boldsymbol{Q}\boldsymbol{\mu} \left(t \right) + {\boldsymbol{\delta} ^T}\left(t \right)\boldsymbol{R\delta} \left(t \right)} \right)dt. $ |
可得线性二次型最优状态反馈控制器如下
| $ \boldsymbol{\delta} \left(t \right)=-{\boldsymbol{R}^{-1}}\boldsymbol{B}_\mu ^T \boldsymbol{P\mu} \left(t \right), $ | (15) |
式中, P为满足Riccati方程的正定对称矩阵.
将式(15)代入υ的表达式中,给出控制输入u的最终表达式为
| $ \begin{array}{l} \boldsymbol{u}=\left[ \begin{array}{l} {\delta _c}\\ {\delta _f} \end{array} \right]={\boldsymbol{A}^{-1}}\left(\boldsymbol{x} \right)\left({\boldsymbol{\ddot r}-{\boldsymbol{R}^{-1}}\boldsymbol{B}_\mu ^T \boldsymbol{P\mu} \left(t \right)-} \right.\\ \; \;\; \;\; \left. {\left[ \begin{array}{l} {k_2}{\mu _2} + {k_1}{\mu _1} + {v_x}{f_2} + \theta {f_3} + {f_4}\\ \; \;\; \;\; \;\; \;\; {k_4}{\mu _4} + {k_3}{\mu _3} + {f_5} \end{array} \right]} \right). \end{array} $ |
取初始状态
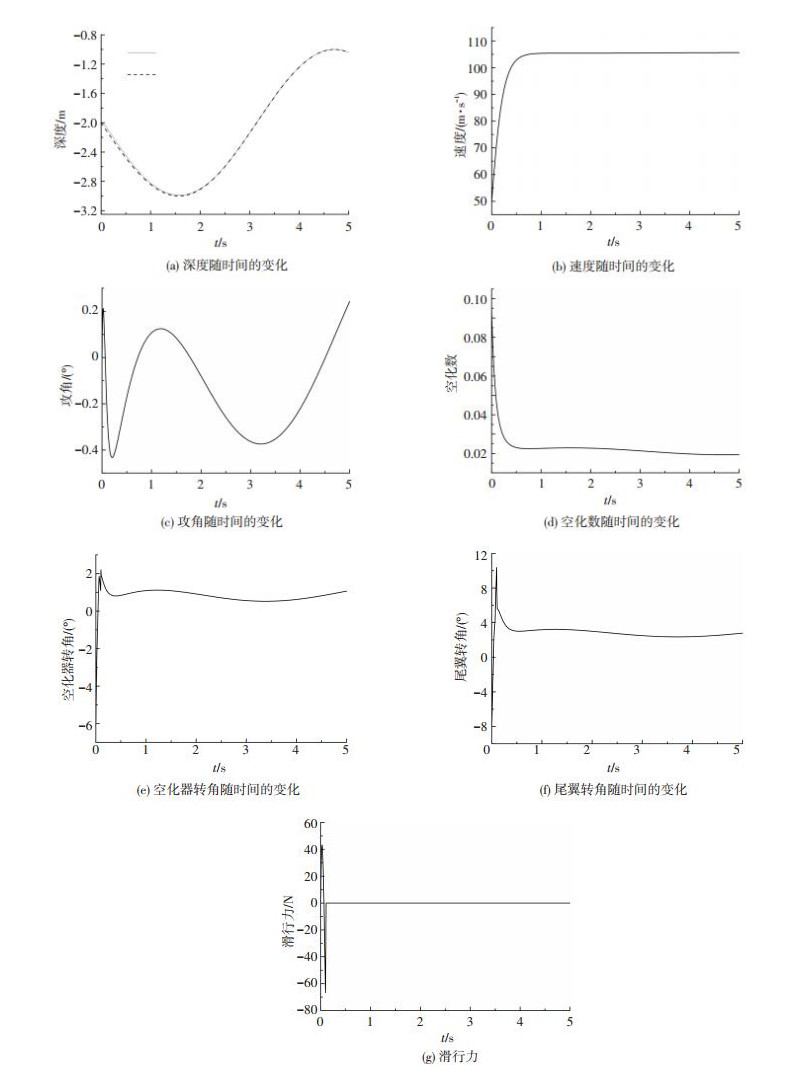
|
图 4 深度跟踪响应曲线 Figure 4 Response curve of depth track |
从图 4可以看出,初始阶段由于攻角为正,航行深度略大于期望深度,而后系统在控制器调节下迅速改变航行深度趋向指定深度信号,较好地实现了对深度信号的跟踪任务.跟踪误差小于2%,满足控制精度要求.同时,攻角被限制在0.4°以内,满足小角度假设.
受初始阶段空化数剧烈变化的影响,控制面在初始阶段输出幅值较大,并存在一定程度的振荡,随后迅速趋于平缓.实际系统中控制面的转角范围是受限制的,算例中空化器转角小于6°,尾翼转角小于10°,均在实际执行机构可以容许的范围以内.
在初始约0.1 s内滑行力短暂出现,其幅值小于60 N,较无控状态下大幅减小.之后在控制输入作用下航行体与空泡的相对位置固定,其运动始终稳定在空泡内,因此滑行力持续为零.
3 结论1)控制器在航行体加速阶段空化数变化剧烈的情况下依然能够很好地完成跟踪任务,跟踪误差小于2%,满足控制精度的要求.
2)控制过程中空化器转角小于6°,尾翼转角小于10°,控制变量的输出均在实际执行机构允许的范围之内,具有良好的实用性.
3)滑行力在控制器作用下大幅减小,约0.1 s后滑行力变为零,航行体的运动被稳定在空泡内部,有利于提高航行稳定性及减小因滑行而产生的摩擦阻力.
| [1] |
曹伟, 魏英杰, 王聪, 等. 超空泡技术现状、问题与应用[J].
力学进展,2006, 36 (4) : 571-579.
DOI: 10.3321/j.issn:1000-0992.2006.04.008 CAO Wei, WEI Yingjie, WANG Cong, et al. Current status, problems and applications of supercavitation technology[J]. Advances in Mechanics,2006, 36 (4) : 571-579. DOI: 10.3321/j.issn:1000-0992.2006.04.008 (  0) 0)
|
| [2] |
SANABRIA D E, BALAS G J, ARNDT R E A. Planing avoidance control for supercavitating vehicles[C]//The 2014 American Control Conference. Portland, OR: IEEE, 2014: 4979-4984. DOI:10.1109/ACC.2014.6859485.
( 0) 0)
|
| [3] |
KIRSCHNER I N, UHLMAN J S, PERKINS J B. Overview of high-speed supercavitating vehicle control[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Colorado: AIAA, 2006: 3100-3116. DOI: 10.2514/6.2006-6442.
( 0) 0)
|
| [4] |
DZIEISKI J, KURDILA A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J].
Journal of Vibration and Control,2003, 9 (7) : 791-804.
DOI: 10.1177/1077546303009007004 ( 0) 0)
|
| [5] |
QIANG Baochen, SUN Yao, HAN Yuntao, et al. Absolute stability control of supercavitating vehicles based on backstepping[C]//International Conference on Mechatronics and Automation. Tianjin: IEEE, 2014: 1918-1923. DOI:10.1109/ICMA.2014.6885995.
( 0) 0)
|
| [6] |
LV Rui, YU Kaiping, WEI Yingjie, et al. Adaptive robust controller for supercavitating vehicle using guaranteed cost theory[J].
Journal of Harbin Institute of Technology (New Series),2011, 18 (4) : 77-81.
( 0) 0)
|
| [7] |
VANEK B, BOKOR J, BALAS G J, et al. Longitudinal motion control of a high-speed supercavitation vehicle[J].
Journal of Vibration and Control,2007, 13 (2) : 159-184.
DOI: 10.1177/1077546307070226 ( 0) 0)
|
| [8] |
LOGVINOVICH G V.
Hydrodynamics of flow with free boundaries[M]. Kiev: Naukova Dumka, 1969 .
( 0) 0)
|
| [9] |
黄海龙, 魏英杰, 黄文虎, 等. 重力场对通气超空泡影响的数值模拟研究[J].
哈尔滨工业大学学报,2007, 39 (5) : 800-803.
DOI: 10.3321/j.issn:0367-6234.2007.05.031 HUANG Hailong, WEI Yingjie, HUANG Wenhu, et al. Numerical simulation study of the influence of gravity field on the ventilated supercavity[J]. Journal of Harbin Institute of Technology,2007, 39 (5) : 800-803. DOI: 10.3321/j.issn:0367-6234.2007.05.031 (  0) 0)
|
| [10] |
NEAVES M D, EDWARDS J R. All-speed time-accurate underwater projectile calculation using a preconditioning algorithm[J].
Journal of Fluids Engineering,2006, 128 (2) : 284-296.
DOI: 10.1115/1.2169816 ( 0) 0)
|
| [11] |
GOEL A. Robust control of supercavitating vehicles in the presence of dynamic and uncertain cavity[D]. Gainesville, FL:University of Florida, 2005.
( 0) 0)
|
| [12] |
VASIN A D, PARYSHEV E V. Immersion of a cylinder in a fluid through a cylindrical free surface[J].
Fluid Dynamics,2001, 36 (2) : 169-177.
DOI: 10.1023/A:1019299930896 ( 0) 0)
|
| [13] |
李杰, 鲁传敬, 陈鑫, 等. 附着空泡对潜射导弹弹道影响分析[J].
弹道学报,2014, 26 (3) : 54-58.
DOI: 10.3969/j.issn.1004-499X.2014.03.012 LI Jie, LU Chuanjing, CHEN Xin, et al. Analysis on influence of attached cavity on the trajectory of submarine launched missile[J]. Journal of Ballistics,2014, 26 (3) : 54-58. DOI: 10.3969/j.issn.1004-499X.2014.03.012 (  0) 0)
|
| [14] |
NEWMAN J N.
Marine hydrodynamics[M]. Cambridge: The MIT Press, 1977 .
( 0) 0)
|
| [15] |
贺昱曜, 闫茂德.
非线性控制理论及应用[M]. 西安: 西安电子科技大学出版社, 2007 .
HE Yuyao, YAN Maode. Nonlinear control theory and applications[M]. Xi'an: Xidian University Press, 2007 . (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


