随着地下储气库调峰技术在全球天然气调峰手段中所占比例逐渐增大,各国温室气体减排任务的逐年加重[1~2],将CO2注入地下储气库做垫层气技术的优势逐渐显现,得到许多国家的高度重视和大力推广[3].目前,中国建成并投入使用的25座天然气地下储气库年工作气量为30×108 Nm3,总设计工作气量为257×108 Nm3[4].据中国“十三五”规划[5],到2020年,地下储气库的总调峰工作气量将达440×108 Nm3,若按照1∶1的储气库垫层气与工作气比例、且CO2垫层气占总库容的30 %计算[6~7],将有264×108 Nm3的温室气体深埋于地下,并替代出相应的天然气,将大大降低地下储气库建设的初投资,带来可观的经济效益和社会效益.
目前,中国已投入使用和正在建设的地下储气库绝大部分为枯竭油气藏改建而成[8],然而,地下油气藏在开采后期由于经常采用加压注水开采和加压压裂开采等气田增产方式,导致气藏储层内微裂缝数量大大增加,气藏停产后经常被水侵.因此,当枯竭气藏改建为储气库时,如何保证气水界面稳定是储气库建设和运行的核心问题之一[9-10].如何保证储气库在建库扩容阶段注CO2垫层气稳定驱水扩容和在季节调峰阶段气水边界的动态平衡尤为重要.CO2做天然气储气库垫层气是作者于2005年首次提出并实际论证的[11],十多年来,在CO2做垫层气的可行性、CO2与天然气共存与混合、储气库的多井优化运行等方面研究较多[7, 12~15],随着研究的深入和实际工程的探索应用,在低渗水淹气藏改建储气库中CO2垫层气与边水之间的溶解与界面稳定运移等问题较为突出,亟待解决.
在低渗透储层扩容建库时,CO2逐渐驱边水渗流,由于储层渗透率差异、各注采井运行参数不同等原因,气水边界会出现指进、舌进等现象,导致界面运移不稳定;当储气库进行城市调峰时,由于储层压力降低,部分CO2会因溶解度下降而从边水中析出,影响气水边界的稳定性.为此,根据枯竭气藏型双重孔隙介质储层特性及三维两相渗流理论和CO2的溶解特性,建立了CO2与边水的气水两相渗流数值模型,利用相应的离散和数值求解方法,得到储层内压力和饱和度的控制方程、CO2在边水中的溶解方程,求得储层内各点的瞬态压力场和饱和度场,进而计算得到相应的气水界面.分析CO2注入方式对扩容建库阶段和季节调峰阶段气水界面运移的影响,得到储气库扩容建库和季节调峰时边缘气井的注采控制策略,为地下储气库建库扩容和季节调峰运行提供技术支撑.
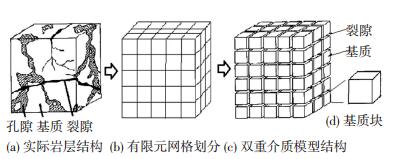
1 数学模型的建立与求解在双重孔隙介质模型中,认为基质孔隙和裂缝孔隙均布于储层内且相互独立,基质为气体的主要储存空间,裂隙为渗流通道,两者之间存在质量交换.将实际裂缝性储层中的裂隙、基质和储层骨架做如图 1所示的简化,并基于以下几条基本假设建立相应数值模型[16]:
|
图 1 双重介质储层的模型简化示意图 Figure 1 Simplified model view of dual medium reservoir |
1)基质网格块之间不存在渗流流动,且互不连通;2)流体在低渗储层中的渗流存在启动压力梯度;3)气水边界处只考虑CO2与水的气水驱替过程,认为天然气不与边、底水接触;4)储层具有非均质性和各向异性;5)储层基质不可压缩,而流体可压缩;6)储层处于等温状态,不考虑温度对气体动力黏度等参量的影响.
1.1 控制方程组的建立1)连续性方程
裂缝系统
| $-\nabla \cdot \left({{\rho _{\rm{g}}}{v_{\rm{g}}}} \right)-\nabla \cdot \left({R{\rho _{\rm{w}}}{v_{\rm{w}}}} \right) + {q_{\rm{g}}} + {\tau _{{\rm{gsf}}}}=\frac{{\partial \left({\varphi {\rho _{\rm{g}}}{s_{\rm{g}}}} \right)}}{{\partial \tau }} + \frac{{\partial \left({\varphi R{\rho _{\rm{w}}}{s_{\rm{w}}}} \right)}}{{\partial \tau }}, $ | (1) |
| $-\nabla \cdot \left({{\rho _{\rm{w}}}{v_{\rm{w}}}} \right) + {q_{\rm{w}}} + {\tau _{{\rm{wsf}}}}=\frac{{\partial \left({\varphi {\rho _{\rm{g}}}{S_{\rm{w}}}} \right)}}{{\partial \tau }}. $ | (2) |
基质系统
| $-{\tau _{{\rm{wsf}}}}=\frac{\partial }{{\partial t}}\left({\frac{{{\varphi _{\rm{s}}}{S_{{\rm{ws}}}}}}{{{B_{{\rm{ws}}}}}}} \right), $ | (3) |
| $-{\tau _{{\rm{gsf}}}}=\frac{\partial }{{\partial t}}\left({\frac{{{\varphi _{\rm{s}}}{S_{{\rm{gs}}}}}}{{{B_{{\rm{gs}}}}}} + \frac{{{\varphi _{\rm{s}}}{R_{\rm{s}}}{S_{{\rm{ws}}}}}}{{{B_{{\rm{ws}}}}}}} \right). $ | (4) |
式中:ρg、ρw为储层压力下气体、水的密度,kg/m3;$ {\vec v_{\rm{g}}} $、$ {\vec v_{\rm{w}}} $为气、水相在储层中的渗流速度,m/s;Sg、Sw为储层含气、含水饱和度;Sgs、Sws为储层基质内的含气、含水饱和度;qg、qw为裂缝微元体内气体、水的注采量,注入为正,采出为负,kg/(m3·s);R、Rs为裂缝和基质内CO2气体的溶解气水比;φ、φs为储层内裂缝、基质孔隙度;τgsf、τwsf为基质与裂缝间气相、水相流体交换量,kg/(m3·s);Bg、Bw、Bgs、Bws为体积系数.
2)运动方程
由于气水两相渗流流动只存在于裂缝系统内,且流体在低渗储层内的流动存在启动压力梯度,故考虑启动压力梯度和重力作用影响的运动方程为
| $ {\vec v_{\rm{g}}}=-\frac{{K{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}\left({\nabla {p_{\rm{g}}}-\lambda-{\gamma _{\rm{g}}}\nabla D} \right), $ | (5) |
| $ {\vec v_{\rm{w}}}=-\frac{{K{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}}}\left({\nabla {p_{\rm{w}}}-\lambda-{\gamma _{\rm{w}}}\nabla D} \right). $ | (6) |
式中:μg、μw为气、水相在储层中的动力黏度,Pa·s;K为储层的绝对渗透率,μm2;Krg、Krw为气相、水相的相对渗透率;λ为启动压力梯度,MPa/m;γg、γw为气体和水的容重,γ=ρg,N/m3;pg、pw为气相、水相流体在地层中的渗流压力,MPa;D为渗流基准面以下的储层深度,m.
3)控制方程
将双重孔隙介质内气水两相渗流的运动方程(5)、(6)代入裂缝系统的连续性方程(1)、(2)中,得到描述气体在低渗透储层裂缝系统中渗流的微分方程:
| $ \nabla \cdot \left({\frac{{K{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}{B_{\rm{w}}}}}\left({\nabla {p_{\rm{w}}}-\lambda-{\gamma _{\rm{w}}}\nabla D} \right)} \right) + {q_{\rm{w}}} + {\tau _{{\rm{wsf}}}}=\frac{\partial }{{\partial t}}\left({\frac{{\varphi {S_{\rm{w}}}}}{{{B_{\rm{w}}}}}} \right), $ | (7) |
| $ \begin{array}{l} \nabla \cdot \left( {\frac{{K{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}{B_{\rm{g}}}}}\left( {\nabla {p_{\rm{g}}} - \lambda - {\gamma _{\rm{g}}}\nabla D} \right)} \right) + {q_{\rm{g}}} + {\tau _{{\rm{gsf}}}} + \\ \nabla \cdot \frac{{RK{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}{B_{\rm{w}}}}}\left( {\nabla {p_{\rm{w}}} - \lambda - {\gamma _{\rm{w}}}\nabla D} \right) = \frac{\partial }{{\partial t}}\left( {\frac{{\varphi {S_{\rm{g}}}}}{{{B_{\rm{g}}}}} + \frac{{\varphi R{S_{\rm{w}}}}}{{{B_{\rm{w}}}}}} \right). \end{array} $ | (8) |
4)补充方程
低渗透储层双重介质模型中的流体交换量主要由基质与裂缝系统之间的压差产生,其计算公式为
| $ {\tau _{{\rm{wsf}}}}=\sigma \frac{{{\rho _{\rm{w}}}K{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}}}\left({{p_{\rm{w}}}-{p_{{\rm{ws}}}}} \right), $ | (9) |
| $ {\tau _{{\rm{gsf}}}}=\sigma \left[{\frac{{{\rho _{\rm{g}}}K{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}\left({{p_{\rm{g}}}-{p_{{\rm{gs}}}}} \right) + \frac{{{\rho _{\rm{w}}}{R_{\rm{s}}}K{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}}}\left({{p_{\rm{w}}}-{p_{{\rm{ws}}}}} \right)} \right]. $ | (10) |
式中σ为单位体积中裂缝和基岩接触面积的形状因子(m-2),采用Kazemi[17]的计算方法求取,即
| $ \sigma=4\left[{\frac{1}{{{L_x}}} + \frac{1}{{{L_y}}} + \frac{1}{{{L_z}}}} \right]. $ | (11) |
式中:pgs、pws为气相、水相流体在基质介质中的渗流压力,MPa;Lx、Ly、Lz为基质块在x、y、z方向上的尺寸,m.
饱和度分布的平衡方程表示为
| $ {S_{\rm{g}}}=\left\{ \begin{array}{l} 1-S_{{\rm{res}}}^{\rm{w}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < z \le h; \\ 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h < z \le H. \end{array} \right. $ | (12) |
| $ {S_{\rm{w}}}=\left\{ \begin{array}{l} 1-S_{{\rm{res}}}^{\rm{w}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < z \le h; \\ 1, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h < z \le H. \end{array} \right. $ | (13) |
毛管压力约束方程
| $ {P_{\rm{c}}}={P_{\rm{g}}}-{p_{\rm{w}}}=f\left({{S_{\rm{w}}}} \right), $ | (14) |
| $ {P_{{\rm{cs}}}}={P_{{\rm{gs}}}}-{p_{{\rm{ws}}}}=f\left({{S_{{\rm{ws}}}}} \right). $ | (15) |
式中:$ S_{{\rm{res}}}^{\rm{w}} $为双重介质储层中的残余水饱和度;H为储层厚度,m;pc为气相与水相之间的毛管压力,为饱和度的函数.
CO2在做储气库垫层气的地下储存时一般处于超临界状态,且在水中的饱和度随储层压力的变化呈正相关性.CO2在水中的溶解度采用Henry定律[18]求解.
| $ {f_c}={x_c} \cdot {H_c}. $ | (16) |
式中:xc为水中CO2的摩尔分数,即CO2在水中的溶解度;Hc为Henry系数;fc为CO2的逸度系数,其计算方法利用PR-HV模型[19]根据相关储层的实际测井数据进行计算.
上述方程(3)、(4)、(7)、(8)构成地下储气库气水两相渗流的耦合控制方程组,利用辅助方程(9)~(15),将方程组中的关联变量消去,则方程组中含有4个独立未知量,本方程组采用pg、pgs、Sw、Sws.结合储气库地下储层的初始条件和边界条件,就构成了在低渗透气藏改建储气库中基于双重孔隙介质模型的描述气水两相流体渗流过程的控制方程组.方程中物性参数Bw、μw、γw、R等系数,由于受CO2在水中溶解度的影响,计算过程非常复杂,故文中计算时,当地层水饱和时,水相系数仅考虑为储层压力的函数;当地层水不饱和时,水相系数考虑为储层压力和饱和压力的二元函数,使用饱和压力ps代替水相饱和度.
在低渗透储层中,初始时刻的压力和饱和度为一已知函数,则初始条件为
| $ p\left({x, y, z, 0} \right)=\Phi \left({x, y, z} \right), $ | (17) |
| $ {S_{\rm{g}}}={S_{{\rm{g0}}}}\left({x, y, z} \right). $ | (18) |
储气库地下储层内的压力梯度为
| $ {\rm{d}}p{\rm{/d}}h{\rm{=const}}{\rm{.}} $ | (19) |
在低渗储层的气水边界处为第一类边界条件
| $ p\left| {_{{\Gamma _1}}} \right.={f_p}\left({x, y, z, t} \right). $ | (20) |
而在储气库的注采井井口处为第二类边界条件
| $ \frac{{\partial p}}{{\partial n}}\left| {_{{\Gamma _2}}} \right.={f_q}\left({x, y, z, t} \right). $ | (21) |
其中n表示法线方向.
1.2 控制方程组求解采用有线差分法对上述控制方程进行离散,并采用油气藏工程中常用的半隐式半显式IMPES方法[20~21]进行线性化,即压力隐式、饱和度显式的线性化方法.得到描述低渗气藏储层气水两相渗流过程的裂缝和基质孔隙系统中压力和饱和度的线性控制方程组.
裂缝系统
| $ \Delta W\Delta p_{\rm{g}}^{{\rm{n}} + 1}={F_1} + {F_2}-{\beta _1}P_{\rm{g}}^{\rm{n}}. $ | (22) |
式中:$ \begin{array}{l} \Delta W = B_{\rm{g}}^{\rm{n}}\Delta T_{\rm{w}}^{\rm{n}} + B_{\rm{w}}^{\rm{n}}\Delta T_{\rm{w}}^{\rm{n}},\\ {\beta _1} = \frac{{V{\varphi ^n}}}{{\nabla t}}\left[ {{C_{\rm{f}}} + {C_{\rm{g}}}{{\left( {1 - {S_{\rm{w}}}} \right)}^n} + {C_{\rm{w}}}S_{\rm{w}}^n} \right],\\ {F_1} = \frac{{RVB_{\rm{g}}^{n + 1}}}{{\Delta t}}\left[ {{{\left( {\frac{{\varphi {S_{\rm{w}}}}}{{{B_{\rm{w}}}}}} \right)}^n} - {{\left( {\frac{{\varphi {S_{\rm{w}}}}}{{{B_{\rm{w}}}}}} \right)}^{n - 1}}} \right],\\ \begin{array}{*{20}{l}} {{F_2} = \left( {B_{\rm{g}}^nA_{\rm{g}}^n + B_{\rm{w}}^nA_{\rm{w}}^n + RB_{\rm{g}}^nA_{\rm{w}}^n} \right) + \left( {B_{\rm{w}}^n + RB_{\rm{g}}^n} \right)\Delta T_{\rm{w}}^n\Delta p_{\rm{c}}^n - }\\ {\left( {B_{\rm{g}}^n{q_{\rm{g}}}V + B_{\rm{w}}^n{q_{\rm{w}}}V + B_{\rm{g}}^n{\tau _{{\rm{gst}}}}V + B_{\rm{w}}^n{\tau _{{\rm{wst}}}}V} \right).} \end{array} \end{array} $
基质系统
| $ {\beta _2}p_{{\rm{gs}}}^{n + 1}={F_3} + {\beta _2}p_{{\rm{gs}}}^n, $ | (23) |
| $ S_{\rm{w}}^{n + 1}=S_{\rm{w}}^n\frac{{{\varphi ^n}{B^{n + 1}}}}{{{\varphi ^{n + 1}}{B^n}}} + \frac{{\Delta t{B^{n + 1}}}}{{{V_{i, j, k}}{\varphi ^{n + 1}}}}\left[{\Delta {T_{\rm{w}}}\Delta p_{\rm{g}}^{n + 1}-\Delta {T_{\rm{w}}}\Delta {p_{\rm{c}}}\left({{S_{\rm{w}}}} \right)-A_{\rm{w}}^n + {q_{\rm{w}}}V + {\tau _{{\rm{wsf}}}}V} \right]. $ | (24) |
式中: $ \begin{array}{l} {\beta _2} = \frac{{\varphi _{\rm{s}}^n}}{{\Delta t}}\left[ {{C_{\rm{f}}} + {C_{{\rm{gs}}}}{{\left( {1 - {S_{{\rm{ws}}}}} \right)}^n} + {C_{{\rm{ws}}}}S_{{\rm{ws}}}^n} \right],\\ {F_3} = \frac{{RB_g^{n + 1}}}{{\Delta t}}\left[ {{{\left( {\frac{{{\varphi _s}{S_{{\rm{ws}}}}}}{{{B_{{\rm{ws}}}}}}} \right)}^n} - {{\left( {\frac{{{\varphi _s}{S_{{\rm{ws}}}}}}{{{B_{{\rm{ws}}}}}}} \right)}^{n - 1}}} \right] + B_{\rm{g}}^n{\tau _{{\rm{gsf}}}} + B_{\rm{w}}^n{\tau _{{\rm{wsf}}}}. \end{array} $
采用逐次点松弛迭代法(PSOR)[22]对离散出的储层内压力场的线性方程组进行MATLAB编程求解,计算得出储层内的压力分布后,代入相应的饱和度显示公式,求出相应时刻的饱和度场.在MATLAB编程求解的计算过程中,为了防止饱和度的误差较大,提高计算精度,采取多步求解法,即在求出n+1节点处的压力之后,计算该节点的饱和度时,将时间步长分成若干段,即$ \Delta {t^n} = \Delta t_1^n + \Delta t_2^n + \cdots + \Delta t_m^n, $由式(24)分别逐次计算出$ \Delta t_k^n $时刻的显式饱和度$ S_{wi,j,k}^k $后,且计算过程中,计算后一分段的$ S_{wi,j,k}^k $时,需要更新物性参数的系数矩阵,每次计算均采用新的系数矩阵代入式(24)计算求解,直到计算出$ \Delta t_m^n $为止,最终求出$ \Delta t_{k + 1}^n $时刻的饱和度.
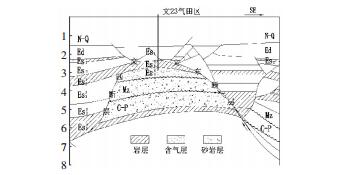
2 注CO2驱水的气水边界控制中原油田文23气藏由于边水侵入、气井出水等原因已于2008年底停止开采,2013年获批逐渐改建为低渗透气藏型地下储气库[23].图 2为该气田区域储层的纵向剖面示意图,图 3为改建储气库的$ Es_4^4 $储层部分井位布置图.该储气库建成后设计最大库容量为104.21×108 m3,有效设计工作气量46.23×108m3,日调峰能力3 800×104 m3/d[24].储层的其他物性参数如表 1所示.
|
图 2 文23气藏改建储气库的储层纵向剖面图 Figure 2 Vertical section of Wen-23 reconstructed gas storage by gas reserve |
| 表 1 储层的物性参数值 Table 1 Values of reservoir physical property |
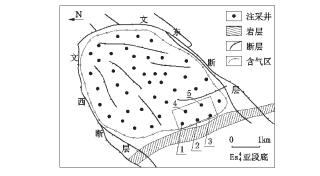
在储层边缘处选取5口注采井(如图 3所示),模拟采用不同注气方式在边缘井注CO2驱水扩容时储层内压力场和气水界面运移情况,单井注气量为50×104 m3/d,模拟区域注气区域面积为1.0 km×0.6 km,储层的具体计算网格步长为Δx=Δy=20 m、Δz=5 m;注采井附近的加密网格步长为Δx=Δy=5 m、Δz=2 m.5口注采井不同位置处的地层参数如表 2所示.
|
图 3 $ Es_4^4 $储层的含气构造与部分井位布置 Figure 3 Part of wells arrangement and gas structure map of $ Es_4^4 $ reservoirs |
| 表 2 文23气藏改建储气库不同气井处的储层参数 Table 2 Reservoir parameter at different gas well of Wen-23 reconstructed gas storage by gas reserve |
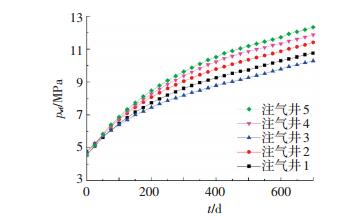
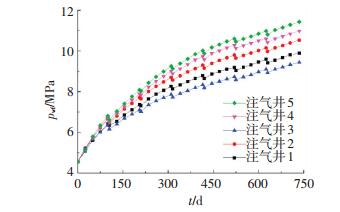
连续注气驱水扩容是指在地下储气库扩容建设的注气阶段采用连续性注气,向外驱边水扩容的方式.图 4为储气库扩容建库过程中,在边缘气井连续注入CO2时,井底流压随时间的变化.可以看出,在注气初期,井底流压的增速较大,随着注气的进行,井底流压的增速逐渐降低;连续注气700 d后,井5附近的井底流压最大,为12.62 MPa,而井3附近的井底流压最小,仅为10.49 MPa.这是由于不同气井处储层的渗透率不同造成的.结合表 2分析,由于井5附近储层的平均渗透率最小,附近储层的渗流速度也最慢,CO2在注气井附近集聚时间较长.而井3附近储层的渗透率较大且更加靠近气水边界,注入的CO2能够快速向外驱边水渗流,达到储气库快速扩容的目的.
|
图 4 连续注气时井底流压随时间变化 Figure 4 Curves of flowing bottomhole pressure (FBHP) over time when continuously gas injection |
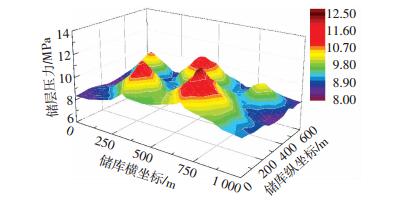
图 5为连续注气结束后计算区域内储层的压力分布.可以看出,连续注气700 d后,储层内的压力变化较大且分布不均.储层内压力极大值出现在各注气井附近,且计算区域最大储层压力在井5处为12.62 MPa,最小储层压力在井3附近的气水边界处,仅为8.13 MPa,区域储层内压差为4.49 MPa.结合图 4可知,离气水边界更近的注气井附近的储层压力增速较小,这也正符合储气库稳定和气水边界稳定运移的特性.
|
图 5 连续注气700 d后气水边界附近的储层压力场 Figure 5 Reservoir pressure field near the gas water boundary after continuously gas injection 700 days |
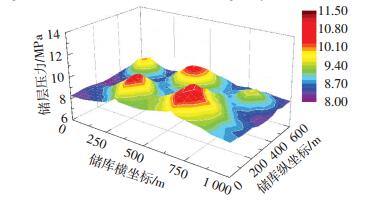
间歇注气驱水扩容是指在地下储气库扩容建设的注气阶段采用间断性注气方式向外驱水扩容.图 6为储气库间歇注CO2扩容时,井底流压随时间的变化.图 7为储气库间歇注气结束后计算区域储层的压力分布.分析两图可知,采用间歇注气的方式进行储气库扩容,井底流压升高较慢,累计注气700 d后(总工作时间为730 d),井5附近的井底流压最大为11.42 MPa,井3附近的井底流压最小为9.43 MPa,与连续注气扩容方式相比,其压力降幅分别为9.5 %和10.1 %.间歇注气结束后,储层压力分布更为平稳均匀,区域最大储层压力在井5处为11.42 MPa;而最小储层压力在井3附近的气水边界处为8.44 MPa,储层压差仅为2.98 MPa.由此可知,为了保证储气库的扩容速度,在无法大幅度降低注气速率的条件下,间歇性注气扩容方式能很好地抑制储层内压力增加过快、改善储层内压力分布不均现象,有利于储气库气水界面的安全稳定运移,保证储气库的快速扩容.
|
图 6 间歇注气时井底流压随时间变化 Figure 6 Curves of FBHP over time when gas injection at intervals |
|
图 7 间歇注气累积700 d后气水边界附近储层的压力场 Figure 7 Reservoir pressure field near the gas water boundary after gas injection at intervals up to 700 days |
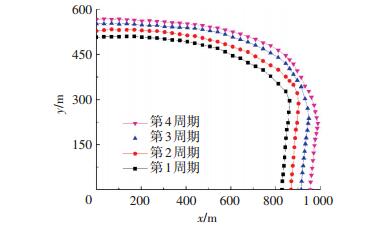
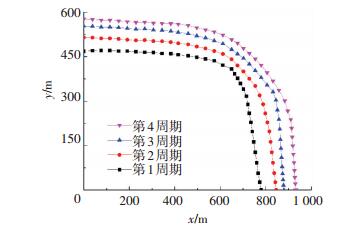
地下储气库的扩容建库过程是伴随着城市调峰相继进行的,即在未达到设计库容时,以扩容为主要目的,调峰时采用多注少采的方式进行.图 8和图 9分别为在储气库扩容的注气阶段,连续注气和间歇注气时的气水边界运移情况.每个注采扩容周期中,注气阶段260 d,采气阶段90 d,注采气结束后分别关井5 d.其中间歇注CO2垫层气的方式采用注气50 d关边缘井2 d的方式.分析两图可知:随着扩容周期的增多,间歇注气扩容的气水边界运移更加稳定.4个扩容注气结束后,连续注气扩容的含气区域面积为0.499 km2,间歇注气扩容的含气区域面积也达0.475 km2,扩容速度仅降低4.8 %.然而,连续注气扩容的气水边界注气井3附近有一定的突进现象,间歇注气扩容的气水边界更平稳,增大了地下储层扩容的安全性.
|
图 8 连续注气时气水边界运移 Figure 8 Migration of gas-water boundary when continuously gas injection |
|
图 9 间歇注气时气水边界运移 Figure 9 Migration of gas-water boundary when gas injection at intervals |
储气库在扩容建库过程结束后进入季节性的城市调峰阶段.在储气库城市调峰阶段,CO2作为垫层气稳定地储存在储层外围区域.图 10为储气库在稳定运行50 a的季节性城市调峰运行阶段,储层内CO2储量随时间的变化.可以看出,CO2在储气库内主要以超临界态和溶解态两种形式存在.CO2在水中溶解度随储层压力增大而增大,在储气库进行调峰采气阶段,由于储层压力降低引起的溶解度降低导致部分溶解态CO2释放为超临界态,更好地维持了储层内的压力;在调峰注气储存阶段,部分CO2溶于边水释放一定的储层空间用来存储更多的天然气,增大了储层空间的有效利用率.同时,CO2在水中的这一溶解特性在储气库的气水边界处起到了良好的调节作用,很好地稳定了储气库的工作区域.

|
图 10 储气库稳定运行50 a期间CO2储量变化 Figure 10 Curves of CO2 reserves over time during stable operation 50 a of USG |
分析图 10可知,在城市调峰的多周期注采过程中,超临界态CO2有一定幅度减少,溶解态CO2则逐渐增多,CO2总量也小幅度减少,主要因为部分CO2在水中钙化沉积,另外,少量CO2垫层气会沿盖层裂缝、断层或边缘气井等方式逃逸或渗流流失.因此,在储气库的扩容建库和季节性城市调峰的稳定运行阶段均应实时监测含气区域储层的工作状态,以防气体逃逸或者边水侵入.
图 11为储气库稳定调峰运行50 a后,储气库某一采气调峰阶段结束后气水边界附近储层内的压力分布.可以看出,储气库经过多周期的城市调峰和稳定储存后,计算区域内储层压力分布逐渐平缓,储层内压力的极大值出现在边缘观察井附近,此时计算区域内储层的最大压差仅为1.69 MPa,比建库扩容阶段计算区域内的储层压差明显降低,这样更加有利于储气库进行稳定的城市调峰.

|
图 11 储气库稳定运行50 a后气水边界附近储层的压力场 Figure 11 Reservoir pressure field near the gas water boundary after stable operation 50 a of UGS |
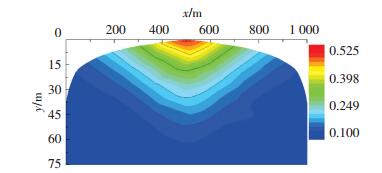
图 12为储气库季节调峰周期内某一采气阶段结束后气水边界附近垫层气区CO2的浓度分布.可以看出,垫层气区域内CO2浓度峰值出现在井2附近,这是由于此处储层厚度较大且井深较浅,形成小范围内CO2集聚气顶,而在其余垫层气区域,CO2均能够稳定地储存在含气储层的边缘,起到储气库垫层与隔离边水的作用.
|
图 12 储气库稳定运行50 a后CO2纵向的饱和度分布 Figure 12 Longitudinal saturation distributions of CO2 after stable operation 50 a of UGS |
1)基于低渗透地下储层中注CO2驱水的气水运移特性,建立了低渗透储层孔隙-裂缝的双重孔隙介质模型,并以中原油田文23气藏改建储气库的地下储层为研究对象,讨论扩容建库时CO2垫层气的注入方式对储气库扩容速率和气水边界的影响和季节调峰时气水界面的运移规律.
2)扩容建库阶段,连续性注CO2驱水扩容能快速地扩容、增大含气区域面积,同时造成气水边界附近储层压力梯度较大,气水界面运移的稳定性较差;间歇性注CO2驱水扩容虽然在一定程度上减缓了储气库的扩容速度,却能有效地降低气水边界附近的储层压力梯度,大大提高气水界面运移的稳定性.故在储气库注气驱水扩容建库时,应更多地采用间歇性注CO2驱水扩容的建库方式.
3)季节调峰阶段,注气时部分超临界态CO2溶于边水,释放出更多的储层空间存储天然气,增大储层空间的利用率;采气时由于压力降低,部分溶解态CO2释放为超临界状态而增大垫层气量,维持储层工作压力,很好地保持气水边界的稳定.地下储气库经过多周期的季节性注采调峰后,垫层气区储层压力场更加稳定,饱和度分布也更加平稳,大大增加了储气库调峰运行的稳定性和安全性.
| [1] |
潘勋章, 滕飞, 王革华. 不同碳排放权分配方案下各国减排成本的比较[J].
中国人口·资源与环境,2013, 23 (12) : 16-21.
PAN Xunzhang, TENG Fei, WANG Gehua. Comparative study of countries' abatement costs under different carbon emission rights allocation schemes[J]. China Population, Resources and Environment,2013, 23 (12) : 16-21. (  0) 0)
|
| [2] |
WANG Zheng, ZHU Yongbin, PENG Yongming. Carbon emissions trends with optimal balanced economic growth of China and the USA and some abatement options for China[J].
Journal of Geographical Sciences,2013, 23 (6) : 991-1004.
DOI: 10.1007/s11442-013-1058-y ( 0) 0)
|
| [3] |
SINGH A K, GOERKE U J, KOLDITZ O. Numerical simulation of non-isothermal compositional gas flow: application to carbon dioxide injection into gas reservoirs[J].
Energy,2011, 36 (5) : 3446-3458.
DOI: 10.1016/j.energy.2011.03.049 ( 0) 0)
|
| [4] |
魏欢, 田静, 李建中, 等. 中国天然气地下储气库现状及发展趋势[J].
国际石油经济,2015, 23 (6) : 57-62.
WEI Huan, TIAN Jing, LI Jianzhong, et al. Status and development trend of China underground natural gas storages[J]. International Petroleum Economics,2015, 23 (6) : 57-62. (  0) 0)
|
| [5] |
李伟, 陈燕, 粟科华, 等. "十三五"期间我国天然气行业发展环境分析[J].
国际石油经济,2015, 23 (3) : 5-10.
LI Wei, CHEN Yan, SU Kehua, et al. China's natural gas industry during the 13th five-year plan[J]. International Petroleum Economics,2015, 23 (3) : 5-10. (  0) 0)
|
| [6] |
EVANS D J, CHADWICK R A. Underground gas storage: worldwide experiences and future development in the UK and Europe[J].
Geological Society, London, Special Publications,2009, 313 (1) : 25-37.
DOI: 10.1144/SP313.4 ( 0) 0)
|
| [7] |
林涛.二氧化碳做储气库垫层气注采动态模拟及优化运行控制[D].哈尔滨:哈尔滨工业大学, 2008.
LIN Tao.Simulation of injection-production and optimization of running control in gas reservoirs using carbon dioxide [D]. Harbin: Harbin Institute of Technology, 2008. (  0) 0)
|
| [8] |
丁国生, 王皆明. 枯竭气藏改建储气库需要关注的几个关键问题[J].
天然气工业,2011, 31 (5) : 87-89.
DING Guosheng, WANG Jieming. Key points in the reconstruction of an underground gas storage based on a depleted gas reservoir[J]. Natural Gas Industry,2011, 31 (5) : 87-89. (  0) 0)
|
| [9] |
RIOS R B, BASTOS-NETO M, AMORA M R, et al. Experimental analysis of the efficiency on charge/discharge cycles in natural gas storage by adsorption[J].
Fuel,2011, 90 (1) : 113-119.
DOI: 10.1016/j.fuel.2010.07.039 ( 0) 0)
|
| [10] |
王东旭, 马小明, 伍勇, 等. 气藏型地下储气库的库存量曲线特征与达容规律[J].
天然气工业,2015, 35 (1) : 115-119.
WANG Dongxu, MA Xiaoming, WU Yong, et al. Curve characteristics and rules of the storage capacity establishment of a reservoir-type underground gas storage (UGS)[J]. Natural Gas Industry,2015, 35 (1) : 115-119. (  0) 0)
|
| [11] |
谭羽非, 展长虹, 曹琳, 等. 用CO2作垫层气的混气机理及运行控制的可行性[J].
天然气工业,2005, 25 (12) : 105-107.
TAN Yufei, ZHAN Changhong, CAO Lin, et al. Gas mixing mechanism taking CO2 as cushion gas and feasibility of operation control[J]. Natural Gas Industry,2005, 25 (12) : 105-107. (  0) 0)
|
| [12] |
谭羽非, 林涛. 凝析气藏地下储气库单井注采能力分析[J].
油气储运,2008, 27 (3) : 27-29.
TAN Yufei, LIN Tao. Analysis on the single-well capacity of injection/withdrawal in underground gas storage reservoir[J]. Oil & Gas Storage and Transportation,2008, 27 (3) : 27-29. (  0) 0)
|
| [13] |
CAO Lin, TAN Yufei. Dynamic simulation research on injection and withdrawal performance of underground salt cavern natural gas storage[J].
Journal of Harbin Institute of Technology (New Series),2009, 16 (5) : 633-637.
( 0) 0)
|
| [14] |
NIU Chuankai, TAN Yufei, FENG Liyan. Stability analysis of multi-well gas injection for storing CO2 in underground aquifer[J].
Advanced Materials Research,2014, 869/870 : 803-807.
( 0) 0)
|
| [15] |
NIU Chuankai, TAN Yufei. Numerical simulation and analysis of migration law of gas mixture using carbon dioxide as cushion gas in underground gas storage reservoir[J].
Journal of Harbin Institute of Technology (New Series),2014, 21 (3) : 121-128.
( 0) 0)
|
| [16] |
GELET R, LORET B, KHALILI N. Borehole stability analysis in athermoporoelastic dual-porosity medium[J].
International Journal of Rock Mechanics and Mining Sciences,2012, 50 (2) : 65-76.
( 0) 0)
|
| [17] |
KAZEMI H, PORTERFIELD K L, ZEMAN P R. Numerical simulation of water-oil flow in naturally fractured reservoirs[J].
Society of Petroleum Engineers Journal,1976, 16 (6) : 317-326.
DOI: 10.2118/5719-PA ( 0) 0)
|
| [18] |
侯大力, 罗平亚, 王长权, 等. 高温高压下CO2在水中溶解度实验及理论模型[J].
吉林大学学报(地球科学版),2015, 45 (2) : 564-572.
HOU Dali, LUO Pingya, WANG Changquan, et al. Experimental research and theoretical model for CO2 solubility in water under high temperature and high pressure[J]. Journal of Jilin University(Earth Science Edition),2015, 45 (2) : 564-572. (  0) 0)
|
| [19] |
SECUIANU C, FEROIU V, GEANA D. Phaseequilibria calculations for carbon dioxide plus methanol binary mixture with the Huron-Vidal infinite dilution (HVID) mixing rules[J].
Revista De Chimie,2009, 60 (5) : 472-475.
( 0) 0)
|
| [20] |
KOU Jisheng, SUN Shuyu. A new treatment of capillarity to improve the stability of IMPES two-phase flow formulation[J].
Computers & Fluids,2010, 39 (10) : 1923-1931.
( 0) 0)
|
| [21] |
MONTEAGUDO J E P, FIROOZABADI A. Comparison of fully implicit and IMPES formulations for simulation of water injection in fractured andunfractured media[J].
International Journal for Numerical Methods in Engineering,2007, 64 (4) : 698-728.
( 0) 0)
|
| [22] |
NAJAFI H S, EDALATPANAH S A. On the modified symmetricsuccessive over-relaxation method for augmented systems[J].
Computational and Applied Mathematics,2015, 34 (2) : 607-617.
DOI: 10.1007/s40314-014-0127-x ( 0) 0)
|
| [23] |
李铮.中原油田文23战略储气库项目获批[N].河南日报, 2013-10-17(4).
LI Zheng. The project has been approved of Wen-23 strategy of gas storage in Zhongyuan Oilfield [N]. Henan Daily, 2013-10-17(4). (  0) 0)
|
| [24] |
何晓云, 何晓娜, 周延芳, 等. 《气藏开发调整方案编制技术要求》在文23气田中的实施与应用[J].
内蒙古石油化工,2010, 36 (11) : 48-49.
HE Xiaoyun, HE Xiaona ZHOU Yanfang, et al. The implement and application of "Technical requirements for preparing of development plan adjustment for gas reservoir"in Wen-23 gas field[J]. Inner Mongolia Petrochemical Industry,2010, 36 (11) : 48-49. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


