2. 哈尔滨工业大学(威海) 计算机科学与技术学院,山东 威海 264209
2. School of Computer Science and Technology, Harbin Institute of Technology at Weihai, Weihai 264209, Shandong, China
在软件发布前的测试阶段以及之后的运行阶段,软件可靠性增长模型SRGM(software reliability growth model)是用来定量建模可靠性增长过程的重要数学工具[1-3],已获得了广泛应用.SRGM采用基于随机过程理论的数学微分方程(组)来描述故障检测与移除过程[4-6],使得与可靠性R(t)直接依赖的参变量被求解出来,进而为可靠性的提高与评测,测试资源分配以及最优发布提供决策依据.目前,已有数百个SRGMs被提出,其建模过程类别存有较大差异,且均在有限个数的失效数据集上表现出良好的性能[7-9],但这些模型隐藏的内在本质差异在当前研究中却鲜有提及.本文探讨与挖掘差异的根源有助于洞悉SRGM在建模描述测试过程的本质,也为提出性能更优的模型和在实际工程中选择SRGMs提供必要的科学依据.
1 NHPP类SRGM建模基础与发展历程 1.1 NHPP类SRGM建模基础假设及可靠性增长含义现有的上百个SRGM建立了失效检测/改正个数与执行时间之间的对应关系,可以分为[10]:指数型和S型模型.指数型模型以Geol-Okumoto模型(记为G-O)[9]及其改进为代表; S型模型以Yamada模型[11]为代表.这些非齐次泊松过程NHPP(non-homogeneous poisson process)类SRGMs的建立均是基于以下公共基础假设[1, 6, 9, 11-15],并在此基础上进行更为靠近实际测试过程的假设.
1)软件失效随机发生,失效观察与故障移除满足非齐次泊松过程NHPP.
2)定义随机计数过程[N(t), t≥0].其中N(t)表示到[0, t]内累计检测到故障数量,其均值函数为m(t),m(0)=0,基于NHPP基本性质可得
| $ \Pr \left[ {N\left(t \right)=N} \right]=\frac{{\left[ {m{{\left(t \right)}^n}} \right]' \times {{\rm{e}}^{-m\left(t \right)}}}}{{n!}}, \left({n=0, 1, 2, ...} \right). $ |
| $ \lambda \left( t \right) = \frac{{{\rm{d}}m\left( t \right)}}{{{\rm{d}}t}}.$ |
这里,假定上次失效的时间为t(t≥0, x>0),则在(t, t+x]内可靠性如下.显然,R(x|t)与m(t)紧密关联,因而现有SRGM研究的核心是如何找到最适宜的m(t)函数,使得R(x|t)能够得到有效提高.
| $ R\left({\left. x \right|t} \right)={{\rm{e}}^{-\left({m\left({t + x} \right)-m\left(t \right)} \right)}}. $ |
设T为软件发布时间,运行阶段的可靠性表示为
| $ R\left({\left. x \right|T} \right)={{\rm{e}}^{-l\left(T \right)x}}. $ |
基于上述分析,可以认为,SRGM基于失效数据描述软件测试过程中累积检测的故障数量,TE与测试时间等的数学关系[14, 16],是实现建模软件可靠性提高过程的数学工具.
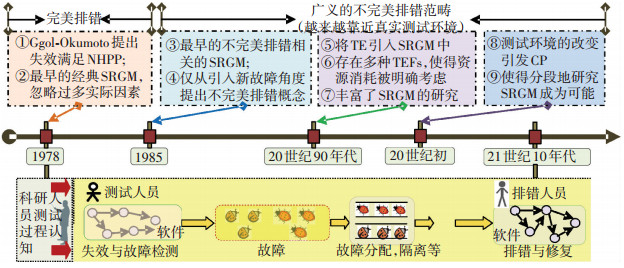
1.2 SRGM发展演变概要分析不同SRGMs的建模假设在上述基础上,依据对测试过程的认知,又进行了不同的假设,使得建立的SRGMs差异较大.以G-O模型为起点,SRGM发展经历了如图 1所示的历程.
|
图 1 近40年来SRGM发展历程 Figure 1 Development history of SRGM in the past 40 years |
从1970年开始,SRGMs逐渐得到了广泛的研究.早在1978年,文献[9]使用一个NHPP作为随机过程来描述失效过程,后来文献[11]修改了G-O模型并将TE引入到NHPP模型中获得了更好的效果.SRGMs通常基于失效数据[12](失效个数\失效时间\TE\失效严重程度或连续失效的时间间隔)来建立软件测试过程的数学关系描述模型.因而,随着研究人员对测试过程认知的深入,SRGM正在将真实测试环境(例如,不完美排错[17-20])融入建模中.
2 两类基本SRGM:指数型与S型本文从相对统一的建模角度[10]来分析两类SRGMs建模流程与关联.在建模基础上,增加如下假设:1)引起失效发生的故障立即被排除,无新故障引入;2)(t, t+Δt)内累积检测到的故障数量与当前软件中剩余的故障数量成正比;3)故障检测率与当前剩余故障数量成正比,且该比例随着故障排除而线性增加;4)软件中存在相互独立与依赖的两种类型故障.
基于上述假设,可以得到以下微分方程
| $ \frac{{{\rm{d}}m\left(t \right)}}{{{\rm{d}}t}}=f\left(t \right)\left({a-m\left(t \right)} \right), $ |
其中
| $ \varphi \left(t \right)=b\left({r + \left({1-r} \right)\frac{{m\left(t \right)}}{a}} \right) $ |
式中:a为测试之初故障总数;b为常量;φ(t)为时间相关的故障检测率,由于这里认为被检测到的故障立即被排除,因此也被称为故障移除率;r为弯曲参数,用以描述独立不相关故障比例.在t=0,m(t)=0的初始条件下求解可得到
| $ m\left(t \right)=a\left({\frac{{1-{{\rm{e}}^{-bt}}}}{{1 + \left({\left({1-r} \right)/r} \right){{\rm{e}}^{-bt}}}}} \right). $ | (1) |
当r=1时,式(1)可变为
| $ m\left(t \right)=a\left({1-{{\rm{e}}^{-bt}}} \right), $ | (2) |
此为文献[9]提出的经典的G-O模型.因其m(t)曲线呈现指数性增长趋势,被称为指数性模型,同时也被叫做Musa模型.
当令$ \beta=\frac{{\left({1-r} \right)}}{r} $时,式(1)可变为
| $ m\left( t \right) = a\left( {\frac{{1 - {{\rm{e}}^{ - bt}}}}{{1 + \beta {{\rm{e}}^{ - bt}}}}} \right), $ |
此为Inflection-S型SRGM[21].显然若β=0,则该S型模型又转化为指数型的G-O模型.另一种典型的S型模型是延迟型,是G-O模型的一种改进,其形式为
| $ m\left(t \right)=a\left({1-\left({1 + bt} \right){{\rm{e}}^{-bt}}} \right). $ |
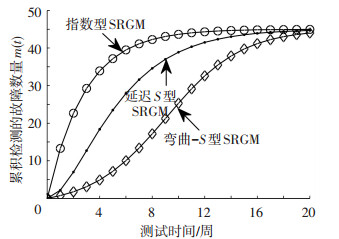
图 2给出了两类SRGM的基本形状,其中设定a=45, r=0.04, b=0.35, t∈[0, 20]仅用以展示曲线形状.
|
图 2 两类基本的SRGMs:指数型与S型 Figure 2 Two typical SRGMS: exponential and S type |
实际的测试过程中含有大量的随机因素,因而从获取更为准确的SRGM角度出发,试图兼顾到更多真实情况的不完美排错相关的SRGM一直是研究人员关注的重点.此外,软件测试与成本紧密相关,易知融入测试工作量TE[22]到SRGM中是一个重要研究分支.
3.1 不完美排错相关的SRGM本文以经典的不完美排错SRGM模型:Pham模型[8]为示例进行阐释.Pham模型建立的微分方程为
| $ \frac{{{\rm{d}}m\left(t \right)}}{{{\rm{d}}t}}=b\left(t \right) \times \left[ {a\left(t \right)-m\left(t \right)} \right], $ | (3) |
该微分方程所做的假设为:[0, t]内累积检测到的故障个数m(t)与剩余的故障个数[a(t)-m(t)]成比例,比例函数为b(t).同时,文献[7]认为,a(t)=a(1+rt),即a(t)是测试时间t的线性增函数,这表明测试中会引入新故障,因而被称为不完美排错模型;b(t)是故障检测率,设定$ b\left(t \right)=\frac{{b\left({1 + \sigma } \right)}}{{1 + \sigma {{\rm{e}}^{-b\left({1 + \sigma } \right)t}}}}, $,σ是反映测试人员的学习因子.在m(0)=0, a(0)=0的初始条件下,可求解得到
| $ m\left(t \right)=\frac{a}{{1 + \sigma {e^{-b\left({1 + \sigma } \right)t}}}}\left[ {\left({1-{{\rm{e}}^{-b\left({1 + \sigma } \right)t}}} \right)\left({1-\frac{r}{{b\left({1 + \sigma } \right)}}} \right) + rt} \right]. $ |
验证的核心是将求解得到的m(t)与真实的失效个数进行比较[23-26].在比较内容上包括:拟合与预测.拟合是基于拟合标准计算m(t)与真实失效数据集之间的偏差,通常偏差值越小越好;预测是求解并画出预测曲线,曲线越快趋于0效果越好.其具体步骤为:1)基于失效数据集中不同时间点的累积故障数量对m(t)表达式中的参数进行估计:可以采用LSE(least squares method),MLE(maximum likelihood method)或者采用数值求解软件(例如Matlab, Labview, SPSS等)给出数值解;2)将参数估计结果代入m(t)中,求解出m(t)的表达式;3)将m(t)与真实的失效个数进行比较:拟合与预测;4)基于评价结果给出模型的优劣评价.
3.2 考虑TE时的SRGM建模故障检测与修复是在TE的消耗下进行的,因而SRGM中应考虑到TE的存在.这样,在式(3)的基础上,当考虑TE时,可以得到以下文献所采用的模型[1, 6, 10, 12-15]
| $ \frac{{{\rm{d}}m\left(t \right)}}{{{\rm{d}}t}} \times \frac{1}{{w\left(t \right)}}=b\left(t \right) \times \left[ {a-m\left(t \right)} \right], $ | (4) |
式中w(t)为测试工作量消耗率函数,满足$ w\left(t \right)=\frac{{{\rm{d}}W\left(t \right)}}{{{\rm{d}}t}} $,通常W(0)=0,但也存在W(0)≠0的情况[15],代表测试之初需要消耗部分测试资源做准备.这里主要关注w(t)的参与,这样在b(t)=b, m(0)=0的初始条件下,可求解得到
| $ m\left(t \right)=a\left[ {1-{{\rm{e}}^{-b\left({W\left(t \right)-W\left(0 \right)} \right)}}} \right], $ | (5) |
鉴于式(4)中考虑到了TE,因而使其能够将测试资源的影响纳入到SRGM中.当SRGM中考虑到TE时,其验证步骤为:1)基于TE数据,对W(t)中参数进行估计,本步骤估计中采用LSE[1]的方法较多;2)再对m(t)中剩余的参数进行估计;3)后续步骤与前述相一致.
4 SRGMs性能验证与分析 4.1 参与比较的模型、数据集及评价标准本文精心选择8个典型的不完美排错相关以及考虑到TE的SRGMs在数据集DS1~DS4[23-26]上来进行验证,见表 1.这些公开发表的4个数据集已被广泛用来作为分析SRGMs的性能.其中DS1和DS2记录有失效发生的时间和累计检测到的故障数量,用以验证模型①~⑤的性能;DS3和DS4还包括描述测试资源消耗的TE数据,用以验证模型⑥~⑧的性能.
| 表 1 参与比较的模型及建模过程 Table 1 The selected models for comparison and modeling process |
目前,对SRGM性能的验证,主要采用以下拟合与预测标准:MSE, MEOP, Variation, RMS-PE, TS和BMMRE越小,R-square越接近于1,这表明拟合效果越好;RE越快趋近于0表明预测效果越好.
4.2 结果与分析 4.2.1 不完美排错相关的SRGM性能评价首先,基于数据集DS1和DS2进行的参数估计,本文给出了不完美排错相关的5个模型,即模型①~⑤在DS1和DS2上的拟合效果图,如图 3所示.

|
图 3 模型①~⑤在DS1与DS2上的拟合结果 Figure 3 Comparison of goodness of fitting of the models①~⑤in DS1 and DS2 |
除模型③即P-Z-2以外的4个模型与真实的失效数据曲线拟合的均较好.可以看出此4个模型呈现出了与真实的失效数据曲线一样的凸形状,而模型③却呈现凹形状.造成该现象的原因是,虽然模型③的建模与其余4个模型在本质上相一致,但故障检测率b(t)与软件中总故障个数a(t)自行设定的结果使得求解得到的m(t)与真实失效数据曲线走向发生严重背离.
为了进一步区分其余4个模型的细微差异,本文计算了其在拟合标准上的具体数值,见表 2.
| 表 2 SRGM:模型①~⑤性能比较标准结果 Table 2 SRGM: performance comparison results for the models①~⑤ |
表 2中最好的指标采用下划线来表示,其次的指标用波浪线表示,再次的指标用双下划线表示,表 3、4中也采用同样方法.容易看出,模型④即P-Z-1模型在DS1和DS2上的拟合效果是最优的,仅在DS2上的R-square指标上是次优的,且与最好的指标相差在小数点后第3位上.模型④最优的原因可以解释为非降的弯曲S型故障检测率函数b(t),以及软件中总故障个数a(t)随时间基本满足指数增加的事实.次优的是模型⑤即Pham模型,其具有6个次优的指标;再次是模型①即G-O模型.而模型③即P-Z-2模型的指标是最差的,这与图 2中其曲线严重偏离真实的失效数据曲线相一致.
另外,虽然模型①G-O模型是最早提出的SRGM,是后续模型研究的根基,但由于其设定b(t)和a(t)为常量,造成一定误差出现,这使得其性能不如前者.在预测性能上,图 4给出了5个模型的RE曲线.
在图 4(a)描述DS1的预测曲线中,可以明显看出,模型④即P-Z-1最快地趋近于0,预测效果最好,其次是模型①即G-O,再次是模型⑤即Pham,模型②即P-N-Z仅比模型③强,而模型③在有限的测试时间内已经无法准确地表现出预测能力.整体而言,5个模型的性能依次为:④>①>⑤>②>③.在图 4(b)中,除模型③严重偏离0基准线外,其余4个模型在预测性能上基本相同,表现出了优异性能,这里不再进行区分.

|
图 4 模型①~⑤在DS1与DS2上的预测结果 Figure 4 Prediction results for the models①~⑤in DS1 and DS2 |
另外,图 4两幅图中均显示出自测试时间1/2开始,模型的预测性能开始逐渐收敛趋近于0,呈现增强的态势.这是由于,测试半程以后,已积累了适量的预测所需数据,测试环境与策略和技术开始变得稳定,这些使得模型的预期性能开始变好.
4.2.2 考虑TE的SRGM性能评价通常,含有TE的SRGM需要先基于实际消耗的TE数据进行计算,再对累积失效的故障数量m(t)进行评估.表 3给出了模型⑥~⑧中所采用的TEF在DS3和DS4上的性能比较.
| 表 3 SRGM:⑥~⑧模型中TE性能比较标准结果 Table 3 SRGM: TE performance comparison results for the models⑥~⑧ |
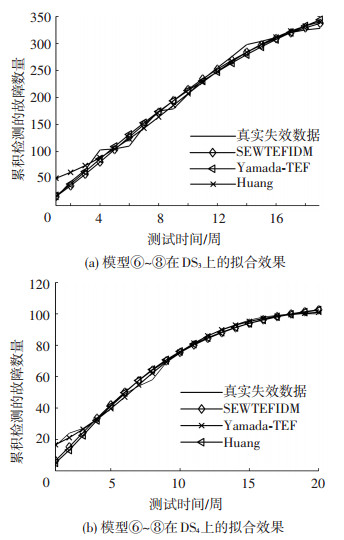
从表 3可以看出,模型⑦和⑧中所采用的Weibull(威布尔)和Exponentiated Weibull(指数威布尔)类型的TEF在DS3和DS4上表现得较好,这为接下来的m(t)性能评估贡献了积极的因素.图 5给出了模型⑥~⑧在失效数据方面的拟合效果.
从图 5直观上看,3个模型的m(t)与真实的失效数据曲线基本发生了重合,表明在DS3和DS4上拟合效果较好.表 4通过计算性能比较标准值用以明确分辨3个模型的细微差异性.
从表 4可以看出,在DS3上,模型⑧表现最优(7个标准中有5个最优,2个次优);模型⑦次之(7个标准中有2个最优,5个次优);而模型⑥则无最优和次优值,因而最差.在DS4上,出现了颠覆性的结果:模型⑥出现了7个最优的标准值,因而性能最优;模型⑧占据了全部7个标准值中的次优结果,这使得其性能为三者居中;而模型⑦则最差.
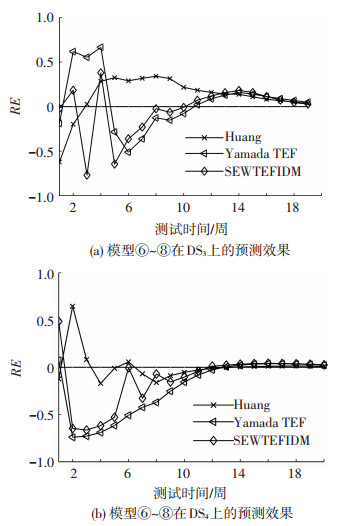
由表 1可看出,模型⑥、⑦和⑧在建模本质上相差不大,但所采用的TEF存有很大差异使得3个模型性能各异.另外模型⑧中的$ \varphi \left(t \right)=b\left[ {r + \left({1-r} \right)\frac{{m\left(t \right)}}{a}} \right] $因参数r的变动使得其能够适用多种情况,因而其在DS3和DS4上的整体表现尚可.图 6所显示出的预测性能曲线表明3个模型的预测能力均较好(这里不再进行严格区分),尤其从t=12开始,曲线开始向0标准收敛靠近.
|
图 5 模型⑥~⑧在DS3与DS4上的拟合结果 Figure 5 Comparison of goodness of fitting of the models⑥~⑧in DS3 and DS4 |
| 表 4 SRGM:⑥~⑧模型性能比较标准结果 Table 4 SRGM: performance comparison results for the models⑥~⑧ |
|
图 6 模型⑥~⑧在DS3与DS4上的预测结果 Figure 6 Prediction results for the models⑥~⑧in DS3 and DS4 |
1)特别指出,模型③即P-Z-2在DS1和DS2上表现得差强人意,但在某些数据集上却很优异,另一方面,这里表现优异的模型也存在于某些数据集上偏差较大.这说明一个模型不可能适应于所有的数据集.
2)另外,一个不容忽视的事实是,DS1的测试时间t是以数值较大的时钟时间为单位,与大部分失效数据集的以周为单位相迥异;DS1以累积失效个数为顺序记录,与绝大部分以失效时间为顺序记录累积失效个数方式也极为不同,这些综合因素使得其与模型③中m(t)表达式存有很严重的不匹配现象,因而造成模型③性能表现最差.当然,这种数据集在当前可收集到的数据集中并不多见,本文这里特用以说明该事实.
3)显然,对测试过程的深入认识以及由此建立考虑更多实际因素的数学模型,能够刻画更多的测试细节,但随着引发的求解难度也急剧增加.例如,当所建立的模型考虑到更多的细节,且存有一定的限制条件时,欲获得m(t)的表达式已经变得无法解析求解,此时只能采用非解析方法(借助于计算机利用数学求解软件来给出数值解,例如Matlab, Labview等),甚至在有些情况下只能给出上下界.
4)当考虑TE到SRGM中时,当前研究主要还是对m(t)的拟合与预测结果进行最终的评估.实际上,TE代表着测试成本的支出,虽然高可靠性是SRGM的本质要求,但追逐这一目标还需要兼顾到成本的花销.
4.3 SRGM性能差异化总体分析从上述8个模型在4个数据集上的实验结果与性能分析可以看出:
1)直观上,不同SRGMs的差异体现在所求解得到的m(t)上,但这种差异的根源缘由以下两点决定:①失效数据集是决定SRGMs差异的客观因素:不同公司、不同测试环境与策略,直接导致失效数据的收集、记录等存有不一致;②建模假设的内容是决定SRGMs差异的主观因素:从上述实验可以看出,即便基于同一失效数据集,研究人员做出的假设上的差异直接导致数学模型的不同.
2)SRGMs的性能强烈地依赖于数据集:例如,模型⑧模型在DS3上表现得优异,但在DS4上却不理想.
3)由于不同模型对测试认知过程中的差异,以及所建立的模型的差别,使得其在同一个数据集上的性能差异较大.
4)整体上,在数据集较大的情况下,拟合效果有效的SRGM,其在预测性能上也相对表现优秀:这是因为,拟合和预测在时间的选取上具有很强的相对性,可能存在交叉而造成的.
5)本文给出的8个模型在4个失效数据集上的结果表明并不存在一个模型能够适应所有的数据集.对于该事实的确立,本文对26个模型在可搜集到的15个失效数据集上的实验结果已表明.
5 结论1)由于不同公司在测试过程中存在测试环境、策略、技术以及数据收集等因素上的差异,使得不同失效数据集的差异较大,这为不同SRGMs的性能差异带来了客观上的解释.
2) SRGM是客观与主观结合下研究人员去建模描述不同失效数据集的过程,因而造成一个SRGM选择上的难题:能够准确拟合与预测所有失效数据集的SRGM并不存在,但在有限个数的数据集上,采用合适的评价标准是可以优选出相对最优的SRGM,这是近期SRGM研究的一个方向.
3) SRGM的本质即是提出能够更为准确地度量拟合过去的失效数据,同时又能准确地预测未来失效情况的数学模型.这样,考虑到更多真实的测试环境要素,建立全面的SRGM已成为当前研究中亟待解决的难题.
| [1] |
AHMAD N, BOKHARI M U, QUADRI S M K, et al. The exponentiated Weibull software reliability growth model with various testing-efforts and optimal release policy: a performance analysis[J].
International Journal of Quality & Reliability Management,2008, 25 (2) : 211-235.
DOI: 10.1108/02656710810846952 ( 0) 0)
|
| [2] |
DOHI T, MATSUOKA T, OSAKI S. An infinite server queuing model for assessment of the software reliability[J].
Electronics and Communications in Japan (Part III: Fundamental Electronic Science),2002, 85 (3) : 43-51.
DOI: 10.1002/ecjc.1078 ( 0) 0)
|
| [3] |
YANNIPRINCY B, SRIDHAR S. Prediction of software reliability using cobb-douglas model in SRGM[J].
Journal of Theoretical and Applied Information Technology,2014, 62 (2) : 355-363.
( 0) 0)
|
| [4] |
YAMADA S, ICHIMONRI T, NISHIWAKI M. Optimal allocation policies for testing-resource based on a software reliability growth model[J].
Mathematical and Computer Modelling,1995, 22 (10) : 295-301.
DOI: 10.1016/0895-7177(95)00207-I ( 0) 0)
|
| [5] |
OKAMURA H, DOHI T. A novel framework of software reliability evaluation with software reliability growth models and software metrics[C]// Proceedings of the IEEE 15th International Symposium on High-Assurance Systems Engineering (HASE), Miami Beach: IEEE, 2014: 97-104. [DOI: 10.1109/HASE.2014.22.]
( 0) 0)
|
| [6] |
HUANG C Y, LYU M R. Optimal release time for software systems considering cost, testing-effort, and test efficiency[J].
IEEE Transactions on Reliability,2005, 54 (4) : 583-591.
DOI: 10.1109/TR.2005.859230 ( 0) 0)
|
| [7] |
PHAM H, ZHANG Xuemei. An NHPP software reliability model and its comparison[J].
International Journal of Reliability, Quality and Safety Engineering,1997, 4 (3) : 269-282.
DOI: 10.1142/S0218539397000199 ( 0) 0)
|
| [8] |
PHAM H, NORDMANN L, ZHANG Xuemei. A general imperfect-software-debugging model with S-shaped fault-detection rate[J].
IEEE Trans on Reliability,1999, 48 (2) : 169-175.
DOI: 10.1109/24.784276 ( 0) 0)
|
| [9] |
GOEL A L, OKUMOTO K. Time-dependent error-detection rate model for software reliability and other performance measures[J].
IEEE Transactions on Reliability,1979, R-28 (3) : 206-211.
DOI: 10.1109/TR.1979.5220566 ( 0) 0)
|
| [10] |
JHA P C, GUPTA D, YANG Bo, et al. Optimal testing resource allocation during module testing considering cost, testing effort and reliability[J].
Computers & Industrial Engineering,2009, 57 (3) : 1122-1130.
DOI: 10.1109/PRDC.2004.1276561 ( 0) 0)
|
| [11] |
YAMADA S, HISHITANI J, OSAKI S. Software-reliability growth with a Weibull test-effort: a model and application[J].
Reliability, IEEE Transactions on Reliability,1993, 42 (1) : 100-106.
DOI: 10.1109/24.210278 ( 0) 0)
|
| [12] |
HUANG C Y, LO J H. Optimal resource allocation for cost and reliability of modular software systems in the testing phase[J].
Journal of Systems and Software,2006, 79 (5) : 653-664.
DOI: 10.1016/j.jss.2005.06.039 ( 0) 0)
|
| [13] |
张策, 孟凡超, 崔刚, 等. SRGM中TE建模机制与模型比较分析[J].
哈尔滨工业大学学报,2015, 47 (5) : 32-39.
DOI: 10.11918/j.issn.0367-6234.2015.05.006 ZHANG Ce, MENG Fanchao, CUI Gang, et al. Overview of modeling of TE in SRGM and comparisons for models[J]. Journal of Harbin Institute of Technology,2015, 47 (5) : 32-39. DOI: 10.11918/j.issn.0367-6234.2015.05.006 (  0) 0)
|
| [14] |
HUANG C Y. Cost-reliability-optimal release policy for software reliability models incorporating improvements in testing efficiency[J].
Journal of Systems and Software,2005, 77 (2) : 139-155.
DOI: 10.1016/j.jss.2004.10.014 ( 0) 0)
|
| [15] |
AHMAD N, KHAN M G M, QUADRI S M K, et al. Modelling and analysis of software reliability with Burr type X testing-effort and release-time determination[J].
Journal of Modelling in Management,2009, 4 (1) : 28-54.
DOI: 10.1108/17465660910943748 ( 0) 0)
|
| [16] |
张策, 崔刚, 刘宏伟, 等. 软件测试资源与成本管控和最优发布策略[J].
哈尔滨工业大学学报,2014, 46 (5) : 51-58.
DOI: 10.11918/j.issn.0367-6234.2014.05.009 ZHANG Ce, CUI Gang, LIU Hongwei, et al. Software test resources and cost control and optimal release policy[J]. Journal of Harbin Institute of Technology,2014, 46 (5) : 51-58. DOI: 10.11918/j.issn.0367-6234.2014.05.009 (  0) 0)
|
| [17] |
LIN C T. Analyzing the effect of imperfect debugging on software fault detection and correction process via a simulation framework[J].
Mathematical and ComputerModelling,2011, 54 (11/12) : 3046-3064.
DOI: 10.1016/j.mcm.2011.07.033 ( 0) 0)
|
| [18] |
MANJULA T, JAIN M, GULATI T R. Cost optimization of a software reliability growth model with imperfect debugging and a fault reduction factor[J].
Anzam Journal,2014, 55 : 182-196.
( 0) 0)
|
| [19] |
JAIN M, MANJULA T, GULATI T R. Imperfect debugging study of SRGM with fault reduction factor and multiple change point[J].
International Journal of Mathematics in Operational Research,2014, 6 (2) : 155-175.
DOI: 10.1504/IJMOR.2014.059526 ( 0) 0)
|
| [20] |
PENG R, LI Y F, ZHANG W J, et al. Testing effort dependent software reliability model for imperfect debugging process considering both detection and correction[J].
Reliability Engineering & System Safety,2014, 126 : 37-43.
DOI: 10.1016/j.ress.2014.01.004 ( 0) 0)
|
| [21] |
YAMADA S, OHBA M, OSAKI S. S-shaped reliability growth modeling for software error detection[J].
Reliability, IEEE Transactions on Reliability,1983, R-32( (5) : 475-484.
DOI: 10.1109/TR.1983.5221735 ( 0) 0)
|
| [22] |
BOKHARI M U, AHMAD N. Incorporating burr type XII testing-efforts into software reliability growth modeling and actual data analysis with applications[J].
Journal of Software,2014, 9 (6) : 1389-1400.
DOI: 10.4304/jsw.9.6.1389-1400 ( 0) 0)
|
| [23] |
OHBA M. Software reliability analysis models[J].
IBM Journal of research and Development,1984, 28 (4) : 428-443.
DOI: 10.1147/rd.284.0428 ( 0) 0)
|
| [24] |
WOOD A. Predicting software reliability[J].
Computer,1996, 29 (11) : 69-77.
DOI: 10.1109/2.544240 ( 0) 0)
|
| [25] |
EHRLICH W, PRASANNA B, STAMPFEL J, et al. Determining the cost of a stop-test decision (software reliability)[J].
IEEE Software,1993, 10 (2) : 33-42.
DOI: 10.1109/52.199726 ( 0) 0)
|
| [26] |
GOPALAKRISHNA R, SPAFFORD E, VITEK J. Vulnerability likelihood: a probabilistic approach to software assurance. Technical Report 2005-06[R]. West Lafayette: Purdue University, 2005.
( 0) 0)
|
| [27] |
PHAM H. An imperfect-debugging fault-detection dependent-parameter software[J].
International Journal of Automation and Computing,2007, 4 (4) : 325-328.
DOI: 10.1007/s11633-007-0325-8 ( 0) 0)
|
| [28] |
AHMAD N, KHAN M G M, RAFI L S. A study of testing-effort dependent inflection S-shaped software reliability growth models with imperfect debugging[J].
International Journal of Quality & Reliability Management,2010, 27 (1) : 89-110.
DOI: 10.1108/02656711011009335 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


