自从第3次科技革命以来,能源成为各个国家的经济命脉.我国是一个能源生产大国和消费大国,拥有丰富的化石能源资源[1].在经济高速增长的条件下,我国能源的消耗速度比其他国家更快,能源枯竭的威胁可能来得更早、更严重[2].可再生能源的开发利用更加迫在眉睫,潮流能作为海洋可再生能源的一种,以其可持续、密度大、可预测的优势受到人们的青睐[3-4].
垂直轴潮流能水轮机由于旋转方向不受来流影响、叶片结构简单容易加工、工作速比低不易产生空化的优点备受关注.本文采用的垂直轴水轮机属于升力型,驱动水轮机转动的驱动力主要来自叶片的升力.在叶片旋转一周的过程中,叶片实际来流速度为远方水流速度与旋转速度两者的叠加,叶片的升阻力会随着叶片位置角变化而变化,升力沿轨迹圆切线的分量是驱动叶轮转动的主要动力来源.和涡方法、流管法相比,CFD方法能够获得更多的流场瞬时信息,且随着计算机的高速发展计算精度更加精确,所以CFD方法在垂直轴水轮机的应用非常广泛[5-8].迄今为止研究人员对单个垂直轴水轮机的研究已经取得了诸多成果,但随着能源需求加大,潮流能水轮机必将进入到双机组乃至多机组共同工作发电的时代.双机组垂直轴潮流能水轮机的研究还处于起步阶段,文献[9-10]利用涡方法和实验方法研究水轮机旋转方向、水轮机间距和来流攻角对水轮机效率的影响,得出这3个因素变化时会对输出功率和转矩振动方面存在有利和有害干扰.文献[11]对四叶片对转双机组垂直轴水轮机进行水动力性能研究,当2个直径为4 m、水轮机间距为0.5 m时效率最大.文献[12-13]分别对垂直轴水轮机机群进行了模拟,绘制了不同排布形式的水轮机群效率与叶尖速比的曲线,为多机组的水轮机排布提出了意见.
文献[9]提出初始相位角的不同对水轮机的水动力性能会产生影响,但它们并没有对其进行研究分析.本文针对该问题利用CFX软件进行垂直轴潮流能水轮机的初始相位角研究,通过改变水轮机的叶片数来改变密实度,对比不同相位角对两个机组的效率-速比曲线的影响,并对不同相位角的压力云图进行分析比较.
1 理论基础垂直轴水轮机来流速度为v,水轮机直径为D,半径为R, 叶片数为Z,旋转角速度为ω,垂直轴水轮机转动过程中某一时刻单个叶片的运动如图 1所示(以三叶片为例),θ为叶片位置角,本文中的水轮机属于固定偏角式水轮机[14].
为了方便分析,定义量纲一的参数如下:
| $ \begin{array}{l} \sigma {\rm{=}}ZD/\pi D, \\ {C_1}={F_1}/\left({0.5\rho {v^2}Cb} \right), \\ {C_n}={F_n}/\left({0.5\rho {v^2}Cb} \right), \\ {C_p}=M\omega /\left({0.5\rho {v^2}Db} \right), \\ \lambda=\omega R/v. \end{array} $ |
式中:Ft为叶片切向力,N;Fn为叶片法向力,N;C为弦长,m;b为展长,m;M为水轮机转矩,N·m;ω为水轮机旋转角速度,rad/s.
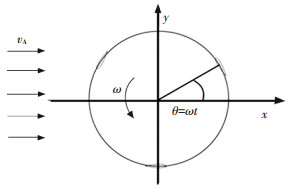
|
图 1 叶片的运动分析 Figure 1 The motion analysis of blade |
为了验证本文所选用的CFX软件在模拟垂直轴潮流能水轮机水动力性能的可靠性,选取经典单个垂直轴水轮机实验模型进行对比.1979年,美国德克萨斯科技大学的Strickland教授为了方便测量和记录,将垂直轴风机叶片在水池中进行实验.选取其中一种两叶片垂直轴模型进行对比,模型直径D为1.22 m,叶片翼型NACA0012,密实度为0.048,速比为7.5.对选取的水轮机模型进行网格划分,方法参照李志川[14]在垂直轴水轮机的数值模拟研究中给出入口边界条件为速度入口,出口为压力出口,计算场域边界为自由滑移边界,叶片表面选用无滑移边界条件,湍流模型选取SST模型,计算时间步长为旋转域旋转3°时所需的时间,计算15个周期使计算结果充分收敛.模型旋转域网格数为31 630,外域网格数为20 960,旋转域中叶片周围网格加密作为边界层,第1层网格高度为叶片弦长的0.001倍,有利于提高技术精度.
将CFD数值模拟结果与实验结果对比,如图 2所示.从图 2中可以看出,法向力系数曲线和切向力系数曲线在总体趋势上拟合程度较高.法向力系数平均值误差为4.9%,切向力系数平均值误差为2.1%,误差小于5%,因此验证了本文CFD方法的可行性.
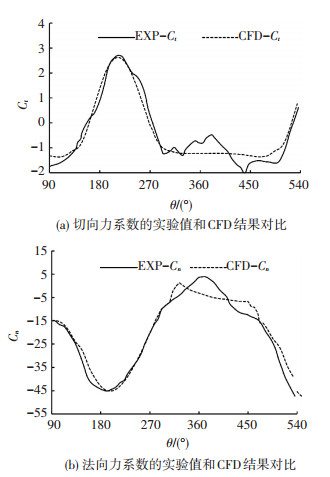
|
图 2 实验值和CFD结果对比曲线 Figure 2 Comparison between calculated and experimental values |
本文采用了哈尔滨工程大学自行设计的双机组垂直轴潮流能水轮机模型.单机直径D=4 m,翼型为NACA0018,弦长C=0.6 m,两机组间距为0.6 m,叶片数Z=2、3、4,密实度分别为0.095 5、0.143 0、0.191 0这3种密实度不同的双机组垂直轴水轮机,水轮机旋转域网格,如图 3所示.

|
图 3 不同密实度水轮机网格 Figure 3 Gird distribution of different density of turbines |
双机组水轮机在初始时刻的相位角定义以二叶片为例,如图 4所示.机组分为1号、2号机组,1号机组叶片2弦长与水流方向平行(即不同叶片数的一号机组始终有一个叶片在位置角270°),2号机组定义叶片3轴心到叶轮轴心的连线和Y轴方向夹角为相位角,用σ表示,如图 4所示相位角为30°.即在改变相位角时,只有2号机组的叶片位置在变化,1号机组叶片位置不变.两叶片水轮机的相位角σ为0°、30°、60°、90°、120°、150°,中间相位角为90°.三叶片水轮机的相位角σ为0°、30°、60°、90°,中间相位角为60°.四叶片水轮机的相位角σ为0°、15°、30°、45°、60°、75°,中间相位角为45°.另外计算单个机组水轮机在敞水域中的水动力模型作为对比,用single表示.
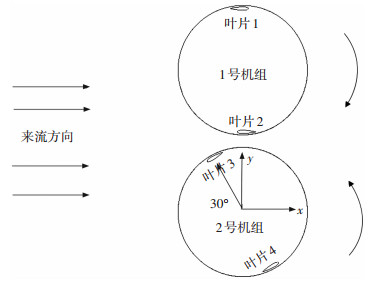
|
图 4 初始相位角定义 Figure 4 Definition of initial phase angle |
本文利用CFX软件模拟双机组垂直轴潮流能水轮机在敞水域中的运行状态,来流速度为vA=3 m/s, 叶尖速比分为0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5共9个工况.
如图 5所示,密实度不同的双机组水轮机的初始相位角在变化时,各个机组的效率曲线都会有相应变化.通过对比图 5(a)~(f)的效率变化曲线可以看出,双机组的各个水轮机效率明显比单个机组的效率要高,特别在中高速比时更加明显;不同密实度的水轮机效率曲线随相位角变化的规律相似:在不考虑相位角为0°时的情况下,1号机组随着初始相位角的变大,中高速比下的效率逐渐减小,2号机组随着初始相位角的变大,中高速比下的效率逐渐变大.相位角为0°时,两个机组的效率曲线和中间相位角效率曲线基本重合,即两叶片水轮机的0°相位角效率曲线和90°相位角效率曲线相近,三叶片水轮机的0°相位角效率曲线和60°相位角效率曲线相近,四叶片0°相位角效率曲线和45°相位角效率曲线相近.
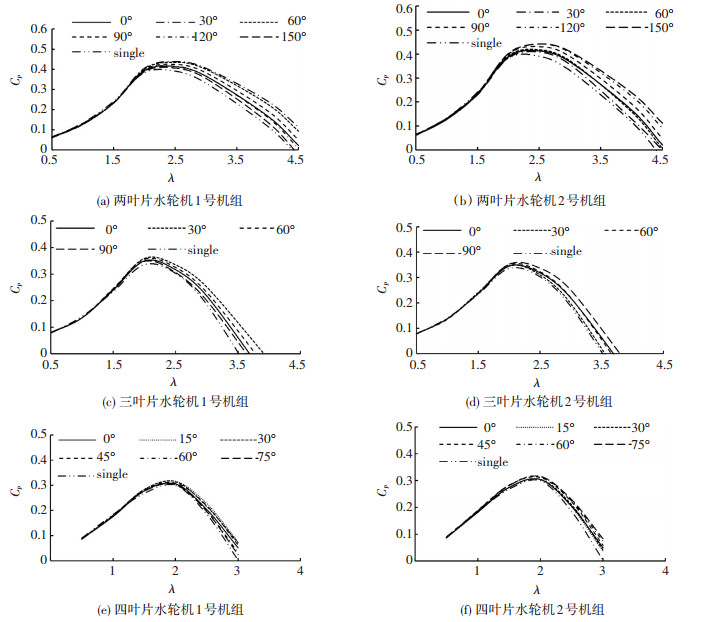
|
图 5 不同密实度水轮机组的效率随相位角变化规律曲线 Figure 5 The efficiency curves of different density turbines under different phase angles |
如图 6为两叶片双机组水轮机在不同相位角下的两个机组和单机组敞水域的效率曲线对比曲线,从图 6(a)~(d)中可以看出,相位角的变化对双机组水轮机两个机组的效率有很大影响.0°相位角时两个机组效率曲线相近,基本重合.30°时两个机组效率差最大,随着相位角的增大,两个机组的效率差逐渐减小,到90°相位角时两个机组效率曲线基本重合,随着相位角持续增大,两个机组间的效率差逐渐变大,到150°时达到最大.所以相位角从30°~150°,两叶片双机组水轮机的两个机组间的效率差先减小后增大,在相位角为90°时效率最接近.相位角为90°时,1号机组的叶片2和2号机组的叶片3间距最远,两叶片之间的干扰较小,使两个机组的效率相互影响较小,发电功率相近.在双机组水轮机实际工作中两个机组发电功率相近更有利于电能的输出控制[15],所以从这方面考虑选取0°和90°相位角较优.
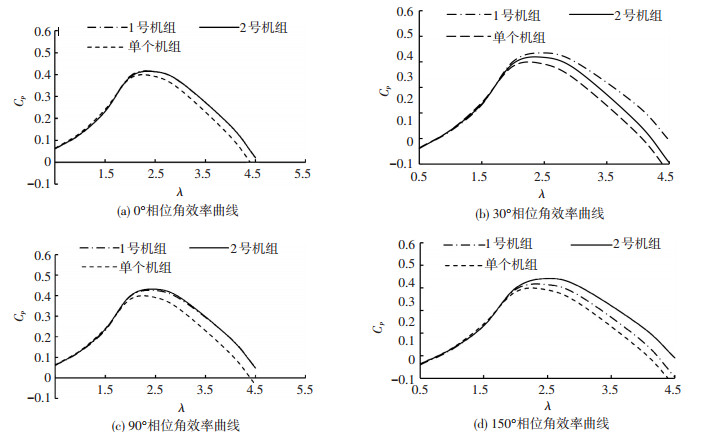
|
图 6 两叶片水轮机的两个机组的效率曲线对比图 Figure 6 The efficiency curves comparison between two units of two blades turbine |
如图 7(a)为三叶片双机组水轮机在60°相位角时的效率对比图,从图中可以看出此相位角下,两个机组效率曲线基本重合;图 7(b)为四叶片双机组水轮机在45°相位角时的效率对比图,此时两个机组的效率也基本相同.通过对比不同相位角下的效率变化情况,三叶片和四叶片双机组水轮机两个机组效率的变化规律和两叶片的相同.不同密实度的双机组水轮机效率随相位角变化规律相同.随着相位角增大,两个机组之间的效率差逐渐变小,当达到中间相位角时,效率差基本为0,相位角继续增大,效率差逐渐变大.所以不同密实度水轮机在对应的中间相位角时,两个机组效率相近,有利于电能的输出控制.
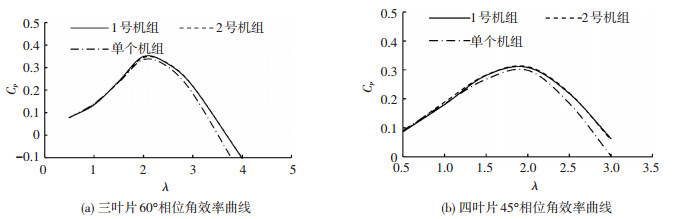
|
图 7 三、四叶片水轮机中间相位角效率曲线 Figure 7 The efficiency curves of three and four baldes turbines under middle phase angles |
如图 8为两叶片双机组水轮机在不同初始相位角情况下,选取2号机组的叶片在同一位置角时的压力云图进行对比分析.从图 8中可以明显看出在相位角为0°、30°、120°、150°的情况下,两个机组之间的叶尖高压区域相互连接,说明此相位角时的两机组叶片距离较近影响较大,60°时的两个机组高压区域未连接但高压区域远大于90°中间相位角.通过分析各相位角的压力云图,90°相位角时两个叶轮的高压区域没有相互连接且高压区域最小,则90°相位角时两个叶轮受到的压力最小,且两个叶轮间相互影响最小.
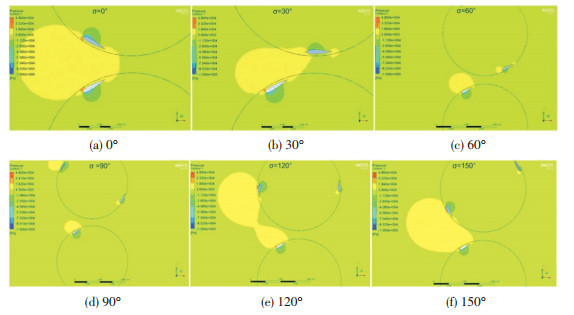
|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第8期) 图 8 两叶片双机组水轮机不同相位角压力云图 Figure 8 The pressure diagram of two blades twin-turbines under different phase angles |
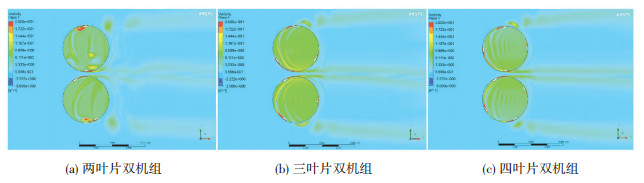
如图 9为三叶片双机组水轮机在中间相位角60°和四叶片水轮机在中间相位角45°时叶尖高压区域最小且两个机组高压区域未连接,和两叶片双机组水轮机的规律相符,在各自中间相位角时两个机组叶片之间相互影响最小且受到的压力最小.图 10为不同密实度双机组水轮机的涡量图.从图 10中可以看出,双机组水轮机旋转过程中每个叶片都有尾涡的脱落,脱落的尾涡随着水流向下游运动,在运动过程中会遇到其他叶片产生的尾涡,使这一区域水流复杂,两个水轮机之间的区域明显受到脱落的尾涡的相互影响,使经过这一区域的叶片前缘水流速度发生变化,导致水轮机效率发生变化,并且使叶片的压力增大,对水轮机组的安全性有一定影响.
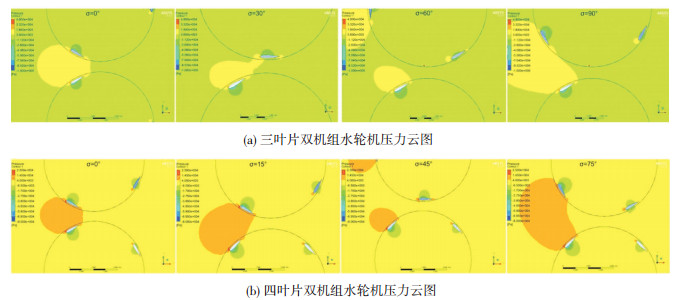
|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第8期) 图 9 三、四叶片双机组水轮机压力云图 Figure 9 The pressure diagram of three and four blades twin-turbines under different phase angles |
|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第8期) 图 10 不同密实度水轮机的涡量图 Figure 10 The vortical contour of twin-turbines under different densities |
在各个不同密实度的双机组水轮机处于各自的中间相位角时,叶片之间相互影响较小,受到的压力较小,选取中间相位角作为初始相位角能够提高水轮机组的安全性,增加水轮机运行的寿命.
4 结论1)不同密实度的双机组垂直轴水轮机的初始相位角对各个机组的效率影响较大,不考虑0°相位角情况下,随着相位角的变大,1号机组在中高速比的效率逐渐变小,2号机组的效率逐渐变大,这样可以通过调节相位角来控制两个机组的功率输出,以达到对功率输出的要求.
2)不同密实度的双机组水轮机在中间相位角时效率差基本为0,随着相位角增大或减小,效率差都会增大,两个机组间发电功率差距变大,不利于电能输出控制.
3)中间相位角时,机组叶尖高压区域最小,且两个机组的高压区域没有相连,两个机组叶轮间相互影响较小.选取中间相位角作为初始相位角能够减小叶尖压力,提高水轮机使用寿命.
| [1] |
张亮, 李志川, 张学伟, 等. 垂直轴潮流能水轮机研究与利用现状[J].
应用能源技术,2011 (9) : 1-7.
DOI: 10.3969/j.issn.1009-3230.2011.09.001 ZHANG Liang, LI Zhichuan, ZHANG Xuewei, et al. The status of research and application of vertical axis tidal turbine[J]. Applied Energy Technology,2011 (9) : 1-7. DOI: 10.3969/j.issn.1009-3230.2011.09.001 (  0) 0)
|
| [2] |
戴军, 单忠德, 王西峰, 等. 潮流水轮机的研究进展[J].
可再生能源,2010, 28 (4) : 130-133.
DOI: 10.3969/j.issn.1671-5292.2010.04.031 DAI Jun, SHAN Zhongde, WANG Xifeng, et al. Current research progress of water turbine[J]. Renewable Energy,2010, 28 (4) : 130-133. DOI: 10.3969/j.issn.1671-5292.2010.04.031 (  0) 0)
|
| [3] |
ROURKE O, BOYLE F, REYNOLDS A. Tidal energy update 2009[J].
Applied Energy,2010, 87 (2) : 398-409.
DOI: 10.1016/j.apenergy.2009.08.014 ( 0) 0)
|
| [4] |
BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. The prediction of the hydrodynamic performance of marine current turbines[J].
Renewable Energy,2008, 33 (5) : 1085-1096.
DOI: 10.1016/j.renene.2007.05.043 ( 0) 0)
|
| [5] |
李志川, 张亮, 孙科, 等. 垂直轴潮流水轮机数值模拟研究[J].
太阳能,2011, 32 (9) : 1321-1326.
LI Zhichuan, ZHANG Liang, SUN Ke, et al. Numerical Simulation of Vertical Axis Tidal Turbine[J]. Acta Energiae Solaris Sinica,2011, 32 (9) : 1321-1326. (  0) 0)
|
| [6] |
盛其虎, 周念福, 张学伟, 等. 二维垂直轴水轮机强迫振荡水动力性能分析[J].
哈尔滨工程大学学报,2015, 36 (1) : 41-45.
DOI: 10.3969/j.issn.1006-7043.201312038 SHENG Qihu, ZHOU Nianfu, ZHANG Xuewei, et al. Hydrodynamic performance analysis of a 2D vertical current turbine with forced oscillation[J]. Journal of Harbin Engineering University,2015, 36 (1) : 41-45. DOI: 10.3969/j.issn.1006-7043.201312038 (  0) 0)
|
| [7] |
STRICKLAND J H, WEBSTER B T, NGUYEN T. A vortex model of the Darrieus turbine: an analytical and experimental study[J].
Journal of Fluids Engineering,1979, 80 (4) : 500-505.
DOI: 10.1115/1.3449018 ( 0) 0)
|
| [8] |
季剑远.可控偏角竖轴水轮机性能试验研究[D].哈尔滨:哈尔滨工程大学, 2008.
JI Jianyuan. Experimental study on the performance of controlled vertical-axis variable-pitch turbine[D]. Harbin: Harbin Engineering University, 2008. (  0) 0)
|
| [9] |
LI Ye, CALISAL S M. Modeling of twin-turbine systems with vertical axis tidal current turbines: Part I-Power output[J].
Ocean Engineering,2010, 37 (7) : 627-637.
DOI: 10.1016/j.oceaneng.2010.01.006 ( 0) 0)
|
| [10] |
LI Ye, CALISAL S M. Modeling of twin-turbine systems with vertical axis tidal current turbines: Part II-torque fluctuation[J].
Ocean Engineering,2011, 38 (4) : 550-558.
DOI: 10.1016/j.oceaneng.2010.11.025 ( 0) 0)
|
| [11] |
KHALID S S, ZHANG Liang, SHENG Qihu. CFD simulation of twin vertical axis tidal turbines system[J].
Research Journal of Applied Sciences, Engineering and Technology,2013, 5 (1) : 233-238.
( 0) 0)
|
| [12] |
郭峰山.竖轴潮流能水轮机性能分析及机群排布优化[D].大连:大连理工大学, 2013.
GUO Fengshan. Performance analysis of vertical-axis tidal current turbines and optimizing turbines array[D]. Dalian: Dalian University of Technology, 2013. (  0) 0)
|
| [13] |
GOUDE A, AGREN O. Numerical simulation of a farm of vertical axis marine current turbines[C]//Proceedings of the 29th International Conference on Offshore Mechanics and Arctic Engineering. Shanghai: ASME, 2010: 335-344.[DOI:10.1115/OMAE2010-20160.]
( 0) 0)
|
| [14] |
李志川.垂直轴潮流能水轮机水动力特性数值模拟与试验研究[D].哈尔滨:哈尔滨工程大学, 2011.
LI Zhichuan. Numerical simulation and experimental study on hydrodynamic characteristic of vertical axis tidal turbine[D].Harbin: Harbin Engineering University, 2011. (  0) 0)
|
| [15] |
BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. The prediction of the hydrodynamic performance of marine current turbines[J].
Renewable Energy,2008, 33 (5) : 1085-1096.
DOI: 10.1016/j.renene.2007.05.043 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


