2. 中交公路规划设计院有限公司, 北京 100088 ;
3. 广东省交通规划设计研究院股份有限公司, 广州 510507
2. CCCC Highway Consultants Co. Ltd., Beijing 100088, China ;
3. Guangdong Province Communications Planning & Design Institute Co., Ltd., Guangzhou 510507, China
随着经济全球化进程的不断推进以及我国“一带一路”战略构想的倡导,我国交通基础设施建设行业将有更多机会参与到国际工程建设中. 在海外工程建设中,设计与施工采用的规范和标准是桥梁工程建设安全性与经济性的重要影响因素. 目前,能代表国际先进水平的国外公路桥梁规范和标准主要有两部:美国公路桥梁设计规范(AASHTO LRFD)和欧洲桥梁设计规范Eurocode(EN)[1-2]. 在海外工程设计与建设中,桥梁设计规范的选择除由政府部门的相关规定外,还需要基于不同桥规的对比与评价结果. 本文以公路桥梁为对象,建立针对中美欧桥梁设计规范的综合评价体系,提出评价基本指标与核心指标,系统地对中美欧公路混凝土桥梁设计规范的安全性和经济性进行评价与分析.
1 概率极限状态设计方法 1.1 目标可靠指标公路桥梁设计规范(下文简称为“桥规”),中外大多采用了以可靠度理论为基础的概率极限状态设计方法,并提出了桥梁结构的目标可靠设计指标. 运用概率极限状态设计方法进行公路桥梁结构设计时,首先是要选用多大的结构失效概率进行结构设计,即确定结构的目标可靠指标. 目标可靠指标直接影响到桥梁工程的安全性和经济性[3-4]. 中美欧桥规中均对桥梁结构的目标可靠指标作出了规定与说明. 经理论换算,中美欧桥规基于100 a设计基准期的结构目标可靠指标及相应的结构失效概率见表 1.
| 表 1 设计基准期为100 a的目标可靠指标 Table 1 The target reliability index of the 100-year design reference period |
从表 1可以看出,中美欧桥规均将桥梁结构划分为3个等级,且中国桥规还区分了延性破坏与脆性破坏的目标可靠指标. 为便于对比,本文采用中国桥规中的延性破坏可靠指标与欧美桥规进行比较. 对比分析中假定中美欧桥规材料指标、几何特性、作用效应的概率模型基本相近. 桥梁结构设计基准期为100 a的目标可靠指标明显有中国桥规大于欧洲桥规大于美国桥规的结果;失效概率则有美国桥规大于欧洲桥规大于中国桥规的结果. 仅从桥梁结构的目标可靠指标来看,采用中国桥规进行桥梁工程设计是最安全的,欧洲桥规次之,美国桥规的安全余地相对最小.
1.2 分项系数概率极限状态设计在概率极限状态设计方法中,工程结构在设计使用期内结构各项功能与指标是否满足预定要求,通常采用“极限状态”来衡量与界定. 中欧桥规将极限状态划分为承载能力极限状态与正常使用极限状态;而美国桥规更细致地划分为5个极限状态:强度极限状态、使用极限状态、疲劳与断裂极限状态以及极端事件极限状态[5-6],其中前两者与中欧规范相对应. 本文建立的评价体系主要考虑最基本的承载能力与正常使用两种极限状态.
结构极限状态设计的基本变量通过概率分析取其代表值,以基本变量的分项系数来反映其变异性,并通过可靠度计算分析以及工程经验优先确定. 该设计方法亦称为半概率极限状态设计法,其分项系数明确体现了可靠度设计的基本理念. 本文根据结构目标可靠指标以及不同极限状态、不同构件、不同可靠指标水平建立中美欧桥规的评价指标.
1.3 极限状态可靠指标 1.3.1 承载能力极限状态可靠指标在承载能力极限状态下不同构件类型、结构跨径、截面形式均会影响结构构件可靠度的水平,需要大量的试验数据与工程经验积累. 文献[7]中给出了经过大量试验数据处理与概率模型计算的5种典型构件的平均可靠指标,如表 2所示.
| 表 2 5种典型构件的平均可靠指标 Table 2 Average reliability index of five typical components |
可以看出,活载效应服从正态分布时,构件可靠指标偏高. 因此对5种典型构件的平均可靠度均取活载效应服从极值I型时的计算结果.
1.3.2 正常使用极限状态可靠指标目前中美欧桥规均未给出正常使用极限状态设计的目标可靠指标规定. 国际结构安全度联合委员会(JCSS)根据结构安全等级,提出了正常使用极限状态下结构的目标可靠指标参考建议值βT分别为 2.3(一级)、1.7(二级)和1.3(三级)[8]. 针对结构构件正常使用阶段,本文主要选取结构变形(挠度)、抗裂性(裂缝)、构件应力3个方面进行可靠度分析. 其中,抗裂性主要考虑混凝土截面主拉应力可靠指标,构件应力考虑混凝土法向压应力可靠指标,该指标也作为承载能力极限状态验算的补充,其可靠指标水平相对偏高(参照表 1). 根据已有的理论与试验研究成果[9-10],正常使用极限状态下结构挠度、混凝土主拉应力、混凝土法向压应力指标的常用可靠指标范围分别为1.6~3.5、1.7~4.0、3.3~5.2. 以上极限状态控制可靠指标均将作为中美欧桥规评价体系的评价参考指标.
2 评价核心指标 2.1 评价基本指标 2.1.1 截面富余度在中、欧桥规承载能力极限状态与美国桥规强度极限状态下,将结构构件各设计控制截面的抗力效应设计值与作用效应组合设计值之比作为承载能力极限状态的主要研究指标,定量化反映承载能力极限状态下结构构件的承载能力,并定义该指标为截面富余度,即
| ${{\lambda }_{S}}=\frac{{{R}_{d}}}{{{S}_{d}}}\ge 1.0.$ | (1) |
式中Rd为截面的抗力效应设计值,Sd为截面的作用组合效应设计值.
λS是承载能力极限状态下截面抗力效应和截面作用效应的综合体现,能够反映截面的安全程度,也可反映截面材料的利用率. 针对桥梁结构构件主要受力形式(主要分为受弯、受剪、轴心受压、偏心受压等),将承载能力极限状态下的截面富余度λS根据公路混凝土桥梁结构构件主要内力效应的不同,简要划分为截面抗弯富余度λsb、截面抗剪富余度λSS与截面抗压富余度λsa3个二级指标.
2.1.2 变形富余度在中、欧桥规正常使用极限状态下与美国桥规使用极限状态下,均对结构的适用性与耐久性提出了要求[11-12]. 为从正常使用极限状态下结构的使用性能指标上来比较桥梁规范的经济性与安全性,采用桥规规定的结构限值与结构构件的实际变形值的比值作为正常使用极限状态的主要评价指标之一,定义该指标为变形富余度,即
| ${{\lambda }_{W}}=\frac{{{w}_{A}}}{{{w}_{R}}}\ge 1.0.$ | (2) |
式中wA为桥梁设计规范规定的变形限值,wR为桥梁结构的计算变形.
λW是中美欧桥规正常使用极限状态下结构构件适用性与经济性的体现,能够间接反映构件的安全程度. 中美欧桥梁设计规范均对桥梁构件的最大挠度给出了限值,并规定了结构变形的计算方法.
2.1.3 应力富余度在正常使用极限状态下,中美欧桥规均要求进行构件抗裂性、裂缝宽度及变形验算. 其中混凝土构件的抗裂性验算以结构构件正截面与斜截面混凝土拉应力是否超过限值作为判断标准. 同时中美欧桥规在承载能力极限状态,除了计算构件的极限承载力,还需要进行弹性阶段构件应力验算,包括混凝土的法向压应力、斜截面混凝土的主压应力、钢筋拉应力等,并作为构件承载力计算的补充. 因此结构构件的应力计算涉及到承载能力及正常使用两类极限状态. 采用桥梁设计规范规定的构件截面应力限值与计算应力的比值作为承载能力及正常使用极限状态的补充评价指标,定义该指标为应力富余度,即
| ${{\lambda }_{\sigma }}=\frac{{{\sigma }_{l}}}{{{\sigma }_{r}}}\ge 1.0.~$ | (3) |
式中σl为桥规规定的不同设计状况下构件截面的应力限值,σr为相应作用效应组合作用下构件截面的计算应力值.
根据不同设计状况下的不同应力验算要求,将λσ划分为两个二级应力富余度指标:1)构件承载力补充验算时构件截面法向压应力富余度λσc;2)正常使用极限状态下,抗裂性验算时构件截面混凝土(主)拉应力富余λσt.
2.2 评价核心指标λS、λW、λσ3个评价基本指标,以及λsb、λss、λsa、λσc、λσt5个评价二级指标分别从承载能力极限状态下不同构件抗力效应与作用效应综合对比角度,以及正常使用极限状态下结构构件功能限值与计算效应(变形、应力)综合对比角度,较全面给出了中美欧桥规的量化评价标准. 上述富余度评价指标在具体计算时,应根据不同规范、不同构件的计算方法与取值要求进行计算分析.
基于前文关于两种极限状态结构构件可靠指标研究成果,融合评价基本指标与二级指标的基本内容,针对不同富余度采用基于目标可靠指标的不同富余度分项权重,建立中美欧桥梁设计规范的评价核心指标,定义该指标为控制截面综合富余度,即
| $\begin{align} & {{\lambda }_{K}}={{\gamma }_{1}}\cdot (\sum {{\gamma }_{Si}}\cdot {{\lambda }_{Si}})+{{\gamma }_{2}}\cdot ({{\gamma }_{\sigma c}}\cdot {{\lambda }_{\sigma c}}+{{\gamma }_{W}}\cdot \\ & {{\lambda }_{W}}+{{\gamma }_{\sigma t}}\cdot {{\lambda }_{\sigma t}}). \\ \end{align}$ | (4) |
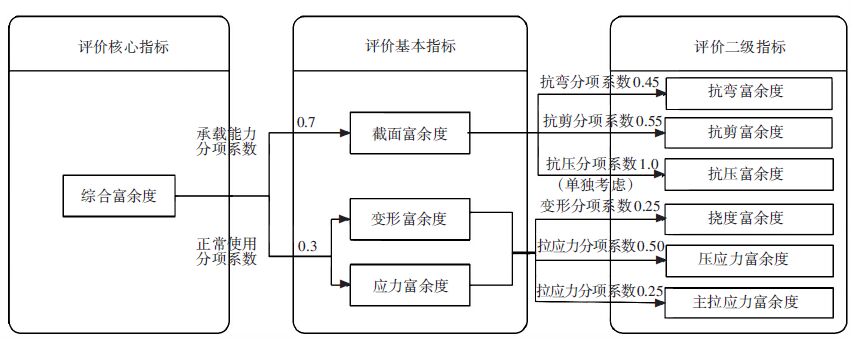
式中λK分为两部分:第1部分为承载能力极限状态的截面富余度组合,第2部分为正常使用极限状态的变形富余度、应力富余度组合. 其中,γ1、γ2分别为考虑中美欧桥规目标可靠指标下的承载能力极限状态、正常使用极限状态的基本分项权重,参考表 1与文献[8]可知,承载能力目标可靠指标平均值为3.975,正常使用目标可靠指标平均值为1.766. 根据不同极限状态下目标可靠指标平均值的比值,γ1、γ2分别取为0.7、0.3(见图 1).
|
图 1 综合富余度λK的计算模型 Figure 1 Calculation model of comprehensive surplus λK |
承载能力极限状态下,γSi为λsb、λss和λsa的二级分项权重,可具体表示为γsb、γss、γsa. 参考表 2,受弯构件平均可靠度为4.37,受剪构件平均可靠度为4.57,根据比值结果适当放大抗剪富余度权重,因此建议截面抗弯富余度分项权重γsb取0.45,截面抗剪富余度分项权重γss取0.55. 对于桥塔、桥墩等受压构件,认为其独立于受弯构件,目前的计算只考虑偏压效应,截面抗压富余度分项权重γsa取1.0.
正常使用极限状态下,γW为λW的分项权重,γσc、γσt分别为λσc和λσt的二级分项权重. 由前述内容可知,正常使用极限状态下结构挠度、混凝土主拉应力、混凝土法向压应力指标的可靠度均值分别为2.55、2.85、4.25,根据比值结果建议变形富余度分项权重γW取0.25,构件截面法向压应力富余度分项权重γσc取0.5,构件截面混凝土(主)拉应力富余度分项权重γσt取0.25.
根据以上内容采用层次分析法建立中美欧桥规评价层次模型,共3层评价指标结构:评价核心层为核心指标“综合富余度λK”,评价基本层为基本富余度计算指标:λS、λW、λσ,并考虑承载能力与正常使用极限状态的基本分项权重γ1、γ2;评价次级层为二级富余度指标λsb、λss、λsa、λσc、λσt,并考虑二级分项权重γsb、γss、γsa、γW、γσc、γσt等参数.
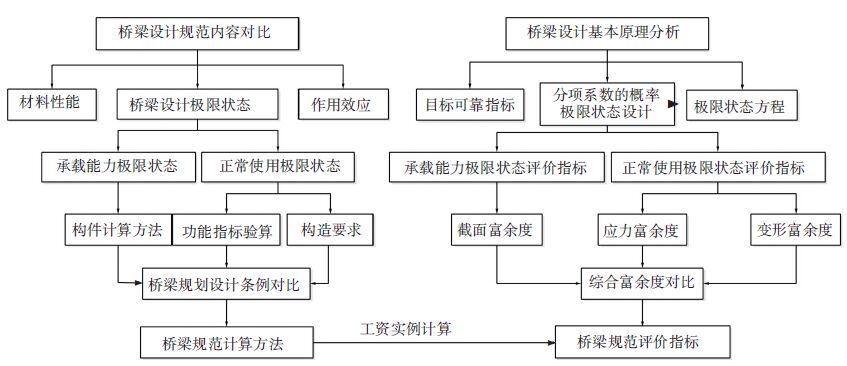
3 综合评价体系 3.1 评价体系内容中美欧公路混凝土桥梁设计规范的综合评价体系主要从两方面进行:1)桥梁设计规范内容对比,对比分析中美欧桥梁设计规范在设计准则、极限状态、材料特性、荷载组合、构件计算方法、构造要求等方面的差异,从理论内容层面进行中美欧桥梁设计规范计算方法与要求的对比分析. 2)规范评价指标分析,基于可靠度理论,得出中美欧桥规评价基本指标λS、λW、λσ与评价核心指标λK的计算方法,并以实际桥梁工程为评价算例,进行工程实例评价指标对比分析,系统全面的定量化计算、分析和描述中美欧桥梁设计规范的安全性与经济性. 中美欧公路混凝土桥梁设计规范综合评价体系的技术路线见图 2.
|
图 2 中美欧公路桥规评价体系 Figure 2 The evaluation system of Chinese,American and European specifications |
中美欧桥梁规范设计内容对比是中外桥规综合评价体系的基础,中美欧桥梁规范评价指标模式是中外桥规评价体系的核心内容.
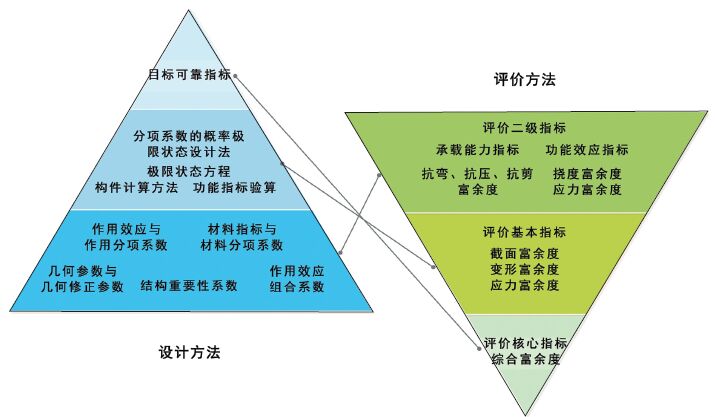
3.2 评价体系特性 3.2.1 评价方法与设计方法中美欧桥规的设计方法为“由整到零”,即从目标可靠指标βT出发,发散到不同极限状态设计,作用效应、抗力效应分项系数,结构构件功能限值等设计详细规定,设计过程由可靠度理论与概率模型计算贯穿始终. 而中美欧桥规的评价方法思路为“由零到整”,根据各桥规的具体要求,得到不同极限状态、不同构件、不同指标的评价基本指标(截面富余度λS、变形富余度λW、应力富余度λσ),并基于已有可靠指标的研究,最终回溯各项基本指标得到考虑富余度分项系数的核心评价指标:综合富余度λK. 中美欧桥规的评价方法也以可靠度原理为核心,以桥规各项规定为基础进行综合评价.目标可靠指标βT与综合富余度λK作为中美欧桥规的设计出发点与评价回归点,以可靠度理论为线索,将中美欧桥规的评价方法与设计方法对应连接. 中美欧桥规的设计方法与评价方法的路线图参见图 3.
|
图 3 中美欧桥规设计方法与评价方法的技术路线 Figure 3 Technical route of design and evaluation methods of Chinese,American and European specifications |
目标可靠指标βT与综合富余度λK是中美欧桥规设计方法与评价方法的核心指标. 通过上述综合富余度λK以及富余度基本指标、二级指标的计算方法介绍可以发现,可靠指标β、富余度λ与结构的可靠性具有相似的数学关系:公路桥梁结构构件可靠指标β越大,富余度λ越大,结构失效概率pf越小,结构构件安全储备越高. 反之亦然. 富余度λ作为中美欧桥规的评价指标与目标可靠指标βT具有良好的一致性. 在实际公路混凝土桥梁工程设计中可通过评价富余度指标λ来衡量不同桥梁设计规范的安全性与经济性.
4 工程评价实例参考上文的评价体系与评价指标的计算方法,以我国交通运输部在2008年颁布的公路桥梁通用图中不同配置的22座预应力混凝土简支T梁桥、预应力混凝土简支空心板梁桥、预应力混凝土箱型连续梁桥以及赤道几内亚Mbini混凝土斜拉桥为工程算例,分别根据中美欧桥规的荷载、材料和计算方法,按材料等强度换算原则进行工程算例的有限元计算分析. 工程算例的主要技术指标如表 3所示. 所有工程算例都采用公路I级汽车荷载,除预应力混凝土箱形连续梁桥混凝土采用C50外,其余混凝土都采用C45. 本文工程算例以预应力混凝土(以下简称PC)结构桥梁为主,对于钢筋混凝土桥梁可近似以裂缝宽度指标取代(主)拉应力指标.
| 表 3 工程算例主要技术指标 Table 3 Main technical indices of engineering examples |
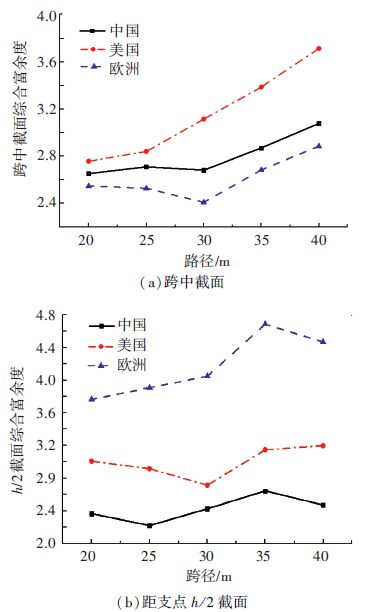
PC简支T梁桥与PC简支空心板梁桥均选取主梁最不利截面“跨中截面”与“距支点h/2处截面”进行综合富余度λK对比分析. 因相同跨径、不同桥宽的梁桥控制截面λK计算结果差异较小,这里主要着重列出相同桥宽、不同跨径的梁桥控制截面λK计算结果(见图 4、5).
|
图 4 PC简支T梁桥控制截面综合富余度λK Figure 4 The comprehensive surplus λK of control section of PC simply supported T-beam bridge |
|
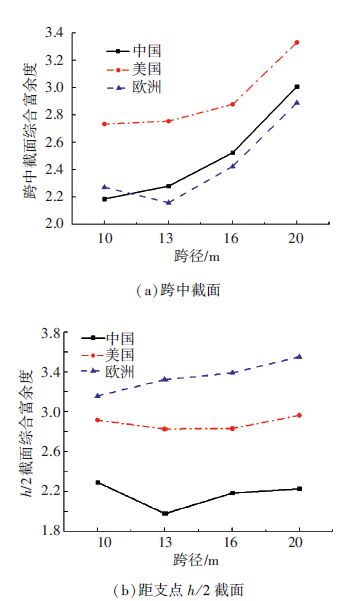
图 5 PC简支空心板控制截面综合富余度λK Figure 5 The comprehensive surplus λK of control section of PC simply supported hollow slab |
由图 4、5可知,对于弯矩效应控制的跨中截面,随着主梁跨径的变化,综合富余度λK:美国桥规的计算结果大于中国桥规大于欧洲桥规的计算结果,且中美欧桥规λK随着跨径增大,呈现逐步增大的变化趋势. 对于剪力效应控制的距支点h/2截面,随着主梁跨径变化,欧洲桥规的λK计算结果大于美国桥规大于中国桥规的计算结果.结果表明:采用相同材料强度关系转化后分析得到的PC简支T梁与PC简支空心板梁桥,欧美桥规的λK更大,安全储备更高;即当安全储备要求相同时,欧美桥规计算所需材料更少,经济性更好.
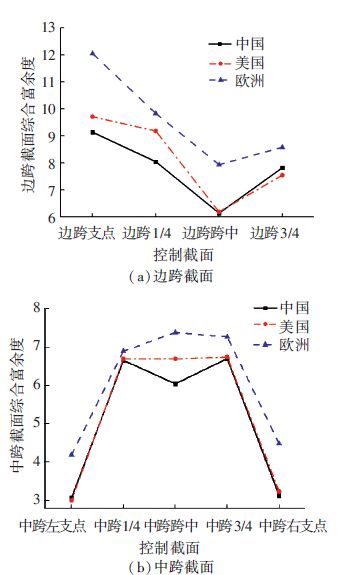
4×30 m预应力混凝土箱形连续梁桥选取9个控制截面,边跨与中跨控制截面λK计算结果如图 6所示. 连续箱梁桥各控制截面综合富余度λK的均值:中国桥规6.303,美国桥规6.555,欧洲桥规7.496,各控制截面λK有欧洲桥规大于美国桥规大于中国桥规. Mbini斜拉桥在中美欧桥规下主梁与塔柱控制截面的综合富余度λK计算结果见表 4. 该斜拉桥主梁各控制截面λK的均值:中国桥规2.770,美国桥规2.587,欧洲桥规3.258;各控制截面λK有欧洲桥规大于美国桥规和中国桥规. 该斜拉桥塔柱各控制截面λK的均值:中国桥规2.574,美国桥规3.128,欧洲桥规2.787;各控制截面λK有美国桥规大于欧洲桥规大于中国桥规.
|
图 6 连续箱梁桥控制截面综合富余度λK Figure 6 The comprehensive surplus λK of control section of continuous box girder bridge |
| 表 4 Mbini斜拉桥控制截面综合富余度 Table 4 The comprehensive surplus of control section of Mbini cable-stayed Bridge |
在中美欧桥规相同材料强度转化条件下进行的工程实例计算,即根据中国桥规的实际桥梁用材转化为对应欧美材料标准进行分析. 结果表明,中美欧桥规下工程实例的综合富余度λK具有相似规律:弯矩效应控制截面λK:美国桥规的计算结果大于中国桥规大于欧洲桥规的计算结果;剪力效应控制截面λK:欧洲桥规的计算结果大于美国桥规大于中国桥规的计算结果. 综合分析,欧美桥规的综合富余度λK更高,安全储备更高;即当安全储备要求相同时,欧美桥规计算所需材料更少,经济性更好.
5 结 论1) 中美欧桥规从设计基准期为100 a的目标可靠指标βT对比分析,有中国桥规大于欧洲桥规大于美国桥规的结果,即从桥梁设计目标可靠指标分析,依据中国桥规进行设计更为安全,欧洲次之,依据美国桥规设计则安全余地相对最小.
2) 建立了中外桥梁设计规范的综合评价体系. 该体系可分为两个层次:桥梁设计规范内容对比,对比分析中外桥规在设计准则、材料特性、荷载组合、构件计算方法等方面的差异;规范评价指标分析,采用基本指标“截面富余度λS”、“变形富余度λW”和“应力富余度λσ”,以及评价核心指标“综合富余度λK”可进行工程设计实例的安全性和经济性评价分析.
3) 根据不同配置的23座桥梁工程实例计算得到的综合富余度λK的计算结果可有欧美桥规大于中国桥规的结论,即相同材料强度条件下欧美桥规计算的工程实例的安全性更高,而中国桥规计算结果则经济性更好. 实际桥梁工程设计中,控制截面综合富余度λK可作为规范选择或桥梁安全性、经济性评价的依据之一.
| [1] |
American Association of State Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. 5th ed. Washington DC: American Association of State Highway and Transportation Officials, 2010.
( 0) 0)
|
| [2] |
British Standards Institution. Eurocode 2: design of concrete structures: BS EN 1992-2: 2005 [S]. London: British Standards Institution, 2005.
( 0) 0)
|
| [3] |
MULLAPUDI T R S, AYOUB A. Analysis of reinforced concrete columns subjected to combined axial, flexure, shear, and torsional loads[J].
Journal of Structural Engineering,2013, 139 (4) : 561-573.
DOI: 10.1061/(ASCE)ST.1943-541X.0000680 ( 0) 0)
|
| [4] |
柳颖臣.基于概率理论的预应力混凝土桥梁结构可靠度研究[D].长安:长安大学,2008.
LIU Yingchen. The research based on the probability theory for the pre-stressed concrete bridge structure reliability [D].Chang’an: Chang’an University,2008. (  0) 0)
|
| [5] |
MESKI F E, MABSOUT M, TARHINI K. Investigation of AASHTO live-load reduction in reinforced concrete slab bridges[J].
Journal of Bridge Engineering,2011, 16 (6) : 792-803.
DOI: 10.1061/(ASCE)BE.1943-5592.0000237 ( 0) 0)
|
| [6] |
TOBIAS D H. Perspectives on AASHTO load and resistance factor design[J].
Journal of Bridge Engineering,2011, 16 (6) : 684-692.
DOI: 10.1061/(ASCE)BE.1943-5592.0000286 ( 0) 0)
|
| [7] |
李扬海, 鲍卫刚, 郭修武, 等.
公路桥梁结构可靠度与概率极限状态设计[M]. 北京: 人民交通出版社, 1997 : 230 -245.
LI Yanghai, BAO Weigang, GUO Xiuwu, et al. Reliability and probability limit states design of highway bridge structure[M]. Beijing: China Communications Press, 1997 : 230 -245. (  0) 0)
|
| [8] |
Joint Committee on Structural Safety. The JCSS probabilistic model code [EB/OL]. [2015-05-06]. http://www.jcss.byg.dtu.dk/.
( 0) 0)
|
| [9] |
袁新朋.公路预应力混凝土桥梁的可靠度分析[D].成都:西南交通大学,2009.
YUAN Xinpeng. Reliability evaluation of highway prestressed concrete bridge [D].Chengdu: Southwest Jiaotong University,2009. (  0) 0)
|
| [10] |
张东东.混凝土梁式桥结构构件正常使用极限状态可靠性评估[D].长安:长安大学,2009.
ZHANG Dongdong. Evaluation on reliability of serviceability limit states for structural members of concrete beam bridge [D].Chang’an: Chang’an University, 2009. (  0) 0)
|
| [11] |
NOWAK A S, COLLINS K R.
Reliability of structures[M]. Boca Raton: CRC Press, 2012 : 107 -297.
( 0) 0)
|
| [12] |
BARKER R M, PUCKETT J A.
Design of highway bridges: An LRFD approach[M]. Hoboken: John Wiley&Sons, Inc, 2013 : 215 -322.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


