2. 黑龙江工程学院 汽车与交通工程学院,哈尔滨 150050 ;
3. 福州大学 土木学院,福州 350116
2. School of Automotive and Transportation Engineering, Heilongjiang Institute of Technology, Harbin 150050, China ;
3. College of Civil Engineering, Fuzhou University, Fuzhou 350116, China
为了保证城市综合客运交通系统结构的稳定发展,国家和各级地方政府均相继出台了多项鼓励公共交通发展的法律与规范,但在实际实施过程中,由于存在监管力量薄弱、公交服务部门违规运营、违规成本较低等诸多问题,在实践中往往很难达到预期的目标. 这就使得城市常规公共交通运营的有效监管成为一个突出的问题. 国内外学者对于公交管理与仿真方面开展了积极尝试,如DEFLORIO F P[1]通过仿真模拟公交系统随机最短路径对于出行者出行路径的影响,以期为资源合理利用提供支持;Li X等[2]以出行时间最小化为目标,确定了公交系统构建的边界客流密度,对于公交服务水平的改善具有积极意义. 陈宽民等[3]分析了城市快速轨道交通与常规公共交通之间的定价博弈,给出了二者定价的动态调整过程;王炜等[4]从网络服务供给与需求的协调关系出发,给出了公共交通系统服务水平的模糊聚类分析方法;刘惠玲等[5]建立了城市公交系统模型,给出了北京市公交系统的政策建议;唐旭南等[6]分析了城市公交系统的能源消耗结构,给出了结构调整合理化建议. 韩烈等[7]分析了早高峰单起点多讫点公共交通系统乘客乘车行为,建立了等价的数学优化模型描述均衡状态. 当前的研究主要集中在路经选择、公交服务水平改善、服务信息交换、公交监控系统、公交定价等方面,在公交监管博弈分析与仿真方面有待深入开展研究.
1 公交监管问题博弈分析与建模目前,我国现行的常规公共交通管理体制以企业自主运营方式为主,同时常规公交企业接受来自管理部门的监督与管理. 假设常规公交企业均具有逐利的本能,其进行生产活动或服务行为的最终目的是实现利益的最大化,但受制于管理部门的监管,公交企业的行为策略选择需考虑实际管理约束. 为此,公交企业在实际运营管理过程中存在两种策略:一是严格按照相关规定组织公交运营活动;二是违规操作,通过降低发车班次等方法获取额外收益.
管理部门的职能是在保证公交运营有序进行的同时,尽量减少监管成本,假定管理部门在监管过程中能够严格执法,发现公交企业的违法行为能够严格按照规定处理,不存在权力寻租的情况,管理部门对公交企业的监管同样存在两种策略:一是严格检查,对公交企业的每次运营活动均进行监管;二是不检查,对公交企业的运营活动监管不进行监管.
此时,管理部门、公交企业形成了一个管理博弈,每一个参与方在进行策略选择时均需考虑到对方的行动策略,而博弈双方的策略选择具有一定的随机性. 因此,可以假定参与者均以某种概率分布选择自身的策略,采用混合策略博弈描述管理部门与常规公交企业之间的均衡策略进行选择.
假定政府管理部门以概率θ(0≤θ≤1)对常规公交企业进行检查,检查所需支付的成本为c1,当发现公交企业存在违规运营行为时,管理部门要对公交企业进行罚款处罚,处罚收益为c2,且管理部门还应承担公交企业违规运营而造成的间接社会损失,其大小为c3,当管理部门检查时发现公交企业不存在违规运营时,应对公交企业进行一定的奖励,其大小为c4.
常规公交企业以概率ω(0≤ω≤1)采取违规运营策略,公交企业正常的收益为e1,当采取违规运营策略时,公交企业可获得额外收益e2.
根据上述条件,该博弈过程的参与者分别是公交企业和管理部门,则博弈者集合可表示为i=1,2,其中i=1代表管理部门、i=2代表公交企业.
每个博弈的参与者所对应的策略空间可表示为Si,i=1,2;其中管理部门的策略空间为S1=S11,S12=检查,不检查,公交企业的策略空间为S2=S21,S22=违规运营,遵规运营;每个参与者所对应的收益函数记为ui,i=1,2.
根据上述假定,可求出不同策略组合下,各参与方的收益函数. 对于博弈参与者而言,其收益值取决于博弈双方的策略组合.
当管理部门采取检查策略,常规公交企业采取违规运营时,管理部门的收益值由3部分组成,即检查所需支付成本c1,对常规公交企业的惩罚收益c2和由于公交企业违规运营而造成的间接社会损失c3;而常规公交企业的收益也包括3部分:公交企业正常收益为e1,额外收益e2,和被管理部门的罚款c2. 则该策略组合下的双方收益可以表示为
| $\left\{ \begin{matrix} {{u}_{1}}{{S}_{11}},{{S}_{21}}=-{{c}_{1}}+{{c}_{2}}-{{c}_{3}}, \\ {{u}_{2}}{{S}_{11}},{{S}_{21}}={{e}_{1}}+{{e}_{2}}-{{c}_{2}}. \\ \end{matrix} \right.$ | (1) |
同理,可得其他策略组合下博弈双方的收益值,汇总管理部门与公交企业之间的收益矩阵,见表 1.
| 表 1 常规公交监管收益矩阵 Table 1 The management payoff matrix of conventional bus |
对于公交企业而言,当管理部门进行检查的时候,公交企业的最优策略应该是遵规运营,即遵规运营的收益值应大于违规运营收益值. 可得
| $-{{c}_{1}}-{{c}_{4}}>-{{c}_{1}}-{{c}_{3}}+{{c}_{2}}.$ | (2) |
整理后可得
| ${{c}_{3}}>{{c}_{4}}+{{c}_{2}}.$ | (3) |
同理,当管理部门采取不检查策略时,公交企业的最优策略是违规运营,显然公交企业的违规运营收益大于遵规运营收益.
而当管理部门遇到公交企业违规运营的情况时,需要对违规公交企业进行罚款处理,只有罚款收益高于违规所得时,才能有效约束公交企业的违规行为,则可知
| ${{c}_{2}}\ge {{e}_{2}}.$ | (4) |
为了便于计算,不妨假设Vθ为管理部门采取检查策略时,公交企业的期望收益,V1-θ为管理部门采取不检查策略时,公交企业的期望收益,Uω为公交企业采取违规运营策略时,管理部门的期望收益,U1-ω为公交企业采取遵规运营策略时,管理部门的期望收益. 根据定义可得
| $\left\{ {\matrix{ \matrix{ {V_\theta } = \omega ( - {c_1} - {c_3} + {c_2}) + \left( {1 - \omega } \right)( - {c_1} - {c_4}) = \hfill \cr \omega ({c_4} + {c_2} - {c_3}) - {c_1} - {c_4}, \hfill \cr} \cr {{V_{1 - \theta }} = \omega ( - {c_3}) + \left( {1 - \omega } \right) \times 0,} \cr \matrix{ {U_\omega } = \theta ({e_1} + {e_2} - {c_2}) + \left( {1 - \theta } \right)({e_1} + {e_2}) = \hfill \cr {e_1} + {e_2} - \theta {c_2}, \hfill \cr} \cr {{U_{1 - \omega }} = \theta ({e_1} + {c_4}) + \left( {1 - \theta } \right){e_1} = \theta {c_4} + {e_1}.} \cr } } \right.$ | (5) |
管理部门和公交企业的期望效用函数分别为V和U. 则可根据期望效用的计算公式得
| $\left\{ \begin{matrix} V=\theta {{V}_{\theta }}+\left( 1-\theta \right){{V}_{1-\theta }}, \\ U=\omega {{U}_{\omega }}+\left( 1-\omega \right){{U}_{1-\omega }}. \\ \end{matrix} \right.$ | (6) |
公交企业在与管理部门博弈的同时,公交企业之间并不是相互独立的[8]. 每个公交企业所选择的策略不仅仅要考虑到管理部门的策略选择,同时也会受到其他公交企业策略选择的影响. 同样,对于管理部门也是如此. 因此,本问题可以看作是在两类有限理性的大群体中随机配对进行博弈的进化博弈问题[9].
根据生物进化复制动态的思想,采用收益较低策略的博弈方往往会改变自身策略,模仿有较高收益策略的对手. 博弈双方采取某种策略动态变化速度为可以用复制动态方程表示,其数学表达式可以写成为
| $\left\{ \begin{matrix} \frac{d\omega }{dt}=\omega ({{U}_{\omega }}-U)=\omega \left( 1-\omega \right)({{e}_{2}}-\theta ({{c}_{2}}+{{c}_{4}})), \\ \frac{d\theta }{dt}=\theta ({{V}_{\theta }}-V)=\theta \left( 1-\theta \right)(\omega ({{c}_{4}}+{{c}_{2}})-{{c}_{1}}-{{c}_{4}}). \\ \end{matrix} \right.~$ | (7) |
根据支付最大化理论,可以得到管理部门与出租车除边界外的唯一Nash均衡,记为(θ*,ω*),即
| $\left\{ \begin{matrix} {{\theta }^{*}}=\frac{{{e}_{2}}}{{{c}_{2}}+{{c}_{4}}}, \\ {{\omega }^{*}}=\frac{{{c}_{1}}+{{c}_{4}}}{{{c}_{2}}+{{c}_{4}}}. \\ \end{matrix} \right.$ | (8) |
系统动力学理论创立于20世纪50年代,是一门用来认识系统问题和解决系统问题的交叉综合学科[10]. 根据前文的博弈分析及模型参数选择,应用系统动力学仿真软件Vensim PLE绘制系统动力学流图,如图 1所示.
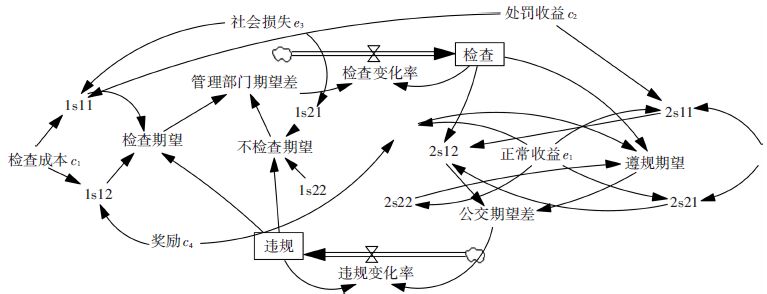
|
图 1 管理部门与公交企业的系统动力学流图 Figure 1 The system dynamics flow between management department and public transport enterprise |
在仿真环境中,假定initial time=0,final time=100,time step=0.5. 博弈双方的模型参数还应该满足一定的逻辑约束,以常规公交企业为例,违规的高收益显然是其违规行为的源动力,故必然有e2>e1,且违规所获得收益应明显小于对社会造成的整体损失,则e2+e1<c3. 因此模型参数初始化如下:检查成本c1=0.5,罚款收益c2=3,社会期望损失c3=5,遵规奖励c4=1,公交企业正常收益e1=1,违规额外收益e2=2.
根据前文分析,管理部门与公交企业之间存在复杂的博弈关系,但经过一段时间的博弈行为之后,双方的策略选择会逐渐趋于一个稳定点,但在传统博弈论中并没有解释如何达到稳定均衡的问题.
根据下式可计算出博弈过程除边界外唯一的纳什均衡,即
| $\left\{ \begin{matrix} {{\theta }^{*}}=\frac{{{e}_{2}}}{{{c}_{2}}+{{c}_{4}}}=\frac{2}{3+1}=0.5, \\ {{\omega }^{*}}=\frac{{{c}_{1}}+{{c}_{4}}}{{{c}_{2}}+{{c}_{4}}}=\frac{0.5+1}{3+1}=0.375. \\ \end{matrix} \right.$ |
由定性分析可知,当管理部门采取检查策略时,常规公交企业的最佳策略显然是遵规运营,即策略1:θ=1,ω=0,当管理部门采取不检查策略时,对于常规公交企业而言,其最佳策略应为违规运营,即策略2:θ=0,ω=1.
而对于边界点θ=0,ω=0或者θ=1,ω=1时,显然与常规策略选择相悖,对比分析策略3:θ=0,ω=0.01;策略4:θ=1,ω=0.99. 运行仿真环境,策略对比如图 2所示.
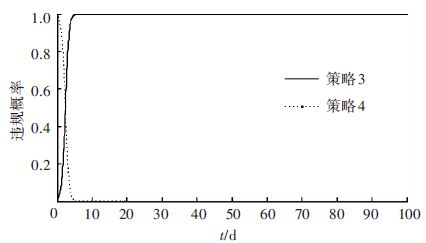
|
图 2 博弈双方不同策略初值对稳定态的影响 Figure 2 The different initials influence on the steady-state |
从式(7)可以得知,策略1和策略2显然均处于稳定状态,从图 2可以看出,策略3和策略4是一种临界稳定,但经过博弈后,其策略迅速调整,这是因为在该博弈过程中,常规公交企业之间存在着新策略的学习,一旦某一参与者的策略可以获得较大收益,则原有的博弈平衡被打破,其余参与者能够迅速调整自身策略,以获取更大收益,从而达到新的稳定状态,即管理部门的检查策略与常规公交企业遵规运营策略组合,或者管理部门的不检查策略与常规公交企业违规运营策略组合.
在实际博弈过程中,参与双方的策略选择具有随机性,假定当博弈过程中一方的初始策略为纳什均衡,而另一方随机的以(0,1)中任何一个非纳什均衡比例参与博弈. 本文拟定管理部门以纳什均衡θ*=0.5作为策略选择初始值,分别对比常规公交企业以ω1=0.3,ω2=0.5,如图 3所示,可以看出,当博弈双方的策略初值随机选择时,除边界值与纳什均衡值外,其余取值都使得博弈双方在策略选择上存在一定波动,且随着策略初值与纳什均衡值差值的增大,波动幅值逐渐增大,波动的频率呈现衰减,直至波动达到最大值,使得博弈过程变得难以控制.
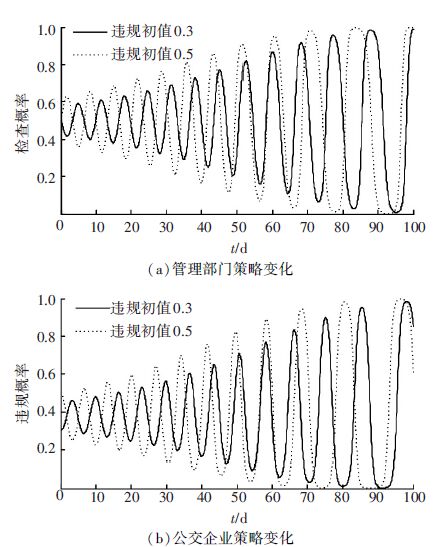
|
图 3 不同策略初值条件下双方策略的变化曲线 Figure 3 Both strategies changing curve with different initials |
为了提高常规公交的服务水平,保证公共交通在居民出行中的主体地位,管理部门需要采取各种切实可行的策略对公交企业的违规行为进行监管,经济策略是比较常用的管理策略之一.
3.1 改变惩罚收益在经济策略里,最常用的策略就是增加对违规企业的惩罚收益. 假设在初始模型仿真的第10天加大对违规企业的惩罚力度,即违规收益c2取值由3变为6,则博弈双方策略变化曲线如图 4所示.
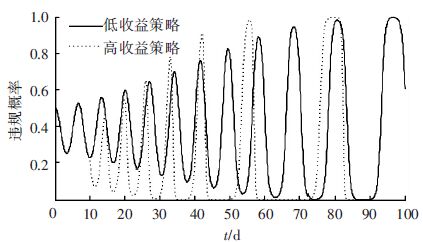
|
图 4 不同惩罚收益条件下违规策略的变化曲线 Figure 4 The illegal strategy changing curve with different punishment |
从图 4可以看出,在第10天增大了对违规行为的惩罚力度,使得违规概率的波动频率在短期内呈现一定程度的减小,但很快又达到新的振荡状态,即仅仅通过增加违规罚款的方式并不能有效约束公交企业的违规行为.
3.2 信息延迟博弈建模及仿真假定在实际情况下博弈参与者对于检查及策略学习信息的获取具有一定延迟. 假定信息延迟量为5,在其他参数不变的条件下,博弈仿真结果如图 5所示. 结果表明,随着时间的增加,双方策略呈现出较大范围的波动,但波动频率明显降低,很难达到均衡值. 因此,需要有效地管理策略来保证博弈过程快速达到均衡点或者有效缩小博弈过程的波动范围.
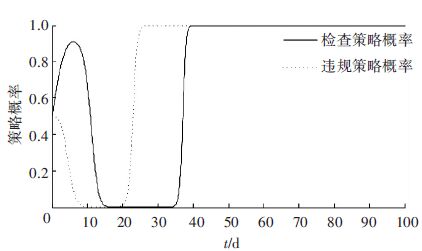
|
图 5 延迟环节下双方策略变化曲线 Figure 5 Both strategies changing in delayed part |
通过前文中静态管理策略的分析可以看出,简单的增大惩罚收益并不能有效地抑制违规波动,而且会对管理策略的实施带来一定的影响,使得管理部门对于管理策略的选择更加困难. 因此,本文考虑公交企业违规惩罚力度与违法概率相关时的动态管理策略.
假设管理部门采取检查策略时,公交企业分别采取违规运营和遵规运营策略的收益差主要为额外收益e2. 因此,假设对公交企业的惩罚收益与公交企业违规概率间时正相关的,则可以用公交企业违规概率ω来描述公交企业违规收益,即当公交企业采取违规运营,管理部门采取检查策略时,公交企业的额外收益e2由原来的常数变成了违规运营概率ω的函数,其函数关系可以采用线性关系式
| ${{e}_{2}}=m\times \left( 1-\omega \right),$ | (9) |
式中m为管理部门对于公交企业违规运营的最大惩罚收益.
根据前文假设,分别取m=2和m=4,对比分析博弈双方策略变化,如图 6、7所示.
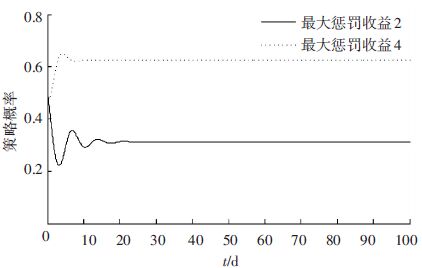
|
图 6 不同最大惩罚收益条件下管理部门策略变化 Figure 6 The management strategy changing with different punishment |
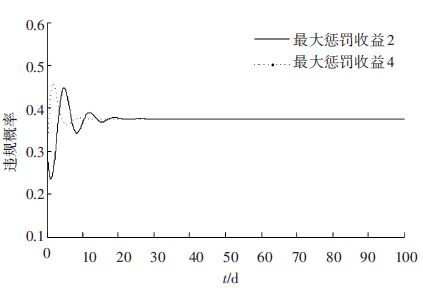
|
图 7 不同最大惩罚收益条件下公交企业违规策略变化 Figure 7 The bus strategy changing with different maximum punishment |
从图 6、7可以看出,当采用动态惩罚策略时,即违规运营额外收益值与违规运营概率相关时,此时博弈双方达到博弈均衡的时间可以得到有效缩短,同时也可以有效抑制博弈过程的波动性. 此外,在动态惩罚策略下,随着m值的增大,博弈双方达到博弈均衡的时间将缩短,波动的幅值也减小. 管理部门的检查策略的均衡值则呈现增加的趋势,即需要管理部门加大检查力度才能保证管理效果. 在m=2时,双方策略的博弈演变过程如图 8所示.
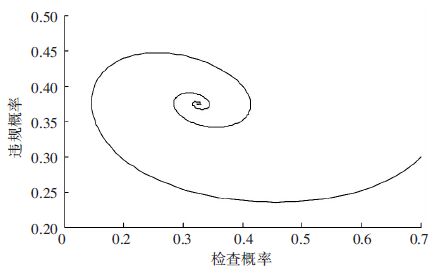
|
图 8 m=2时博弈双方策略演变曲线 Figure 8 The strategy game evolution in the condition of m=2 |
从图 8可以看出,动态惩罚策略条件下,双方策略博弈曲线很快收敛到稳定值. 双方策略的波动得到了很好的抑制,即缩短了收敛时间,取得了较好的管理效果.
4 结 论1) 通过对公共交通企业和管理部门在实际中的策略选择问题进行研究,以策略选择概率为研究对象,分析了博弈双方在不同策略下的演化过程. 考虑了博弈参与方的收益矩阵,建立了城市公共交通企业和管理部门间的博弈模型来描述城市公共交通管理过程中的博弈关系,给出了在有限理性条件下各方策略变化过程的求解方程.
2) 根据复制动态方程,给出了双方策略变化的解,参照博弈模型建立了基于系统动力学的仿真模型,并进行了不同惩罚策略的仿真分析.
3) 当管理部门采用静态惩罚策略时,纳什均衡值是双方除边界值外的唯一稳定解,其他初始值均使得博弈过程不存在演化稳定策略,且波动的峰值随着初始值与纳什均衡值间差值的增大而增大.
4) 当采用动态惩罚策略时,博弈过程存在明显的演化稳定策略,能够较好地抑制博弈过程中的波动状态,随着最大惩罚收益的增大,博弈波动过程的收敛时间和波动幅值都减小.
| [1] |
DEFLORIO F P. Simulation of requests in demand responsive transport systems[J].
Intelligent Transport Systems, IET,2011, 5 (3) : 159-167.
DOI: 10.1049/iet-its.2010.0026 ( 0) 0)
|
| [2] |
LI X, QUADRIFOGLIO L. Feeder transit services: choosing between fixed and demand responsive policy[J].
Transportation Research Part C: Emerging Technologies,2010, 18 (5) : 770-780.
DOI: 10.1016/j.trc.2009.05.015 ( 0) 0)
|
| [3] |
陈宽民, 罗小强. 城市快速轨道交通合理票价的博弈分析[J].
长安大学学报(自然科学版),2005, 25 (4) : 52-55.
CHEN Kuanmin, LUO Xiaoqiang. Game-theory of reasonable ticket price for urban railway transport[J]. Journal of Chang’an University(Natural Science Edition),2005, 25 (4) : 52-55. (  0) 0)
|
| [4] |
王炜, 杨新苗, 陈学武.
城市公共交通系统规划方法与管理技术[M]. 北京: 科学出版社, 2006 : 165 -170.
WANG Wei, YANG Xinmiao, CHEN Xuewu. Urban public transport system planning and management technology[M]. Beijing: Science Press, 2006 : 165 -170. (  0) 0)
|
| [5] |
刘惠玲, 关伟. 基于系统动力学的城市公交系统模型[J].
城市公共交通,2007 (6) : 24-28.
LIU Huiling, GUAN Wei. Urban public transportation system model based on system dynamics[J]. Urban Public Transport,2007 (6) : 24-28. (  0) 0)
|
| [6] |
唐旭南, 张秀媛, 孙浩. 城市常规公交子系统能耗模型研究[J].
交通运输系统工程与信息,2012, 12 (1) : 160-165.
TANG Xunan, ZHANG Xiuyuan, SUN Hao. Energy consumption models for urban bus transport[J]. Journal of Transportation Systems Engineering and Information Technology,2012, 12 (1) : 160-165. (  0) 0)
|
| [7] |
韩烈, 张宁. 单起点多讫点公共交通系统早高峰乘车均衡性质研究[J].
系统工程理论与实践,2014, 34 (7) : 1847-1856.
HAN Lie, ZHANG Ning. Equilibrium properties of the morning peak-period commuting in a one-to-many mass transit system[J]. Systems Engineering—Theory & Practice,2014, 34 (7) : 1847-1856. (  0) 0)
|
| [8] |
孙广林, 王健, 姜成福. 城市公交价格联动策略的演化博弈[J].
交通运输系统工程与信息,2013, 13 (4) : 164-170.
SUN Guanglin, WANG Jian, JIANG Chengfu. Evolutionary game of urban public traffic pricing linkage strategy[J]. Journal of Transportation Systems Engineering and Information Technology,2013, 13 (4) : 164-170. (  0) 0)
|
| [9] |
陈荣钦, 林君焕, 陈月芬. 一种基于Q学习的有限理性博弈模型及其应用[J].
系统仿真技术,2013, 10 (3) : 203-210.
CHEN Rongqin, LIN Junhuan, CHEN Yuefen. A limited rational game model based on Q-learning and its application[J]. System Simulation Technology,2013, 10 (3) : 203-210. (  0) 0)
|
| [10] |
宋成举, 张亚平, 姜莉. 城市公共交通系统发展策略的系统动力学建模与仿真[J].
黑龙江工程学院学报(自然科学版),2014, 28 (1) : 15-19.
SONG Chengju, ZHANG Yaping, JIANG Li. Modeling and simulation for the development strategy of urban public transit system using system dynamics[J]. Journal of Heilongjiang Institute of Technology,2014, 28 (1) : 15-19. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


