2. 汽车动态模拟国家重点实验室(吉林大学),长春 130022
2. State Key Laboratory of Automotive Simulation and Control (Jilin University),Changchun 130022, China
如今城市道路交通系统越发拥挤,不仅影响人们出行的可达性,同时威胁到了城市经济与生态的可持续发展. 行程时间作为表征交通运行状况的一项重要指标,准确地估计能够为交通管理人员及出行者带来极大的便利. 有许多方法可用来采集行程时间数据,如线圈检测器、自动车辆识别技术等. 但是,路网中这些检测器的数量是有限的,因此不能代表整个网络的运行状态[1]. 利用浮动车数据(简称FCD)进行行程时间估计是近些年的研究热点. 浮动车数据覆盖面广,采样时间间隔较长(30~120 s),两探测点间相距较远,这对行程时间的准确估计是较大的挑战. 目前低频FCD的研究大多是基于路段的行程时间估计[2-5]. 所提出的方法主要分两步进行:第1步每个FCD观测被分解到各个遍历路段上[3-4];第2步是行程时间计算,可以是平均行程时间的经验算法[2],也可以是基于概率分布估计的复杂模型算法[3, 6]. 实证研究表明行程时间与路段有很大的关系[7-8],然而大多数的研究都假设路段行程时间是互相独立的[9-10]. 这会导致路径水平上的行程时间估计有所偏差. 鉴于以上研究的不足,本文提出一种利用低频FCD数据直接进行路径行程时间估计的方法,能够有效提高估计精度.
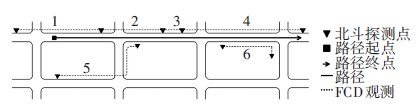
1 低频浮动车数据行程时间估计的误差分析路径定义为起终点之间的一系列路段及交叉口. 浮动车数据的探测点通常与路段或路径的起终点不吻合,因此,在使用FCD进行行程时间估计时存在一些潜在误差. 本文所述的一个观测由两个探测点所确定. 图 1为几种产生误差的FCD观测示例.
|
图 1 地图匹配后的FCD观测示例 Figure 1 Examples of FCD observations after map-matching |
以下是几种常见的误差:1)路径上浮动车观测的不完整覆盖. FCD的观测可能只覆盖路径的一部分[11]. 路径上的行程时间不可知,需要进行推测,由此导致误差的产生; 2)基于时间的抽样. 车辆轨迹的样本通常是由时间触发的,如果车速很低,连续探测点之间的距离就很短,该部分的FCD探测点也较多[12]. 在行程时间估计的过程中需要考虑这个因素以减少误差; 3)邻接路网的影响. FCD的观测可能一部分覆盖到路径上面,其余部分在邻接路段上[13],例如图 1的观测1和4~6,此时行程时间T不能够进行准确地分配,误差也由此产生; 4)路径上探测点的非均匀覆盖. 车辆可能经由支路进入或离开街道[14],如果行车速度在路径上不均匀,当所有观测赋予一样的权重时,行程时间估计就会产生误差; 5)路径进入时间未知. FCD观测的起始点与路径的起始点不吻合,确切的进入时间就不可知[15-16],如果推测不准确就会有相应的误差.
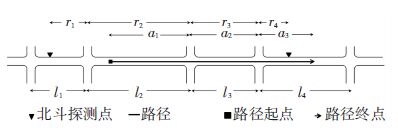
2 路径行程时间估计及修正 2.1 路径行程时间估计方法路径行程时间可通过两种方法估计:路段行程时间的聚合估计或对路径的直接估计. 无论采用哪种方法,都必须进行FCD数据的预处理. 经过地图匹配和路径选择,车辆每一对连续的探测点数据都会返回路段序列,以及车辆在第一个路段和最后一个路段上投影探测点的偏差. 本文定义τi为第i个行程时间观测值;si为第i个观测值的时间戳;ρik为观测i的长度与路段k的长度的比值;αk为路径覆盖路段k的长度与路段k的长度的比值;βik为路径上观测i的长度与路段k的长度的比值;lk为路段k的长度. 其中:ρ1=r1/l1,ρ2=r2/l2,ρ3=r3/l3,ρ4=r4/l4,α1=0,α2=a1/l2,α3=a2/l3,α4=a3/l4,β1=0,β2=a1/l2,β3=r3/l3,β4=r4/l4. 变量说明见图 2.
|
图 2 变量r、a和l的说明图示 Figure 2 Notation examples of r,a and l |
基于路段的行程时间估计主要有两步:将行程时间分配到路段上; 估计每个路段的行程时间.
1) 行程时间分配. 观测的行程时间τi按距离成比例地分配到所遍历的路段上,计算公式为
| ${{\tau }_{ik}}=\frac{{{\rho }_{ik}}{{l}_{k}}}{{{\sum }_{k}}{{\rho }_{ik}}{{l}_{k}}{{\tau }_{i}}}.~$ | (1) |
式中τik为第i个行程时间观测值分配到路段k上的行程时间. 使用预设的路段行程时间tk0代替路段长度lk,这个时间可以是自由流时的路段行程时间.
2) 聚合. 对于一些观测来说,它们与路段并不是完全重叠,τik要通过系数1/ρik比例扩大到路段上去,计算公式为
| ${{t}_{ik}}=\frac{1}{{{\rho }_{ik}}}{{\tau }_{ik}}.$ | (2) |
式中tik为第i个行程时间观测值成比例扩大到路段k上的行程时间. 这种比例扩大假设行车速度沿着路段是均匀的.
观测与路段重叠越小数据越不可信,每个路段都根据其覆盖的部分赋予相应的权重,平均路段行程时间t-k可由所有观测加权平均计算得到,即
| ${{\bar{t}}_{k}}=\frac{{{\sum }_{i}}{{\rho }_{ik}}{{t}_{ik}}}{{{\sum }_{i}}{{\rho }_{ik}}}.$ | (3) |
3)路径平均行程时间. 为了估计路径平均行程时间,将路径上路段的平均行程时间加和,且路段行程时间根据重叠长度成比例地分配,计算公式为
| $\bar{T}={{\sum }_{k}}{{\alpha }_{k}}{{\bar{t}}_{k}},$ | (4) |
式中T为路径平均行程时间.
2.1.2 基于路径的基线行程时间估计本文基线行程时间指基于路径的且未经修正的行程时间. 基于路段的行程时间方法产生一个单值,而基于路径行程的时间具有分布特性,本文将路径作为一个虚拟路段,直接估计路径行程时间. 类比基于路段的行程时间估计方法,观测的行程时间首先在邻接路网和路径之间进行分割,即
| ${{\tau }^{{{R}_{i}}}}=\frac{{{\sum }_{k}}{{\beta }_{ik}}{{l}_{k}}}{{{\sum }_{k}}{{\rho }_{ik}}{{l}_{k}}}{{\tau }^{_{i}}}.~$ | (5) |
式中τRi(R—route,路径)为分配于路径上的行程时间. 再根据覆盖到路段上的距离分数按比例放大到整个路径上去,即
| ${{T}_{i}}={{\omega }_{i}}{{\tau }_{i}}^{R},$ | (6) |
| ${{\omega }_{i}}=\frac{{{\sum }_{k}}{{\alpha }_{k}}{{l}_{k}}}{{{\sum }_{k}}{{\beta }_{ik}}{{l}_{k}}}.$ | (7) |
式中Ti为比例放大后的路径行程时间.
每个观测都根据覆盖路径的分数1/ωi赋予相应的权重. 路径行程时间分布的统计特性可由加权的观测得到. 例如,平均路径行程时间为
| $\bar{T}={{\sum }_{i}}\frac{{{T}_{i}}}{{{\omega }_{i}}}/{{\sum }_{i}}\frac{1}{{{\omega }_{i}}}.$ | (8) |
1) 时间分配. 本文采用预设行程时间tk0,该值可由自由流速度或路段水平上的行程时间估计得到,这样可使估计的每一步更为精准. 首先,观测的行程时间基于时间而非距离,以分配比例φi分配于路径上的行程时间为
| ${{\tau }_{i}}^{R}={{\varphi }_{i}}{{\tau }_{i}},$ | (9) |
| ${{\varphi }_{i}}=\frac{{{\sum }_{k}}{{\beta }_{ik}}{{t}^{0}}_{k}}{{{\sum }_{k}}{{\rho }_{ik}}{{t}^{0}}_{k}}.$ | (10) |
通过以上计算能减少来自支路的影响所引起的误差. τiR可以根据重叠部分的平均速度与整个路径平均速度的比率ηi按比例放大到路径上去,即
| ${{T}_{i}}={{\eta }_{i}}{{\tau }_{i}}^{R},$ | (11) |
| ${{\eta }_{i}}=\left( \left( \frac{{{\sum }_{k}}{{\beta }_{ik}}{{l}_{k}}}{{{\sum }_{k}}{{\beta }_{ik}}{{t}_{k}}^{0}} \right)/\left( \frac{{{\sum }_{k}}{{\alpha }_{k}}{{l}_{k}}}{{{\sum }_{k}}{{\alpha }_{k}}{{t}_{k}}^{0}{{\omega }_{i}}} \right) \right)=\frac{{{\sum }_{k}}{{\alpha }_{k}}{{t}_{k}}^{0}}{{{\sum }_{k}}{{\beta }_{ik}}{{t}_{k}}^{0}.~}$ | (12) |
通过这个修正可以减少路径不完整覆盖的影响(误差1). 如果车辆的行驶轨迹是根据时间采样,探测点之间的短距离表明速度低. 因此,用1/ωi对观测赋权重会使行程时间估计的值变小(误差2). 为了减少这个误差,这里用1/ηi对观测赋权重,即重叠部分的行程时间与整个路径行程时间的比率. 估计的平均路径行程时间为
| $\bar{T}={{\sum }_{i}}\frac{{{T}_{i}}}{{{\eta }_{i}}}/{{\sum }_{i}}\frac{1}{{{\eta }_{i}}}.$ | (13) |
2)邻接网络覆盖阈值. 为了减少支路对路径行程时间的影响,这里采用φi,即路径上的行程时间与覆盖观测的总行程时间的比率. φi小于定义的阈值φmin(比如0.75)的观测被排除(误差3).
3)FCD的串联估计. 车辆沿着路径报告一系列的探测点(例如:图 1的观测1~4). 考虑车辆在路径上的几个观测作为一个片段进行行程时间的估计更为合理. 用这个方法对行程时间进行串联降低了几种误差的影响:改善了路径覆盖率(误差1),减少了基于时间采样时在低速部分产生较多探测点带来的影响(误差2),并且能够使路径进入时间的推测更加合理(误差5).
串联遵循以下步骤:1)将同一个路线的观测组织在一起作为一个轨迹;2)令轨迹匹配路径,即选择一组轨迹子集来覆盖路径;3)将子集的观测进行合并,即子集的第1个(最后1个)时间戳成为观测的第1个(最后一个)时间戳;子集的第1个(最后1个)偏差成为观测的第1个(最后1个)偏差.
4)路径进入时间外推法. 为了推测(假想的)路径进入时间,减少误差5,观测i的第1个时间戳si外推si′为
| ${{s}_{i}}^{\prime }={{s}_{i}}+{{t}_{i}}^{(1)}-{{t}_{i}}^{(2)}.$ | (14) |
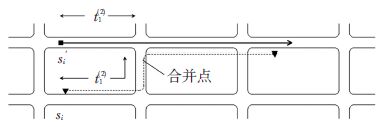
式中ti(1)为第1个探测点与观测进入路径时的点之间的距离,ti(2)为路径进入点和观测加入点之间假想的行程时间,如见图 3所示.
|
图 3 进入时间外推法示意 Figure 3 Diagram of route entry time extrapolation |
ti(1)和ti(2)可以基于路段行程时间或基于观测本身进行估计,计算公式为
| ${{t}_{i}}^{(1)}={{\tau }_{i}}\left( {{\sum }_{m\in M}}{{\rho }_{im}}{{l}_{m}} \right)/\left( {{\sum }_{k}}{{\rho }_{ik}}{{l}_{k}} \right),$ | (15) |
| ${{t}_{i}}^{(2)}=({{\sum }_{n\in N}}{{\alpha }_{n}}{{l}_{n}})/{{\bar{v}}_{i}}.$ | (16) |
式中:M为进入路径之前未覆盖路段的集合,N为路径开始与合并点之间路段的集合,v-i为观测i的平均速度,计算公式为
| ${{{\bar{v}}}_{i}}=({{\sum }_{k}}{{\rho }_{ik}}{{l}_{k}})/{{\tau }_{i}}.$ | (17) |
5)基于路段数的权重赋值. 路径的不均匀覆盖(误差4)意味着FCD不能成为路径行程时间有代表性的样本. 为了减少此误差,每个观测应根据覆盖路段平均观测数的倒数赋予相应的权重,即
| ${{\lambda }_{i}}={{\sum }_{k}}{{\beta }_{ik}}{{t}^{0}}_{k}{{\sum }_{k}}{{\beta }_{ik}}{{t}^{0}}_{k}{{C}_{k}}.$ | (18) |
式中Ck为(部分或全部)覆盖路段k上的观测数.
权重λi乘以1/ηi得到每个观测的最终权重. 因此,平均路径行程时间为
| $T-={{\sum }_{i}}{{\eta }_{i}}{{T}_{i}}{{\lambda }_{i}}{{\sum }_{i}}{{\eta }_{i}}{{\lambda }_{i}}.$ | (19) |
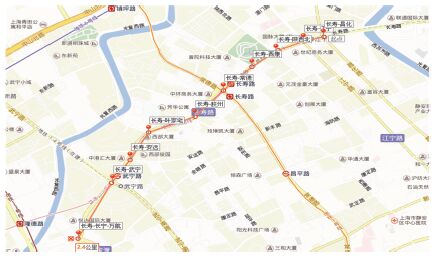
选取上海市长寿路的部分路段(记为路径A)进行行程时间估计. 路径A长2.4 km,限速50 km/h,共有10个交叉口,图 4为实验路段示意图.
|
图 4 实验路段示意 Figure 4 Test section schematic |
FCD数据来自1 500辆出租车,每个出租车每隔2 min都报告其位置(经度和纬度)、时间戳及车辆的ID.
路径A上装有车牌识别(简称LPR)装置,LPR数据可以用来提供直接的行程时间估计,用作本文路径行程时间估计的对比项. 数据收集于2015年5—7月份周一至周四的6:00—20:00时.
3.2 结果分析利用上文提到的估计方法和修正方法对行程时间进行估计与修正. 为了验证所提出方法的有效性,选择一种已有且适用低频浮动车的改进内插值算法进行对比分析[11].表 1为所有误差均修正了的行程时间估计方法和改进内插值估计方法的平均绝对相对误差EMAR、平均绝对误差EMR和标准差DS的统计.
| 表 1 两种方法的行程时间估计误差统计 Table 1 Travel time estimation error statistics of two methods |
从表 1可以看出:相对于改进内插值方法,本文所提出的方法估计值更接近实际,具有较高的估计精度. 各误差提高精度的平均值为9.5%. 为了验证所提出方法的适应性,由FCD方法估计的路段行程时间与LPR方法进行相似性分析. 由LPR和FCD以15 min的间隔分组(从6:00—20:00时共N=36个间隔),从而计算每个时间间隔的行程时间数据. 并且利用均方根差(简称RMSE)计算LPR和FCD之间的相似性,RMSE计算公式为
| ${{R}_{MSE}}=\sqrt{\frac{{{\sum }_{n}}{{({{S}_{n}}^{LPR}-{{S}_{n}}^{FCD})}^{2}}}{N}}.$ | (20) |
式中SnLPR为基于LPR的行程时间统计量,SnFCD为基于FCD的行程时间统计量,n=1,2,…,N.
表 2为使用不同的估计方法和误差修正方法所得不同分位数的RMSE值,最后一行展示了所有误差均被修正的基于路径的RMSE结果. 所有方法的RMSE在0.23~0.29之间变化.
| 表 2 FCD与LPR的RMSE结果 Table 2 RMSE results of FCD and LPR |
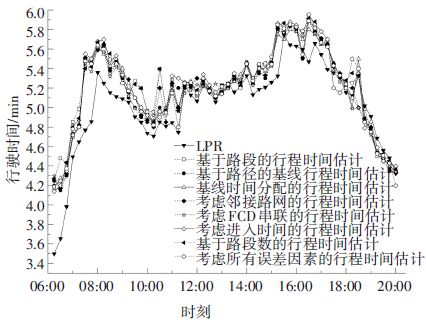
图 5展示了路径A一天中各个方法下的平均行程时间示意图,包括基于LPR的行程时间估计,基于路段的行程时间估计以及各种误差修正下基于FCD的路径行程时间估计. 可以看出,各种方法估计的行程时间有着相似的趋势,一天之中的早晚高峰行程时间均高于其他时间,这与城市道路交通一天之内的变化情况是相符的. 中午和傍晚FCD估计方法与LPR行程时间数据有较好的匹配度,然而在其余时间有着过高的估计.
|
图 5 基于FCD和LPR的平均路径行程时间对比 Figure 5 Mean route travel time contrast based on FCD estimation and LPR data |
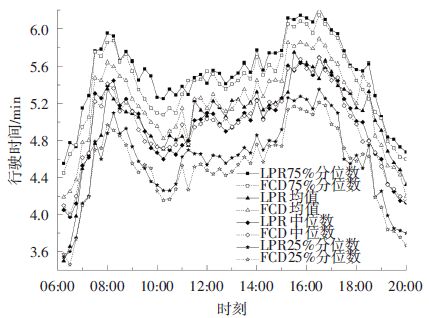
基于路径的行程时间估计方法的平均值与基于路段的估计方法有着相似的效果,而基于路径方法的主要优势在于有着估计其他统计量的能力. 图 6展示了一天之中行程时间分布的中位数,25%分位数和75%分位数.
|
图 6 FCD和LPR各统计量对比曲线 Figure 6 Statistical variables comparison curve of route travel time according to FCD estimation and LPR data |
从表 2的RMSE结果可以看出基于FCD的方法较好地估计了各个百分位数. 这些百分位数RMSE值表明考虑时间分配和FCD串联是改善行程时间估计精度最大的两个影响因素. 因此在条件有限的情况下,可优先用这两种方法对行程时间进行估计.
4 结 论1) 针对低频浮动车数据不完整覆盖、不均匀覆盖、邻接网络部分覆盖、样本代表性差等误差来源进行分析,并提出了5个模型来减少这些误差的影响.
2) 选取上海市长寿路部分路段进行实例分析,分别使用FCD和LPR对平均行程时间及其分布的中位数、25%分位数及75%分位数进行估计,与改进内插值方法对比并利用RMSE进行相似性分析,结果表明平均估计精度提高了9.5%,所有误差均修正了的行程时间估计的均方根误差较小,且估计的各百分位数与车牌识别方法有较高的匹配度,RMSE分别为0.24、0.15、0.15和0.26,等于或优于其他方法的RMSE.
3) 利用低频浮动车数据进行行程时间估计可以辅助固定检测器在更大的路网上完成交通状态的监测,并且可以在更大范围上评估拥挤水平和行程时间的可变性,还可以直接利用估计的行程时间,进行拥挤系数的计算,从而制定有效的拥挤收费策略.
| [1] |
李慧兵, 杨晓光, 罗莉华. 路段行程时间估计的浮动车数据挖掘方法[J].
交通运输工程学报,2014, 14 (6) : 100-109.
LI Huibing, YANG Xiaoguang, LUO Lihua. Mining method of floating car data based on link travel time estimation[J]. Journal of Traffic and Transportation Engineering,2014, 14 (6) : 100-109. (  0) 0)
|
| [2] |
QUDDUS M, WASHINGTON S. Shortest path and vehicle trajectory aided map-matching for low frequency GPS data[J].
Transportation Research Part C:Emerging Technologies,2015, 55 : 328-339.
DOI: 10.1016/j.trc.2015.02.017 ( 0) 0)
|
| [3] |
HOFLEITNER A, HERRING R, ABBEEL P, et al. Learning the dynamics of arterial traffic from probe data using a dynamic Bayesian network[J].
IEEE Transactions on Intelligent Transportation Systems,2012, 13 (4) : 1679-1693.
DOI: 10.1109/TITS.2012.2200474 ( 0) 0)
|
| [4] |
GONG Q, ADAMS T M, WANG X B, et al. Estimating link travel time with sparse GPS data on highway corridors[J].
Transportation Research Record,2015, 2477 : 7-17.
DOI: 10.3141/2477-02 ( 0) 0)
|
| [5] |
HELLINGA B, IZADPANAH P, TAKADA H, et al. Decomposing travel times measured by probe-based traffic monitoring systems to individual road segments[J].
Transportation Research Part C,2008, 16 (6) : 768-782.
DOI: 10.1016/j.trc.2008.04.002 ( 0) 0)
|
| [6] |
WESTGATE B S, WOODARD D B, MATTESON D S, et al. Travel time estimation for ambulances using Bayesian data augmentation[J].
Annals of Applied Statistics,2013, 7 (2) : 1139-1161.
DOI: 10.1214/13-AOAS626 ( 0) 0)
|
| [7] |
ZHENG F F, ZUYLEN H V. Urban link travel time estimation based on sparse probe data[J].
Transportation Research Part C,2013, 31 : 145-157.
DOI: 10.1016/j.trc.2012.04.007 ( 0) 0)
|
| [8] |
YUAN Y, VAN LINT H, VAN WAGENINGEN-KESSELS F, et al. Network-wide traffic state estimation using loop detector and floating car data[J].
Journal of Intelligent Transportation Systems,2014, 18 (1) : 41-50.
DOI: 10.1080/15472450.2013.773225 ( 0) 0)
|
| [9] |
RAMEZANI M, GEROLIMINIS N. On the estimation of arterial route travel time distribution with Markov chains[J].
Transportation Research Part B,2012, 46 (10) : 1576-1590.
DOI: 10.1016/j.trb.2012.08.004 ( 0) 0)
|
| [10] |
JENELIUS E, KOUTSOPOULOS H N. Travel time estimation for urban road networks using low frequency probe vehicle data[J].
Transportation Research Part B:Methodological,2013, 53 : 64-81.
DOI: 10.3969/j.issn.1000-565X.2015.10.005 ( 0) 0)
|
| [11] |
王志建, 马超锋, 李梁. 低频GPS数据和交叉口延误下的行程时间估计[J].
西南交通大学学报,2015, 50 (2) : 361-367.
WANG Zhijian, MA Chaofeng, LI Liang. Link travel time estimation for urban roads using low frequency GPS data and intersection delay[J]. Journal of Southwest Jiaotong University,2015, 50 (2) : 361-367. (  0) 0)
|
| [12] |
姜桂艳, 常安德, 牛世峰. 基于车牌识别数据的交通拥堵识别方法[J].
哈尔滨工业大学学报,2011, 43 (4) : 131-135.
JIANG Guiyan, CHANG Ande, NIU Shifeng. Traffic congestion identification method based on license plate recognition data[J]. Journal of Harbin Institute of Technology,2011, 43 (4) : 131-135. (  0) 0)
|
| [13] |
JENELIUS E, KOUTSOPOULOS H N. Probe vehicle data sampled by time or space:consistent travel time allocation and estimation[J].
Transportation Research Part B:Methodological,2015, 71 : 120-137.
DOI: 10.1016/j.trb.2014.10.008 ( 0) 0)
|
| [14] |
李宇光.海量低频浮动车数据道路匹配及行程时间估算[D].武汉:武汉大学,2013.
LI Yuguang.Huge-volume low-frequency floating car date map-matching and travel time estimation[D].Wuhan:Wuhan University,2013. (  0) 0)
|
| [15] |
GUESSOUS Y, ARON M, BHOURI N, et al. Estimating travel time distribution under different traffic conditions[J].
Transportation Research Procedia,2014, 3 : 339-348.
DOI: 10.1016/j.trpro.2014.10.014 ( 0) 0)
|
| [16] |
ZHAN X Y, HASAN S, UKKUSURI S V, et al. Urban link travel time estimation using large-scale taxi data with partial information[J].
Transportation Research Part C:Emerging Technologies,2013, 33 : 37-49.
DOI: 10.1016/j.trc.2013.04.001 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


