2. 现代城市交通技术江苏高校协同创新中心,南京210096 ;
3. 公安部交通管理科研所,江苏 无锡214151
2. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies,Nanjing 210096,China ;
3. National Road Traffic Management Engineering Technology Research Center,Wuxi 214151,Jiangsu,China
目前交通事件已成为导致城市快速路交通拥堵,降低路网运行效率的主要原因之一,一旦发生,极易形成道路通行能力的瓶颈,产生车辆拥挤排队现象. 如事件未得到及时处理,交通拥堵极可能会扩散并导致路网的大面积交通拥堵,甚至是交通瘫痪. 因此,研究交通事件对城市快速路的影响是十分必要的. 在现有的交通事件影响研究[1-5] 中,大多数以高速公路为研究对象,而由于快速路的出入口匝道间距较小,与普通城市道路联系较为紧密,其与高速公路的路网结构和交通流特性均有较大不同,因此高速公路的事件影响扩散机理并不适用于城市快速路. 因此,本文拟基于MCTM模型,考虑交通流的亚稳态现象及交通事件的影响,构建事件影响下的快速路交通流模型,从而揭示因事件引发的快速路交通拥堵的形成与扩散机理,确定交通事件在此路网条件下的影响范围,为城市交通管理部门提供科学的理论和技术支持.
1 MCTM模型 1.1 MCTM路段模型MCTM模型(modified cell transmission model)是Muñoz等[6-7]在传统CTM模型[8-9]的基础上改进得到的,其避免了原始模型中元胞长度必须均一化的限制,可灵活按照路段的几何特征来划分元胞,更便于为城市路网建模. 该模型将元胞内的交通流密度作为特征参数来描述离散化后的流量守恒式,即
| ${{\rho }_{i}}\left( k+1 \right)\text{=}{{\rho }_{i}}\left( k \right)+\frac{\Delta t}{{{l}_{i}}}\left( {{q}_{i,\text{in}}}\left( k \right)-{{q}_{i,\text{out}}}\left( k \right) \right).$ | (1) |
式中:ρi(k+1)为k+1时段元胞i的车流密度;ρi(k)为k时段元胞i的车流密度;Δt为时间步长;li为元胞i的长度,为避免出现元胞内车辆为负或车流密度大于堵塞密度的情况,该值应不小于Δt内车流自由走行的距离;qi,in(k),qi,out(k)分别为k时段单位时间内流入和流出元胞i的车流量.
依据元胞间的连接方式,可分别计算k时段元胞的驶入流量qi,in(k)和驶出流量qi,out(k),进而得到时段内各元胞的车流密度ρi(k),并将其与该元胞的临界密度ρi,o(k)进行对比得出元胞内的车流状态. 当ρi(k)<ρi,o(k)时,则k时段元胞i处于自由流状态;当ρi(k)≥ρi,o(k)时,则k时段元胞处于拥挤流. (k,k+1)时段驶入元胞i的车辆数为
| ${{y}_{i}}\left( k \right)={{q}_{i}}\left( k \right)\Delta t=\min \left[ {{S}_{i-1}}\left( k \right),{{R}_{i}}\left( k \right) \right],$ | (2) |
| ${{S}_{i1}}\left( k \right)=\min ({{v}_{i1}}{{\rho }_{i1}}\left( k \right)\Delta t,{{Q}_{i1}}),$ | (3) |
| ${{R}_{i}}\left( k \right)=\min ({{Q}_{i}},{{w}_{i}}{{\rho }_{i,J}}{{\rho }_{i}}\left( k \right)\Delta t).$ | (4) |
式中:qi(k)为(k,k+1)时段元胞i的流入率;Si-1(k)为k时段元胞i-1在自由流状态下能提供的最大车流量(发送函数);Ri(k)为k时段元胞i在拥挤流状态下能接收的最大车流量(接受函数); vi-1为元胞i-1的自由流速度;ρi-1(k)为k时段元胞i-1的车流密度;Qi-1为流入元胞i-1的最大车辆数;wi为激波速度;ρi,J为元胞i的阻塞密度.
1.2 MCTM节点模型依据节点处元胞间的不同连接形式,MCTM节点模型分成3种类型:普通节点模型,合流节点模型,分流节点模型.
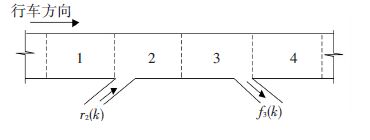
1) 普通节点模型. 若两相邻元胞的连接方式如图 1中元胞2、3所示的简单连接,其模型表达式则与MCTM中的路段模型相类似,见式(2)~(4).
|
图 1 节点模型示意 Figure 1 The schematic diagram of the node model |
2) 合流节点模型. 若两元胞的连接方式如图 1中元胞1、2所示,即为合流连接. 根据下游元胞能否接收来自上游元胞及入口匝道的车流量可划分为
| ${{S}_{i}}k+{{r}_{m,i+1}}\left( k \right)\le {{R}_{i+1}}\left( k \right),\left( 条件\text{ }1 \right)$ |
| ${{S}_{i}}k+{{r}_{m,i+1}}k>~{{R}_{i+1}}k.\left( 条件\text{ }2 \right)$ |
| ${{y}_{i+1}}\left( k \right)=\left\{ _{\min \left( {{S}_{i}}\left( k \right){{R}_{i+1}}\left( k \right) \right)\left( 条件\text{ }2 \right).\text{ }}^{{{S}_{i}}k,\left( 条件\text{ }1 \right)} \right.$ | (5) |
式中:rm,i+1(k)为入口匝道i+1的实测流量. 但若yi+1(k)=Ri+1(k),且rm,i+1(k)>Ri+1(k)时,则令进入下游元胞的流量由入口匝道来提供. 由入口匝道驶入元胞i+1的实际流量ri+1(k)可表示为
| ${{r}_{i+1}}\left( k \right)=\left\{ _{{{R}_{i+1}}\left( k \right){{y}_{i+1}}\left( k \right).\text{ }\left( 条件2 \right)}^{{{r}_{m,i+1}}\left( k \right),\text{ }\left( 条件\text{ }1 \right)} \right.$ | (6) |
3) 分流节点模型. 若两相邻元胞的连接方式如图 1中元胞3、4所示,即为分流连接,此时模型假定每个出口匝道均有无限容量,则
| ${{y}_{i,\text{out}}}\left( k \right)=\min \left( {{S}_{i}}\left( k \right)\frac{{{R}_{i+1}}\left( k \right)}{1{{\beta }_{i}}\left( k \right)} \right).$ | (7) |
式中:yi,out(k)=yi+1(k)+fi(k);fi(k)为出口匝道i的流量;βi(k)为出口匝道i的分流比; (1-βi(k))yi,out(k)为驶入下游元胞的流量;βi(k)yi,out(k)为驶出出口匝道的流量.
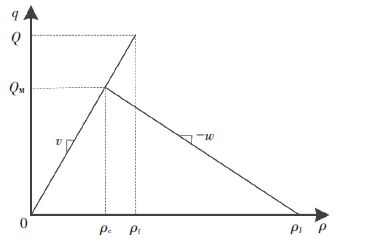
2 MCTM模型的改进 2.1 考虑亚稳态现象的影响亚稳态现象是城市快速路交通流运行中典型的一种实测现象,为降低模型在描述交通流时所产生的误差,尽可能地实现交通流在快速路上的实际运行状态,本文将依据上图所示的基本图,在MCTM模型中模拟亚稳态区域的交通流状态,以提高该模型的真实性及可靠性. 由图 2可得当元胞密度分别为ρc及ρf时,流量与密度的关系为
|
图 2 考虑亚稳态现象的流量-密度基本图 Figure 2 The fundamental diagram between flow and density considering the metastable state |
| $\left\{ \begin{align} & {{Q}_{\text{M}}}=\frac{{{\rho }_{J}}}{{{v}^{1}}+{{w}^{1}}}=v{{\rho }_{c}}, \\ & Q=v{{\rho }_{f}}. \\ \end{align} \right.$ | (8) |
其中ρc为拥挤流向自由流转变的车流密度,ρf为自由流向拥挤流转变的车流密度.
元胞i的交通流状态同样可由元胞密度ρi与临界密度进行对比判断得到:当ρi<ρc时,则元胞i则处于自由流状态;当ρi≥ρf时,则元胞i则处于拥挤流状态;当ρc≤ρi<ρf时,则元胞i则处于亚稳态. 此时,将Zi(k)定义为k时段元胞i的车流状态,当Zi(k)=0时表示车流状态为自由流;当Zi(k)=1时表示车流状态为拥挤流;当Zi(k)=Zi(k-1)时表示车流状态处于亚稳态. 由此即可得状态方程为
| ${{Z}_{i}}\left( k \right)=\left\{ _{{{Z}_{i}}\left( k1 \right), {{\rho }_{c}}<\rho <{{\rho }_{f}}.}^{\begin{smallmatrix} 0 \rho \le {{\rho }_{c}} \\ 1, \rho \ge {{\rho }_{f}}; \end{smallmatrix}} \right.$ | (9) |
引入上述状态方程,则可将k时段元胞i-1的发送函数描述如式(3)所示,而k时段元胞i的接受函数为
| ${{R}_{i}}\left( k \right)=\left( 1{{Z}_{i}}\left( k \right) \right){{Q}_{i}}+{{Z}_{i}}\left( k \right){{w}_{i}}\left( {{\rho }_{J}}{{\rho }_{i}}\left( k \right) \right)\Delta t. $ | (10) |
另外,(k,k+1)时段驶入元胞i的车辆数的一般表达式与MCTM路段模型基本一致.
因此,式(2)、(3)、(9)、(10)即构成了考虑亚稳态的情况下快速路ECTM模型的路段模型.
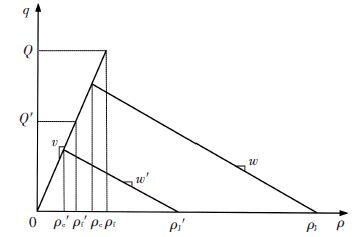
2.2 考虑交通事件的影响当交通事件发生后,受控元胞的通行能力、阻塞密度、临界密度、激波速度将会发生一定程度的折减,如图 3所示,由原本的Q,ρJ,ρc,ρf,w转变为${{Q}^{\prime }},{{\rho }^{\prime }}_{\text{J}},{{\rho }^{\prime }}_{\text{c}},{{\rho }^{\prime }}_{\text{f}},{{w}^{'}}$. 除此之外,由于事件发生路段与正常运行路段的交通流特征有明显差异,因此,为了更加准确地分析交通事件对交通流的影响,应将下游的正常运行路段与上游的事件影响路段分隔开,使得事件发生位置始终处于元胞的边界处. 当交通事件并未发生在节点处时,针对事件发生的不同位置,可分为以下几种情况进行元胞设置的调整.
|
图 3 受交通事件影响的流量密度图 Figure 3 The flow-density diagram under the traffic incident |
1) 当事件发生位置恰好处于初始设置的元胞边界处时,此时初始的元胞设置无需发生改变.
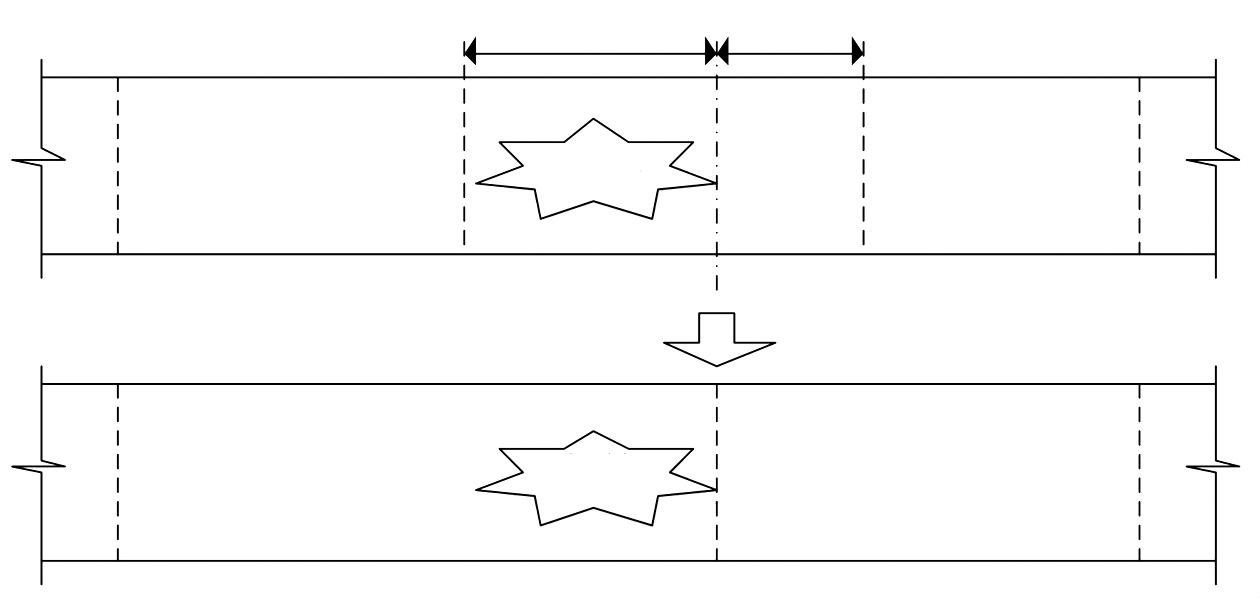
2) 当事件发生位置处于初始设置的元胞i中间,如图 4所示,元胞i上游的事件影响段长度${{l}_{i}}\prime <{{v}_{i}}\Delta t$时,则将这部分路段与上游元胞i-1重组为一个新的元胞i-1;同时,若原元胞i下游的正常运行路段长度$l_{i}^{''}<{{v}_{i}}\Delta t$时,可将这部分路段与原下游元胞i+1重组为一个新的元胞i. 此时,k时段元胞i-1的发送函数Si-1(k)及接受函数Ri-1(k)分别表示为
| ${{S}_{i1}}\left( k \right)=\min \left( {{v}_{i1}}^{\prime }{{\rho }_{i1}}^{\prime }\left( k \right)\Delta t,{{\lambda }_{i1}}{{Q}_{i1}} \right),$ | (11) |
| ${{R}_{i1}}\left( k \right)=\min ({{\lambda }_{i1}}{{Q}_{i1}},{{w}_{i1}}^{\prime }({{\rho }_{J}}^{\prime }{{\rho }_{i1}}^{\prime }\left( k \right)\Delta t).\text{ }$ | (12) |
|
图 4 元胞重组设置Ⅰ Figure 4 The cellular recombinationⅠ |
因为k时段元胞i处于正常运行状态,所以Si(k)及Ri(k)的表示式与式(3)、(4)一致.
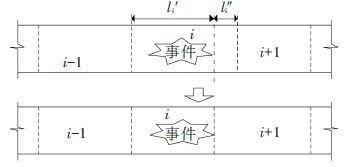
3) 当事件发生于初始设置的元胞i中间,如图 5所示,元胞i上游的事件影响段长度$l_{i}^{'}\ge {{v}_{i}}\Delta t$时,则将这部分路段单独设置为一个新的元胞i;若原元胞i下游的正常运行路段长度$l_{i}^{''}<{{v}_{i}}\Delta t$时,可将这部分路段与下游元胞i+1重组为一个新元胞i+1. 此时,k时段元胞i的发送函数Si(k)及接受函数Ri(k)可分别表示为
| ${{S}_{i}}\left( k \right)=\min \left( {{v}_{i}}^{\prime }{{\rho }_{i}}^{\prime }\left( k \right)\Delta t,{{\lambda }_{i}}{{Q}_{i}} \right)$ | (13) |
| ${{R}_{i}}\left( k \right)=\min ({{\lambda }_{i}}{{Q}_{i}},{{w}_{i}}^{\prime }({{\rho }_{J}}^{\prime }{{\rho }_{i}}^{\prime }\left( k \right)\Delta t).\text{ }$ | (14) |
|
图 5 元胞重组设置Ⅱ Figure 5 The cellular recombination Ⅱ |
k时段元胞i+1的发送函数与接受函数的表示式分别与式(3)、(4)一致.
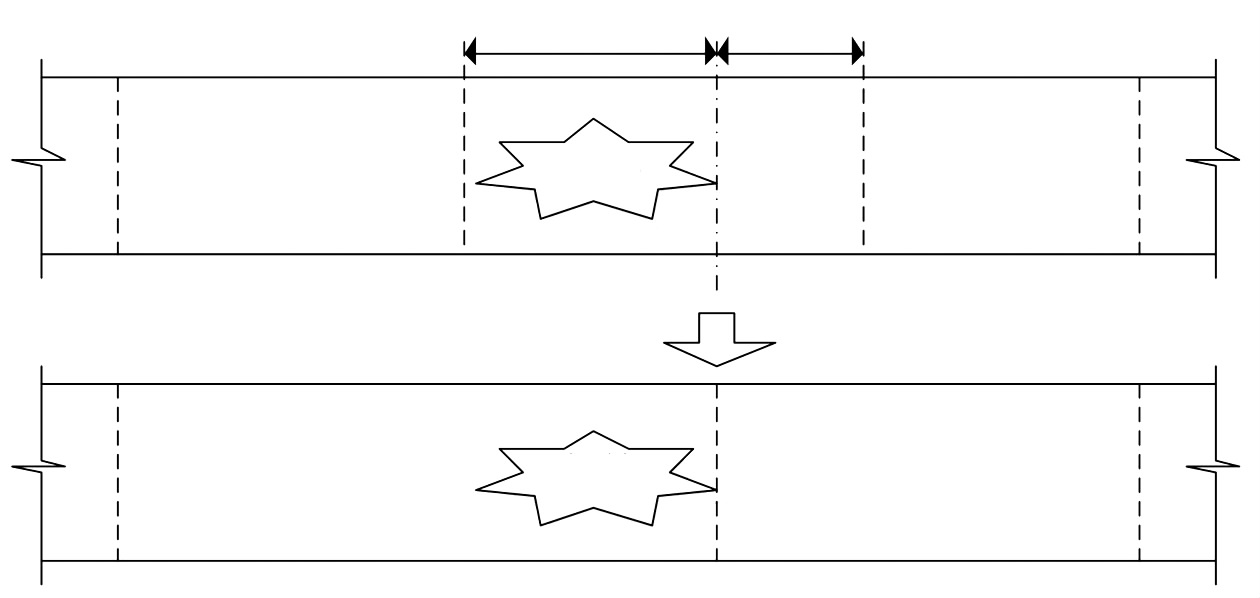
4) 当事件发生于初始设置的元胞i中间,如图 6所示,元胞i上游的事件影响段长度$l_{i}^{'}<{{v}_{i}}\Delta t$时,则将这部分路段与上游元胞i-1重组为一个新的元胞i-1,此时,k时段元胞i-1发送函数Si-1(k)及接受函数Ri-1(k)的表示式与式(11)、(12)相同;若原元胞i下游的正常运行路段长度$l_{i}^{''}{{v}_{i}}\Delta t$时,可将这部分路段单独设置为一个新的元胞i,其发送函数及接受函数的表示式与式(3)、(4)一致.
|
图 6 元胞重组设置Ⅲ Figure 6 The cellular recombination Ⅲ |
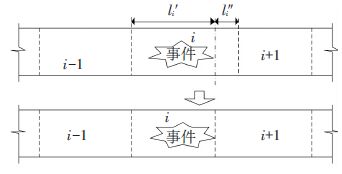
5) 当事件发生于初始设置的元胞i中间,如图 7所示,元胞i上游的事件影响段长度与下游正常运行路段长度均不小于车流自由走行的距离viΔt时,将这两部分路段分别设置为两个新元胞. 其中,新元胞i的发送函数及接受函数的表示式与式(13)、(14)相同,新元胞i+1的表示式则与式(3)、(4)一致.
|
图 7 元胞重组设置Ⅳ Figure 7 The cellular recombination Ⅳ |
为了评价交通拥堵的扩散程度,Wright等[10]提出了拥堵规模这一评价指标,并将其定义为阻塞路段的总量. 然而,这种评价方式仅仅考虑了处于完全阻塞状态的路段,忽略了处于拥堵状态但仍未达到阻塞状态的这部分路段,无法更加充分、有效地反映出拥堵扩散造成的影响. 因此本文为了更清晰、更直接地表征交通事件的影响范围,提出事件影响长度这一评价指标,并将其定义为在交通事件发生后的k时刻,受控区域内所有拥堵元胞的总长度. 其中拥堵元胞是指处于拥挤流状态下的各个元胞. 令I(k)表示交通事件发生后k时刻的影响长度,则依据定义可将其描述为
| $I\left( k \right)=\sum\limits_{j}{{{l}_{j,c}},j\in G.}$ | (15) |
式中lj,c为拥堵元胞j的长度,G为受控区域.
4 实例分析为实现对上文所构建模型的参数标定,本文选取北京西二环一段长为6 508 m,行车方向由南向北的快速路为研究对象. 根据实测数据可知,在2014年5月29日10:25于北京市西二环的复兴门桥附近由南向北方向的内侧车道上发生了一起车辆追尾事故,事件发生位置约在检测器2048上游约300 m处,并占用了一条内侧车道. 该事件造成的事件影响长度为4 548 m,事件清除时间截止于当天11:10时,并于11:45时恢复正常运行状态.
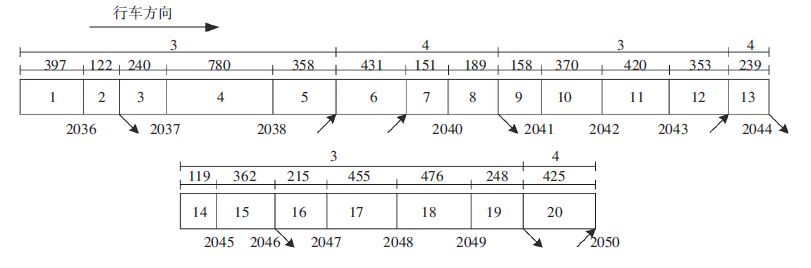
如图 8所示,通过将微波检测器及上下匝道所处位置分别设置为各个元胞的边界,将所选路段划分为20个元胞,元胞内的数字即为元胞编号,最顶层的数字代表的是元胞内路段的车道数,元胞上底层的数字代表的是各个元胞的长度,单位为米,下面的数字表示的是各个微波检测器的位置编号,各个箭头所处位置即为匝道所在位置.
|
图 8 元胞划分示意 Figure 8 The schematic diagram of the cell division |
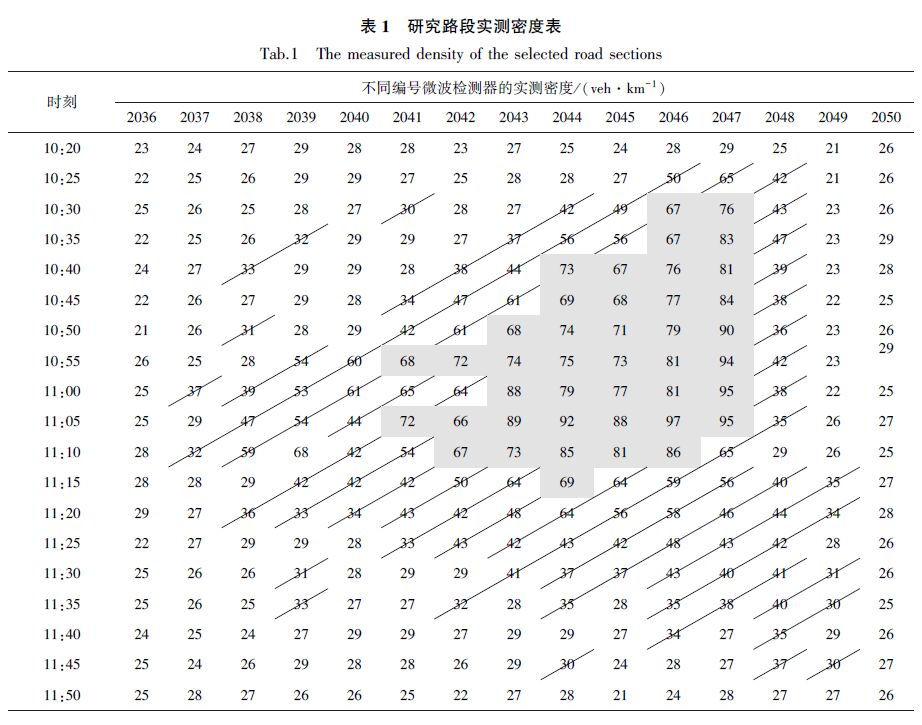
表 1为事件发生所处时段为10:20—11:45时的实测密度. 表中最左侧为交通事件影响时段内时间间隔为5 min的时点,最上方为研究路段内各个微波检测器的位置编号,中间标识的是在不同时点各个检测器单车道的实测密度值(veh/km). 其中,密度值处于(0,30)的路段为正常运行状态,标记为白色;密度值处于[30,66)的路段处于拥挤状态,标记为斜纹;密度值≥66的路段处于严重拥挤状态,标记为灰色底纹.
| 表 1 研究路段实测密度表 Table 1 The measured density of the selected road sections |
根据微波车辆检测器以及人工调查所获取的数据,结合文献[6]的参数标定方法,对自由流速度、非瓶颈路段通行能力、瓶颈路段通行能力、激波速度、阻塞密度5个参数分别进行标定,其中自由流速度为70~80 km/h,单车道路段通行能力为1 700~2 200 veh/h,激波速度wi为21~26 km/h,单车道阻塞密度ρJ,i为84~95 veh/km,事发路段所属元胞的通行能力的折减系数为49%.
根据事件数据可知,事件发生位置处于第17个元胞的中间位置,从而可将此元胞划分为两部分,其中上游的事件影响段长度$l_{17}^{'}$为155 m,下游的路段长度$l_{17}^{''}$为300 m. 而由于单位时间内车辆自由走行的距离vΔt为114 m,明显满足$l_{17}^{'}\ge v\Delta t$,及$l_{17}^{''}\ge v\Delta t$的条件,因此可将这两部分路段分别单独设置为一个新的元胞.
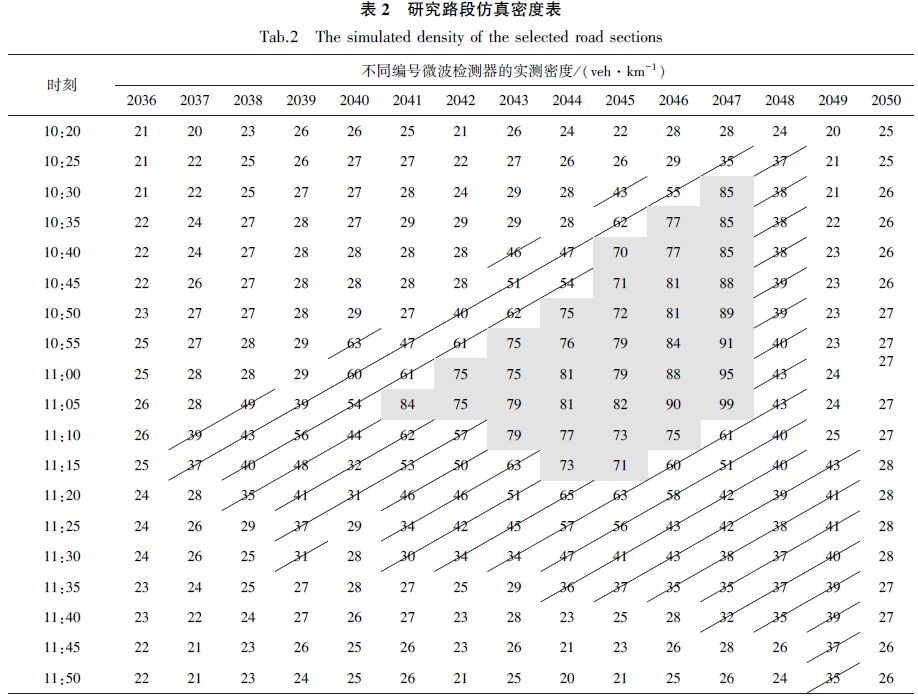
此时,对此事件进行仿真,为了降低仿真的随机误差,本文选择10次仿真的平均值作为仿真的最终结果,并最终得出仿真密度值如表 2所示,将其与实测密度等势图进行对比可以发现,两者的变化趋势近乎一致. 另外,通过计算得出主要的交通事件影响范围评价指标,并将其与实测数据进行对比,误差均在可接受范围内. 事件实际持续时间为80 min,而事件仿真持续时间则为85 min,误差为6.25%;事件实际影响长度为4 548 m,而事件仿真影响长度则为4 670 m,误差为2.68%. 另外,经分析,若在满足划分条件的前提下,将长度较大的元胞进一步划分为等长的元胞进行仿真分析,其结果与之前的计算结果比较而言并无显著差异,但是计算效率却大大降低. 相反,若将相邻的几何特征类似的元胞进一步合并,其计算效率虽有了显著的提高,但是计算误差也明显增加,计算精度较低.
| 表 2 研究路段仿真密度表 Table 2 The simulated density of the selected road sections |
综上所述,基于MCTM的快速路交通事件影响范围预测模型不仅能清晰地反映出路段在发生交通事件后的拥堵传播状态,并且能够获取较为精确的影响范围评价指标值,从而验证了该模型的合理性.
5 结 论1) 在MCTM模型的基础上,结合考虑快速路的交通特性及交通事件的影响,构建了快速路交通事件影响范围预测模型,并对其进行了验证分析.
2) 基于MCTM模型,通过在路段模型中考虑亚稳态对交通流的影响,真实刻画了交通流运行中的典型现象. 并以实际采集的交通事件下的检测器数据为依据,对事发路段的主要交通流参数进行修正. 以交通流密度作为状态变量,针对交通事件发生的不同位置,调整元胞的划分方式,将特征差异较大的事发路段与正常运行路段进行区别分析,重新确定了事件影响下各个元胞的发送函数及接受函数.
3) 提出事件影响长度这一评价指标,结合实测数据,根据所得模型对所选快速路特征路段的交通流运行状态进行模拟,得到车辆出行的详细信息,更清晰直接地表征交通事件的影响范围,进而对交通事件影响范围的评价指标进行估算,所得结果与实测数据相近,从而验证了该模型的有效性.
| [1] |
SCHNHOF M, HELBING D. Empirical features of congested traffic sates and their implications for traffic modeling[J].
Transportation Science,2007, 41 (2) : 135-166.
DOI: 10.1287/trsc.1070.0192 ( 0) 0)
|
| [2] |
TANG T Q, HUANG H J, WONG S C, et al. A new car-following model with consideration of the traffic interruption probability[J].
Chinese Physics B,2009, 18 : 975-983.
DOI: 10.1088/1674-1056/18/3/022 ( 0) 0)
|
| [3] |
BAYKAL-GVRSOY M. Modeling traffic flow interrupted by incidents[J].
European Journal of Operational Research,2009, 195 (1) : 127-138.
DOI: 10.1016/j.ejor.2008.01.024 ( 0) 0)
|
| [4] |
SKABARDONIS A, VARAIYA P, PETTY K F. Measuring recurrent and nonrecurrent traffic congestion[C]//Proceedings of 82nd Transportation Research Board Annual Meeting. Washington DC: Journal of the Transportation Research Board, 2003: 118-124.
( 0) 0)
|
| [5] |
KWON J, VARAIYA P. The congestion pie: delay from collisions, potential ramp metering gain, and excess demand[C]// Proceedings of 84th Transportation Research Board Annual Meeting. Washington DC: Journal of the Transportation Research Board, 2005:1-21.
( 0) 0)
|
| [6] |
MUÑOZ L, SUN X, HOROWITZ R, et al. Traffic density estimation with the cell transmission model[C]//Proceedings of the American Control Conference. Denver: IEEE, 2003: 3750-3755.
( 0) 0)
|
| [7] |
MUÑOZ L, SUN X, SUN D, et al. Methodological calibration of the cell transmission model[C]// Proceedings of American Control Conference. Boston: IEEE, 2004: 798-803.
( 0) 0)
|
| [8] |
DAGANZO C F. The cell transmission model,part II: network traffic[J].
Transportation Research Part B,Methodological,1995, 29 (2) : 79-93.
DOI: 10.1016/0191-2615(94)00022-R ( 0) 0)
|
| [9] |
DAGANZO C F. The cell transmission model: a dynamic representation of highway traffic consistent with the hydrodynamic theory[J].
Transportation Research Part B,Methodological,1994, 28 (4) : 269-287.
DOI: 10.1016/0191-2615(94)90002-7 ( 0) 0)
|
| [10] |
WRIGHT C, ROBERG P. The conceptual structure of traffic jams[J].
Transport Policy,1998, 5 (1) : 23-35.
DOI: 10.1016/S0967-070X(98)00006-7 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48