高精度的车辆位置信息对车辆行为安全分析具有重要意义. 近年来,基于机器视觉的车辆定位逐渐成为自主导航的研究热点[1]. 相较于传统的定位方法(GPS、INS、里程计等),视觉里程计不存在信号盲区、不受车轮打滑影响,具有自主、定位精度高和不容易受干扰等优点[2-3]. 文献[4]提出了一种基于街景图像序列的自主定位方法,预先拍摄全方位街景图像存储在数据库中,在车辆行驶过程中实时利用两个摄像头从不同角度拍摄街景,然后将拍摄的街景与预存的全方位街景进行匹配,利用三角测量的方法定位车辆的精确位置. 这种方法的特点是定位精度较高,但是需要预先建立数据库,即全方位拍摄街景,因此费时费力,不适用于未经采集全景的车辆实时定位方法. 文献[5]提出基于路标的车辆定位方法,根据检测到的路面标志与车辆的相对距离以及数据库中的路标实际坐标精确估计车辆位置,其预存过程同样耗费时间. 文献[6]提出的基于Hu矩和灰度特征融合的车辆轨迹提取方法,根据局部特征匹配所得特征点计算单应性矩阵,进而根据图像偏移量估计车辆运动轨迹实现自主定位. 该方法定位准确,但运行效率较低,而且受累计误差影响轨迹随时间产生漂移. 文献[7]采用视觉特征完成车辆定位和自主运动评估的方法速度也相对缓慢. 基于图像特征点匹配的车辆定位方法精确性好,但是时间效率太低. 经过近30年的发展,光流法对于图像运动的估计可以满足一定的精度和稳定度的要求,并且由于计算速度快,基于光流法的视觉里程计已经可以达到实际应用的要求[8]. 文献[9]提出的基于光流法的机器人视觉导航方法可类比应用于车辆,研究了全景相机、鱼眼镜头以及球面全景立体成像系统所获取图像的光流效果,可以实现避障以及障碍物深度估计. 文献[10]提出基于后泊车摄像头的精确视觉测程方法,通过ESM算法(efficient second order minimisation)对齐图像计算相对偏移量,融合GPS实现精确定位. 文献[11-12]提出的基于光流法的单目视觉里程计研究,通过卡尔曼滤波将光流法和特征点匹配算法进行融合,考虑实时性的基础上降低误差实现平坦路面上的自主定位. 文献[13]研究的昆虫视觉启示的光流复合导航方法同样采用了卡尔曼滤波器修正累积误差. 为了保证实时性且提高定位精度,本文融合改进Lucas-Kanade和FAST(features from accelerated segment test,基于加速分割测试的特征)特征点获得车辆的相对偏移量,然后对结果进行误差估计,弥补定位精度.
1 基于路面光流的车辆运动估计优化方法为了加快光流计算速度,本文仅对图像的FAST特征点进行光流计算跟踪,同时也提高了光流计算的精度和稳定性;然后根据路面图像间偏移量与旋转角度估计车辆运动信息;最后通过误差估计优化更新车辆位置,实现精确定位.
1.1 基于改进Lucas-Kanade计算FAST特征点的光流文献[14]提出一种基于金字塔分层和仿射变换的改进Lucas-Kanade算法,其相较于Lucas-Kanade算法直接对原始图像通过最小二乘法来求解像素点在周围邻域内的光流方程从而获得光流,具有计算速度快、稳定性和精确性高的优势. 本文将其引入到车辆定位实现中,增强该优化方法的实时性.
光流法的原理是寻找到像素点的适合运动向量和变换矩阵使得图像间灰度差最小. 假设前一帧图像I的一个像素点u=[ux,uy]Τ,后一帧图像J一个像素点v=[ux+dx,uy+dy]Τ与之相匹配,即灰度差最小,则d=[dx,dy]Τ为图像I在点u处的光流.
定义两帧图像间的变换矩阵$A=\left[ _{{{d}_{yx}} 1+{{d}_{yy}}}^{1+{{d}_{xx}} {{d}_{xy}}} \right]$,其中dxx,dxy,dyx,dyy为仿射变形参数,仿射变换是两个向量空间之间的一种变换关系,是对坐标进行放缩、旋转、平移等后取得新坐标的过程. 则灰度差表示为
| $\begin{align} & \varepsilon \left( d,A \right)=({{d}_{x}},{{d}_{y}},{{d}_{xx}},{{d}_{xy}},{{d}_{yx}},{{d}_{yy}})= \\ & \sum\limits_{x={{w}_{x}}}^{{{w}_{x}}}{\sum\limits_{y={{w}_{y}}}^{{{w}_{y}}}{{{\left( I\left( x+u \right)J\left( Ax+d+u \right) \right)}^{2}}}}. \\ \end{align}$ | (1) |
其中:wx、wy设定图像上矩形窗口的大小为(2wx+1)×(2wy+1),一般取值为7、8、10、20.
本文采用的改进Lucas-Kanade算法首先对前后两帧图像分别通过采样构建金字塔,从最顶层开始跟踪前一帧图像中每个FAST特征点(标准FAST-9检测器[15]),计算光流d和变换矩阵A,不断迭代使得通过d和A变换后的前后两帧间FAST特征点在这层的灰度差异ε最小;然后再把这一层的结果传递给下一层,重新计算光流和仿射变换矩阵,再传递给下一层,直至传递到最后一层(即原始图像层),这一层计算出来的光流和变换矩阵作为最后的FAST特征点光流和变换矩阵的结果.
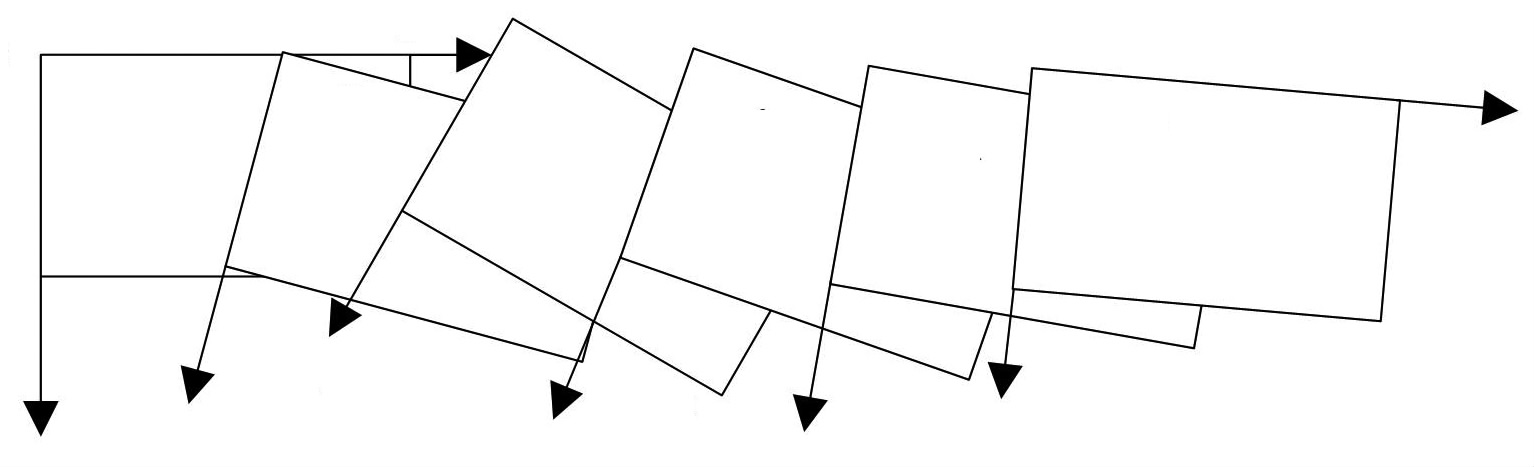
1.2 车辆运动估计本文的车载单目相机垂直地面采集图像,因此图像间只存在旋转和平移变换. 在得到多组FAST特征点光流后,根据单应性矩阵H可计算出第i与i+1帧图像间的变化量Ti=[xi,yi,θi]Τ,本文以第1帧图像的坐标系为基准(初始坐标系),如图 1所示,对得到的图像间变量Ti进行坐标系转换,最终获得初始坐标系下x、y轴方向的偏移量Xi与Yi,即
| $\left\{ \begin{align} & {{X}_{i}}={{x}_{i}}\cos \sum\limits_{k=1}^{i}{{{\theta }_{k}}}{{y}_{i}}\sin \sum\limits_{k=1}^{i}{{{\theta }_{k}}}, \\ & {{Y}_{i}}={{x}_{i}}\sin \sum\limits_{k=1}^{i}{{{\theta }_{k}}+{{y}_{i}}}\cos \sum\limits_{k=1}^{i}{{{\theta }_{k}}}. \\ \end{align} \right.$ | (2) |
|
图 1 帧间坐标系转化 Figure 1 Coordinates transformation between image frames |
由于相机与车体运动是刚体运动,按照图像像素与实际坐标单位米的转化比例即可获得车辆位置信息.
1.3 车辆偏移误差估计由式(2)易知,车辆定位所用旋转角度是一个累计值,且每组Ti=[xi,yi,θi]Τ是测量值,因此,随着时间推移误差积累越来越大,车辆轨迹会发生漂移. 本文通过自定义误差估计方法(error estimation,EE)优化更新车辆相对偏移量,弥补轨迹偏差,具体算法如下.
设上述计算所得测量值Ti=[xi,yi,θi]Τ的每个分量是由真实值$({{{\bar{x}}}_{i}},{{{\bar{y}}}_{i}},{{{\bar{\theta }}}_{i}})$与误差$({{{\tilde{x}}}_{i}},{{{\tilde{y}}}_{i}},\tilde{\theta })$相加而得,即定义${{x}_{i}}={{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}}{{y}_{i}}={{{\bar{y}}}_{i}}+{{{\tilde{y}}}_{i}}{{\theta }_{i}}={{{\bar{\theta }}}_{i}}+{{{\tilde{\theta }}}_{i}}$,则第i与i+1帧图像在初始坐标系下的x、y方向偏移量Xi与Yi变化分别为
| $\left\{ \begin{align} & {{x}_{i}}={{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}}{{y}_{i}}={{{\bar{y}}}_{i}}+{{{\tilde{y}}}_{i}}{{\theta }_{i}}={{{\bar{\theta }}}_{i}}+{{{\tilde{\theta }}}_{i}} \\ & {{X}_{i}}=x\cos \sum\limits_{k=1}^{i}{{{\theta }_{k}}{{y}_{i}}\sin }\sum\limits_{k=1}^{i}{{{\theta }_{k}}=({{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}})\cos }\sum\limits_{k=1}^{i}{({{{\bar{\theta }}}_{k}}+} \\ & {{{\tilde{\theta }}}_{k}})\left( {{{\bar{y}}}_{i}}+{{{\tilde{y}}}_{i}} \right)\sin \sum\limits_{k=1}^{i}{\left( {{{\bar{\theta }}}_{k}}+{{{\tilde{\theta }}}_{k}} \right)=\left( {{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}} \right)}. \\ & \left( \cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}}}}} \right)(\bar{y}+ \\ & {{{\tilde{y}}}_{i}})\left( \sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}+\cos }}\sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\sin }\sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}} \right), \\ & {{Y}_{i}}={{x}_{i}}\sin \sum\limits_{k=1}^{i}{{{\theta }_{k}}+{{y}_{i}}\cos }\sum\limits_{k=1}^{i}{{{\theta }_{k}}=({{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}})}\cdot \\ & \left( \sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\cos }\sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}+\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}}}} \right)+({{{\bar{y}}}_{i}}+ \\ & {{{\tilde{y}}}_{i}})\left( \cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{k}}\sin }}}\sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{k}}} \right). \\ \end{align} \right.$ | (3) |
由于x方向的偏移量${{x}_{i}}={{{\bar{x}}}_{i}}+{{{\tilde{x}}}_{i}}$,其真值${{{\bar{X}}}_{i}}=\bar{x}\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}{{{\bar{y}}}_{i}}\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}$,则代入式(3)计算其误差${{{\tilde{x}}}_{i}}$为
| $\begin{align} & {{{\tilde{X}}}_{i}}=\bar{x}(\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}(\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}}-1)- \\ & \sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}})+{{{\tilde{x}}}_{i}}(\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}- \\ & \sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}-{{{\bar{y}}}_{i}}(\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}(\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}-1)+ \\ & \cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}})-{{{\tilde{y}}}_{i}}(\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}+ \\ & \cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}). \\ \end{align}$ | (4) |
同理,计算y方向偏移量Yi的误差${\tilde{Y}}$. 假设在x和y方向的偏移量误差及两帧图像间的旋转角度误差都服从正态分布,即${{{\tilde{x}}}_{i}}\tilde{\ }N(0,{{\delta }^{2}}_{x}){{{\tilde{y}}}_{i}}\tilde{\ }N(0,{{\delta }^{2}}_{y}){{{\tilde{\theta }}}_{i}}\tilde{\ }N(0,{{\delta }^{2}}_{\theta })$,则分别有
| $\left\{ \begin{align} & \sum\limits_{k=1}^{i}{{{{\tilde{x}}}_{i}}}\tilde{\ }N\left( 0,i{{\delta }^{2}}_{x} \right) \\ & \sum\limits_{k=1}^{i}{{{{\tilde{y}}}_{i}}}\tilde{\ }N(0,i{{\delta }^{2}}_{y}) \\ & \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}}\tilde{\ }N(0,i{{\delta }^{2}}_{\theta }) \\ \end{align} \right.$ | (5) |
| $\left\{ \begin{align} & E(\cos \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}})={{e}^{\frac{-i{{\delta }^{2}}_{\theta }}{2}}}, \\ & E(\sin \sum\limits_{k=1}^{i}{{{{\tilde{\theta }}}_{i}}})=0. \\ \end{align} \right.$ | (6) |
将式(5)、(6)代入式(4)中求得初始坐标系下x方向偏移量Xi的误差期望为
| $\begin{align} & E[{{{\tilde{X}}}_{i}}|{{{\bar{x}}}_{i}},{{{\bar{y}}}_{i}},{{{\bar{\theta }}}_{i}}]={{{\bar{x}}}_{i}}\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}({{e}^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}1) \\ & {{{\bar{y}}}_{i}}\left( \sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}\left( {{e}^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}1 \right) \right) \\ \end{align}$ | (7) |
由于式(7)所需要的偏移量及旋转角度真实值在实际中是不可测的,为使结果可用,平均值期望为
| $\begin{align} & E[E({{{\tilde{X}}}_{i}})|{{x}_{i}},{{y}_{i}},{{\theta }_{i}}]= \\ & E\{{{{\bar{x}}}_{i}}(\cos \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}({{e}^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}1))- \\ & {{{\bar{y}}}_{i}}\sin \sum\limits_{k=1}^{i}{{{{\bar{\theta }}}_{i}}}({{e}^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}1)\}= \\ & E\{\left( {{x}_{i}}{{{\tilde{x}}}_{i}} \right)(\cos \sum\limits_{k=1}^{i}{\left( {{\theta }_{i}}{{{\tilde{\theta }}}_{i}} \right)}({{e}^{^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}}1) \\ & \left( {{y}_{i}}{{{\tilde{y}}}_{i}} \right)(\sin \sum\limits_{k=1}^{i}{\left( {{\theta }_{i}}{{{\tilde{\theta }}}_{i}} \right)}({{e}^{^{\frac{i{{\delta }^{2}}_{\theta }}{2}}}}1)\}= \\ & \left( {{e}^{i{{\delta }^{2}}_{\theta }}}{{e}^{\frac{i{{\delta }^{2}}_{\theta }}{2}}} \right)\left( {{x}_{i}}\cos \sum\limits_{k=1}^{i}{{{\theta }_{i}}}-{{y}_{i}}\sin ~\sum\limits_{k=1}^{i}{{{\theta }_{i}}} \right). \\ \end{align}$ | (8) |
同上述过程,初始坐标系下y方向偏移量Yi的误差平均值期望为
| $\begin{align} & E\left[ E\left( {{{\tilde{Y}}}_{i}} \right)|{{x}_{i}},{{y}_{i}},{{\theta }_{i}} \right]=\left( {{e}^{i{{\delta }^{2}}_{\theta }}}{{e}^{i{{\delta }^{2}}_{\theta }2}} \right)\cdot \\ & {{x}_{i}}\sin ~\sum\limits_{k=1}^{i}{{{\theta }_{i}}}+{{y}_{i}}\cos ~\sum\limits_{k=1}^{i}{{{\theta }_{i}}}. \\ \end{align}$ | (9) |
因此,以初始坐标系为基准,对第i与i+1帧图像间偏移量进行误差估计,优化更新后的结果ΔT=[ΔxiΔyi]T计算如下
| $\left[ \begin{array}{l} \Delta {x_i}\\ \Delta {y_i} \end{array} \right] = \left[ \begin{array}{l} {X_i} - E[E({{\tilde X}_i})|{x_i},{y_i},{\theta _i}]\\ {Y_i} - E[E({{\tilde Y}_i})|{x_i},{y_i},{\theta _i}] \end{array} \right].$ | (10) |
最后将修正后的相对偏移量累积叠加并映射到世界坐标系中即可完成车辆精确定位.
2 实验结果分析本文通过长安大学智能车进行试验. 采用德国basler aca1600-60 gm-gc型号的工业相机采集图像,图像分辨率为1 600×1 200,采集频率是60 Hz,车辆平均速度为9 km/h,图像序列对应真实环境的路面实况. 以一段直行路段中第690~700帧图像作为测试样本,基于改进Lucas-Kanade计算FAST特征点处光流,结果如图 2所示.

|
图 2 第690~695帧图像中FAST特征点的光流 Figure 2 Optical flow of FAST feature points from the 690th to 695th frame |
图 2是对第690~695帧整幅图像进行特征点光流计算的结果,特征点的光流反映了图像间的偏移量,进而体现了车辆的运动趋势. 实际情况下为加快算法运行效率,可以只选取图像感兴趣区域(如:缩小检测特征点的图像区域)进行特征点及光流检测,其在算法精度上并没有影响. 然后根据图像特征点光流的跟踪结果,采用上述式(2)计算第690~700帧图像间偏移量Xi和Yi(i=690,691,…, 700);通过本文自定义的误差估计方法对偏移量进行误差估计,优化修正偏移量得到最终结果Δxi和Δyi.由于车载单目相机垂直地面采集图像,相机与车体运动是刚体运动,因此,图像坐标系下的图像帧间偏移量Δxi和Δyi只需要根据图像像素与实际坐标单位米的转化比例即可获得世界坐标系下的车辆相对运动偏移量,最后绘制运行轨迹完成车辆精确定位,图像帧间偏移量见表 1.
| 表 1 图像帧间偏移量 Table 1 The offset between image frames |
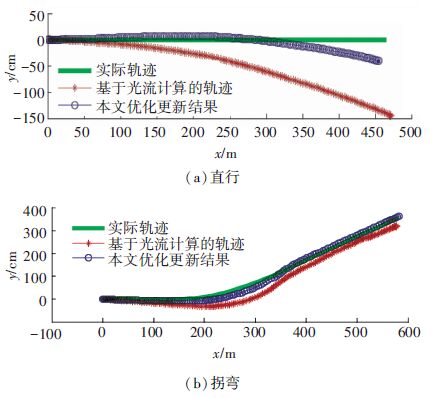
本文运动估计优化方法测试了多段不同的车辆运行轨迹,其中两组结果如图 3所示. 显而易见,随时间推移累积误差越来越大,计算结果逐渐偏离原始轨迹,直行时的偏差小于拐弯时的. 然而采用本文的优化方法对误差进行估计后,漂移误差得以适当修正,轨迹更接近实际结果,确保了一定范围内精确的车辆位置信息.
|
图 3 两组车辆轨迹对比 Figure 3 Contrast results of two vehicle trajectories |
本文基于光流的优化方法与传统基于特征点匹配(SIFT、SURF)的定位方法在处理时间上相比也有优势,其时间消耗都主要在于获得图像间相对偏移量,分别完成该步的运行时间见表 2. 从表中可看出采用SIFT算法的处理平均时间是0.858 2 s,采用SURF算法的处理平均时间是0.658 7 s,而本文优化方法处理平均时间是0.208 1 s,更好地满足车辆自主定位的实时性要求.
| 表 2 运行时间对比 Table 2 Contrast of running time |
1) 提出了一种结合光流法的车辆运动估计优化方法. 采用改进的Lucas-Kanade算法跟踪FAST特征点计算图像间偏移量,通过自定义的误差估计算法优化更新结果,将其映射到世界坐标系中获得车辆运行轨迹,总体上保证了车辆定位的实时性及精确性.
2) 使用单目摄像机,降低了对硬件设备的要求;基于改进Lucas-Kanade算法计算FAST特征点的光流,突出了光流法的实时性并且克服了其精度差的缺点;车辆偏移量误差估计在一定时间内解决了累积误差所引起的轨迹漂移问题.
3) 经过测试多组不同车辆行驶轨迹,证明该优化方法兼顾车辆自主定位的实时性和精度,具有较好的定位效果. 相较于基于特征点匹配的车辆定位计算时间短,与常用的光流法比较,轨迹更加精确、光滑.
| [1] |
LOVEGROVE S J. Parametric dense visual SLAM [D]. London: Imperial College London, 2011.
( 0) 0)
|
| [2] |
SHI H, YAN L, LIU B, et al. GPS/SINS integrated navigation algorithm aided by scene matching[J].
Journal of Tsinghua University (Science and Technology),2008, 48 (7) : 1182-1185.
( 0) 0)
|
| [3] |
SONG Xiaojing, SONG Zibin, et al. Optical flow-based slip and velocity estimation technique for unmanned skid-steered vehicles [C]//Intelligent Robots and Systems, 2008 IEEE/RSJ International Conference on. Nice: IEEE, 2008: 101-106.
( 0) 0)
|
| [4] |
UCHIYAMA H, DEGUCHI D, TAKAHASHI T, et al. Ego-localization using streetscape image sequences from in-vehicle cameras [C]//Intelligent Vehicles Symposium, 2009 IEEE International Conference on. Shaanxi: IEEE, 2009: 185-190.
( 0) 0)
|
| [5] |
WU Tao, RANGANATHAN A.Vehicle localization using road markings [C] // Intelligent Vehicles Symposium, 2013 IEEE International Conference on. Gold Coast City: IEEE, 2013: 1185-1190.
( 0) 0)
|
| [6] |
ZHOU Jingmei, ZHAO Xiangmo, XU Zhigang, et al. Algorithm of vehicle trajectory extraction using fusion of Hu moments and grayscale feature[J].
Information Technology Journal,2014, 13 (11) : 1770-1778.
DOI: 10.3923/itj.2014.1770.1778 ( 0) 0)
|
| [7] |
PINK O, MOOSMANN F, BACHMANN A. Visual features for vehicle localization and ego-motion estimation [C] // Intelligent Vehicles Symposium, 2009 IEEE International Conference on. Shaanxi: IEEE, 2009: 254-260.
( 0) 0)
|
| [8] |
SUN D, ROTH S, BLACK M J. Secrets of optical flow estimation and their principles [C] // Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. San Francisco: IEEE, 2010: 2432-2439.
( 0) 0)
|
| [9] |
班跃海. 基于光流法的机器人视觉导航 [D]. 南京: 南京理工大学, 2012.
BAN Yuehai. Vision-based mobile robot navigation based on optical flow [D]. Nanjing: Nanjing University of Science and Technology. 2012. (  0) 0)
|
| [10] |
LOVEGROVE S J, DAVISON A J, et al. Accurate visual odometry from a rear parking camera [C]. Intelligent Vehicles Symposium, IEEE, 2011: 788-793.
( 0) 0)
|
| [11] |
郑驰, 项志宇, 刘济林. 融合光流与特征点匹配的单目视觉里程计[J].
浙江大学学报(工学版),2014, 48 (2) : 279-284.
ZHENG Chi, XIANG Zhiyu, LIU Jilin. A monocular visual odometry based on the fusion of optical flow and feature points matching[J]. Journal of Zhejiang University(Engineering Science),2014, 48 (2) : 279-284. (  0) 0)
|
| [12] |
郑驰. 基于光流法的单目视觉里程计研究 [D]. 杭州: 浙江大学, 2013.
ZHENG Chi. Monocular visual odometry based on optical flow methods [D]. Hangzhou: Zhejiang University, 2013. (  0) 0)
|
| [13] |
潘超. 昆虫视觉启发的光流复合导航方法研究[D]. 武汉: 华中科技大学, 2011.
PAN Chao.An optical flow-based complex navigation method inspired by insect vision [D]. Wuhan: Huazhong University of Science and Technology, 2011. (  0) 0)
|
| [14] |
BOUGUET J. Pyramidal implementation of the Lucas Kanade feature tracker description of the algorithm[J].
Intel Corporation Microprocessor Research Labs Tech Rep,2000, 22 (2) : 363-381.
( 0) 0)
|
| [15] |
王蒙, 戴亚平. 基于FAST角点检测的局部鲁棒特征[J].
北京理工大学学报,2013, 33 (10) : 1045-1050.
WANG Meng, DAI Yaping. Local Robust Feature Based on FAST Corner Detection[J]. Transaction of Beijing Institute of Technology,2013, 33 (10) : 1045-1050. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


