栓钉抗剪连接件是目前在钢-混凝土组合桥梁中应用最为广泛的抗剪连接件. 在实际受力过程中,栓钉抗剪连接件是保证钢梁与混凝土桥面板共同工作,并发挥“1+1>2”组合作用的关键[1],结合面上的所有剪力完全由其承担. 在车辆等反复荷载作用下,栓钉连接件会处于较高的疲劳应力状态,因此也是组合梁中最为薄弱的环节. 现阶段,中国早期修建的一批组合桥梁已进入了生命周期的一个阶段点,结构和组成构件的力学性能开始出现退化现象[2],尤其是抗剪连接件在疲劳荷载作用下的安全性和耐久性问题非常值得关注. 迄今为止,各国学者已经对栓钉连接件作了较为深入、全面的研究,研究内容包括栓钉连接件的抗剪承载力[3],结合面上的相对滑移[4]以及连接件的抗疲劳性能[5]. 然而,对栓钉连接件在承受一定循环次数疲劳荷载后的剩余承载力的研究相对较少,至今仍然没有一个适用的理论模型来描述栓钉连接件在疲劳荷载作用下的静力承载力退化问题.
根据疲劳累积损伤理论,钢-混凝土组合梁在反复荷载作用下,每一次的加载都会对栓钉连接件造成一定程度的疲劳损伤. 随着加载次数的增加,栓钉和混凝土之间的相互作用会发生改变,栓钉周围混凝土逐渐被压碎,栓钉本身的疲劳裂纹也会不断扩展,造成栓钉连接件不断地发生疲劳累积损伤,进而导致栓钉连接件抗剪承载力退化. 早在上个世纪60年代,已有研究者在进行栓钉推出试件的疲劳试验时,发现了栓钉连接件抗剪承载力的退化现象. 1967年,Mainstone[6]在试验中发现两个推出试件承受疲劳荷载后的承载能力发生了退化,只有不到初始静力强度的50%. 1976年,Roderick等[7]在组合梁的试验中,发现其中一片试验梁在承受疲劳荷载后出现了明显的过早破坏. 1985年,Oehlers等[8-9]分别对5个经历过疲劳加载的推出试件进行了单调静载试验,发现推出试件的极限承载力只有预期强度的51%~73%. 2005年,薛伟辰等[10]对栓钉连接件在周期荷载下的抗剪性能研究时发现,在反复荷载下,C50中13 mm、16 mm和19 mm栓钉的极限承载力比单调荷载时分别平均下降了31.33%、19.83%和13.32%. 可见,大量试验都直接或间接地发现了栓钉连接件的抗剪承载力随疲劳循环次数发生退化的现象. 然而,迄今为止专门针对栓钉疲劳加载后剩余承载力的研究成果仍鲜见报道.
本文以桥梁工程中应用最为广泛的栓钉连接件为研究对象,在栓钉推出试件静载破坏试验、完全疲劳试验以及非完全疲劳破坏试验的基础上,对已有的栓钉连接件非完全疲劳推出试验数据进行归纳和总结. 同时,基于剩余强度理论,提出栓钉剩余承载力的概念,推导出栓钉连接件的剩余承载力计算模型,结合本文和以往的试验数据对该模型进行拟合,确定其参数. 最后,通过若干文献的试验数据再对该模型的正确性进行验证分析.
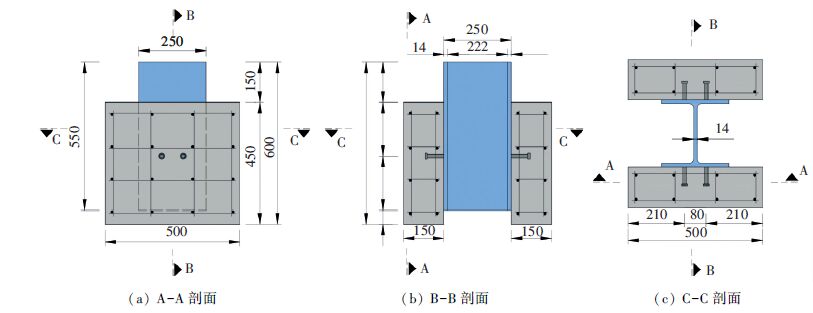
1 试验设计 1.1 试件尺寸推出试验的试件设计参考欧洲规范4中推荐的推出试件尺寸及配筋[11],混凝土选用的等级为C50,普通钢筋采用10 mm的HPB300级热轧钢筋,钢板选用桥梁上常用的Q345钢材. 钢梁采用厚度为14 mm的工字钢,长度为550 mm,两侧各焊两个13×70的栓钉,材料为符合规范要求的ML-15,混凝土翼板由两块450 mm×500 mm×150 mm的混凝土板组成,其内配置两层钢筋网,具体尺寸如图 1所示. 另外,浇筑试件混凝土时,在钢梁与混凝土接触表面刷油以避免钢板与混凝土粘结对试验结果的影响.
|
图 1 推出试件尺寸及构造(mm) Figure 1 he size and structure of the push-out specimen (mm) |
在进行栓钉连接件的推出试验之前,首先对组成推出试件的材料进行相关力学性能试验. 试验测得混凝土的立方体强度为59.7 MPa,弹性模量为3.59×104 MPa,栓钉连接件的弹性模量为2.0×105 MPa,屈服强度为442 MPa,极限强度为525 MPa.
1.2 加载方案本次试验在多功能结构试验系统(JAW-500K)上完成,该系统配有量程为500 kN的低摩擦球铰的电液伺服加载作动器,可用于静力加载和动力加载. 试验加载内容分为3组:1)静载破坏试验,包括3个试件,编号为SCP-1、SCP-2、SCP-3,目的是确定栓钉连接件的静力极限承载力Pu;2)完全疲劳试验,包括3个试件,编号为FCP-1、FCP-2、FCP-3,加载上下限值及加载幅值见表 1,目的是确定栓钉连接件的疲劳寿命;3)非完全疲劳破坏试验,即在进行一定次数的疲劳循环后完成静态破坏. 包括5个试件,编号为SFCP-1、SFCP-2、SFCP-3、SFCP-4、SFCP-5,加载上下限值、加载幅值及加载循环次数见表 1,表中疲劳荷载幅值是通过公路钢结构桥梁设计规范[12]中栓钉循环200万次对应的疲劳强度设计值占栓钉抗剪承载力的比例(ΔP/Pu=0.25)给出. 图 2给出了试验加载过程及测试设备.
| 表 1 栓钉推出试验结果 Table 1 Test results of stud push-out specimens |

|
图 2 试件加载过程及测试设备 Figure 2 The specimen loading process and test equipment |
在推出试验中,由于混凝土与栓钉的相对强度等级不同,试件的破坏模式一般分为两类:一是栓钉剪断破坏,二是混凝土发生局部压碎或劈裂. 本次试验采用了C50高强混凝土,3组推出试验结果均表现为栓钉剪断破坏,混凝土翼板除了栓钉根部有局部压碎之外,其整体性仍然很好,且表面未发现裂缝,破坏形态如图 3所示.

|
图 3 推出试件破坏形态 Figure 3 Failure modes of the specimens |
3组栓钉推出试验的结果列于表 1. 由表 1可知,第1组的3个栓钉静力推出试件的极限承载力值较为接近,相对误差不超过4%,其均值为280.8 kN. 第2组疲劳试验结果的离散性相对较大,其中FCP-2试件由于在加载过程中发生侧向偏载,导致试件提前破坏,因而其结果不予采用. 仅取FCP-1和FCP-3的试验结果均值作为推出试件的疲劳寿命,其值为2.68×106. 从第3组非完全疲劳破坏试验的结果看出,在相同疲劳加载幅值作用下,随着疲劳加载次数的增加,推出试件的承载力下降明显.
2 栓钉剩余承载力退化规律 2.1 既有栓钉连接件剩余强度模型目前,栓钉连接件的剩余强度计算模型主要有两种. 第1种认为栓钉的剩余强度与其自身疲劳寿命呈线性退化关系,如Oehlers[13]提出的计算公式为
| ${{P}_{\text{s}}}={{P}_{\text{u}}}\left( 1\frac{n}{N} \right).$ | (1) |
式中:Ps为栓钉连接件剩余承载力;Pu为栓钉连接件极限承载力;n为疲劳荷载循环次数;N为栓钉连接件疲劳寿命.
第2种计算模型认为栓钉的剩余强度与其自身疲劳寿命呈非线性退化关系,如文献[14-15]提出的计算公式为
| $\begin{align} & \frac{{{P}_{\text{s}}}}{{{P}_{\text{u}}}}=0.74\cdot \frac{P\max }{{{P}_{\text{u}}}}\cdot \left( 1\frac{\Delta P}{P\max } \right)+0.54 \\ & 0.04\cdot \ln \left( \frac{n}{10\frac{1P\max {{P}_{\text{u}}}^{1}}{^{0.126\text{ }70.134\text{ }4\cdot P\max \cdot {{P}_{\text{u}}}^{{{1.}_{\left( 10.5\Delta P\cdot {{P}^{1}}_{max} \right)}}}}}n} \right). \\ \end{align}$ | (2) |
式中:Ps为栓钉连接件剩余承载力;Pu为栓钉连接件极限承载力;ΔP为疲劳荷载幅值;n为疲劳荷载循环次数.
以往试验表明,在疲劳荷载作用下,栓钉连接件的剩余承载力在初期退化得很慢,后期越来越快,是一个非线性的过程.可见,式(1)的线性退化描述并不十分合理. 式(2)虽为非线性,但其形式过于复杂,不便于工程应用.
2.2 基于剩余强度理论的栓钉剩余承载力退化模型鉴于在实际工程中,栓钉连接件多认为其为结构构件而非材料,故对其描述为承载力更为贴切. 本文提出栓钉剩余承载力的概念,并基于材料剩余强度理论,旨在建立适用于栓钉连接件在疲劳荷载作用下的剩余承载力计算模型及方法.
2.2.1 材料剩余强度模型
材料的剩余强度R(n)通常是指结构在承受一定荷载循环次数后还具有的抵抗外荷载的能力,它不仅与荷载的循环次数n有关,还与加载的应力水平S
| $R\left( n \right)=f\left( n,S \right).$ | (3) |
对于金属材料,在疲劳加载初期,疲劳荷载作用下产生的缺陷(如位错、滑移、空洞等)对材料的强度影响很小,其剩余强度退化的很慢;但在后期,特别当疲劳循环次数比接近1时,由于材料内部不断萌生的裂纹及其扩展过程引起有效承载面积减少,导致材料剩余强度迅速减小,直至发生破坏.
剩余强度退化曲线有如下特征:1)R(0)=σb,即剩余强度的初始值R(0)等于材料的静力极限强度σb. 2)R(N)=σmax,当剩余强度R(N)等于疲劳荷载峰值σmax时,材料发生破坏,此时的循环次数即为疲劳寿命N. 3)$\frac{dR\left( n \right)}{dn}{{|}_{n\to 0}}\to 0$,即疲劳加载刚开始作用时强度退化得很慢. 4)在n→N时,具有“突然死亡”的特点.
满足上述特性1)、2)的函数一般可写为
| $R\left( n \right)=R\left( 0 \right)R\left( 0 \right){{\sigma }_{\max }}f\left( \frac{n}{N} \right).$ | (4) |
上述特性3)、4)由函数$f\left( \frac{n}{N} \right)$的特性决定,$f\left( \frac{n}{N} \right)\in \left[ 0,1 \right]$.
从研究对象的尺度上划分,目前已有的剩余强度模型可分为宏观唯象模型和微观机理模型. 微观机理模型的原理是从材料内部微观损伤的萌生开始,建立一个精确数值解,然而这类模型仍处于理论研究阶段,这些模型仍以根据经验和试验数据建立的宏观唯象模型居多. 在众多唯象模型中,文献[17]提出的如下剩余强度幂指数退化模型,因其形式简单合理、含义明确而被应用较多.
| $R\left( n \right)=R\left( 0 \right)\left( R\left( 0 \right){{\sigma }_{max}} \right){{\left( \frac{n}{N} \right)}^{c}}.$ | (5) |
对于栓钉连接件而言,其承载力正比于其材料强度,即Ps∝R.参照式(5)剩余强度幂指数退化模型,可得
| ${{P}_{\text{s}}}\left( n \right)=k\left[ R\left( 0 \right)\left( R\left( 0 \right){{\sigma }_{\max }} \right){{\left( \frac{n}{N} \right)}^{c}} \right].\text{ }$ | (6) |
令kR(0)=A,kσmax=B,则有
| ${{P}_{\text{s}}}\left( n \right)=A\left( AB \right){{\left( \frac{n}{N} \right)}^{c}}.$ | (7) |
式中:c为材料常数,且c>1;系数A和B可由边界条件确定.
当n=0时,表示栓钉连接件的剩余承载力为其静力初始值,即Ps(0)=Pu=A,Pu为栓钉承载能力极限值;当n=N时(N为栓钉疲劳寿命),表示栓钉剩余承载力已达到临界破坏状态,此时Ps(n)=Pmax=A-(A-B),Pmax为疲劳荷载上限值,由此可得,B=Pmax.
将A、B代入式(7),得到栓钉承载力的指数退化模型为
| ${{P}_{\text{s}}}\left( n \right)={{P}_{\text{u}}}{{P}_{\text{u}}}{{P}_{\max }}{{\left( \frac{n}{N} \right)}^{c}}.$ | (8) |
为便于后续试验数据统一分析和拟合,对式(8)进行无量纲化处理,即在公式左右两边同时除以栓钉的极限承载力Pu,并记λ=Ps/Pu,α=Pmax/Pu,β=n/N,则有退化模型的无量纲形式为
| $\lambda \left( n \right)=1\left( 1\alpha \right){{\beta }^{c}}$ | (9) |
通过文献调研,对非完全疲劳破坏的栓钉连接件推出试验进行整理总结,按下述原则进行筛选:1)推出试件尺寸是参考Eurocode4中规定的标准推出试件尺寸;2)栓钉连接件的布置方式为焊接;3)试验在常温下进行;4)加载方式为单向加载,疲劳加载频率为3~6 Hz;5)试件破坏模式为栓钉剪断.
根据筛选试验结果,并加上本文的试验数据,共计27个栓钉的推出试验数据列于表 2、3. 表 2数据用于模型拟合,表 3数据用于模型验证,表 2的数据来源为Oehlers试验、Hanswille试验和本文试验,Oehlers试验和Hanswille试验是目前提出两个主流退化模型的数据依托,表 3数据为其他学者完成的试验.
| 表 2 用于拟合的栓钉连接件剩余承载力试验数据 Table 2 Test data of the residual bearing capacity of stud connectors used for fitting |
| 表 3 用于验证的栓钉连接件剩余承载力试验数据 Table 3 Test data of the residual bearing capacity of stud connectors used for verification |
同时为了使不同尺寸、不同疲劳寿命、不同承载能力的栓钉连接件试验数据具有统一性和可比性,对栓钉连接件的疲劳寿命和剩余承载力进行了数据归一化处理. 由此可以得到以α为变量的几组栓钉连接件抗剪承载力退化数据.
根据栓钉连接件剩余承载力模型的物理意义可知,当n=0时,Ps=Pu;当n=N时,Ps=Pmax. 因此对于每组拥有不同的α的试验数据,均有β=0,λ=1;β=1,λ=α. 可见式(9)的定义域为[0,1],值域为[α,1].
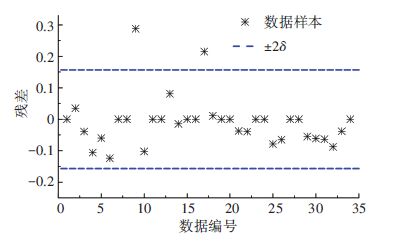
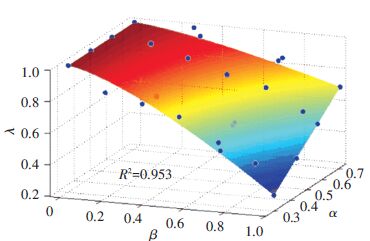
由表 2试验数据并结合模型的物理意义,用MATLAB软件对式(9)进行关于双变量的曲面拟合以确定模型参数c的数值. 为提高拟合精度,在模型初次拟合(R2=0.834)后,根据数据残差以正负两倍标准差±2δ为界剔除离群值,如图 4所示. 之后进行二次拟合,得到模型拟合的决定系数R2=0.953,说明拟合效果较好,此时c=1.34. 图 5为模型曲面拟合结果,于是有
| $\lambda \left( n \right)=1\left( 1\alpha \right){{\beta }^{1.34}}$ | (10) |
| ${{P}_{\text{s}}}\left( n \right)={{P}_{\text{u}}}\left( {{P}_{\text{u}}}{{P}_{\max }} \right){{\left( \frac{n}{N} \right)}^{1.34}}.$ | (11) |
|
图 4 数据残差分析 Figure 4 Residual analysis of data |
|
图 5 模型曲面拟合结果 Figure 5 The fitting results of model surface |
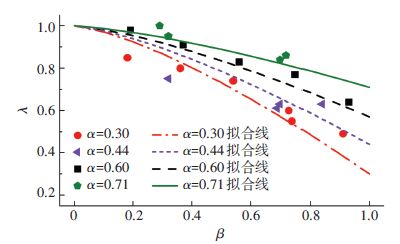
图 6给出了用式(10)画出的拟合曲线与表 1试验数据的对比结果. 从图 6可以看出,在不同的α值情况下,试验值与拟合曲线的趋势和吻合性均较好. 同时可以发现,栓钉承载力随疲劳荷载次数的退化规律曲线呈先慢后快的特点,以α=0.3的退化曲线为例,前20%疲劳寿命中,承载力退化程度仅为8.0%,而最后20%的疲劳寿命,承载力退化度高达18.1%,为前者的2.3倍.
|
图 6 对应不同α的拟合结果 Figure 6 Fitting results of different α |
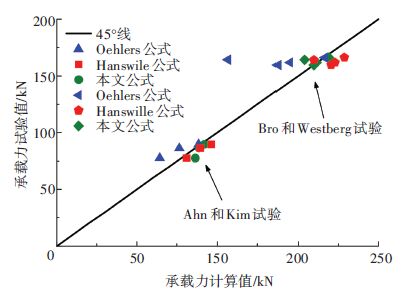
为验证本文提出的幂指数退化模型的正确性及普适性,将本文所提公式的计算结果与表 3栓钉连接件剩余承载力试验数据进行对比,同时与式(1)、(2)的结算结果进行比较,结果见图 7. 由图 7可知,本文公式和Hanswille公式的计算值与试验值吻合较好,而Oehlers公式的计算结果与试验值偏离较大.
|
图 7 疲劳加载后栓钉剩余承载力的计算值与试验值对比 Figure 7 Comparison on calculated and tested values of residual bearing capacity of studs under fatigue loading |
由于表 3的验证数据仍然偏少,为进一步比较和验证3个公式的普适性,现将本文中所有的试验结果与公式计算结果作比对,列于表 4. 同时,将表 4中3个公式的计算值与试验值的比值进一步统计分析,计算其平均值、标准差和变异系数得到:Oehlers公式的均值为0.64,方差为0.26,离散系数为0.40;Hanswille公式的均值为1.08,方差为0.17,离散系数为0.16;本文公式的均值为0.99,方差为0.08,离散系数为0.08.
| 表 4 栓钉剩余承载力试验值与计算值对比结果 Table 4 Comparison on calculated and tested values of residual bearing capacity of studs |
由此可知,Oehlers公式的均值最小,仅为0.64,可见其计算结果误差较大;Hanswille公式的均值大于1,表明其公式计算结果偏于不安全,且其离散系数为0.16,说明公式的稳定性相对较差. 本文公式的试验值与计算值之比的均值为0.99,离散系数也仅为0.08,说明本文的公式不仅误差较小,且稳定性好. 可见,本文提出的幂指数退化模型可以较好地描述栓钉连接件的剩余承载力随疲劳循环次数的变化规律.
3 结 论1) 在疲劳荷载作用下,栓钉连接件的抗剪承载力随疲劳循环次数发生退化. 通过栓钉推出试件的3组试验(静载破坏试验、完全疲劳试验以及非完全疲劳破坏试验)再次验证了退化现象.
2) 为使不同加载条件下的非完全疲劳破坏的栓钉连接件推出试验数据具有统一性和可比性,对栓钉连接件的疲劳寿命和剩余承载力进行了数据归一化处理,并通过两次双变量参数拟合剔除个别离群值,提高了拟合精度.
3) 在疲劳荷载作用下,栓钉连接件的剩余承载能力呈现先慢后快的非线性退化趋势. 所提出的栓钉连接件承载力幂指数退化模型形式简单合理、适用性强、稳定性好,可以较好地描述栓钉连接件的剩余承载力随疲劳循环次数的变化规律,相关文献的试验数据也验证了该模型的正确性.
| [1] |
黄侨.
桥梁钢-混凝土组合结构设计原理[M]. 北京: 人民交通出版社, 2004 .
HUANG Qiao. Design principle of steel-concrete composite bridge structures[M]. Beijing: China Communications Press, 2004 . (  0) 0)
|
| [2] |
荣学亮, 黄侨, 任远. 栓钉连接件锈蚀后静力性能和抗疲劳性能的试验研究[J].
土木工程学报,2013, 46 (2) : 10-18.
RONG Xueliang, HUANG Qiao, REN Yuan. Experimental study on static and fatigue behaviors of stud connectors for composite beams after corrosion[J]. China Civil Engineering Journal,2013, 46 (2) : 10-18. (  0) 0)
|
| [3] |
聂建国, 谭英, 王洪全. 钢-高强混凝土组合梁栓钉剪力连接件的设计计算[J].
清华大学学报(自然科学版),1999, 39 (12) : 94-97.
NIE Jianguo, TAN Ying, WANG Hongquan. Design and calculation of stud shear connectors in steel-high strength concrete composite beams[J]. Journal of Tsinghua University (Natural Science),1999, 39 (12) : 94-97. (  0) 0)
|
| [4] |
蔺钊飞, 刘玉擎. 焊钉连接件峰值滑移及剪力-滑移本构关系[J].
同济大学学报(自然科学版),2014, 42 (7) : 1006-1010.
DOI: 10.3969/j.issn.0253-374x.2014.07.003 LIN Zhaofei, LIU Yuqing. Peak slip and load-slip realationship of headed stud connectors[J]. Journal of Tongji University (Natural Science),2014, 42 (7) : 1006-1010. DOI: 10.3969/j.issn.0253-374x.2014.07.003 (  0) 0)
|
| [5] |
王宇航, 聂建国. 基于断裂力学的组合梁栓钉疲劳性能[J].
清华大学学报(自然科学版),2009, 49 (9) : 1467-1470.
WANG Yuhang, NIE Jianguo. Fatigue behavior of studs in a composite beam based on fracture mechanics[J]. Journal of Tsinghua University,2009, 49 (9) : 1467-1470. (  0) 0)
|
| [6] |
MAINSTON R J. Shear connectors in steel-concrete composite beams for bridges and the new C. P. 117 part 2[J].
Composite Materials,1967, 38 (9) : 323-329.
( 0) 0)
|
| [7] |
RODERICK J W, ANSOURIAN P. Repeated loading of composite beams[J].
Institution of Engineers (Australia) Civil Engineering Transactions,1976, 18 (2) : 109-116.
( 0) 0)
|
| [8] |
OEHLERS D J, COUGHLAN C G. The shear stiffness of stud shear connections in composite beams[J].
Journal of Constructional Steel Research,1986, 6 (4) : 273-284.
DOI: 10.1016/0143-974X(86)90008-8 ( 0) 0)
|
| [9] |
OEHLERS D J, FOLEY L. The fatigue strength of stud shear connections in composite beams[J].
Proceedings of the Institution of Civil Engineers Part Research & Theory,1985, 79 (2) : 349-364.
( 0) 0)
|
| [10] |
薛伟辰, 罗子文, 王骅. 周期荷载下栓钉连接件的抗剪性能试验研究[J].
哈尔滨工业大学学报,2005, 37 (9) : 372-375.
XUE Weichen, LUO Zihua, WANG Hua. Experimental studies on behavior of stud shear connectors subjected to cyclic loads[J]. Journal of Harbin Institute of Technology,2005, 37 (9) : 372-375. (  0) 0)
|
| [11] |
European Committee for Standardisation. Eurocode 4 design of composite steel and concrete structures, part 2: bridge[S]. London: BSI, 2007.
( 0) 0)
|
| [12] |
公路钢结构桥梁设计规范:JTG D64—2015[S].北京:人民交通出版社, 2015.
Specifications for design of highway steel bridge:JTG D64—2015[S]. Beijing: China Communications Press, 2015. (  0) 0)
|
| [13] |
OEHLERS D J. Deterioration in strength of stud connectors in composite bridge beams[J].
Journal of Structural Engineering,1989, 116 (12) : 3417-3431.
( 0) 0)
|
| [14] |
HANSWILLE G, PORSCH M, USTUNDAG C. Resistance of headed studs subjected to fatigue loading part I: experimental study[J].
Journal of Constructional Steel Research,2007, 63 (4) : 475-484.
DOI: 10.1016/j.jcsr.2006.06.035 ( 0) 0)
|
| [15] |
HANSWILLE G, PORSCH M, USTUNDAG C. Resistance of headed studs subjected to fatigue loading part II: analytical study[J].
Journal of Constructional Steel Research,2007, 63 (4) : 485-493.
DOI: 10.1016/j.jcsr.2006.06.036 ( 0) 0)
|
| [16] |
姚卫星.
结构疲劳寿命[M]. 北京: 国防工业出版社, 2003 .
YAO Weixing. The fatigue life of structure[M]. Beijing: National Defence Industry Press, 2003 . (  0) 0)
|
| [17] |
SCHAFF J R, DAVIDSON B D. Life predict ion methodology for composite structures: part I-constant amplitude and two-stress level fatigue[J].
Journal of Composite Materials,1997, 31 (2) : 128-157.
DOI: 10.1177/002199839703100202 ( 0) 0)
|
| [18] |
XIE E. Fatiguestrength of shear connectors[R]. Guimar es: University of Minho, 2011.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


