磁浮列车具备安全舒适、绿色环保、噪声和污染小等性能,是客运交通运输现代化的重要标志[1]. 而中低速磁浮列车更以其低噪声、低能耗、线路适应性强及线路成本低等优点成为城市内部有竞争力的新型公共交通工具[2]. 准确的电机参数对电机控制和建模意义重大,与旋转感应电机相比,直线感应电机的机械气隙较大,通常情况下励磁电感相比于等容量的旋转感应电机小很多[3]. 直线感应电机的初级绕组嵌于槽内,次级常采用无槽的铝铁复合次级,使得直线感应电机的初级和次级漏感差别较大,直线电机是磁浮列车重要的工作部件,而且是依靠直线感应电机来实现列车的牵引与制动的,但如何能对直线电机快速选型及电机参数的计算是至关重要的[4]. 其动态特性和结构可靠性对车辆有直接影响,有必要对其动态特性进行研究. 同时,磁浮列车为电磁悬浮,对其动态参数控制有严格要求,为增大载重及提高列车运行可靠性,本文对其结构进行有限元分析,对其开展中低速磁浮列车的悬浮控制具有重要意义[5].
1 中低速磁浮SLIM定型设计约束条件 1.1 SLIM的基本参数要求由于应用环境、位置、空间和条件的约束,SLIM的几个主要定型参数已经是确定的,它们分别是电机额定线电压U=220 V;电机设计长度L=1 800~2 000 mm;电机次级为铝-铁复合结构,铝板厚4 mm,铁轭厚度20 mm;电机机械气隙13 mm,电磁气隙δ=17 mm;电机宽不大于560 mm,电机铁心高85 mm.
1.2 SLIM容量与最大工作电流选择从运行的可靠性角度出发,同类SLIM在额定点附近(40 km/h)效率大约为50%,功率因数大约为0.57,在40 km/h时电机的牵引功率为36 kW,故牵引电机的容量确定为
$S=\frac{P}{\eta \cdot cos~\varphi }=\frac{36\text{ }000}{0.50\times 0.57}\approx 126~\text{kVA}.$
式中: η和cos φ分别为额定点电机的效率、功率因数.选择SLIM容量为130 kVA,则最大工作电流为
$I=\frac{S}{\sqrt{3}U}=\frac{130\text{ }000}{\sqrt{3}\times 220}=341~\text{A}.$
因此SLIM的最大工作电流设计为340 A,额定频率f=39.4 Hz.
2 SLIM的快速参数定型过程1) 给定设计的基本参数:设计的初级线负荷约为As=84 000 A/m,设计的气隙磁通密度约为B=0.18T,设计的每极每相槽数q1=3,绕组节距为y=8.
2) 根据车底安装空间限制,确定电机的长度范围,这样可以预先确定电机的极数和极距参数. 技术流程如下:设实际的电机极数为2P,则有效长度范围内的虚拟极数为2P+1,极距的范围计算为
$\tau =\frac{L}{2P+1}=\frac{1\text{ }800~\text{mm}}{9}\tilde{\ }\frac{2\text{ }000~\text{mm}}{9}=200\tilde{\ }222~\text{mm}.$
因为电机设计相数m1=3,每极每相槽数q1=3,故取一个能被9整除的数值,即τ=207 mm和216 mm,此时分别对应2P=9(9为虚拟极数,实际有效极数8个)和2P=8,然后根据以下修正的槽数Z的计算公式,可得Z=2P·m1·q1+y,即8极的Z=80,8极的Z=89. 如表 1所示的两种可选设计方案,并分别定义型号为M-1和M-2.
| 表 1 SLIM两种可选设计方案 Table 1 Two optional designs of SLIM |
根据齿距[6]计算公式${{t}_{1}}=\frac{\tau }{{{m}_{1}}{{q}_{1}}}$,可得M-1的齿距为24 mm,M-2的齿距为23 mm.
3)初级绕组导线选型及参数
计算根据最大工作电流选择导线的截面积:A=Ist/J,电机初级允许最大工作电流Ist=340 A,根据成本要求,选择铝材质导线,其单位面积电流量为J=3~4 A/mm2. 因此导线截面积最小为A=340/4=85 mm2. 选择导线线规18.5 mm×5.2 mm,则导线截面积A=96.2 mm2>85 mm2.
此时推算电机的最大线负荷为
${{A}_{\text{s}}}=Z\cdot 2N\cdot {{I}_{\text{st}}}/L.$
每槽导体数计算${{N}_{\text{c}}}=\frac{N\text{ph}}{P\prime {{q}_{1}}}$,式中$P\prime $为等值极对数,当P为偶数时,取$P\prime $=P;当P为奇数时,取$P\prime $=(2P-1)/2,因此,M-1型和M-2型都可计算得到Nc=6=2×3,式中Nph=72,因为采用双层叠绕的方式,因此槽内导体布局为两层,每一层3根. 相关技术数据见表 2所示.
| 表 2 SLIM两种可选设计方案 Table 2 Two optional designs of SLIM |
4) 槽型选择和参数计算
计算初级绕组导体总宽15.6 mm. 当导体线圈用0.1 mm聚酰亚胺带绕两层后,总的槽宽bs为16.8 mm. 根据M-1和M-2的齿距分别计算齿宽bt:M-1齿宽为7.2 mm,M-2齿宽为6.2 mm,计算初级绕组导体总高为37 mm. 取槽楔高h0是3 mm,考虑各层间绝缘厚度,故槽深h0+h1=40.8 mm. 取槽深为41.0 mm. 计算初级铁轭高Hy=44 mm.
当电机槽型选为开口槽时,如图 1所示,得各参数对照如表 3所列.

|
图 1 SLIM槽型及结构尺寸 Figure 1 Groove profile and structure size of SLIM |
| 表 3 SLIM两种可选设计方案槽参数设计 Table 3 Groove parameters design for SLIM’s two optional designs |
5) 初级绕组特性计算[7]
绕组分布系数${{k}_{\text{p}}}=\frac{\sin \frac{\pi }{2{{m}_{1}}}}{{{q}_{1}}\sin ~\pi \frac{2}{{{m}_{1}}{{q}_{1}}}}$,绕组短距系数${{k}_{\text{d}}}=sin(\frac{\pi }{2}\frac{y}{{{m}_{1}}{{q}_{1}}})$,绕组系数kw1=kdkp.
再考虑绕组的“缩减系数”${{\alpha }_{\text{w}}}=\frac{2P1.5}{2P1}$,初级铁心宽为
$D=\frac{\pi \cdot S}{2\times 4.44{{\alpha }_{\text{w}}}\cdot B\cdot AS\cdot {{\tau }^{2}}f\cdot 2P\cdot {{k}_{\text{w}1}}}.$
初级每极磁通$\phi =\frac{2}{\pi }B\tau D$,电机初级每相串联匝数${{N}_{\text{ph}}}=\frac{{{k}_{\text{e}}}{{U}_{1}}}{4.44f\phi {{k}_{\text{w}1}}}$,其中ke为反电势系数,取值0.52,U1为相电压,取值$220~\text{V}/\sqrt{3}=127\text{V}$. 初级绕组特性相关参数对照见表 4.
| 表 4 SLIM两种可选设计方案初级绕组参数特性 Table 4 Two optional design parameter characteristics of SLIM primary winding |
6)SLIM的磁路计算[8]
实际气隙磁通${{\phi }_{\text{m}}}=\frac{{{k}_{\text{e}}}{{U}_{1}}}{4.44f{{N}_{\text{ph}}}{{k}_{w1}}}$,气隙磁通密度${{B}_{\delta }}=\frac{\pi {{\phi }_{\text{m}}}}{2\tau D}$,齿磁通密度${{B}_{\text{t}}}={{B}_{\delta }}\frac{{{t}_{1}}}{{{k}_{\text{fe}}}{{b}_{\text{t}}}}$,其中kfe是铁心压装系数,kfe=0.93. 初级铁轭磁通密度${{B}_{\text{y}}}=\frac{{{\phi }_{\text{m}}}}{{{k}_{\text{fe}}}D({{H}_{\text{y}}}\frac{2}{3}{{H}_{\text{d}}})}$,其中Hy即初级铁轭高44 mm,Hd为固紧孔直径,取10 mm.气隙系数${{\delta }_{e}}=\frac{{{t}_{1}}}{{{t}_{1}}\frac{{{b}^{2}}_{0}}{5\delta +{{b}_{0}}}}\cdot \delta $,等效气隙${{\delta }^{\prime }}_{\text{e}}={{k}_{\delta 2}}{{\delta }_{\text{e}}}$,气隙磁路特性相关参数对照见表 5.
| 表 5 SLIM两种可选设计方案气隙磁路参数特性 Table 5 Air gap magnetic circuit parameter characteristics for SLIM’s two optional designs |
7) 电机磁势计算
气隙磁势${{F}_{\delta }}=1.6\times {{10}^{6}}{{B}_{\delta }}{{\delta }^{\prime }}_{\text{e}}$,初级齿磁势Ft=2Htht,查磁化曲线得Ht=240 A/m. 初级轭磁势${{F}_{\text{y}}}=\xi {{H}_{\text{a}}}\tau $,其中ξ为磁通密度分布不均匀的系数,取ξ=0.7,查磁化曲线得Ha=285 A/m. 一对磁极的总磁势降(忽略了次级铁心的磁势降)$\sum{F={{F}_{\delta }}}+{{F}_{\text{a}}}+{{F}_{\text{t}}}$,磁路饱和系数${{k}_{\mu }}=\frac{\Sigma F}{{{F}_{\delta }}}$,磁化电流${{I}_{\mu }}=\frac{P\cdot \Sigma F}{0.9{{m}_{1}}{{N}_{\text{ph}}}{{k}_{\text{w}1}}}$,电机磁势相关参数对照为表 6.
| 表 6 SLIM两种可选设计方案电机磁势参数特性 Table 6 Motor magnetic potential parameter characteristics for SLIM’s two optional designs |
8) 等值电路计算
绕组端部长Le=1.4τ,绕组半匝平均长Lcp=D+Le+0.03,初级每相电阻${{r}_{1}}=\frac{{{\rho }_{\text{AL}}}\cdot 2{{L}_{\text{cp}}}\cdot {{N}_{\text{ph}}}}{A}$,初级导线为铝材质,电阻率为ρAL=2.95×10-8. 槽漏磁导${{\lambda }_{\text{s}}}={{k}_{\text{u}}}\frac{{{h}_{0}}}{{{b}_{\text{s}}}}+{{k}_{\text{k}}}\frac{{{h}_{1}}}{3{{b}_{\text{s}}}}$,查表可知ku=0.916 7,kk=0.937 5.齿端漏磁导${{\lambda }_{\text{t}}}=\frac{3\cdot \frac{y}{{{m}_{1}}{{q}_{1}}}+1}{4}\times \frac{5\frac{\delta }{{{b}_{0}}}}{5+4\frac{\delta }{{{b}_{0}}}}$,初级绕组端部漏磁导${{\lambda }_{\text{e}}}=0.34\frac{{{q}_{1}}}{D}({{L}_{\text{e}}}0.64\frac{y}{{{m}_{1}}{{q}_{1}}}\tau ){{k}^{2}}_{\text{p}}$,谐波漏磁导${{\lambda }_{\text{d}}}=\frac{{{t}_{1}}{{k}_{\text{w}1}}^{2}}{12{{\delta }^{\prime }}_{\text{e}}{{k}_{\mu }}}[1+{{k}_{\beta }}{{(\frac{{{m}_{1}}{{q}_{1}}}{5})}^{2}}]$,kβ是与短距有关的系数,查表得kβ=0.028 1,kμ=1.01. 磁化电抗${{x}_{\text{m}}}=\frac{4{{m}_{1}}}{\pi {{k}_{\mu }}}{{\mu }_{0}}\frac{{{\left( {{N}_{ph}}{{k}_{w1}} \right)}^{2}}}{P\cdot {{\delta }^{\prime }}_{\text{e}}}Df\tau $,气隙磁场基波漏抗${{x}_{\delta }}=(\frac{\cosh \frac{\pi {{g}^{\prime }}_{\text{e}}}{\tau }}{\cosh \frac{\pi {{g}^{\prime }}_{\text{e}}}{2\tau }}1){{x}_{\text{m}}}$,初级每相漏抗
${{x}_{1}}=\frac{15.8\cdot f}{100}{{(\frac{{{N}_{\text{ph}}}}{100})}^{2}}\frac{D}{{{q}_{1}}p}[{{\lambda }_{\text{s}}}+{{\lambda }_{\text{t}}}+{{\lambda }_{\text{e}}}+{{\lambda }_{\text{d}}}]+{{x}_{\delta }}.$
SLIM的品质因数计算为$G=\frac{2{{\mu }_{0}}f{{\tau }^{2}}\cdot d}{\pi {{\delta }^{\prime }}_{e}\cdot {{\rho }_{\text{AL}}}}$, 起动参数:${{r}_{\text{e}0}}=\frac{sG}{1+{{\left( sG \right)}^{2}}}{{x}_{\text{e}0}}=\frac{1}{1+{{\left( sG \right)}^{2}}}$,起动时,滑差s=1,c=0.01,查表得参数:kp=2.027,kq=9.37,Da=-0.011 2,Dj=0.007 09,Dfa= -0.020 59,Dfj=0.016 47.
$\begin{align} & {{r}_{\text{e}}}={{r}_{\text{e}0}}{{k}_{p}}[1+(\frac{{{D}_{\text{a}}}{{D}_{\text{j}}}{{k}_{\text{q}}}}{sG{{k}_{\text{p}}}})]{{x}_{\text{m}}} \\ & {{x}_{\text{e}}}={{x}_{\text{e}0}}{{k}_{q}}[1+({{D}_{\text{a}}}+sG{{D}_{\text{j}}}\frac{{{k}_{\text{p}}}}{{{k}_{\text{q}}}})]{{x}_{\text{m}}}, \\ & {{r}_{\text{ef}}}={{r}_{\text{e}0}}{{k}_{p}}[1+({{D}_{\text{fa}}}\frac{{{D}_{\text{fj}}}{{k}_{\text{q}}}}{sG{{k}_{\text{p}}}})]{{x}_{\text{m}}}. \\ \end{align}$
初级绕组磁导相关参数见表 7.
| 表 7 SLIM两种可选设计方案磁导参数特性 Table 7 Magnetic conductance parameter characteristics for SLIM’s two optional designs |
9) 起动特性计算
初级回路电流为
${{I}_{\text{st}}}=\frac{{{U}_{1}}}{\sqrt{{{({{r}_{1}}+{{r}_{\text{e}}})}^{2}}+{{({{x}_{1}}+{{x}_{\text{e}}})}^{2}}}}.$
起动功率因数为
$\cos \varphi =\frac{{{r}_{1}}+{{r}_{\text{e}}}}{\sqrt{{{({{r}_{1}}+{{r}_{\text{e}}})}^{2}}+{{({{x}_{1}}+{{x}_{\text{e}}})}^{2}}}}.$
起动感应电势${{E}_{1}}={{I}_{\text{st}}}\sqrt{{{r}^{2}}_{\text{e}}+{{x}^{2}}_{\text{e}}}$,校核反电势系数ke=E1/U1,与设定值0.52相差很小. 起动推力由电机经过气隙传递到次级的同步有功功率与初级输入有效功率平衡关系决定[9],也即
${{F}_{\text{st}}}=\frac{{{m}_{1}}{{I}_{\text{st}}}{{E}_{1}}}{2\tau f}\cdot \cos ~\varphi .$
启动相关特性参数对照见表 8.
| 表 8 SLIM两种可选设计方案起动特性参数特性 Table 8 Starting parameter characteristics for SLIM’s two optional deisgns |
从表 8可以看出,M-2型电机比M-1型启动电流大,功率因素高,启动推力高21.3%.
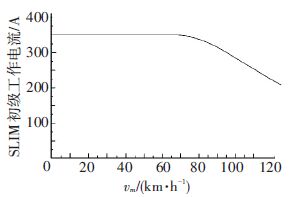
3 输出外特性测试两种备选设计方案所涉及的SLIM能否满足中低速范围内牵引制动特性要求,是必然要进行相关测试加以验证的. 结合感应电机的运行原理可知在SLIM高速运行区域,随着初级绕组感生电动势的增加,初级电流会出现下垂特性[10-11],如图 2所示. 在SLIM稳态的T-型等效电路模型中这部分是无法直观描述的,对此本文结合目前国内外相关设计测试资料[12],为获得SLIM优良控制性能,SLIM初级电流与电机速度的变化特性为SLIM初级电流有效值在时速>60 km/h以后会有下垂特性,这与实际运行工况相符合.
|
图 2 备选设计方案SLIM的工作电流-速度特性 Figure 2 The current-speed characteristics of SLIM |
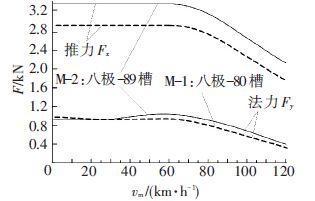
图 3给出的是通过国内外相关资料并结合此前设计计算方案获得的SLIM功率因数的特性图[13]. 由图 3可知,备选的八极-89槽SLIM设计方案比八极-80槽SLIM设计方案在电机功率因数和效率上都要稍高一些,如图 4所示,因此该方案各方面的性能表现更好.

|
图 3 备选设计方案SLIM的计算功率因数-速度特性 Figure 3 Power factor-speed characteristics of SLIM |
|
图 4 备选设计方案SLIM的推力(Fx)法向力(Fy)有限元计算-速度特性 Figure 4 英文标题 |
电流-滑差控制特性下两种设计方案下电机的推力输出特性[14]:
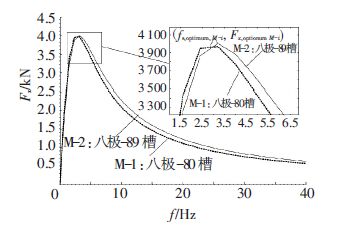
1) 第1种是在恒定的额定电流340 A工况下,当滑差频率从零变化到额定频率,也即0~39.4 Hz过程中,电机的推力输出特性如图 5所示.
|
图 5 推力输出与滑差频率的变化特性 Figure 5 Variation characteristics of thrust output and slip frequency |
由图 5可知:一是电机工作在法向力最优点滑差频率推力输出可以满足单台SLIM的牵引控制要求;二是获得在推力峰值点的推力最优点滑差推力峰值点. 其中,推力最优点滑差频率及其峰值力的计算可直接通过SLIM的T-模型获得
$\begin{align} & {{f}_{\text{s},\text{optimum},\text{M}-i}}=\frac{{{R}_{\text{s},\text{M}-i}}}{2\pi ({{L}_{\text{m},\text{M}-i}}+{{L}_{ls,\text{M}-i}})} \\ & {{F}_{x,\text{optimum},\text{M}-i}}=\frac{3\pi }{2\tau }\cdot \frac{{{L}^{2}}_{\text{m},\text{M}-i}}{({{L}_{\text{m},\text{M}-i}}+{{L}_{ls,\text{M}-i}})}\cdot {{I}^{2}}_{\text{p}}. \\ \end{align}$
结合前面设计参数,并由互感参量计算式为
${{L}_{\text{m}}}=\frac{2{{m}_{1}}}{{{\pi }^{2}}{{k}_{\mu }}}{{\mu }_{0}}\frac{{{({{k}_{\text{w}1}}{{N}_{\text{ph}}})}^{2}}}{P\cdot {{\delta }^{\prime }}_{\text{e}}}\times D\tau ,$
次级等效电阻计算式[15]为
${{R}_{\text{s}}}=\frac{2{{m}_{1}}{{\rho }_{\text{AL}}}{{({{k}_{\text{w}1}}{{N}_{\text{ph}}})}^{2}}}{P}\times \frac{D}{d\cdot \tau }.$
次级漏感简化计算式为
${{L}_{\text{ls}}}\approx \frac{\tau {{\mu }_{0}}d}{2\pi \kappa {{\rho }_{\text{AL}}}}\cdot \frac{{{\sinh }^{2}}(2\kappa {{\delta }^{\prime }}_{\text{e}})}{{{\sinh }^{2}}(\kappa {{\delta }^{\prime }}_{\text{e}})\cdot \sinh \left( 2\kappa d \right)}\cdot {{R}_{\text{s}}}.$
得到最终简化的最优点3个控制参数Lm、Rs、Lls,如表 9所示.
| 表 9 SLIM两种可选设计方案控制相关动态参数精确计算 Table 9 Precise calculation for controlling dynamic parameters of SLIM’s two optional designs |
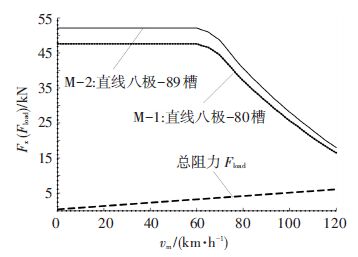
2) 第2种是在恒定的法向力最优点控制滑差频率13.69 Hz下,当电机初级电流有效值从启动到额定值并考虑到高速区感生电动势增强致电流下垂的特性,电机的推力输出特性如图 6所示.
|
图 6 频率13.69 Hz下两种设计方案牵引特性验证 Figure 6 Traction characteristic verification of two designs at 13.69 Hz |
由图 6可知,即使考虑了高速区电流的下垂特性,在法向力最优点恒定滑差频率13.69 Hz下,采用两种电机设计方案的整个磁浮列车牵引力输出都高于15 kN,完全在列车所受总阻力之上,也即两种设计方案都能够满足120 km/h中低速范围内的牵引要求. 从图 6中也可以发现,八极-89槽(M-2型)备选方案的SLIMs(30台同时工作)相比八极-80槽(M-1型)的SLIMs(30台同时工作)在整体牵引力输出上要高出约10%,尤其是当SLIM设计在额定运行工况30~40 km/h时,M-2型设计方案要优于M-1型设计方案,对磁浮牵引能力的提升很有帮助. 当然,本设计方案还仅仅是考虑SLIM电机的机械气隙为17 mm悬浮前的牵引力设计要求,若考虑磁浮列车处于悬浮稳定的工况下,此时SLIM的机械气隙约8 mm,这样电机的推力特性曲线会至少抬升20%~ 30%.
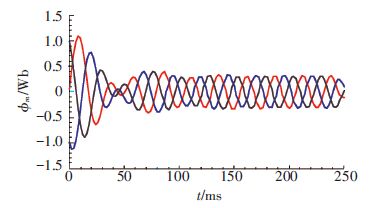
4 有限元仿真测试结果两个备选方案的电机,但是对于SLIM的实际推力和法向力测试比较困难,因为当SLIM处于运行的过程中时,其推力和法向力的测试也必须是动态跟随的,因此是有一定的困难,不过,借助Ansoft/ maxwell可以近似了解两种设计方案的优劣性,可以采用有限元仿真的方法在同一工作条件、环境及材料属性下对比验证两个方案的力特性,恒滑差频率取为13.69 Hz,仿真计算结果统计如图 7~8所示. 从实验结果可以看出,M-2型比M-1型不论是低速区还是中高速区输出的推力都要高约16%,此外由于取电机在悬浮气隙8 mm下,两者的法向力输出约为300~600 N,但M-2在中高速区法向力输出相比M-1型约少了12%.
|
图 7 八极-89槽SLIM初级感应磁链特性 Figure 7 Primary induction flux characteristics of 8 pole-89 slot SLIM |

|
图 8 两种方案下的SLIM恒电流恒滑差频率输出特性对比 Figure 8 Output characteristic contrast of the slip-frequency |
观察图 8所示的两种SLIM设计方案输出特性可知:八极-89槽电机输出推力为(3200±50)N,比八极-80槽电机高约23%(理论计算值为16%),而初级铁芯在参考法向y轴所受法向力约为-800 N左右,与八极-80槽电机所受法向力相差不大. 整体来说,备选八极-89槽SLIM虽然增加了小的成本,但换取了电机较大的性能提升.
图 9给出的是中低速磁悬浮列车用8极-80槽SLIM安装布局示意. 经过现场的牵引制动测试后发现既有的SLIM方案基本满足此前的设计要求. 考虑到设计、工艺制造成本及条件的限制,八极(虚拟9极)-89槽的SLIM并非现场加工制作出来,不过通过前面的理论计算与有限元仿真验证,表明了该方案的可行性,对提升磁浮SLIM的整体性能很有帮助.

|
图 9 单转向架试验小车SLIM及悬浮电磁铁布局 Figure 9 Electromagnet layout of the single bogie |
1) 从满足中低速磁浮用SLIM的牵引制动特性要求出发给出了两种直线电机的备选设计方案,一种是八极-80槽长度1 927 mm,一种是八极-89槽长度2 047 mm,此两种直线电机在磁悬浮转向架安装上都能满足长宽高上空间尺寸的要求.
2) 在结构空间、材料成本酌优考量的基础上,给出一种SLIM快速定型设计的方法,对SLIM的绕组极数、节距、匝数、槽型、布线等的快速准确定型.
3) 对两种SLIM设计方案分别进行了磁路计算、磁势计算、等值电路计算、起动特性计算等,并给出相应的计算对比结果. 从设计计算结果可知,八极-89槽备选方案不论是在启动推力,还是在功率因数电机效率上都优于八极-80槽直线电机.
4) 8极-80槽SLIM已经量产化,其性能测试与理论计算和有限元仿真相差较小,8极(虚拟9极)-89槽SLIM虽未量产化,但其整体性能在理论和仿真实验上都予以了验证,是一种优化的可行方案.
| [1] |
YAN L. Development and application of the maglev transportation system[J].
IEEE Transactions on applied Superconductivity,2008, 18 (2) : 92-99.
DOI: 10.1109/TASC.2008.922239 ( 0) 0)
|
| [2] |
XU W, ZHU J G, ZHANG Y, et al. An improved equivalent circuit model of a single-sided linear induction motor[J].
IEEE Transactions on Vehicular Technology,2010, 59 (5) : 2277-2289.
DOI: 10.1109/TVT.2010.2043862 ( 0) 0)
|
| [3] |
LU Q, LI Y, SHEN X, et al. Analysis of linear induction motor applied in low-speed maglev train [C]// Proc 15th International Conference on Electrical Machines and Systems. Hokkaido, Sapporo: IEEE Press, 2012: 1-6.
( 0) 0)
|
| [4] |
KUIJPERS A A, NEMLIOGLU C, SAHIN F, et al. Force analysis of linear induction motor for magnetic levitation system [C]// Proc 14th International IEEE Power Electronics and Motion Control Conference. Ohrid: IEEE Press, 2010: 17-20.
( 0) 0)
|
| [5] |
SHIRI A, SHOULAIE A. Design optimization and analysis of single-sided linear induction motor,considering all phenomena[J].
IEEE Transactions on Energy Conversion,2012, 27 (2) : 516-525.
DOI: 10.1109/TEC.2012.2190416 ( 0) 0)
|
| [6] |
TAKAHASHI I, IDE Y. Decoupling control of thrust and attractive force of a LIM using a space vector control inverter[J].
IEEE Transactions on Industry Applications,1993, 29 (1) : 161-167.
DOI: 10.1109/28.195902 ( 0) 0)
|
| [7] |
AHN JR S C, LEE J H, HYUN D S. Dynamic characteristic analysis of LIM using coupled FEM and control algorithm[J].
IEEE Transactions on Magnetics,2000, 36 (4) : 1876-1880.
DOI: 10.1109/20.877811 ( 0) 0)
|
| [8] |
魏凯.基于低速磁悬浮列车的直线感应电机的控制研[D].成都:西南交通大学,2007.
WEI Kai. Control of low-speed maglev train based linear induction motor [D]. Chengdu: Southeast Jiaotong University, 2007. (  0) 0)
|
| [9] |
WAI R J, CHU C C. Motion control of linear induction motor via petri fuzzy neural network[J].
IEEE Transactions on Industrial Electronics,2007, 54 (1) : 281-295.
DOI: 10.1109/TIE.2006.885475 ( 0) 0)
|
| [10] |
MARINO R, PERESADA S, VALIGI P. Adaptive input-output linearizing control of induction motors[J].
IEEE Transactions on Automatic Control,1993, 38 (2) : 208-221.
DOI: 10.1109/9.250510 ( 0) 0)
|
| [11] |
CHEN S L, LIN K H. A slim RFID tag antenna design for metallic object applications[J].
IEEE Antennas and Wireless Propagation Letters,2008, 7 : 729-732.
DOI: 10.1109/LAWP.2008.2009473 ( 0) 0)
|
| [12] |
LEE I O, CHO S Y, MOON G W. Improved phase-shift PWM converter for larger sized PDP slim sustain power module[J].
IEEE Transactions on Power Electronics,2013, 28 (2) : 945-958.
DOI: 10.1109/TPEL.2012.2202251 ( 0) 0)
|
| [13] |
PETROVIC V, ORTEGA R, STANKOVIC A M, et al. Design and implementation of an adaptive controller for torque ripple minimization in PM synchronous motors[J].
IEEE Transactions on Power Electronics,2000, 15 (5) : 871-880.
DOI: 10.1109/63.867676 ( 0) 0)
|
| [14] |
KIM K, LIM S, PARK N C, et al. Structural dynamics modification of slim optical disk drive[J].
IEEE Transactions on Magnetics,2009, 45 (5) : 2209-2212.
DOI: 10.1109/TMAG.2009.2016151 ( 0) 0)
|
| [15] |
MOON H R, SHIN M H, LEE J Y, et al. Design of integrated light guide plate with functional structure of enhanced diffusion length for ultra-slim LED backlight unit[J].
Journal of Display Technology,2015, 11 (1) : 44-52.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


