CFRP加固钢结构界面间的早期剥离破坏常发生在CFRP的粘结端,这种破坏的发生决定了此项加固技术的成败. 工程技术人员对CFRP端部采用不同的锚固方式来阻止CFRP端部早期剥离破坏. 如文献[1]通过试验研究了U型箍锚固量和锚固方式对加固梁承载力的影响. 文献[2-5]通过试验提出了通过机械紧固的方法,但研究机械锚固法存在施工麻烦、易腐蚀和费用较高等缺点. 文献[6]利用角钢和螺栓在FRP板端部锚固来阻止了FRP板的剥离. 上述研究成果大多都是通过试验研究CFRP端部锚固的意义. 但CFRP的端部被锚固后,CFRP端被封盖住,属于隐蔽构造,故很难通过试验手段准确地测量出端部胶层的剪应力和CFRP拉应变分布情况.
在理论上,文献[7]根据滑移理论建立了端部压条锚固时的胶层粘结剪应力模型,解释了CFRP压条锚固的力学机理. 而很少有人从CFRP端部锚固程度的强弱出发,在力学行为上定量解析出CFRP端部被锚固后的胶层剪应力规律及端部抗剪强度提高程度. 目前只有部分学者[8-10]利用数值模拟的手段指出了设置U型锚固后加固梁的剥离承载力将得到提高. 文献[10]也对U型箍的锚固效果进行了数值模拟,指出了U型箍能防止剥离破坏,但会引起受力不均匀. 目前工程中也大量采用U型箍锚固方法,但关于不同的U型锚固形式对加固梁承载力的影响程度还不清楚. 本文针对上述情况,建立了CFRP端部无锚固、完全锚固以及一端锚固一端不锚固等不同边界条件下的粘结胶层剪应力模型,比较了这几种端部不同锚固条件下及不同锚固程度时端部CFRP的受拉和胶层受剪的分布规律,并进行了相应参数的定量分析,为CFRP加固钢结构的端部锚固设计提供了借鉴.
1 CFRP端部不同锚固时的力学模型 1.1 基本假定为真实研究CFRP锚固端的受力,采用以下假定:1)CFRP、钢结构、粘结胶层均为理想的弹性体. 2)由于CFRP与钢结构粘结界面间胶层厚度较薄,粘结界面间的胶层仅承受剪切力,发生剪切变形. 3)当粘贴多层CFRP时,各分层CFRP间的胶层也仅发生剪切变形,设各分层CFRP间胶层的应变传递系数为α,最外面第1分层CFRP应变为εf1(x),则第2分层CFRP应变为εf2(x)=α·εf1(x),第i分层CFRP应变为εfi(x)=α(i-1)·εf1(x). 层数n≥1,此时x截面位置处的所有CFRP层的平均应变为
| $\begin{align} & {{\varepsilon }_{f}}\left( x \right)=\varepsilon _{f}^{1}(x)+\varepsilon _{f}^{2}(x)+\ldots +\varepsilon _{f}^{n}\left( x \right)n= \\ & \frac{\varepsilon _{f}^{1}(x)\cdot \left[ 1+\alpha +\ldots +{{\alpha }^{(n-1)}} \right]}{n}. \\ \end{align}$ |
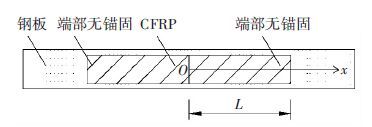
各分层CFRP间胶层的应变传递系数(0 <α<1)与胶层的材料参数、厚度等因素有关. 4)CFRP端L截面处,CFRP端拉应变εf(L)与该处的钢结构的拉应变εs(L)满足:εf(L)=β·εs(L),其中β为CFRP端部锚固程度系数(0≤β<1). 当CFRP端部处未被锚固时,如图 1所示,CFRP端部处的应变为0,此时β=0. 当CFRP端部被锚固时,如图 2所示,CFRP端部处的应变值不为0,此时根据锚固程度强弱确定β值. 需要指出β不能为1,如果β为1,表明CFRP端部与钢结构完全同步变形,但在实际情况中不会出现这种情况,因此β∈[0,1),β值越大,锚固程度越大.
|
图 1 CFRP加固钢拉伸构件示意 Figure 1 The diagram of CFRP reinforcing steel tension |

|
图 2 CFRP两端均锚固示意图 Figure 2 The diagram of anchoring both ends of CFRP |
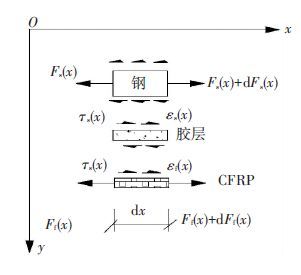
取图 1中CFRP加固钢板拉伸试件为研究对象. 由于整个模型是对称的,取试件中心的位置为O点. 以微段dx为研究对象,其受力如图 3所示.
|
图 3 微段受力状态 Figure 3 The force diagram of micro-segment |
图 3中: Fs、Ff分别为钢板、单侧CFRP端部承受的拉力;Fs(x)、Ff(x)分别为钢板、单侧CFRP x处截面受的拉力; τs(x)、εs(x)分别为钢板界面x处剪应力、拉应变;τf(x)、εf(x)分别为CFRP界面x处剪应力、应变;σf(x)为x处CFRP拉应力;te、tf、ts分别为胶层、CFRP、钢板厚度;bf、bs分别为CFRP、钢板截面宽度. 粘贴多层CFRP时,εf(x)、σf(x)为x截面位置处的全部CFRP层的平均值,此时tf为全部CFRP层的总厚度.
1.3 平衡方程的建立根据单元受力图,可建立CFRP及胶层平衡方程为
| ${{\tau }_{f}}(x)=\frac{~{{t}_{f}}d{{\sigma }_{f}}(x)}{dx},$ | (1) |
| ${{\tau }_{f}}(x)=G{{\gamma }_{xy}}\left( x \right)$ | (2) |
式中G为胶层剪切模量,γxy(x)为胶层x处剪应变.
设在荷载作用下,CFRP表面点x处发生的位移量为(u,v),通过对式(1)、(2)整理得
| $\frac{{{d}^{2}}{{\sigma }_{f}}(x)}{d{{x}^{2}}}=\frac{G}{{{t}_{f}}}\frac{~{{d}^{2}}u}{dxdy}+\frac{{{d}^{2}}v}{{{d}^{2}}x}~.$ | (3) |
由于胶层厚度很薄,沿其厚度方向的弹性压缩变形很小,可近似将v值视为0,因此式(3)可以简化为
| $\frac{{{d}^{2}}{{\sigma }_{f}}(x)}{d{{x}^{2}}}=\frac{G}{{{t}_{f}}~}\frac{{{d}^{2}}u}{dxdy}.$ | (4) |
由图 2可知
| $\frac{{{d}^{2}}u}{dxdy}=\frac{{{\varepsilon }_{f}}(x)-{{\varepsilon }_{s}}(x)}{{{t}_{e}}}.$ | (5) |
则式(4)可以整理为
| $\frac{~{{d}^{2}}{{\sigma }_{f}}(x)}{d{{x}^{2}}}=\frac{G}{{{t}_{f}}}\frac{{{\varepsilon }_{f}}(x)-{{\varepsilon }_{s}}(x)}{{{t}_{e}}}.$ | (6) |
其中:Es为钢板弹性模量,Ef为CFRP的弹性模量,εs(x)=σs(x)Es,εf(x)=σf(x)Ef.
由于
| ${{F}_{s}}\left( x \right)=F-2{{F}_{f}}\left( x \right)$ | (7) |
| ${{F}_{s}}\left( x \right)={{t}_{s}}{{b}_{s}}{{\sigma }_{s}}(x),$ | (8) |
| ${{F}_{f}}\left( x \right)={{t}_{f}}{{b}_{f}}{{\sigma }_{f}}(x).$ | (9) |
因此
| ${{\sigma }_{s}}(x)=\frac{F-2{{F}_{f}}\left( x \right)}{{{t}_{s}}{{b}_{s}}}=\frac{F-2{{t}_{f}}{{b}_{f}}{{\sigma }_{f}}(x)}{{{t}_{s}}{{b}_{s}}}.$ | (10) |
通过式(7)~(10)可以将式(9)整理为
| $\frac{{{d}^{2}}{{\sigma }_{f}}(x)}{d{{x}^{2}}}-\frac{G}{{{t}_{f}}{{t}_{e}}{{E}_{f}}}+\frac{2G{{b}_{f}}}{{{t}_{s}}{{t}_{e}}{{b}_{s}}{{E}_{s}}}{{\sigma }_{f}}(x)+\frac{FG}{{{t}_{f}}{{t}_{e}}{{t}_{s}}{{b}_{s}}{{E}_{s}}}=0.$ | (11) |
对式(11)进行求解,得
| ${{\sigma }_{f}}(x)={{C}_{1}}{{e}^{\sqrt{Ax}}}+{{C}_{2}}{{e}^{-\sqrt{Ax}}}+\frac{B}{A},$ | (12) |
| ${{\tau }_{f}}(x)=({{C}_{1}}\sqrt{A}{{e}^{\sqrt{Ax}}}-{{C}_{2}}\sqrt{A}{{e}^{-\sqrt{Ax}}}){{t}_{f}},$ | (13) |
| ${{\varepsilon }_{f}}(x)=\frac{{{C}_{1}}{{e}^{\sqrt{Ax}}}+{{C}_{2}}{{e}^{-\sqrt{Ax}}}+B/A}{{{E}_{f}}}.$ | (14) |
其中
| $\begin{align} & A=\frac{G}{{{t}_{f}}{{t}_{e}}{{E}_{f}}}+\frac{2G{{b}_{f}}}{{{t}_{s}}{{t}_{e}}{{b}_{s}}{{E}_{s}}} \\ & B=\frac{FG}{{{t}_{f}}{{t}_{s}}{{t}_{e}}{{b}_{s}}{{E}_{s}}}, \\ \end{align}$ |
当粘贴多层(n≥1)CFRP时,则根据基本假设可以推导出第i层的CFRP应变表达式为
| $\varepsilon _{f}^{i}(x)=\frac{{{\varepsilon }_{f}}(x)\cdot n\cdot {{\alpha }^{(i-1)}}}{\left[ 1+\alpha +\ldots +{{\alpha }^{(n-1)}} \right]}.$ | (15) |
根据基本假设可知,端部截面处的CFRP拉应变与钢板拉应变关系为
| ${{\varepsilon }_{f}}(L)=\beta {{\varepsilon }_{s}}(L).$ | (16) |
式中L为拉伸试件表面中心到CFRP端部截面处的长度.
根据图 3,有
| $F=2{{\varepsilon }_{f}}(L){{t}_{f}}{{b}_{f}}{{E}_{f}}+{{\varepsilon }_{s}}(L){{t}_{s}}{{b}_{s}}{{E}_{s}}.$ | (17) |
因此可以求得CFRP端部截面处的拉应力为
| ${{\sigma }_{f}}(L)=\frac{F-\frac{F{{E}_{s}}{{t}_{s}}{{b}_{s}}}{2{{t}_{f}}{{b}_{f}}{{E}_{f}}\beta +{{t}_{s}}{{b}_{s}}{{E}_{s}}}}{2{{t}_{f}}{{b}_{f}}}.$ | (18) |
观察式(18)中可以发现:当β=0时,σf(L)=0,此时CFRP端部截面没被锚固;当σf(L)≠0时,CFRP端部被锚固,σf(L)值的大小由锚固程度系数决定.
1.4.2 CFRP两端均不锚固边界条件当CFRP两端均不锚固时,取锚固系数β=0,根据图 1能建立如下边界条件:
| $\left\{ \begin{align} & x=0,{{\tau }_{f}}(0)=0; \\ & x=L,{{\sigma }_{f}}(L)=0. \\ \end{align} \right.$ |
则可求得系数C1、C2为
| ${{C}_{1}}={{C}_{2}}=\frac{-\frac{B}{A}}{{{e}^{\sqrt{AL}}}+{{e}^{-\sqrt{AL}}}}$ |
CFRP两端均锚固时,根据锚固程度强弱来确定锚固系数和图 2,能建立如下边界条件:
| $\left\{ \begin{align} & x=0,{{\tau }_{f}}(0)=0; \\ & x=L,{{\sigma }_{f}}(L)=\frac{\left( F-\frac{{{E}_{s}}{{t}_{s}}{{b}_{s}}F}{2{{A}_{f}}{{E}_{f}}\beta +{{t}_{s}}{{b}_{s}}{{E}_{s}}} \right)}{2{{A}_{f}}}. \\ \end{align} \right.$ |
则可求得系数C1、C2为
| ${{C}_{1}}={{C}_{2}}=\frac{\left( F-\frac{\frac{{{E}_{s}}{{t}_{s}}{{b}_{s}}F}{2{{A}_{f}}{{E}_{f}}\beta +{{t}_{s}}{{b}_{s}}{{E}_{s}}}}{2{{A}_{f}}} \right)-\frac{B}{A}}{{{e}^{\sqrt{AL}}}+{{e}^{-\sqrt{AL}}}}.$ |
当CFRP一端锚固、一端未锚固时,未锚固端的CFRP锚固系数β=0;锚固端根据锚固程度强弱来确定锚固系数β值. 根据图 4能建立如下边界条件:
| $\left\{ \begin{align} & x=L,{{\sigma }_{f}}(L)=\frac{\left( F-\frac{{{E}_{s}}{{t}_{s}}{{b}_{s}}F}{2{{A}_{f}}{{E}_{f}}\beta +{{t}_{s}}{{b}_{s}}{{E}_{s}}} \right)}{2{{A}_{f}}}, \\ & x=-L,{{\sigma }_{f}}(-L)=0. \\ \end{align} \right.$ |
则可求得系数C1与C2为
| $\left\{ \begin{align} & {{C}_{1}}=\frac{\frac{B}{A}{{e}^{-2\sqrt{AL}}}+\left( \frac{F-\frac{{{E}_{s}}{{t}_{s}}{{b}_{s}}F}{2{{A}_{f}}{{E}_{f}}\beta +{{A}_{s}}{{E}_{s}}}}{2{{A}_{f}}} \right)-\frac{B}{A}}{{{e}^{\sqrt{AL}}}-{{e}^{-3\sqrt{AL}}}}; \\ & {{C}_{2}}=\frac{\frac{B}{A}{{e}^{-2\sqrt{AL}}}-\left( \frac{F-\frac{{{E}_{s}}{{t}_{s}}{{b}_{s}}F}{2{{A}_{f}}{{E}_{f}}\beta +{{t}_{s}}{{b}_{s}}{{E}_{s}}}}{2{{A}_{f}}} \right)}{{{e}^{-2\sqrt{AL}}}-\frac{B}{A}{{e}^{\sqrt{AL}}}-{{e}^{-3\sqrt{AL}}}}. \\ \end{align} \right.$ |
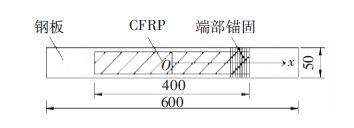
为验证所建立的理论模型的正确性,根据试验方案[11]进行对比计算. 试验钢板选用Q235钢,CFRP厚度为0.167 mm. 试验对CFRP一端采用横向缠绕式锚固,另一端CFRP未锚固,加固试件尺寸如图 4所示.
|
图 4 试件尺寸图(mm) Figure 4 The chart of specimen size (mm) |
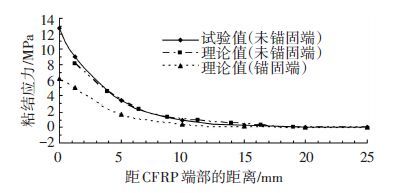
图 5为拉伸荷载为90 kN时,界面间胶层的粘结剪应力曲线. 观察发现,由于图 4中左端CFRP端部未锚固,故计算时取左端的锚固系数β=0,此时计算得到在试验第1测点处(虚线位置处)的未锚固端处胶层的粘结剪应力为12.68 MPa,而通过试验得到的粘结剪应力为8.1 MPa,二者仅相差0.91 MPa,计算精度达到了91%,并且理论曲线与试验曲线的其他部位也吻合得很好. 同时图 6中所示的CFRP端部拉应变曲线也吻合得很好,表明文中所建立的粘结胶层剪应力公式和CFRP拉应变计算公式是正确的,可用来研究CFRP端部锚固后的粘结剪应力问题.
|
图 5 界面间胶层剪应力曲线 Figure 5 The shear stress curve of interface between rubber |
另外图 4中CFRP右端部采用了缠绕式锚固,由于锚固端粘贴方式复杂,很难通过试验准确地测到锚固端部区域胶层的剪应力和CFRP拉应变分布情况. 但利用文中建立的计算公式能够得到锚固区域胶层剪应力和CFRP的拉应变分布情况. 如图 5、6中的理论值(锚固端)曲线. 观察发现,对CFRP端部锚固后,端部区域胶层中的粘结剪应力值下降到6.20 MPa,下降达到了50%,同时锚固端部CFRP的拉应变为679 με,达到了中间区域最大拉应变的50%.
可见对CFRP端部锚固后,CFRP端部处胶层的剪应力降低,缓解了端部胶层中剪应力集中现象,CFRP端部的早期剥离破坏也能有效避免. 同时端部的CFRP能更好地与钢板协调受力,端部区域CFRP的利用效率也得到了提高.
|
图 6 CFRP拉应变曲线 Figure 6 The tensile strain curve of CFRP |
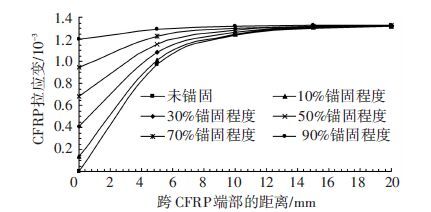
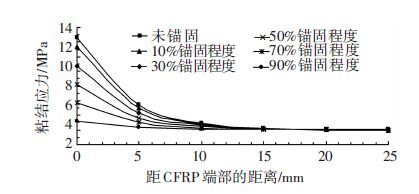
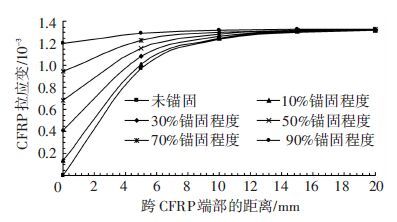
为了研究CFRP端部锚固程度的强弱对CFRP端部胶层粘结剪应力及端部CFRP受拉的影响情况,分别研究了锚固程度系数为0、10%、30%、50%、70%、90%时的胶层粘结剪应力和CFRP拉应变分布情况. 如图 7、8所示. 观察图 7发现,采用不同锚固系数时的胶层粘结剪应力依次为12.68、11.36、8.76、6.20、3.69、1.21 MPa. 粘结剪应力值依次降低的比例依次为10.4%、30.9%、51.1%、70.9%、90.5%. 可见,粘结剪应力降低的大小与锚固程度提高的比例值相同. 即:CFRP端部锚固程度越高,CFRP端部处的胶层受剪程度越低,越不容易发生破坏;同时端部处CFRP的受拉程度也越大. 因此在实际工程中,应该对CFRP端部进行高强度的锚固.
|
图 7 不同锚固程度时剪应力曲线 Figure 7 The shear stress curve under different anchoring degree |
|
图 8 不同锚固程度时CFRP拉应变曲线 Figure 8 The strain curve of CFRP under different anchoring degree |
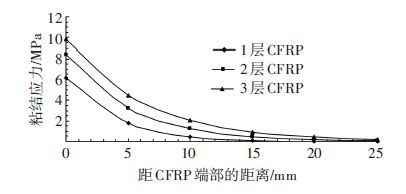
图 9、10分别为在相同荷载作用时,端部锚固、端部不锚固情况下分别粘贴1层、2层、3层CFRP时胶层中粘结剪应力曲线. 可以看出:CFRP端部锚固后,粘贴1层、2层、3层CFRP时胶层中的粘结剪应力分别为6.20、8.40、9.88 MPa;在CFRP端部不锚固条件下的胶层中的粘结剪应力分别为12.68、17.56、21.07 MPa. 根据以上结果发现,拉伸条件下:1)随着CFRP层数的增加,CFRP端部胶层中的粘结剪应力会逐渐增大;2)CFRP端部被锚固后,胶层粘结剪应力要比端部不被锚固后的粘结剪应力降低.
|
图 9 端部锚固的粘结剪应力曲线 Figure 9 The bonding shear stress curve without end anchorage |

|
图 10 端部不锚固的粘结剪应力曲线 Figure 10 The bonding shear stress curve without end anchored |
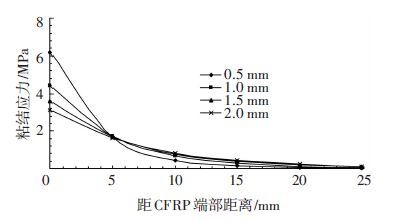
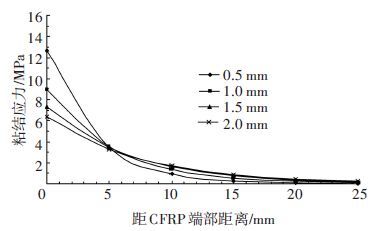
图 11、12分别为在相同荷载作用时,端部锚固、端部不锚固情况下胶层粘结厚度分别为0.5、1.0、1.5、2.0 mm时的胶层粘结剪应力曲线. 可以看出:CFRP端部锚固条件下,胶层粘结厚度分别为0.5、1.0、1.5、2.0 mm时胶层粘结剪应力分别为6.20、4.38、3.58、3.10 MPa;在CFRP端部不锚固条件下的粘结剪应力分别为12.68、8.96、7.32、6.34 MPa. 可见如果胶层厚度较薄,并且端部不进行锚固时,CFRP端部的早期剥离破坏必然会发生.
|
图 11 端部锚固时的粘结剪应力曲线 Figure 11 The bonding shear stress curve under end anchorage |
|
中文注解 图 12 端部不锚固时的粘结剪应力曲线 Figure 12 The bonding shear stress curve without end anchored |
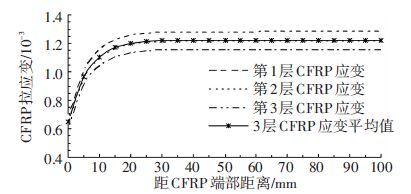
图 13、14分别为端部锚固条件下粘贴3层CFRP时,胶层的应变传递系数不同时的各分层CFRP的应变分布曲线(胶层递系数分别取0.95、0.6). 观察发现,第1分层(最外层) CFRP受拉程度最大,第3分层(最内层) CFRP受拉程度最小,而第2分层(中间层)居中,第2分层的拉应变值也是最接近所有CFRP层的平均受拉程度. 另外,当CFRP层间胶层的应变传递系数越大时,各分层CFRP受拉程度越接近,各分层CFRP能很好地实现共同受力;当CFRP分层间胶层的应变传递系数越小时,各分层CFRP的受拉程度则相差较大,各分层CFRP几乎不能共同受力,并且最里层的CFRP承担很小的拉力. 可见,当粘贴多层CFRP时,要选择各分层CFRP间的胶层传递系数大的粘结剂,这样能保证多层CFRP共同、均匀受力,使多层CFRP的加固效果最佳,此时各分层的CFRP利用效率最高.
|
图 13 各分层CFRP应变曲线(α=0.95) Figure 13 The CFRP strain curve of every layer(α=0.95) |

|
图 14 各分层CFRP应变曲线(α=0.6) Figure 14 The CFRP strain curve of every layer(α=0.6) |
1) 建立了CFRP端部锚固、不锚固等几种边界条件下的CFRP加固钢板拉伸构件的界面应力模型,定量地分析了端部锚固程度强弱对端部胶层受剪和CFRP受拉的影响规律,并对各参数变化后所导致的界面粘结剪应力的影响规律进行了分析.
2) 相比端部不锚固的情况,CFRP端部被锚固处的胶层中的剪应力降低,CFRP的拉应力增大. 并且锚固程度越高,CFRP端部处胶层的受剪程度越低,其剪应力降低的大小与端部锚固程度提高的值相同. 因此在实际工程中,应该对CFRP端部进行高强度的锚固.
3) 粘贴多层CFRP时,应选择各分层CFRP间的胶层传递系数大的粘结剂,这样能保证多层CFRP共同、均匀受力. 另外,CFRP端部锚固后,减少CFRP层数、增加胶层厚度,胶层中的剪应力会降低.
4) 端部锚固程度系数的选取对CFRP端部胶层中的剪应力分布至关重要,文中的端部锚固系数是按照一定比例关系选取的. 在后续研究中,将根据文中的理论公式,并开展U型箍锚固、钢板压条锚固、机械锚固等不同锚固方式的端部锚固系数的试验研究,给出各种锚固方式下的端部锚固系数值.
| [1] |
李伟文, 严志亮, 曹征良, 等. 混凝土粗糙度对CFRP与混凝土粘结性的影响[J].
深圳大学学报,2007, 24 (1) : 13-17.
LI Weiwen, YAN Zhiliang, CAO Zhengliang, et al. Effect of concrete roughness on the adhesion of CFRP and concrete[J]. Journal of Shenzhen University,2007, 24 (1) : 13-17. (  0) 0)
|
| [2] |
WU Yufei, HUANG Yue. Hybrid bonding of FRP to reinforced concrete structures[J].
Journal of Composites for Constructions,2008, 12 (3) : 266-273.
DOI: 10.1061/(ASCE)1090-0268(2008)12:3266 ( 0) 0)
|
| [3] |
PELLEGRINO C, MODENA C. Flexural strengthening of real scale RC and PRC beams with end anchored pretensioned FRP laminates[J].
ACI Structural Journal,2009, 6 (16) : 319-328.
( 0) 0)
|
| [4] |
阎卫国, 张宇峰, 吴宇飞. FRP粘贴锚固系统性能研究[J].
公路,2010 (12) : 26-31.
YAN Weiguo, ZHANG Yufeng, WU Yufei. Study on the performance of FRP bond anchorage system[J]. Highway,2010 (12) : 26-31. (  0) 0)
|
| [5] |
崔熙光, 刘智, 刘项, 等. 碳纤维加固混凝土构件端部锚固试验研究[J].
工业建筑,2011, 41 (7) : 125-128.
DOI: 10.13204/j.gyjz2011.07.027 CUI Xiguang, LIU Zhi, LIU Xiang, et al. Experimental study on the end anchorage of the concrete members strengthened with CFRP[J]. Industrial Construction,2011, 41 (7) : 125-128. DOI: 10.13204/j.gyjz2011.07.027 (  0) 0)
|
| [6] |
GALAL K, MOFIDI A. Strengthening RC beams in flexure using new hybrid FRP sheet ductile anchor system[J].
Journal of Composites for Construction,2009, 13 (3) : 217-225.
DOI: 10.1061/(ASCE)CC.1943-5614.0000006 ( 0) 0)
|
| [7] |
张子潇, 叶列平, 陆新征. U型FRP加固钢筋混凝土梁受剪剥离性能的有限元分析[J].
工程力学,2005, 22 (4) : 155-162.
ZHANG Zixiao, YE Lieping, LU Xinzheng. Finite element analysis of shear behavior of RC beams strengthened with U shaped FRP sheets[J]. Engineering Mechanics,2005, 22 (4) : 155-162. (  0) 0)
|
| [8] |
周朝阳, 谭磊, 程小念. FRP抗剪加固钢筋混凝土梁研究综述[J].
建筑科学与工程学报,2011, 28 (2) : 1-7.
ZHOU Chaoyang, TAN Lei, CHENG Xiaonian. Review of research on reinforced concrete beams strengthened with FRP for shear[J]. Journal of Architecture and Civil Engineering,2011, 28 (2) : 1-7. (  0) 0)
|
| [9] |
李保中.锚固压条对CFRP-混凝土截面性能的影响及作用机理研究[D].哈尔滨:哈尔滨工业大学,2012.
LI Baozhong. Study on bonding behaviors and mechanism of the interface between CFRP concrete ending anchored with CFRP strip[D].Harbin: Harbin Institute of Technology,2012. (  0) 0)
|
| [10] |
黄丽华, 王跃方, 李璐. CFRP加固梁U型锚固效果的数值分析[J].
土木建筑与环境工程,2014, 36 (6) : 8-13.
DOI: 10.11835/j.issn.1674-4764.2014.06.002 HUANG Lihua, WANG Yuefang, LI Lu. Finite element analysis of the effects of U wrap anchorages on RC beams strengthenes with CFRP sheets[J]. Journal of Civil Construction and Environmental Engineering,2014, 36 (6) : 8-13. DOI: 10.11835/j.issn.1674-4764.2014.06.002 (  0) 0)
|
| [11] |
彭福明.纤维增强复合材料加固修复金属结构界面性能研究[D].西安:西安建筑科技大学,2005.
PENG Fuming. Research on the interfacial performance of metallic structures strengthened with fibre reinfoeced polymers[D]. Xi’an: Xi’an University of Architecture and Technology,2005. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


