2. 同济大学 桥梁系, 上海 200092 ;
3. 长安大学 公路学院 , 西安 710061
2. Department of Bridge Engineering, Tongji University, Shanghai 200092, China ;
3. School of Highway, Chang’an University, Xi’an 710061,China
斜拉桥是大跨度桥梁的主要桥型之一. 在跨越宽阔的海峡、河流等地形时,传统两塔斜拉桥的跨越能力难以满足要求,建造具有多个主跨的多塔斜拉桥有可能成为技术上经济上更加可行的选择. 但多塔斜拉桥的整体刚度较小,文献[1-2]提出了一种通过增加斜拉索,在主跨跨中设置一个拉索交叉区来提高多塔斜拉桥刚度的措施.
多塔斜拉桥刚度不足的主要原因是中间桥塔缺少锚索的有效约束,两侧也缺少辅助墩,活载作用下桥塔及主梁容易发生较大变形[3]. 一般可通过增大塔梁刚度或增加辅助构件以提高多塔斜拉桥的总体刚度[4-7],如Rion-Antirion Bridge采用了刚度较大的金字塔形桥塔[8];香港汀九桥通过增加稳定索提高了中塔的纵桥向刚度. 嘉绍大桥则采用了调节塔梁刚度,桥塔处设置双排支座,跨中设置刚性铰等措施来提高结构刚度[9]. 增大桥塔刚度是增大多塔斜拉桥刚度最直接的手段,其弊端是活载作用下桥塔要承受巨大的不平衡力,增大了桥塔及下部结构的造价. 在水深较深的河流或海峡,使用跨中交叉索比增大桥塔刚度经济性可能更优. 即将建成的跨越福斯湾三塔斜拉桥两个主跨长度均为650 m,采用了跨中交叉索来提高结构刚度[10].
Gimsing曾对跨中交叉索的作用机理进行过初步论述,认为采用跨中交叉索的多塔斜拉桥是一阶稳定结构,当桥塔产生顺桥向的位移时,被交叉索悬吊的梁段重量通过在交叉索之间的重新分配提供对桥塔的约束作用[11]. 目前,针对跨中交叉索的作用机理研究尚不多见,交叉索对于桥塔的约束作用效果尚不明确. 本文拟建立带交叉索多塔斜拉桥力学模型,推导交叉索纵桥向约束刚度的简化计算公式,并分析交叉索在提高多塔斜拉桥刚度方面所起的作用.
1 理论分析带跨中交叉索的多塔斜拉桥结构形式,如图 1所示.

|
图 1 采用跨中交叉索的多塔斜拉桥立面布置 Figure 1 Side view of multi-span cable-stayed bridge with crossed cables |
本部分主要研究采用跨中交叉索对多塔斜拉桥中塔的纵向约束作用. 研究采用如下基本假定:1)不考虑斜拉索的垂度造成的几何非线性效应,索的弹性模量采用等效弹性模量. 2)活载引起的结构变形较小,不考虑结构变形引起拉索倾角改变. 3)塔梁之间设置纵向约束,活载作用下主梁与桥塔无纵向相对位移. 4)仅考虑拉索对桥塔的纵向约束作用,不考虑主梁抗弯刚度对桥塔纵向刚度的增强作用.
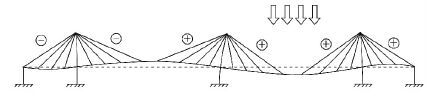
多塔斜拉桥中某一个主跨满布活载而其余主跨空载时,结构变形达到最大,如图 2所示,各跨拉索索力均有所改变,图中“+”表示索力增大,“-”表示索力减小. 外侧桥塔由于锚索的约束作用,变形较小,而中塔的变形主要取决于其自身的抗推刚度、拉索的刚度以及主梁的抗弯刚度.
|
图 2 活载作用下三塔斜拉桥变形 Figure 2 Deformation of triple-tower cable-stayed bridge under live load |
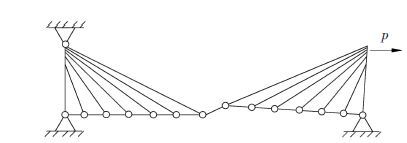
研究多塔斜拉桥中拉索对于桥塔的纵向约束作用时,采用如下方法:选取其中一个主跨及相邻桥塔,约束其中一个桥塔的位移,在另外其中一个桥塔塔顶处施加水平力,如图 3所示,通过研究水平力与塔顶位移的关系,可获得拉索对于桥塔的纵向约束作用. 图 3所示的是传统多塔斜拉桥拉索对桥塔的约束.
|
图 3 拉索的约束作用图示 Figure 3 Restriction effect of the cables |
由图 3可以看出,若不计主梁的抗弯刚度,则拉索对于桥塔几乎无约束作用,此时结构的变形依赖于桥塔本身的抗推刚度.
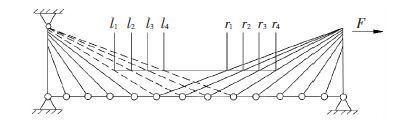
在研究交叉索对桥塔的约束作用时,同样取其中一个主跨,约束左侧桥塔顺桥向位移,在右侧塔顶施加水平力,如图 4所示. 为便于研究,对图 4中交叉索编号,与左侧桥塔相连的交叉索依次为l1、l2、l3、l4,与右侧桥塔相连的交叉索编号为r1、r2、r3、r4.
|
图 4 带交叉拉索的主跨 Figure 4 Main span with crossed cables |
图 4中,跨中部分梁段的重量由左右两侧桥塔的交叉索共同承担. 当右侧塔顶受到图 4所示的水平力作用时,桥塔发生顺时针转动,与右侧塔顶相连的交叉索(r1、r2、r3、r4)被拉伸,跨中梁段的重量更多地分配到右侧交叉索中,导致其索力增大,由此产生对桥塔的约束作用. 由此可见,交叉索对于桥塔的纵向约束来源于所悬吊主梁的重量在两侧交叉索中的重新分配.
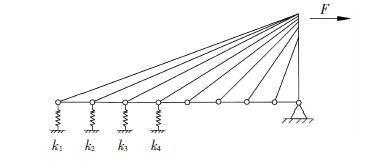
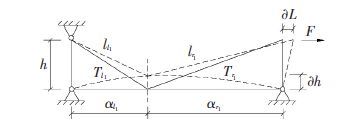
为研究交叉索对桥塔的约束刚度,将与左侧桥塔相连的交叉索(l1、l2、l3、l4)对主梁的竖向支撑简化为竖向的弹簧,如图 5所示,选取图 4中l1、r1一对交叉索进行研究,如图 6所示.
|
图 5 一侧的交叉索等效为弹簧 Figure 5 Crossed cables on one side equivalent to springs |
|
图 6 交叉索变形图示 Figure 6 Deformation of crossed cables |
图 6中,索的长度为l,索的水平投影长度为a,竖直投影长度为h(即桥面以上桥塔高度),索力为T,用下标l1与r1分别表示左侧与右侧交叉索. 首先研究左侧交叉索l1l对于所悬吊梁段的竖向刚度k1.
对于左侧拉索,有
| ${{l}_{{{l}_{1}}}}=\sqrt{{{h}^{2}}+a_{{{l}_{1}}}^{2}}.$ | (1) |
索长对桥塔高度取偏分得
| $\frac{\partial {{l}_{{{l}_{1}}}}}{\partial h}=\frac{h}{\sqrt{{{h}^{2}}+a_{{{l}_{1}}}^{2}}}=\frac{h}{{{l}_{{{l}_{1}}}}}.$ | (2) |
由式(2)可知,当交叉索悬吊的梁段向上提升高度∂h时,左侧交叉索的伸缩量∂ll1量为
| $\partial {{l}_{{{l}_{1}}}}=\frac{h\partial h}{{{l}_{{{l}_{1}}}}}.$ | (3) |
索的伸缩量∂ll1与索力改变量∂Tl1的关系为
| $\partial {{l}_{{{l}_{1}}}}=\frac{\partial {{T}_{{{l}_{1}}}}{{l}_{{{l}_{1}}}}}{E{{A}_{{{l}_{1}}}}},$ | (4) |
式中E、Al1分别为左侧交叉索的弹性模量与横截面积.
由式(3)、(4)可得
| $\frac{h\partial h}{{{l}_{{{l}_{1}}}}}=\frac{\partial {{T}_{{{l}_{1}}}}{{l}_{{{l}_{1}}}}}{E{{A}_{{{l}_{1}}}}}.$ | (5) |
左侧交叉索的索力改变量∂Tl1与竖直分力改变量∂Vl1的关系为
| $\partial {{T}_{{{l}_{1}}}}=\frac{{{l}_{{{l}_{1}}}}}{h}\partial {{V}_{{{l}_{1}}}},$ | (6) |
式中∂Vl1为索力竖直分力的改变量.
将式(6)代入式(5)中可得
| $\frac{~h\partial h}{{{l}_{{{l}_{1}}}}}=\frac{{{l}_{{{l}_{1}}}}^{2}\partial {{V}_{{{l}_{1}}}}}{E{{A}_{{{l}_{1}}}}h}.$ | (7) |
式(7)可转换为
| $\frac{\partial {{V}_{{{l}_{1}}}}}{\partial h}=\frac{E{{A}_{{{l}_{1}}}}{{h}^{2}}}{l_{{{l}_{1}}}^{3}}.$ | (8) |
由式(8)可知,左侧拉索l1的竖向弹簧刚度为
| ${{k}_{1}}=\frac{E{{A}_{{{l}_{1}}}}{{h}^{2}}}{l_{{{l}_{1}}}^{3}}.$ | (9) |
对于右侧交叉索,有
| ${{h}^{2}}+{{a}^{2}}_{{{r}_{1}}}=l_{{{r}_{1}}}^{2}.$ | (10) |
式中lr1为右侧拉索长度,ar1为右侧拉索的水平投影长度.
当右侧施加一个水平力F时,塔顶处水平位移为∂L,水平位移来自于两部分:一部分来自梁段的提升引起的r1的空间位置的改变,另一部分来自索r1的伸长.
首先求解梁段提升引起的右侧塔顶位移. 式(10)中,右侧拉索水平投影长度对塔高求偏分,得
| $\frac{\partial {{a}_{{{r}_{1}}}}}{\partial h}=\frac{-h}{\sqrt{{{l}^{2}}_{{{r}_{1}}}-{{h}^{2}}}}=-\frac{h}{{{a}_{{{r}_{1}}}}}.$ | (11) |
由式(11)可知,梁段提升∂h与塔顶位移∂ar1关系为
| $\frac{\partial {{a}_{{{r}_{1}}}}}{\partial h}=-\frac{h}{{{a}_{{{r}_{1}}}}.}$ | (12) |
由水平力F引起的右侧索力竖向分量为
| $\partial {{V}_{{{r}_{1}}}}=F\frac{h}{{{a}_{{{r}_{1}}}}}.$ | (13) |
由于左侧拉索l1提供的竖向刚度为k1,右侧拉索竖向分力引起的梁段提升为
| $\partial h=\frac{\partial {{V}_{{{r}_{1}}}}}{{{k}_{1}}}.$ | (14) |
式(9)、(13)代入式(14)得
| $\partial h=F\frac{l_{{{l}_{1}}}^{3}}{{{a}_{{{r}_{1}}}}hE{{A}_{{{l}_{1}}}}}.$ | (15) |
式(15)代入式(12)可得梁端提升引起的右侧交叉索塔顶处水平位移为
| $\partial {{a}_{{{r}_{1}}}}=F\frac{l_{{{l}_{1}}}^{3}}{{{a}^{2}}_{{{r}_{1}}}E{{A}_{{{l}_{1}}}}}.$ | (16) |
以下再求解索的伸长引起的右侧塔顶位移.根据式(10),索水平投影长度对索长求偏分得
| $\frac{\partial {{a}_{{{r}_{1}}}}}{\partial {{l}_{{{r}_{1}}}}}=\frac{{{l}_{{{r}_{1}}}}}{\sqrt{l_{{{l}_{1}}}^{2}-{{h}^{2}}}}=\frac{{{l}_{{{r}_{1}}}}}{{{a}_{{{r}_{1}}}}}.$ | (17) |
式(17)可得右侧塔顶位移∂ar1与拉索伸长∂lr1关系为
| $\frac{\partial {{a}_{{{r}_{1}}}}}{\partial {{l}_{{{r}_{1}}}}}=\frac{{{l}_{{{r}_{1}}}}}{{{a}_{{{r}_{1}}}}}.$ | (18) |
由塔顶水平力F引起的拉索r1的索力增量为
| $\partial {{T}_{{{r}_{1}}}}=F\frac{{{l}_{{{r}_{1}}}}}{{{a}_{{{r}_{1}}}}}.$ | (19) |
索力增大引起的r1的伸长量为
| $\partial {{l}_{{{r}_{1}}}}=\frac{\partial {{T}_{{{r}_{1}}}}{{l}_{{{r}_{1}}}}}{E{{A}_{{{r}_{1}}}}}=\frac{Fl_{{{r}_{1}}}^{2}}{E{{A}_{{{r}_{1}}}}{{a}_{{{r}_{1}}}}}.$ | (20) |
式(20)代入式(18),可得索的伸长引起塔顶的水平位移为
| $\partial {{a}_{{{r}_{1}}}}=\frac{Fl_{{{l}_{1}}}^{3}}{E{{A}_{{{r}_{1}}}}a_{{{r}_{1}}}^{2}}.$ | (21) |
由式(16)、(21)可得由主梁提升与索的伸长引起总的塔顶位移为
| $\partial {{a}_{{{r}_{1}}}}=\frac{Fl_{{{l}_{1}}}^{3}}{a_{{{r}_{1}}}^{2}E{{A}_{{{l}_{1}}}}}+\frac{Fl_{{{l}_{1}}}^{3}}{a_{{{r}_{1}}}^{2}E{{A}_{{{r}_{1}}}}}=\frac{F}{Ea_{{{r}_{1}}}^{2}}\left( \frac{l_{{{l}_{1}}}^{3}}{{{A}_{{{l}_{1}}}}}+\frac{l_{{{l}_{1}}}^{3}}{{{A}_{{{r}_{1}}}}} \right).$ | (22) |
由式(22)可得图 6中两根交叉索产生的对桥塔的纵向约束为
| ${{K}_{1}}=\frac{F}{\partial {{a}_{{{r}_{1}}}}}=\frac{Ea_{{{r}_{1}}}^{2}}{l_{{{l}_{1}}}^{3}/{{A}_{{{l}_{1}}}}+l_{{{l}_{1}}}^{3}/{{A}_{{{r}_{1}}}}}.$ | (23) |
假定跨中处梁段共有n对交叉索分别与两侧桥塔相连,则交叉索对桥塔总的约束刚度为
| $K=\sum\limits_{i=1}^{n}{{{K}_{i}}}.$ | (24) |
即
| $K=\sum\limits_{i=1}^{n}{\frac{Ea_{{{r}_{i}}}^{2}}{l_{{{l}_{i}}}^{3}/{{A}_{{{l}_{i}}}}+l_{{{l}_{i}}}^{3}/{{A}_{{{r}_{i}}}}}}.$ | (25) |
式(25)即一个主跨的交叉索对桥塔的纵桥向约束刚度表达式,由式(25)可以看出,交叉索的约束刚度主要与以下4个因素相关: 交叉索的长度、水平投影长度、弹性模量以及交叉索的面积. 实际上索的面积与弹性模量确定了索的轴向刚度,因此影响交叉索约束刚度的因素仅为索的长度、水平投影长度以及索的轴向刚度.
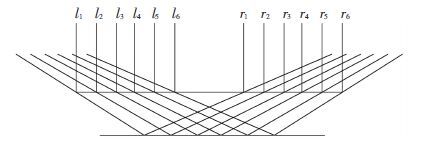
2 数值模拟验证为了验证公式的精确性,建立三塔四跨斜拉桥有限元模型,跨中采用交叉索提高结构刚度,比较有限元计算结果与本文公式计算值之间的差异. 桥跨布置为300 m +600 m +600 m+300 m,如图 7所示,桥塔材料为C50混凝土,主梁为Q345钢箱梁,桥塔高度为250 m,其中桥面以上150 m,桥面以下100 m. 主梁抗弯惯性矩为5.7 m4 ,桥塔抗弯惯性矩为400 m4 ,单位桥长重量为251.2 kN·m-1,一般拉索的横截面积为0.008 m2,边跨锚索横截面积为0.032 m2,C50混凝土弹性模量为34.5 GPa,钢箱、拉索弹性模量为200 GPa. 两个主跨均设置交叉索,每个主跨每个索面各有6对交叉索,交叉索的立面布置如图 8所示,交叉索纵向刚度计算见表 1.

|
图 7 三塔四跨斜拉桥立面布置 (m) Figure 7 Side view of cable-stayed bridge with three towers and four spans(m) |
|
图 8 交叉索编号 Figure 8 Number of the crossed cables |
| 表 1 交叉索纵向约束刚度 Table 1 Longitudinal restraint stiffness of the crossed cables |
根据表 1的计算结果,一个主跨的交叉索纵向约束刚度为
| $K=2\times \sum\limits_{i=1}^{6}{{{K}_{i}}}=22\text{ }708.76~kN/m.$ | (26) |
拉索在桥面两侧各有一个索面,因此式中乘2. 此刚度即中塔所受的一侧主跨交叉索的纵向约束刚度. 用有限元模型对本文公式进行验证时,主梁及桥塔刚度都对结构的变形有影响,为消除桥塔与主梁抗弯刚度的影响,约束1号塔及3号塔的纵向位移,模型中不考虑2号塔的纵向刚度(塔底设置为铰接),主梁抗弯惯性矩取为0.1 m4. 在2号塔塔顶施加集中力,集中力从2 000 kN增大至20 000 kN,计算塔顶位移.
塔顶位移的理论值为
| $d=\frac{F}{2K}.$ | (27) |
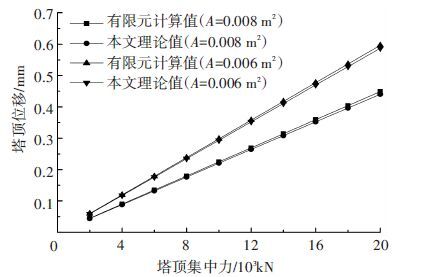
其中2号塔塔顶两侧都受到交叉索纵向约束作用,因此式(27)中需除以两倍纵向刚度. 本文理论值与有限元计算值绘于图 9中. 为保证验证的精确性,改变拉索的横截面积,令横截面积A=0.006 m2,其余参数保持不变,分别通过有限元及本文公式计算塔顶位移,同时绘于图 9中.
图 9可以看出,采用不同截面积的交叉索时,有限元计算结果与本文理论值均非常接近. 塔顶集中力增大至20 000 kN时,拉索截面采用0.008 m2时,塔顶位移的有限元计算值为0.449 m,本文理论值为0.440 m,相对误差约为2%;拉索截面采用0.006 m2时,塔顶位移的有限元计算值为0.597 m,本文理论值为0.587 m,相对误差约为1.7% 由此可以说明式(25)用于估算交叉索的纵向约束刚度具有较高精度.
|
图 9 塔顶施加水平集中力时的塔顶位移 Figure 9 Displacement of tower-top caused by horizontal concentrated force |
由上述研究可知,采用交叉索能够增大对桥塔的纵向约束作用,减小活载作用下桥塔的纵向位移. 为明确交叉索对多塔斜拉桥刚度的影响,对图 7三塔斜拉桥模型进行修改,并对第三跨施加均布荷载(如图 7所示),计算主梁变形,分析比较交叉索及桥塔、主梁对多塔斜拉桥刚度的影响.
模型A:采用原始模型,考虑交叉索及桥塔刚度. 模型B:在原模型基础上,不考虑桥塔抗推刚度(塔底设为铰接,桥塔仅提供竖向刚度). 模型C:去掉交叉索(去掉图 8中l4、l5、l6、r1、r2、r3).
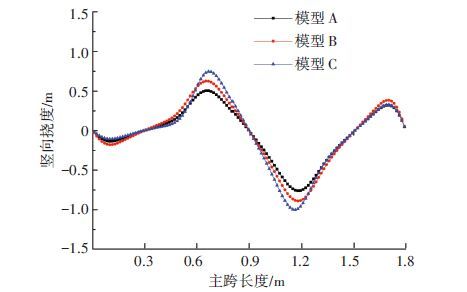
对模型A、B、C第三跨施加均布荷载集度40 kN/m,主梁的竖向挠度如图 10所示.
|
图 10 主梁竖向变形 Figure 10 Vertical deformation of the girder |
由图 10可以看出,采用交叉索的斜拉桥(模型A)比未采用交叉索的斜拉桥(模型C)跨中挠度降低约25%. 采用交叉索而无桥塔抗推刚度的斜拉桥(模型B)比未采用交叉索的斜拉桥(模型C)跨中挠度也有所减小. 由此说明交叉索对结构刚度的影响可以达到甚至超过桥塔刚度的影响.
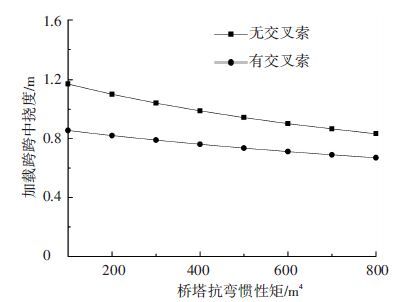
为考察桥塔刚度的影响,改变桥塔抗弯惯性矩,桥塔抗弯惯性矩从100 m4增大至800 m4,保持其他参数不变,加载跨跨中挠度变化如图 11所示.
在无交叉索的情况下,桥塔抗弯惯性矩从100 m4增大至800 m4时,跨中挠度下降了约30%. 若不增大桥塔刚度,而采用交叉索,跨中挠度明显减小,且减小幅度与增大桥塔刚度的效果类似. 由此可见,增大桥塔抗弯刚度与采用跨中交叉索均能有效增大结构刚度.
|
图 11 加载跨挠度与桥塔抗弯惯性矩之间关系 Figure 11 Relationship between deflection of the loaded span and bending inertia of the tower |
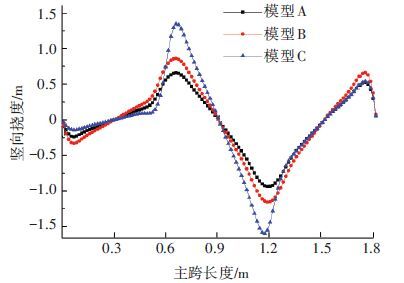
除桥塔刚度之外,主梁的抗弯刚度对结构总体刚度同样具有重要影响,同时,主梁的抗弯刚度对交叉索的约束效果也会产生影响. 为了研究主梁刚度的影响,将主梁抗弯惯性矩折减为原来的1/10,其余参数不变,第三跨施加均布活载后主梁变形如图 12所示.
|
图 12 主梁抗弯刚度折减后竖向变形 Figure 12 Vertical deformation after reduction of bending inertia of the girder |
图 12可以看出,主梁刚度减小后,模型A、B、C的主梁挠度均明显增大. 模型C的变形增大约60%,而模型A、B的最大挠度增大约20%~30%. 这说明主梁的抗弯刚度对结构总体刚度有明显影响,但采用交叉索后,主梁刚度对总体刚度的影响有所减小.
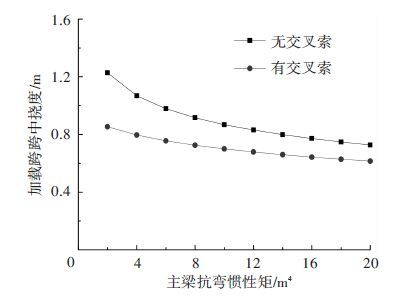
若保持模型A、C中桥塔刚度不变,改变主梁抗弯惯性矩,比较有无交叉索两种情况下的主梁挠度,如图 13所示.
|
图 13 加载跨挠度与主梁抗弯惯性矩之间关系 Figure 13 Relationship between deflection of the loaded span and bending inertia of the girder |
图 13可以看出,在主梁抗弯刚度较小时,有交叉索的斜拉桥主梁挠度比无交叉索时明显减小. 随着主梁抗弯刚度的增大,无交叉索的主梁挠度迅速减小,而有交叉索的主梁挠度减小幅度不大,有交叉索与无交叉索的主梁挠度逐渐接近. 这说明了在主梁刚度较小时,交叉索对于提高结构刚度具有明显效果,而随着主梁刚度的增大,交叉索的影响逐渐减小.
由图 11、13可以看出,增大桥塔刚度或主梁刚度均能使主梁挠度减小,但在未采用交叉索时,增大桥塔或主梁刚度对结构变形的效果更加明显. 在采用了交叉索之后,增大桥塔或主梁的刚度对减小挠度的效果有所降低. 说明在增加了交叉索之后,桥塔与主梁对结构整体刚度的影响有所减小,这也说明交叉索对结构刚度具有重要影响.
4 结 论1) 采用跨中交叉索的多塔斜拉桥在桥塔发生位移时,恒载在交叉索之间重新分配,据此推导了交叉索对桥塔约束刚度的解析公式. 研究表明,交叉索对桥塔的约束刚度与索的长度、水平投影长度以及索的轴向刚度有关.
2) 建立有限元模型对交叉索的纵向约束刚度解析公式进行了验证,结果表明,公式理论值与有限元计算值符合较好,公式可用于多塔斜拉桥的初步设计,指导交叉索参数的合理取值.
3) 研究了交叉索、桥塔刚度、主梁刚度对提高多塔斜拉桥刚度的影响,发现采用跨中交叉索、增大桥塔或主梁的抗弯刚度均能增大结构刚度,交叉索对结构刚度的影响甚至超过桥塔刚度对结构刚度的影响.
4) 在桥塔刚度或主梁刚度相对较低时,采用跨中交叉索可以显著增大结构刚度. 在桥塔及主梁抗弯刚度较大时,采用跨中交叉索对提高结构刚度的作用有所下降.
| [1] |
SAEKI S,FUJINO Y ,TADA K, et al.Technology aspects of the akashi kaikyo bridge[C]//Proceedings of ASCE Congress XIII. Boston: ASCE, 1995.
( 0) 0)
|
| [2] |
VIRLOGEUX M. Bridges with multiple cable-stayed spans[J].
Structural Engineering International,2001, 11 (1) : 61-82.
DOI: 10.2749/101686601780324250 ( 0) 0)
|
| [3] |
金立新, 郭慧乾. 多塔斜拉桥发展综述[J].
公路,2010 (7) : 24-29.
JIN Lixin, GUO Huiqian. Review on the development of multi-tower cable-stayed bridge[J]. Highway,2010 (7) : 24-29. (  0) 0)
|
| [4] |
喻梅, 李乔, 廖海黎. 辅助墩对多塔斜拉桥力学行为的影响[J].
世界桥梁,2010 (3) : 36-39.
YU Mei, LI Qiao, LIAO Haili. Effect of subsidiary piers on mechanical behavior of multi-pylon cable-stayed bridges[J]. World Bridges,2010 (3) : 36-39. (  0) 0)
|
| [5] |
喻梅, 李乔. 结构布置对多塔斜拉桥力学行为的影响[J].
桥梁建设,2004 (2) : 1-4.
YU Mei, LI Qiao. Effect of structural arrangement on mechanicalbehavior of multispan cable-stayed bridges[J]. Bridge Construction,2004 (2) : 1-4. (  0) 0)
|
| [6] |
曹珊珊, 雷俊卿, 李忠三, 等. 多塔斜拉桥刚度分析[J].
世界桥梁,2012, 40 (1) : 55-59.
CAO Shanshan, LEI Junqing, LI Zhongsan, et al. Analysis of rigidity of multi-pylon cable-stayed bridge[J]. World Bridges,2012, 40 (1) : 55-59. (  0) 0)
|
| [7] |
OKAMOTO Y, NAKAMURA S. Static and seismic studies on steel/concrete hybrid towers for multi-span cable-stayed bridges[J].
Journal of Constructional Steel Research,2011, 67 (2) : 203-210.
DOI: 10.1016/j.jcsr.2010.08.008 ( 0) 0)
|
| [8] |
COMBAULT J, TEYSSANDIER J P. Rion-Antirion Bridge, Greece-concept, design and construction[J].
Structural Engineering International,2005, 15 (1) : 22-26.
DOI: 10.2749/101686605777963387 ( 0) 0)
|
| [9] |
张喜刚, 王仁贵, 林道锦, 等. 嘉绍大桥多塔斜拉桥创新结构体系设计[J].
公路,2013, 7 : 286-289.
ZHANG Xigang, WANG Rengui, LIN Jindao, et al. Design of a multi-tower cable-stayed bridge with innovative structural system[J]. Highway,2013, 7 : 286-289. (  0) 0)
|
| [10] |
KITE S, CARTER M, HUSSAIN N. Design of the forth replacement crossing, scotland,UK[C]//IABSE Symposium Report, IABSE Symposium: Venice: IABSE, 2010.
( 0) 0)
|
| [11] |
GIMSING N J, GEORGAKIS C T.
Cable supported bridges concept and design[M]. New York: John Wiley & Sons, Ltd, 2011 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


