2. 同济大学 土木工程学院,上海 200092
2. 2.School of Civil Engineering, Tongji University, Shanghai 200092, China
弹性地基板分析属于两相介质的相互作用问题,其在工程中有很多应用,如机场道面、公路刚性路面、建筑物基础、机械的底座、船坞底板以及各种试验台等[1-2],其中很多情况下板会受到动力作用. 对于机场跑道而言,飞机降落、跑道的不平整引发振动、迫降等都会对道面产生冲击作用,而且国内外常采用落锤式弯沉仪和表面波频谱分析等方法,对现有道路和新建道路的品质进行快速而有效地评价[3]. 因此,研究冲击荷载下弹性地基板的动力响应具有重要意义. 自上世纪初以来,国内外学者对弹性地基板动力响应开展了广泛的研究,但是主要集中在解析解方面[4-11],关于弹性地基板的试验研究开展较少,文献[12]在砂基层上浇筑独立的混凝土板,考虑不同的脱空程度,研究了板的频率响应特性;文献[13]对3块足尺板进行试验,得到了板中心、板边和板角加载时的动弯沉曲线;文献[14-15]对弹性地基上的地基梁板进行了系统的模态测试研究;文献[16]用脉冲锤击法进行了弹性地基上自由板的自由振动模态试验,得到了7阶位移模态和应变模态. 本文首先开展弹性地基板的动力响应试验,分析板在冲击荷载作用下的运动过程,研究不同位置加载时板上特征点的响应规律. 接着,探讨功的互等定理在弹性地基板问题中的适用性,并据此得到板的弯沉盆形状. 最后,开展相关数值模拟,且与试验结果进行验证与分析.
1 试验模型制备试验采用上海市虹桥商务区核心区1号地块基坑开挖的②_1层土. 对取回土样先晒干、粉碎,然后根据干土含水率3%和最优含水率20%确定配水量. 由于配置的是非饱和土,采用洒水壶喷雾湿润表土,经多次翻拌和湿润,尽量保证均匀. 为了消除反射波的影响,在模型箱的侧壁放置2 cm厚的泡沫板,然后在泡沫板上划好分层界线,按照每层10 cm进行填土压实,通过含水量和密度来控制填土质量.
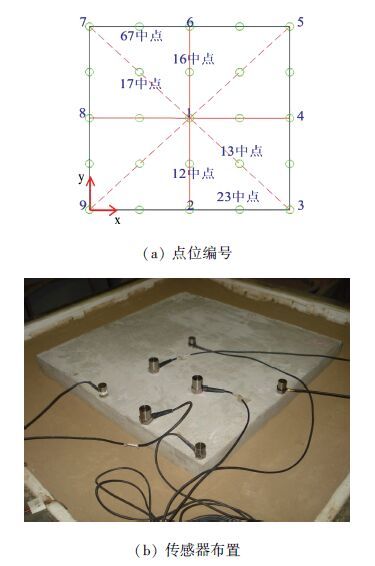
考虑常规机场跑道面板尺寸为5 m×5 m×0.4 m,根据几何相似,确定模型试验板尺寸为原型的十分之一(0.5 m×0.5 m×0.04 m),采用长宽高分别为0.9、0.9、0.8 m,壁厚2 cm的模型箱. 试验采用P.Ⅱ42.5水泥,水灰比0.4,砂灰比为1.0,不添加粗骨料,室温养护28 d. 如果在填筑好的地基上现浇混凝土板,则在养护过程中,地基水分会发生较大变化,故采用预制板进行试验. 试验前先用钢尺将地基刮平,然后将板放在地基表面中部,由于板底面和地基顶面都不是绝对的平整光滑,故存在局部接触不良情况. 后期试验表明,即便是现浇板,也无法消除边角处的脱空. 现浇板养护过程中,由于混凝土的干缩,边、角处会与地基发生脱离. 板越薄,其自重和抗弯刚度越小,对干缩变形的抵抗更弱,从而由干缩引起的细微脱空更严重. 试验前用锉刀打磨混凝土板,去掉表面浮灰,在板上标出特征点位置,如图 1(a)所示,然后黏贴加速度计,如图 1(b)所示,加速度计连接电荷放大器,经两次积分得位移. 飞机降落时,起落架冲击作用时间为0.01~0.4 s[13],落锤弯沉试验(FWD)荷载作用时间为0.02~0.03 s,而且荷载接近半正弦形状. 经过比较,选取具有橡胶头的力锤作为加载装置,其敲击混凝土板得到的冲击荷载持续时间接近0.01 s,并且为半正弦形状,见图 2(a). 飞机降落时,轮胎作用点可能在板上任意位置,而且用落锤弯沉仪进行道路检测时,也会选取板角、板中和板边等特征位置加载. 为此,将采用力锤依次在混凝土面板上各个特征点(共25个)施加冲击荷载,测量板的竖向位移响应.
|
图 1 传感器布置及特征点编号示意 Figure 1 Arrangement of sensors and sketch of numbered feature points |
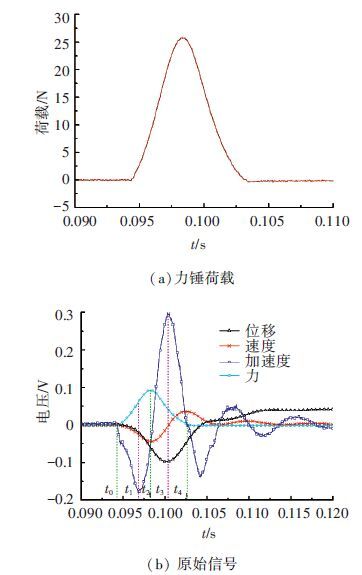
为了研究冲击荷载下混凝土板的运动规律,在试验的混凝土板上一点紧密布置3个传感器,分别设置为加速度、速度和位移输出. 用力锤敲击该点,得到原始响应数据,如图 2(b)所示,可以看出力锤时程曲线为半正弦形状,加速度时程曲线呈现出两个负峰值和一个正峰值,速度时程曲线呈现一个负峰值和一个正峰值,而位移曲线只有一个负的峰值.
当用力锤加载时,力锤在敲击点施加的向下荷载F1逐渐增大,图 2(b)中t0表示力锤与板接触时刻,敲击点向下运动的加速度逐渐增大,向下速度和位移也逐渐增大. 由于板向下运动时会受到地基土的限制,故地基土被压缩,并对板产生一个向上的反力F2. 在t1时刻,敲击点向下的加速度达到最大值. t0~t1时,F1的增速大于F2,从而向下的加速度一直增大,速度和位移也一直在增长. 在t1时刻之后,敲击点再向下运动,地基压缩量继续增大,地基反力的增速大于力锤荷载的增速,故而向下的加速度逐渐减小. 但此时F1的绝对值还是大于F2的绝对值,故敲击点加速度方向依然向下. 在t2时刻力锤荷载达到最大值,此时F2= -F1,加速度为0,向下速度达到最大值. t2时刻之后敲击点继续向下运动,F1减小,F2继续增大,由于此时地基反力的绝对值大于力锤荷载,故加速度为向上的正值. 在t3时刻向下位移达到最大值,向下的速度为0,此时向上的加速度达到最大值. 在t3时刻后,板开始回弹,敲击点速度方向转为向上正值,竖向位移逐渐减小. 由于地基土变形的恢复,地基反力F2减小(虽然此时力锤荷载F1也在减小,但是F2减小的幅度大于F1减小的幅度,F2的绝对值大于F1),向上运动的加速度逐渐减小. 在t4时刻,向上的加速度减小0,向上运动的速度达最大值,力锤荷载F1减小到0(由于加速度计具有一定尺寸,严格地讲,3个传感器不在同一位置,而且与力锤敲击点也不重合,故图 2(b)时程曲线存在一定误差).
|
图 2 力锤荷载与敲击点附近的加速度、速度与位移 Figure 2 Hammer loading and acceleration,velocity and displacement curves near hitting position |
之后,混凝土板继续向上运动而脱离地基,向下的加速度由重力产生. t0~t4时,板在力锤作用下作受迫振动,t4时刻后是完全的自由振动. 由于板的最大响应出现在力锤作用时间内,故下文将主要研究此时间段的响应.
2.2 面板动力响应分析在板的四分之一角集中布置传感器(点1、中点12、点2、中点23、点3、中点13和点4),然后在不同点施加冲击荷载,采集位移响应. 在手工敲击力锤时,施加荷载大小具有一定随机性,不便于对比分析. 为此,试验之前设定预期敲击荷载(26 N,对应1 V电压信号,此时地基处于弹性变形范围),然后控制实际敲击荷载与预期荷载误差不超过5%(对于不合标准的工况,采取多次重敲,直到达标为止). 最后将位移除以实际的荷载幅值并乘以26,即得到同样荷载(26 N)下不同位置加载时板的位移响应.
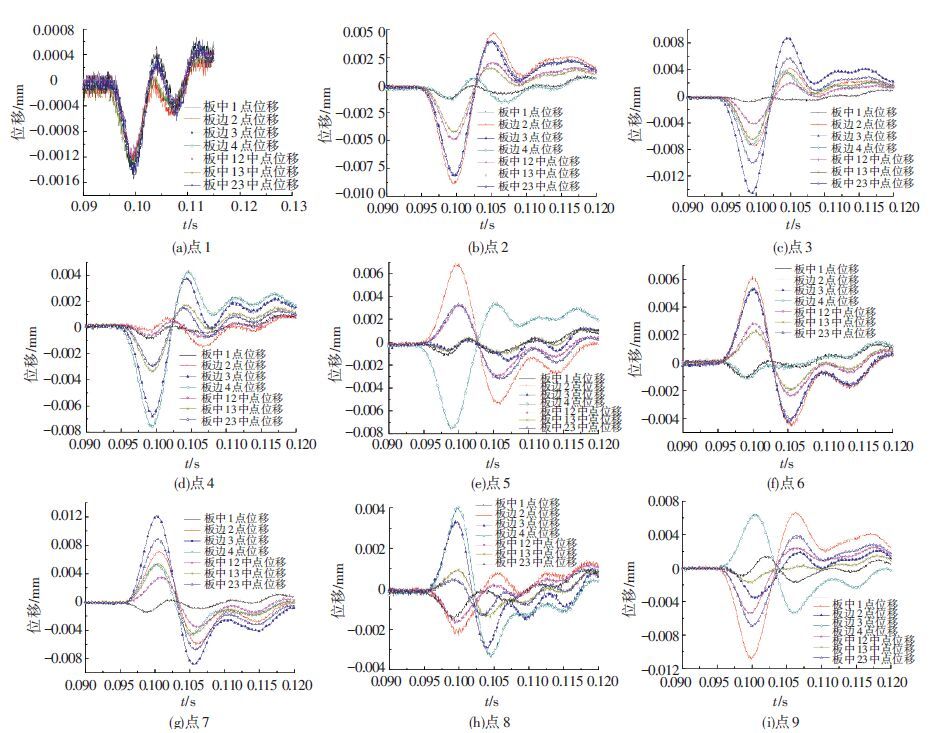
图 3是在板上不同位置加载时,7个传感器测得的竖向位移响应. 可见在板角点3加载时,竖向位移峰值最大. 当冲击荷载作用于板中心点1时,板整体下沉,地基反力分布较为均匀,竖向位移峰值最小,约为板角敲击时峰值位移的1/10. 而且此时荷载作用点靠近板的重心,位移曲线反向峰值较小. 在板边中部点2加载时,点2位移峰值最大,板角点3位移峰值次之(用Uy-x表示敲击点x时点y的位移响应),中点12位移峰值大致为点1和点2位移峰值的平均值,即U12-2≈ (U1-2+U2-2)/2. 点3加载时,由于点2和点4相对于点3位置对等,故有U2-3=U4-3,其峰值略大于U13-3的峰值. 在板中心、板边、板角加载时,位移曲线形状与文献[13]得到的很相似.
在点1、2、3和点4加载时,所有传感器都位于弯沉盆内部,故竖向位移首个峰值为负. 理想情况下,U2-2=U4-4,实际上由于板与地基局部接触不均匀,U2-2与U4-4相比存在一定的差别. U2-9>U2-2,表明点9附近存在一定程度脱空. 点5加载时,点2、中点12与中点23都处在弯沉盆之外,故其位移曲线首个峰值为正,但此时点1、中点13和点3位移为较小的负值,表明其在弯沉盆内部靠近弯沉盆边缘位置. 点6加载时,U2-6的峰值是此时板上所有正向位移中最大的. 同样,U3-7和U4-8也分别是点7和点8加载时,板上正向位移最大者. 这是因为26连线,37连线以及48连线都是板的对称轴,故可知敲击板对称轴一端时,其另外一端点的正向位移最大. 在点6、7和8加载时,中点13处位移为正,表明其在弯沉盆之外;同样,在点5、6和7处加载时,中点12也处在弯沉盆之外. 点7处加载时,除了板中心的点1,其余传感器都在弯沉盆之外. 在点8和9加载时,点2处位移峰值偏大,这与点9附近的脱空有关.
2.3 功的互等定理应用对于线弹性系统,存在功的互等,即第1状态外力在第2状态位移上所作的功W12,等于第2状态外力在第1状态位移上所作的功W21,即FP1δ12= FP2δ21. 其中FP1为第1状态时点1作用荷载,δ21为其在点2处产生的位移,FP2为第2状态时点2作用荷载,δ12为其在1点处产生的位移.
|
图 3 不同位置加载时板的响应 Figure 3 Responses of slab when loading at different positions |
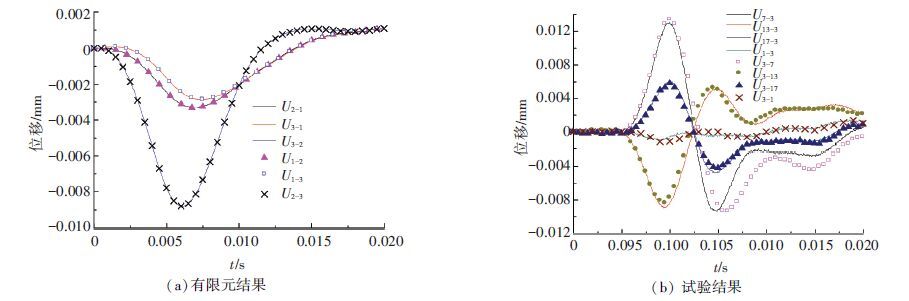
为了验证互等定理在弹性地基板中的适用性,分别采用有限元商业软件(ABAQUS)计算和试验测试结果进行对比. 在有限元计算时,模型尺寸按照试验模型建立,混凝土和土都采用线弹性本构,其界面采用库伦摩擦接触. 混凝土的密度2 280 kg/m3,弹性模量29 GPa,泊松比0.15;地基土密度1 812 kg/m3,弹性模量30 MPa,泊松比0.35,采用试验测得的力锤荷载. 图 4(a)为有限元计算结果,可以看出点1加载时点2位移(记作U2-1),与点2加载时点1位移(记作U1-2)完全重合,其他点也具有同样的规律. 表明在理想接触条件下(两个接触面都光滑平整),冲击荷载不变时,存在位移互等现象,即敲击点x引起点y的位移Uy-x与敲击点y时引起点x的位移曲线Ux-y完全重合. 在试验中,由于板和地基不是光滑平行平面,板边、角处与地基并非完全接触,再加上地基土非线性特征,故互等现象与理论会有一定偏离. 图 4(b)为实测点3加载时,点7、中点13、中点17及点1处位移响应,与分别在这4个点加载时,点3处位移响应的对比图. 可看出U17-3和U3-17误差略大,其他点互等现象很明显.
|
图 4 位移互等分析 Figure 4 Analysis of reciprocal displacement |
在板边中部点2黏贴传感器,依次敲击板上25个特征点,可得不同位置加载时点2位移响应曲线 (U2-x). 根据位移互等定理(U2-x =Ux-2),从而可得点2敲击时,板的弯沉盆形状. 用同样方法得到点6、3和7处加载时板的弯沉盆,如图 5所示.
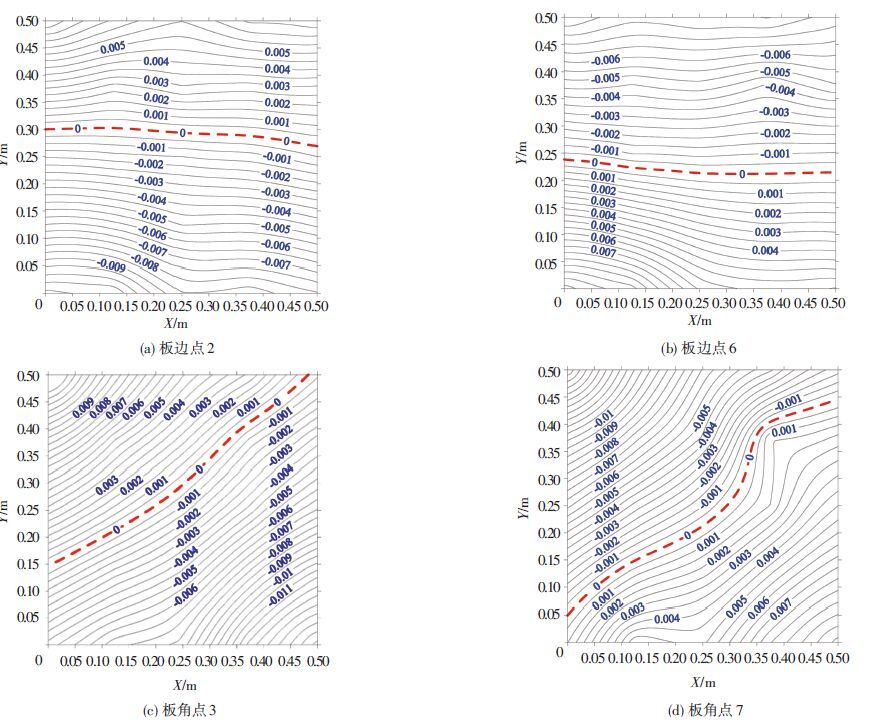
在点2(X=0.25 m,Y=0 m) 加载时,点9(X=0 m,Y=0 m)和点2处于板同侧,首个位移峰值为负. 对于理想接触情况,U2-2的幅值大于U9-2,但由于点9处存在脱空,导致U9-2幅值偏大. 即板边中部点2加载时,板角点9位移幅值最大. 脱空处位移等值线密度增加,形状发生改变,曲率显著增大. 弯沉盆界线(即竖向位移为0的等值线)在Y=0.25~0.31 m之间,略微超过板的对称轴. 点6(X=0.25 m,Y=0.5 m) 加载时,此时3-9边与地基脱离,首个位移峰值为正(点6加载时理论最大正向位移发生在点2),但从图 5(b)可看出,U9-6的幅值明显大于U2-6(更大于U3-6). 因此脱空区无论是在弯沉盆内还是在弯沉盆外,其位移响应幅值都比同等位置非脱空处要大. 图 5(c)、5(d)是敲击板角点3和点7时板的弯沉盆,板角敲击时弯沉盆界线在对角线附近,最大向下位移发生在敲击板角,最大向上位移发生在敲击点所在对角线另一端. 竖向位移由敲击点向远处成辐射状分布,在弯沉盆界线处,位移等值线的曲率最小. 板角敲击时,其位移等值线图难以反映出点9处的脱空情况.
|
图 5 不同点加载时板的弯沉盆(mm) Figure 5 Deflection basin when loading at different positions(mm) |
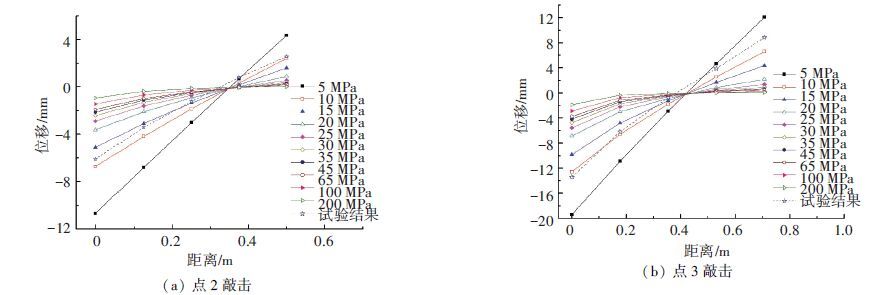
采用数值分析结果拟合试验结果的方法,可以确定模型地基弹性模量. 由于试验时板与地基接触状态对竖向位移绝对值影响非常大,此处采用能反映板上各点相对弯沉的特征曲线形状作为拟合指标. 对于板边点2加载工况,选取点2与点6连线(板中线)作为特征曲线;对板角点3加载工况,选取点3与点7连线(对角线)为特征曲线,每条特征曲线上有5个特征点. 采用有限元软件ABAQUS,对不同弹性模量的地基模型进行计算,提取每个工况中5个特征点处的竖向位移峰值. 以特征点到加载点距离为横坐标,特征点竖向位移峰值为纵坐标,得到不同地基弹性模量时特征曲线形状,如图 6所示. 弹性模量不同时,特征曲线斜率不一样. 在弹性模量较小时,敲击点负向位移峰值和翘起点正向位移峰值都比较大,从而特征曲线的斜率较大,并且地基弹性模量较小时特征曲线更接近直线,由此可根据特征曲线形状结合有限元计算反求地基弹性模量. 板边点2加载时,试验结果在10~15 MPa的有限元结果之间,如图 6(a)所示. 板角点3加载时,试验结果与15 MPa的有限元结果有一定偏离,如图 6(b)所示.
|
图 6 不同地基弹性模量时特征曲线 Figure 6 Characteristic curve of different foundation modulus |
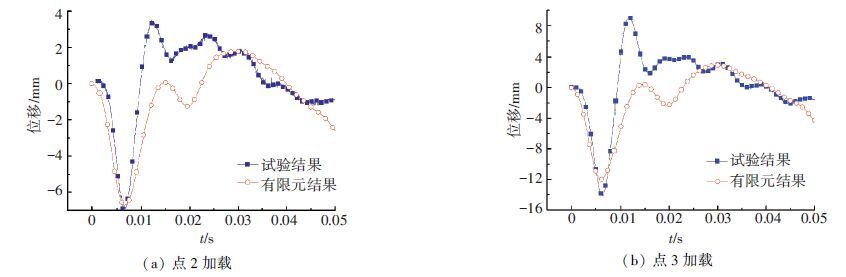
图 7为板边点2和板角点3加载时,试验和数值模拟(地基弹性模量10 MPa)得到的敲击点位移时程曲线. 可以看出曲线下降段形状比较相似,而上升段差别较大,试验曲线在0.01 s之后出现较大的向上位移,这是因为试验中板底面和地基顶面都不是绝对平整光滑,界面接触不均,当荷载作用点偏离重心时,会产生摇晃,加载结束后出现向上的位移. 而在有限元建模时,板底面和地基顶面都是绝对光滑平整的,在加载之前接触良好,不会产生摇晃. 导致试验和有限元结果不一致的因素包括: 有限元计算时的边界、板与地基界面接触、混凝土和土的本构以及加载方式等与试验情况均有一定差别.
|
图 7 试验与数值结果对比 Figure 7 Comparison of experimental and numerical results |
图 8(a)、8(b)为分别给出板边点2和板角点3加载时,道面板竖向位移峰值最大时刻云图. 对比图 5中的弯沉盆,可以看出试验得到的弯沉盆形状与有限元计算出的弯沉盆形状很相似.

|
图 8 竖向位移云图(m) Figure 8 Contours of vertical displacement(m) |
1) 依据冲击点加速度、速度和位移时程曲线形状分析,可揭示冲击点受力和运动的过程. 冲击点在力锤荷载和地基反力综合作用下,先加速再减速向下运动,在位移最大处,速度为零,向上运动加速度达最大值,之后减速向上运动,在外载移去后板做自由振动.
2) 板角敲击时加载点竖向位移峰值最大,板中心加载时竖向位移峰值最小. 在不脱空情况下,板边中部敲击时加载点向下位移最大,而该敲击点所在对称轴另一端向上的位移最大,对于板角敲击也具有同样规律. 板角脱空时,敲击板边中点,板角向下位移可能比敲击点的大.
3) 当功的互等定理满足时,可用少量传感器结合多点加载,就能得到板在冲击荷载作用下的完整弯沉盆形状. 板边中点加载时弯沉盆界线在板中附近,板角加载时弯沉盆界线在对角线附近,且根据板边中点加载时的弯沉盆形状能有效地判别板角处的脱空状况.
4) 地基弹性模量不同导致特征曲线斜率存在差别,故可根据特征曲线形状结合有限元计算反求出地基的弹性模量. 由于试验中板边、板角处不可避免地存在接触不均,荷载较小时,试验与数值模拟得到板的位移值有一定误差,但在弯沉盆形状上具有较高相似性.
| [1] |
王克林, 黄义. 弹性地基上四边自由矩形板[J].
计算结构力学及其应用,1985, 2 (2) : 47-58.
WANG Kelin, HUANG Yi. Rectangular plates with four free edges on elastic foundations[J]. Computation Structural Mechanics and Applications,1985, 2 (2) : 47-58. (  0) 0)
|
| [2] |
王元汉, 邱先敏, 张佑启. 地基板的等参有限元法计算[J].
岩土工程学报,1998, 20 (4) : 7-11.
WANG Yuanhan, QIU Xianmin, ZHANG Youqi. Plates on an elastic foundation calculated by isoparametric element methods[J]. Chinese Journal of Geotechnical Engineering,1998, 20 (4) : 7-11. (  0) 0)
|
| [3] |
颜可珍, 夏唐代, 黄立葵. 双参数粘弹性地基无限长板的瞬态响应分析[J].
岩石力学与工程学报,2005, 24 (24) : 4576-4580.
YAN Kezhen, XIA Tangdai, HUANG Likui. Dynamic response of strip on two-parameter viscoelastic foundation under impact loading[J]. Chinese Journal of Rock Mechanics & Engineering,2005, 24 (24) : 4576-4580. (  0) 0)
|
| [4] |
LEISSA A W. The free vibration of rectangular plates[J].
Journal of Sound and Vibration,1973, 31 (3) : 257-293.
DOI: 10.1016/S0022-460X(73)80371-2 ( 0) 0)
|
| [5] |
SAVIDIS S A, RICHTER T. Dynamic response of elastic plates on the surface of the half space[J].
International Journal for Numerical Analytical Methods in Geomechanics,1979, 3 : 245-254.
DOI: 10.1002/(ISSN)1096-9853 ( 0) 0)
|
| [6] |
WHITTAKER W L, CHRISTIANO P. Dynamic response of plate on elastic half space[J].
Journal of Engineering Mechanics,1982, 108 : 133-154.
( 0) 0)
|
| [7] |
尹邦信. 弹性板受撞击的动力响应分析[J].
应用数学和力学,1996, 17 (7) : 639-644.
YIN Bangxin. Analysis of dynamic response of an impacted elastic plate[J]. Applied Mathematics and Mechanics,1996, 17 (7) : 639-644. (  0) 0)
|
| [8] |
张选兵, 罗先启, 葛修润, 等. 双参数弹性地基上板承受冲击荷载的动力响应的解析解[J].
岩石力学与工程学报,2001, 20 (6) : 846-850.
ZHANG Xuanbing, LUO Xianqi, GE Xiurun, et al. Analytical solution on dynamic response of rectangular plate with free edges on two parameters elastic foundation under impact load[J]. Chinese Journal of Rock Mechanics & Engineering,2001, 20 (6) : 846-850. (  0) 0)
|
| [9] |
祝彦知, 薛保亮, 王广国. 粘弹性地基上粘弹性地基板的自由振动解析[J].
岩石力学与工程学报,2002, 21 (1) : 112-118.
ZHU Yanzhi, XUE Baoliang, WANG Guangguo. Free vibration analysis of viscoelastic foundation plate on viscoelastic foundation[J]. Chinese Journal of Rock Mechanics & Engineering,2002, 21 (1) : 112-118. (  0) 0)
|
| [10] |
谢洪阳.弹性地基板动力问题的数值分析[D].武汉: 华中科技大学, 2006.
XIE Hongyang. Numerical analyses for dynamic problems of elastic foundation plates[D]. Wuhan: Huazhong University of Science & Technology, 2006. (  0) 0)
|
| [11] |
钟阳, 孙爱民, 刘文光. 弹性地基上四边自由矩形薄板的自由振动[J].
振动工程学报,2006, 19 (4) : 566-570.
ZHONG Yang, SUN Aimin, LIU Wenguang. Free vibration of rectangular thin plate on elastic foundation with four edges free[J]. Journal of Vibration Engineering,2006, 19 (4) : 566-570. (  0) 0)
|
| [12] |
MCCAVITT N, YATES M R, FORDE M C. Dynamic stiffness analysis of concrete pavement slabs[J].
Journal of Transportation Engineering,1992, 118 (4) : 540-556.
DOI: 10.1061/(ASCE)0733-947X(1992)118:4(540) ( 0) 0)
|
| [13] |
许金余, 邓子辰.
机场刚性道面动力分析[M]. 西安: 西北工业大学出版社, 2002 .
XU Jinyu, DENG Zichen. Dynamic analysis of rigid airport pavement[M]. Xi'an: Northwestern Polytechnical University Press, 2002 . (  0) 0)
|
| [14] |
曾亚. 混板静、动力特性及损伤诊断研究[D]. 长沙: 湖南大学, 1998.
ZENG Ya. Study on static and dynamic characteristic and damage diagnosis of rigid pavement[D]. Changsha: Hunan University, 1998. (  0) 0)
|
| [15] |
张望喜. 混凝土地基板静、动力特性试验与研究[D]. 长沙: 湖南大学, 2002.
ZHANG Wangxi. Test and research on static & dynamic characteristic of concrete slab[D]. Changsha: Hunan University, 2002. (  0) 0)
|
| [16] |
易伟建, 周云, 张望喜. 弹性地基板模态试验及地基动参数识别[J].
中国公路学报,2007, 20 (2) : 1-6.
YI Weijian, ZHOU Yun, ZHANG Wangxi. Modal experiment on elastic foundation slab and identification of dynamic foundation parameters[J]. China Journal of Highway and Transport,2007, 20 (2) : 1-6. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


