磁致伸缩现象是满足自由能极小条件的必然结果[1],从磁畴唯象理论来说主要是由外磁场的磁畴偏转和畴壁运动而引起的. GMM 因其具有能量转换效率高(机电耦合系数>0.7)、磁致伸缩应变量值大(饱和磁致伸缩应变>10-3)、居里温度高(380~800 ℃)、动态响应时间短(<1 μs)、频响特性好(0~500 Hz)、能量密度高(14~25 kJ/m3)[2-5]等优点,在主动减振、传感器、换能器、精密控制[6-9]等领域得到了广泛的应用. 由于GMM具有较强的抗压特性和较弱的抗拉特性,如果GMM棒处于不均匀的磁场中,一方面在对其进行测控时会出现高次谐波而导致谐频输出,另一方面由于各个磁畴之间的伸缩位移不同导致磁畴之间的拉压性不一致,应力分布不均匀,从而大大降低超磁致伸缩棒的力学性能,使材料特性受损,因此,磁场强度的均匀性是充分发挥GMM性能的关键因素. 磁路主要是为GMM棒提供驱动环境,因此磁路环境的好坏直接关系到GMA的工作性能. 文献[10-12]开展了对GMA磁路的研究,得到了良好的磁场环境,但是主要是从增加导磁体形成闭合磁路提高磁场利用率的角度进行的研究,没有开展闭合磁路中导磁体对于提高磁路的均匀性和磁场利用率的研究,也没有形成系统性的设计方法和理论依据[13-15]. 对于磁路的设计基本上是仅仅依赖于磁场的有限元分析[15-18],没有开展磁路中导磁体的关键结构参数对于提高磁路性能的影响规律的研究. 因此,在对磁路进行优化设计过程中提出以减小磁漏、增大磁场强度和提高磁场强度的均匀性为设计原则,基于ansoft maxwell和高斯磁通理论对磁路中关键导磁体的结构参数对磁场强度大小和均匀性的影响规律进行探索和理论研究,在此基础上对导磁体的结构参数进行优化设计,试验结果表明,GMM棒的磁场强度的均匀性和大小得到了很大程度的提高,对于提高GMA的工作性能具有一定的指导意义.
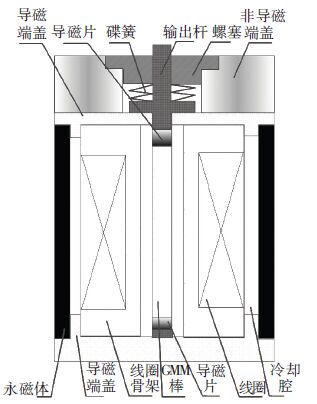
1 GMA工作原理超磁致伸缩作动器是利用GMM棒在外界激励磁场中产生对外输出位移来驱动其他装置动作,具有输出位移大、位置控制精度高、频响快等优点. 典型GMA的结构如图 1所示,永磁体提供偏置磁场消除倍频现象,螺塞与碟簧提供预压力,励磁线圈提供激励磁场. GMA采用环形外套式永磁体产生偏置磁场,一方面可以消除GMM自身的倍频特性实现双向位移输出,另一方面可以产生较大的偏置磁场、能耗低发热量小[19]. GMM的线性本构方程为
| $\varepsilon =\frac{\sigma }{{{E}^{H}}_{y}}+{{d}_{33}}H,$ | (1) |
| $B={{d}_{33}}\sigma +{{\mu }^{\sigma }}H.$ | (2) |
|
图 1 GMA的结构示意 Figure 1 Structural schematic diagram of GMA |
式中:ε为材料应变;σ为材料所受应力;d33为压磁系数;EyH为材料弹性模量;H为磁场强度;B为磁感应强度;μσ相对为磁导率.
由式(1)、(2)可知,如果GMM棒各处的磁场强度H不同,磁畴微元之间将会产生不同的应变ε,因此相邻微元之间因应变大小及方向不同而导致材料本身拉压特性不一致,严重破坏了材料的力学性能[20],因此必须提高GMM棒所处磁场强度的均匀性,良好的导磁回路不但可以在很大程度上改善其磁场的均匀性,同时还可以减小磁漏、提高磁场强度从而减小能量消耗. 由于GMM棒中轴线上从中点到两端磁场强度呈现单调递减趋势,因此为了评价GMM棒所处磁场的均匀性,本文提出以磁场均匀率作为衡量磁场均匀性的指标,其值接近于1越均匀,磁场均匀率表达式为
| $\eta =(1-\frac{{{H}_{max}}-{{H}_{min}}}{{{H}_{max}}})\times 100%.~$ | (3) |
式中Hmax为GMM棒轴线处的最大磁场强度;Hmin为GMM轴线处的最小磁场强度.
2 基于ansoft maxwell有限元分析由GMA的磁回路模型可知,GMA属于3D轴对称几何结构,因此可以将其简化为2D平面模型进行有限元分析计算. 本文利用ansoft maxwell 14.0作为有限元计算工具对GMA磁回路进行有限元分析,以GMM棒中轴线处的磁场强度大小和均匀性作为衡量磁回路优劣的标准.
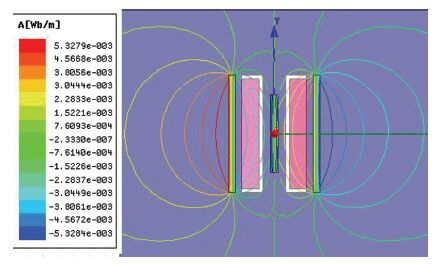
GMA磁回路在ansoft maxwell 14.0环境下建立有限元模型,对其进行自由网格划分,激励条件是当激励电流为5 A(最大励磁电流的一半)时电流密度为1.46 MA/m2,边界条件为balloon气球边界条件. 当无导磁端盖和导磁片时对磁回路进行电磁学有限元分析,其磁场分布及GMM棒沿轴向的磁场强度分布如图 2、3所示.
|
图 2 磁场分布 Figure 2 Magnetic field distribution |
|
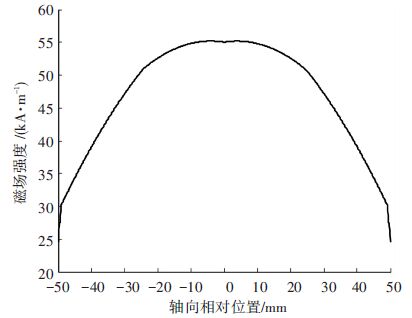
图 3 GMM棒轴向磁场强度 Figure 3 Axial magnetic field intensity of GMA rod |
由图 2、3可知,在磁路的两端和永磁体外侧存在很大的磁漏,最大磁场强度为55.4 kA/m,最小磁场强度为24.5 kA/m,磁场均匀率为44.22%. 为了减小端部磁漏,改善GMM棒处的磁场环境,加入导磁端盖和导磁片. 由高斯磁通定理可知,导磁端盖可减小端部磁漏,提高磁场的利用率,导磁片主要用来改善GMM棒处的局部磁路环境从而可以提高GMM棒磁场的均匀性.
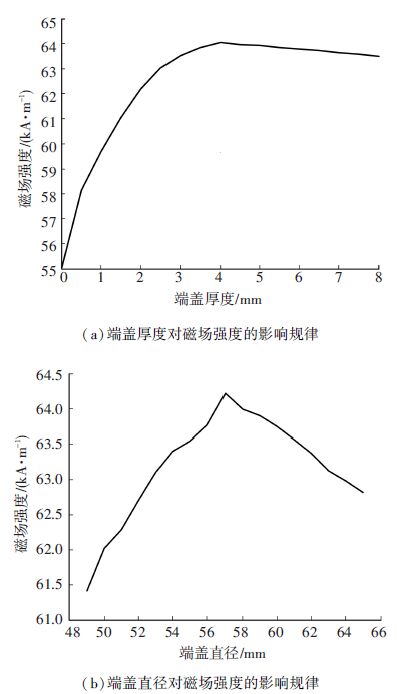
3 关键导磁体的优化设计 3.1 导磁端盖的优化设计由于磁场为无源场,根据磁通的连续性定理可知,穿入一闭合平面的磁通等于穿出的磁通. 为了改善GMM棒处的磁场环境减小漏磁,需要增加上下导磁盖来抑制端部漏磁. 由于GMM棒的磁导率相对较低(仅为空气磁导率的2~10倍),因此本文在磁路的两端设计了具有高结构强度和磁导率的导磁端盖,材料为20#钢. 导磁端盖的主要参数为厚度和直径,根据高斯磁通定理及结构形式可知厚度和直径对于抑制漏磁的影响依次减弱. 因此需要分别根据各自的影响变化趋势依次确定其结构参数. 以GMM棒轴线上最大磁场强度为目标变量,分别以导磁端盖的直径和厚度为因变量经过有限元分析可以得到其函数关系如图 4所示.
|
图 4 GMM棒轴向磁场强度 Figure 4 Axial magnetic field intensity of GMM rod |
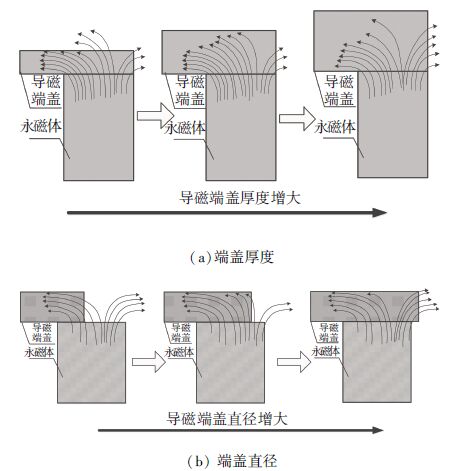
由图 4(a)可知,GMM棒的最大磁场强度随着导磁端盖厚度的增大而呈现先增大后减小的变化趋势. 这是由于随着导磁端盖厚度的增大,励磁线圈和永磁体端部漏磁减小,GMM棒处的磁通增大,当导磁端盖的厚度继续增大,厚度对端部磁漏的影响减小反而使外侧的磁漏增大,如图 5(a)所示. 因此导磁端盖应选择合适的厚度可以减小磁漏、增大磁场强度. 由图 4(a)可知,磁场强度最大时导磁端盖的厚度为4 mm.
|
图 5 端盖参数对GMM棒磁场强度的影响 Figure 5 Laws between cover parameters and magnetic field intensity |
由图 4(b)可知,当永磁体的内径为50 mm,外径为59 mm时,最大磁场强度随导磁端盖直径的增大而呈现先增大后减小的趋势. 这是由于随着直径的增大,永磁体外侧的磁漏减小,GMM棒的磁通增大,当直径继续增大,此时永磁体外侧的磁漏变大,如图 5(b)所示. 由图 4(b)可知,磁场强度最大时导磁端盖的外径为57 mm,而永磁体的内径为50 mm,外径为59 mm,中径为54.5 mm,因此可以得出一个结论:导磁端盖的直径在永磁体中径和外径之间.
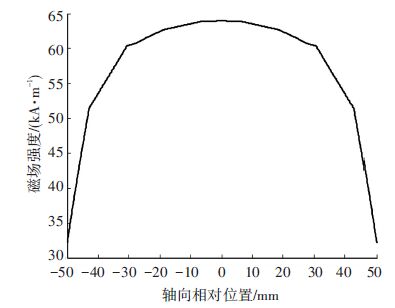
当导磁端盖厚度为4 mm,外圆直径为57 mm时,磁场分布及GMM轴线处的磁场强度如图 6所示. 从图 3和图 6对比可以看出最大磁场强由55.4 kA/m增大了63.99 kA/m,磁场强度增大了15.5%,磁场均匀率由44.22%增大到了50.4%,由此可知磁场强度显著增大,磁场的均匀性虽有所提高,但是不很明显.
|
图 6 GMM棒轴向磁场强度 Figure 6 Axial magnetic field intensity of GMM rod |
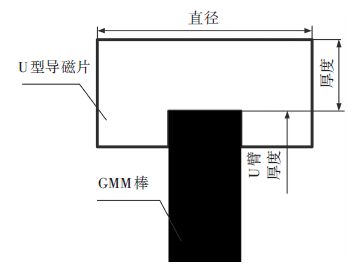
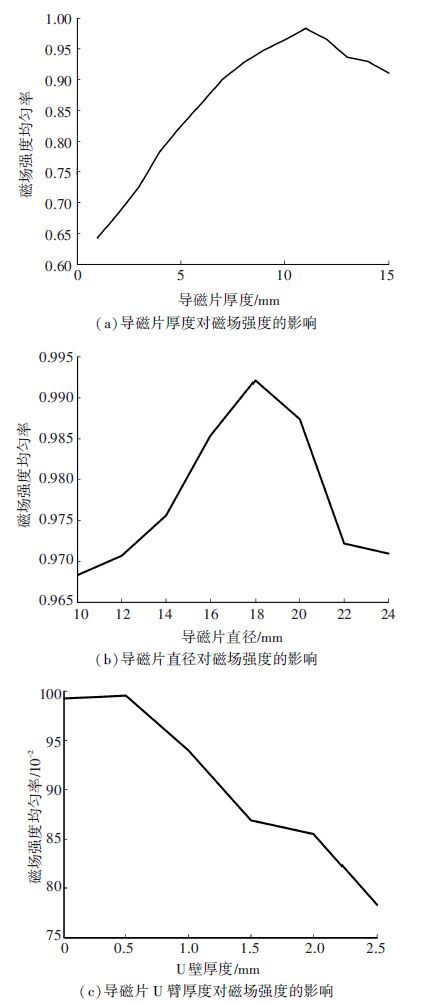
由图 6可知,由于端部效应的影响GMM棒端部磁场强度相对较低,磁场的均匀性很差. 为了改善磁回路中GMM棒磁场强度的分布,增大磁场强度的均匀性,本文首次提出在GMM棒的两端增加U型导磁片的方式来最大限度的提高磁场的均匀性. 导磁片材料选用结构强度和导磁率很高的20#钢,导磁片的主要尺寸参数为厚度、直径和U臂厚度,如图 7所示. 而厚度、直径和U臂厚度对磁场均匀性的影响程度依次减弱,因此需要分别根据各自的变化趋势依次确定其结构参数. 以GMM棒中轴线上的磁场强度均匀率为目标变量,分别以导磁片的厚度、直径和U臂厚度为因变量,经过有限元计算分析可以得到其函数关系,如图 8所示.
|
图 7 U型导磁片 Figure 7 U Magnetic sheet |
|
图 8 GMM棒磁场强度均匀率变化曲线 Figure 8 Uniformity of magnetic field intensity in GMM rod |
由图 8(a)可知,GMM棒中轴线上的磁场强度均匀率随着导磁片厚度的增大呈现先增大后减小的变化趋势. 这是由于导磁片的厚度越大,GMM棒端部附近的磁阻越小、磁场强度变大并逐渐的接近、超过中心磁场强度. 由图 8(a)可知,当导磁片的厚度为11 mm时磁场强度的均匀率最高.
由图 8(b)可知,GMM棒中轴线上的磁场强度均匀率随着导磁片直径的增大呈现先增大后减小的变化趋势. 这是由于随着导磁片直径的增大,GMM棒端部附近的磁阻越小、磁场强度增大并逐渐的接近、超过中心磁场强度. 由图 8(b)可知,当导磁片的直径为18 mm时磁场均匀率最高.
由图 8(c)可知,GMM棒中轴线上的磁场强度均匀率随着导磁片U臂厚度的增大呈现先增大后减小的变化趋势. 这是由于随着导磁片U臂厚度的增大,GMM棒端部效应减小,端部的磁场强度相对逐渐减小,因此磁场的均匀率呈现先增大后减小的趋势. 由上述优化分析可知,当导磁片的U臂厚度为0.5 mm时磁场均匀率最高.
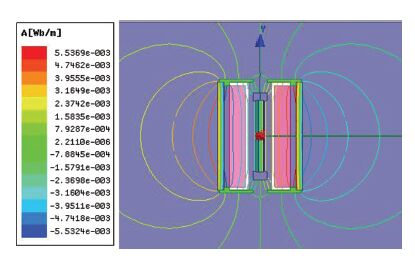
4 磁回路的实验研究根据导磁端盖和导磁片的结构参数对磁路环境的影响规律对其进行优化设计,当导磁端盖的直径为57 mm,厚度为4 mm,导磁片的直径为18 mm,厚度为11 mm,U臂厚度为0.5 mm时磁场分布如图 9所示,将其设计成磁致伸缩作动器,如图 10所示.
|
图 9 优化后磁场分布 Figure 9 Magnetic field distribution after optimization |

|
图 10 GMA试验台 Figure 10 GMA test bed |
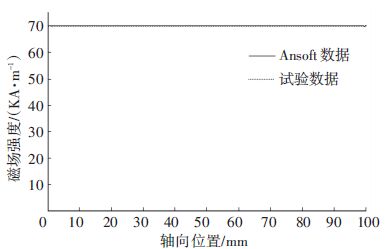
沿着GMM棒轴线方向安装磁场强度传感器,当输入激励电流为5 A时,利用RTX为下位机LabWindows为上位机采集传感器的数据信息,在GMM轴线方向不同点测量磁场强度与有限元分析如图 11所示. 由于测量数据为GMM棒外径轴线上的磁场强度,比有限元分析的中轴线数据稍微较小,但变化趋势基本相同. 从图 3和图 11对比可以看出最大磁场强由55.4 kA/m增大了70.35 kA/m,磁场强度增大了26.98%,磁场均匀率由44.22%变为99.5%,由此可知磁场强度显著增大,磁场均匀性得到明显改善.
|
图 11 GMM棒轴向磁场强度 Figure 11 Magnetic field intensity along GMM rod |
1) 导磁端盖主要用来减小磁漏、提高磁场强度,导磁片主要用来提高GMM棒处磁场强度的均匀性.
2) GMM棒处的磁场强度随着导磁端盖的厚度和直径的增大呈现先增大后减小的趋势,厚度和直径对提高磁场强度的影响依次减弱,因此需要根据各自的变化趋势依次确定其参数.
3) 导磁端盖的直径在永磁体中径与外径之间时可最大程度减小磁漏,提高磁场强度.
4) U型导磁片可以最大限度的改善磁路环境、提高磁场的均匀性,且磁场均匀性随着其厚度、直径和U臂厚度的增大呈现先增大后减小的趋势. U型导磁片的厚度、直径和U臂厚度对磁场均匀性的影响程度依次减弱,因此需要分别根据各自的变化趋势依次确定其结构参数.
| [1] |
SMITH R C, DAPINO M J, STEFAN S L. A free energy model for hysteresis in magnetostrictive transducers[J].
Journal of Applied Physics,2003, 93 (1) : 458-466.
DOI: 10.1063/1.1524312 ( 0) 0)
|
| [2] |
杨大智.
智能材料和智能系统[M]. 天津: 天津大学工业出版社, 2003 : 284 -296.
YANG Dazhi. Intelligent material and intelligent system[M]. Tianjin: Tianjin Industry University Press, 2003 : 284 -296. (  0) 0)
|
| [3] |
LIU Jinghua, JIANG Chengbao. Giant magnetostrictive materials[J].
Journal of Applied Physics,2015, 55 (5) : 1319-1326.
( 0) 0)
|
| [4] |
刘红军, 刘洁, 叶芳. 用于超磁致伸缩作动器的一种改进的控制方法[J].
哈尔滨工业大学学报,2012, 44 (9) : 91-95.
LIU Hongjun, LIU Jie, YE Fang. An improved control method for the giant magnetostrictive actuator[J]. Journal of Harbin Institution of Technology,2012, 44 (9) : 91-95. (  0) 0)
|
| [5] |
王博文.
超磁致伸缩材料的制备与器件设计[M]. 北京: 冶金工业出版社, 2003 : 132 -146.
WANG Bowen. Preparation and design of giant magnetostrictive materials[M]. Beijing: Metallurgical Industry Press, 2003 : 132 -146. (  0) 0)
|
| [6] |
梅德庆, 浦军, 陈子辰. 用于超精密隔振的稀土超磁致伸缩致动器设计[J].
仪器仪表学报,2004, 25 (6) : 766-769.
MEI Deqing, PU Jun, CHEN Zichen. Design of rare earth giant magnetostrictive actuator for ultra-precision vibraion isolation system[J]. Chinese Journal of Scientific Instrument,2004, 25 (6) : 766-769. (  0) 0)
|
| [7] |
HIROYUKI W, MUNEO M. New magnetostrictive type torque sensor for sterring shaft[J].
Sensors and Actuators,2001, 91 (1) : 103-106.
( 0) 0)
|
| [8] |
WANG W J, WANG T Q, TANG J, et al. Design of thin low-frequency smart material based on giant magnetostrictive actuator[J].
Materials Research Innovations,2014, 115 (17) : 299-303.
( 0) 0)
|
| [9] |
ZHU Y C, LI Y S. Development of a deflector-jet electrohydraulic servo-valve using a giant magnetostrictive material[J].
Smart Materials and Structures,2014, 11 (23) : 1-19.
( 0) 0)
|
| [10] |
唐志峰.超磁致伸缩执行器的基础理论与实验研究[D]. 杭州:浙江大学, 2005.
TANG Zhifeng. Funfamental Theory and experiments study of giant magnetostrictive actuator[D]. Hangzhou: Zhejiang University, 2005. (  0) 0)
|
| [11] |
李琳, 陈亮良, 杨勇. 超磁致伸缩作动器的结构分析[J].
北京航空航天大学学报,2013, 39 (9) : 1269-1274.
LI Lin, CHEN Liangyong, YANG Yong. Structural analysis of giant magnetostrictive actuator[J]. Journal of Beijing University of Aeronautics and Astronautics,2013, 39 (9) : 1269-1274. (  0) 0)
|
| [12] |
徐峰, 张虎, 蒋成保, 等. 超磁致伸缩材料作动器的研制及特性分析[J].
航空学报,2002, 23 (6) : 552-555.
XU Feng, ZHANG Hu, JIANG Chenbao, et al. Designing and performance research of giant mgnetostrictive atuator[J]. Acta Aeronautica et Astronautica Sinica,2002, 23 (6) : 552-555. (  0) 0)
|
| [13] |
杨斌堂, 陶华, BONISM. Terfenol-D磁致伸缩微小驱动器磁路设计[J].
机械科学与技术,2005, 24 (3) : 293-295.
YANG Bintang, TAO Hua, BONIS M, et al. Magnetic circuit design for terfenol-D driven gant mgnetostrictive atuator[J]. Mechanical Science and Technology,2005, 24 (3) : 293-295. (  0) 0)
|
| [14] |
张旭辉, 刘永光, 付永领. 磁致伸缩作动器结构优化设计[J].
压电与声光,2009, 31 (3) : 377-380.
ZHANG Xuhui, LIU Yongguang, FU Yongling. Optimum design of the magnetostrictive actuator[J]. Piezoelectrics & Acoustooptics,2009, 31 (3) : 377-380. (  0) 0)
|
| [15] |
王修勇, 姚响宇, 孙洪鑫. 超磁致伸缩作动器有限元建模与磁场分析[J].
土木工程学报,2012, 45 (2) : 172-176.
WANG Xiuyong, YAO Xiangyu, SUN Hongxin. Finite element model of giant magnetostrictive actuator and its magnetic field analysis[J]. China Civil Engineering Journal,2012, 45 (2) : 172-176. (  0) 0)
|
| [16] |
李明范, 项占琴, 吕福在. 超磁致伸缩换能器磁路设计及优化[J].
浙江大学学报,2006, 40 (2) : 193-196.
LI Mingfan, XIANG Zhanqin, LV Fuzai. Magnet circuit design and optimization of giant magnetostrictive transducer[J]. Journal of Zhejiang University,2006, 40 (2) : 193-196. (  0) 0)
|
| [17] |
赵海涛, 何忠波, 李中伟. 超磁致伸缩驱动器磁路优化设计[J].
兵器材料科学与工程,2008, 31 (5) : 72-74.
ZHAO Haitao, HE Zhongbo, LI Zhongwei. Magnetic circuit optimum design for giant magnetostrictive actuator[J]. Ordnance Material Science and Engineering,2008, 31 (5) : 72-74. (  0) 0)
|
| [18] |
李小鹏, 荣凯, 许楠. 超磁致伸缩作动器的磁路设计[J].
天津职业技术师范大学学报,2011, 21 (1) : 19-24.
LI Xiaopeng, RONG Kai, XU Nan. Design of magnetic circuit in giant magnetostrictive device[J]. Journal of Tianjin University of Technology and Education,2011, 21 (1) : 19-24. (  0) 0)
|
| [19] |
牟星, 唐海军, 高学绪, 等. 超磁致伸缩致动器中偏置磁场的有限元模拟[J].
磁性材料及器件,2014, 45 (4) : 6-11.
MU Xing, TANG Haijun, GAO Xuexu, et al. Finite element modeling of magnetic bias field for magnetostrictive actuator[J]. Journal of Magnetic Materials and Devices,2014, 45 (4) : 6-11. (  0) 0)
|
| [20] |
CLARKA E. Magnetostrictive rare Earth-Fe2 compounds[J].
Handbook of Ferromagnetic Materials,1980, 1 : 540-581.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


