在现代无线通讯系统中,通讯信号在干扰环境下的检测和提取是当今研究的热点问题.自适应波束形成技术,为解决这类问题提供一种有效的技术手段,它能在有用信号到达方向形成高增益,在干扰方向形成零陷,从而对干扰信号形成有效抑制,而被广泛应用于导航、雷达、声纳、医学图像等领域.盲自适应波束形成技术能在缺少很多先验信息的情况下形成有用信号的阵列响应.它在抑制干扰、提高追踪性能、降低计算复杂度方面具有重要的研究价值.附加约束条件的自适应波束形成算法按设计准则,主要分为两类:约束最小方差(constrained minimum variance,CMV)准则和约束恒模(constrained constant modulus,CCM)准则.CMV准则是对有用信号的波达角施加约束的情况下使得阵列输出方差最小.CCM准则是使得波束形成的模值输出偏差最小,且对有用信号的阵列输出施加条件约束.随机梯度法 (stochastic gradient,SG)是自适应波束形成的一种经典方法,它通过选取合适的步长,实现对最小均方目标函数的渐近逼近,不需要估计输入信号的协方差矩阵,能有效减少计算量.文献[1]对Bussgan类型的恒模算法给出了步长边界的计算公式;文献[2]利用CMV-SG算法,对CDMA通信系统进行多用户检测,并取得了较好的效果;文献[3]针对不同结构,提出了3种CCM-SG递推算法,并应用于CDMA系统中.该方法的不足是收敛速度慢,而且步长的选取相对困难,步长过小会导致较慢的收敛速度,步长过大又会造成偏差较大,甚至系统不稳定.
在众多自适应波束形成算法中,迭代最小二乘算法[4](recursive least squares,RLS)具有收敛快速性和算法实用性的特点.但该算法存在遗忘因子难以预先确定的问题.文献[5-6]针对这个问题提出可变遗忘因子的RLS算法;文献[7]将CCM-RLS算法应用于智能天线的波束形成中;文献[8]利用CMV-RLS和CCM-RLS算法消除CDMA系统的多径干扰.文献[9]利用UKF算法提出一种自适应盲波束形成算法,但未考虑附加约束条件.本文针对波达角先验信息已知的情况,利用信号的恒模特性,提出一种导向矢量约束的UKF自适应盲波束形成算法.
1 系统模型 1.1 阵列模型定义符号:(·)T为转置运算,(·)H为共轭转置运算,(·)*为共轭运算,In×n为n×n的单位阵,0m×n为m×n的零矩阵,R为实数域,C为复数域.
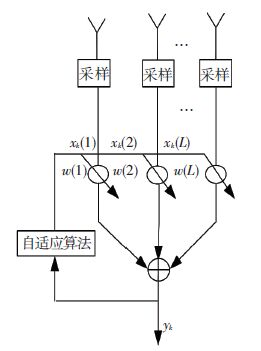
假设信号为点源、远场、传播介质均匀,且传播无衰减.L元传感器阵列如图 1所示,信号的波达角为θi,i=0,1,…,N-1,N为信号数,阵列第k次快拍的接收向量xk∈CL×1为
xk=A(θ)sk+nk,k=1,2,…,M.
|
图 1 自适应波束形成结构 Figure 1 Structure of the adaptive beamformer |
信号的导向矢量矩阵为
A(θ)=[a(θ0),…,a(θN-1)]∈CL×N.
式中:
波束形成的输出为
yk=wHxk.
式中w=[w(1),…,w(L)]T∈CL×1是复权值向量.
1.2 状态空间模型假设存在一个未知系统wk,输入信号xk的阵列响应具有恒模特性,模值为r,则状态空间模型为
| ${{w}_{k}}={{w}_{k-1}},$ | (1) |
| $r=|{{x}^{H}}_{k}{{w}_{k-1}}{{|}^{P}}.$ | (2) |
式中p为一个常数,通常设置为2.
将式(1)、(2)变形可得
| ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}}_{k}}={{A}_{k}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}}_{k}}-1+{{\hat{q}}_{k}}-1$ | (3) |
| ${{y}_{k}}=g({{w}_{k}}\text{-}1).$ | (4) |
式中:
利用式(2)、(4)推得
${\hat{y}}$k(L+1)=r.
w是一个未知向量,${\hat{y}}$k的前L个元素没有参考值,因而,系统引入量测噪声vk.
由式(1)~(4),得到状态空间模型的表达式为
${\hat{w}}$k=Ak${\hat{w}}$k-1+${\hat{q}}$k-1,r=|${\hat{w}}$k-1(L+1)|P+vk.
2 约束自适应波束形成算法约束自适应波束形成算法是通过最小化代价函数,对变量施加条件约束,以获取最优权矢量.写成表达式的形式为
| $w=\left\{ \begin{matrix} minw\text{ }{{J}_{w}}, \\ {{B}^{H}}w=f. \\ \end{matrix} \right.$ |
式中:Jw为代价函数;B∈CL×q为约束矩阵;f∈Cq×1为约束向量.
2.1 CMV算法常用的CMV算法主要包括CMV-SG算法和CMV-RLS算法.CMV-SG算法的代价函数为
| $\left\{ \begin{matrix} {{J}_{w}}={{w}^{H}}_{k}{{x}_{k}}{{x}^{H}}_{k}{{w}_{k}}, \\ {{w}^{H}}_{k}a({{\theta }_{0}})=1. \\ \end{matrix} \right.$ |
运用拉格朗日乘子法可求得递推公式
wk+1=wk-μykH[xk-aH(θ0)xka(θ0)].
式中μ为算法步长.
CMV-RLS算法的代价函数为
| $\left\{ \begin{matrix} {{J}_{w}}=\sum\limits_{l=1}^{k}{{{\alpha }^{k-l}}}{{w}^{H}}_{k}{{x}_{l}}{{x}^{H}}_{l}{{w}_{k}}, \\ {{w}^{H}}_{k}a({{\theta }_{0}})=1. \\ \end{matrix} \right.$ |
式中α为RLS算法的遗忘因子.
运用拉格朗日乘子法可得
wk=[aH(θ0)Rk-1a(θ0)]-1R-1ka(θ0).
通过迭代运算,实现协方差矩阵Rk的求逆运算,由
| ${{R}_{k}}=\sum\limits_{l=1}^{k}{{{\alpha }^{k-l}}}{{x}_{l}}{{x}^{H}}_{l},$ |
运用矩阵求逆引理[10]得
| ${{R}^{-1}}_{k}={{\alpha }^{-1}}{{R}^{-1}}_{k-1}-\frac{{{\alpha }^{-2}}{{R}^{-1}}_{k-1}{{x}_{k}}{{x}^{H}}_{k}{{R}^{-1}}_{k-1}}{1+{{\alpha }^{-1}}{{x}^{H}}_{k}{{R}^{-1}}_{k-1}{{x}_{k}}}.$ |
若令
Pk=R-1k,
则CMV-RLS递推求解公式为
wk=[aH(θ0)Pka(θ0)]-1Pka(θ0).
2.2 CCM算法恒模算法的代价函数为
Jw(p,q)=E[(|yk|p-r)q].
式中:r为信号的恒模值,通常设置为1; p和q为非负常数,通常设置为2; yk表示阵列输出向量y的第k次快拍; E[·]表示期望.
与CMV算法类似,常用的CCM算法包括CCM-SG算法和CCM-RLS算法.CCM-SG算法的代价函数为
| $\left\{ \begin{matrix} {{J}_{w}}={{\left( {{\left| {{y}_{k}} \right|}^{2}}-1 \right)}^{2}}, \\ {{w}^{H}}_{k}a({{\theta }_{0}})=1. \\ \end{matrix} \right.$ |
采用与CMV-SG相似的运算,可得
wk+1=wk-μ(|yk2|-1)ykH×[xk-aH(θ0)xka(θ0)].
CCM-RLS的代价函数为
| $\left\{ \begin{matrix} {{J}_{w}}=\sum\limits_{l=1}^{k}{{{\alpha }^{k-l}}}{{\left[ {{\left| {{w}^{H}}_{k}{{x}_{l}} \right|}^{2}}-1 \right]}^{2}}, \\ {{w}^{H}}_{k}a({{\theta }_{0}})=1. \\ \end{matrix} \right.$ |
运用拉格朗日乘子法,可得
wk=[aH(θ0)Rk-1a(θ0)]-1Rk-1a(θ0).
上式协方差矩阵Rk的求逆,可通过迭代实现,由于
Rk=αRk-1+2[|wkHxl|2-1]xkxkH,
由矩阵求逆引理[10]可得
Rk-1=α-1Rk-1-1-α-1kkxkHRk-1-1.
式中
| ${{k}_{k}}=\frac{{{\alpha }^{-1}}{{P}_{k-1}}{{x}_{k}}}{0.5(|{{w}^{H}}_{k}{{x}_{l}}{{|}^{2}}-1)+{{\alpha }^{-1}}{{x}^{H}}_{k}{{P}_{k-1}}{{x}_{k}}}.$ |
若令
Pk=Rk-1,
则CCM-RLS递推求解公式为
wk=[aH(θ0)Pka(θ0)]-1Pka(θ0).
3 恒模盲波束形成算法 3.1 KF代价函数的最优解因为直接利用1.2节建立的状态空间模型,构造约束UKF的代价函数求解比较困难,本文采用的思路是先对约束条件下的KF构造代价函数,求出最优估计的表达式,再将其推广到约束UKF波束形成算法中.
构造KF代价函数为
| $\left\{ \begin{matrix} min{{J}_{wk}}=[{{({{w}_{k}}-{{{\hat{w}}}_{k|k-1}})}^{H}}{{({{P}_{k|k-1}})}^{-1}}({{w}_{k}}-{{{\hat{w}}}_{k|k-1}})+ \\ {{({{y}_{k}}-{{G}_{k}}{{w}_{k}})}^{H}}{{R}^{-1}}_{k}({{y}_{k}}-{{G}_{k}}{{w}_{k}}))], \\ {{D}_{k-1}}{{w}_{k}}={{d}_{k-1}}. \\ \end{matrix} \right.$ |
式中:wk为系统最优状态估计;${\hat{w}}$k|k-1为KF状态估计的一步预测;Pk|k-1为状态协方差矩阵的一步预测,yk为系统观测输出;Dk-1为状态约束矩阵;dk-1为约束向量;Gk为KF的观测矩阵.
有关KF的详细递推公式可参考文献[11-13].利用拉格朗日乘子法,可求得约束状态估计及其协方差矩阵为
| ${{\hat{w}}^{p}}_{k|k}={{\hat{w}}_{k|k}}+{{K}^{p}}_{k}({{d}_{k-1}}{{\hat{d}}_{k|k-1}}),$ | (5) |
| ${{P}^{wwp}}_{k|k}={{P}_{k|k}}-{{K}^{p}}_{k}{{P}^{dd}}_{k|k}{{K}^{p}}{{_{k}}^{T}}+\delta {{I}_{n\times n}}.$ | (6) |
其中:
${\hat{d}}$k|k-1=Dk-1${\hat{w}}$k|k,
Pk|kdd=Dk-1Pk|kDk-1T,
Pk|kwd=Pk|kDk-1T,
Kkp=Pk|kwd(Pk|kdd)-1.
式中:${\hat{w}}$k|kp为约束状态估计;Kkp为约束增益;${\hat{d}}$k|k-1为约束向量的一步预测;Pk|kwwp为约束状态协方差;Pk|kdd为约束向量协方差;Pk|kwd为约束向量互协方差;δ是为确保Pk|kwwp正定而设置的一个很小的常数.
3.2 UKF约束迭代算法UKF是KF的非线性扩展,是通过UT变换,实现非线性系统线性化的一种近似.该迭代算法是约束KF向非线性约束状态估计的延伸,约束迭代过程如下.
1) 计算sigma点:
| ${{\chi }^{w}}_{k|k}={{{\hat{w}}}_{k|k}}{{1}_{(2n+1)\times 1}}+\sqrt{(n+\lambda )}{{[{{0}_{n\times 1}}{{({{P}_{k|k-1}})}^{\frac{1}{2}}}({{P}_{k|k-1}}))}^{\frac{1}{2}}}].$ | (7) |
2) 传播sigma点:
| ${{\iota }_{j}}({{D}_{k|k}})={{D}_{k|k-1}}{{\iota }_{j}}({{\chi }^{w}}_{k|k}),j=1,\ldots ,2n+1.$ | (8) |
式中ιj(·)表示(·)的第j列元素.
3) 估计约束向量:
| ${{{\hat{d}}}_{k|k-1}}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{(m)}}_{j}{{\iota }_{j}}({{D}_{k|k}}).$ | (9) |
4) 计算协方差矩阵:
| ${{P}^{dd}}_{k|k}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( c \right)}}_{j}[{{\iota }_{j}}({{D}_{k|k}})-{{{\hat{d}}}_{k|k-1}}]{{[{{\iota }_{j}}({{D}_{k|k}})-{{{\hat{d}}}_{k|k-1}}]}^{H}},$ | (10) |
| ${{P}^{wd}}_{k|k}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( c \right)}}_{j}[{{\iota }_{j}}({{\chi }^{w}}_{k|k})-{{{\hat{w}}}_{k|k}}]{{[{{\iota }_{j}}({{D}_{k|k}})-{{{\hat{d}}}_{k|k-1}}]}^{H}}.$ | (11) |
式中γj(m)、γj(c)为UT变换权值分配系数.
3.3 恒模盲波束形成算法的步骤在自适应波束形成算法中,假设阵列波达角θ0为已知的先验信息,则约束条件为
aH(θ0)w=1.
即约束矩阵D=aH(θ0),约束向量d=1.
附加导向矢量约束的UKF波束形成算法主要分为5个环节,第1个环节是迭代参数的初始化;第2个环节为系统的状态预测(步骤1~4);第3个环节为系统的状态更新(步骤5~11);第4个环节是约束迭代过程(步骤12);第5个环节是最优权向量的输出(步骤13~14).详细的求解步骤如下.
首先进行初始化,设定UKF参数ε=1,β=2,κ=0,n=L+1,λ=ε2(n+κ-1)-n+2,γj(m)=
步骤1 选取sigma点:
| ${{\chi }_{k-1|k-1}}={{{\hat{w}}}_{k-1|k-1}}{{1}_{(2n+1)\times 1}}+\sqrt{(n+\lambda )}\times [{{0}_{n\times 1}}{{({{P}_{k-1|k-1}})}^{\frac{1}{2}}}-{{({{P}_{k-1|k-1}})}^{\frac{1}{2}}}].$ |
其中Pk-1|k-1为先验协方差,χk-1|k-1为选取的sigma点.
步骤2 传播sigma点:
| ${{A}_{k}}=\begin{matrix} {{I}_{L\times L}} & {{0}_{L\times 1}} \\ {{x}^{H}}_{k} & 0 \\ \end{matrix},{{\iota }_{j}}({{\chi }_{k|k-1}})={{A}_{k}}{{\iota }_{j}}({{\chi }_{k-1|k-1}}),j=1,\ldots ,2n+1.$ |
步骤3 估计系统状态:
| ${{{\hat{w}}}_{k|k-1}}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( m \right)}}\iota j({{\chi }_{k|k-1}}).$ |
步骤4 估计误差协方差:
| ${{P}_{k|k-1}}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( c \right)}}_{j}\left[ {{\iota }_{j}}({{\chi }_{k|k-1}})-{{{\hat{w}}}_{k|k-1}} \right]\times {{\left[ \iota j({{\chi }_{k|k-1}}){{{\hat{w}}}_{k|k-1}} \right]}^{H}}.$ |
步骤5 计算系统的输出sigma点:
ιj(yk|k-1)=g(ιj(χk|k-1)).
式中函数g(·)表示对ιj(χk|k-1)中的每个元素的绝对值的p次方计算.
步骤6 估计系统输出:
| ${{{\hat{y}}}_{k|k-1}}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{(m)}}_{j}{{\iota }_{j}}({{y}_{k|k-1}}).$ |
步骤7 估计自协方差矩阵:
| $\begin{align} & {{P}^{yy}}_{k|k-1}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( c \right)}}_{j}({{\iota }_{n,j}}({{y}_{k|k-1}}){{{\hat{y}}}_{k|k-1}}[n,1])\times \\ & {{({{\iota }_{n,j}}({{y}_{k|k-1}}){{{\hat{y}}}_{k|k-1}}[n,1])}^{H}}+{{N}_{k}}.{{N}_{k}}={{(\frac{1}{L}\sum\limits_{j=1}^{L}{{{{\hat{y}}}_{k|k-1}}}[j])}^{2}}. \\ \end{align}$ |
式中ιn,j(yk|k-1)为yk|k-1的n行j列元素,${\hat{y}}$k|k-1[n,1]为${\hat{y}}$k|k-1的第n行第1列元素.在阵列维数较高时,噪声参数的调节变得困难,参考文献[9]的方法,对噪声协方差矩阵进行了自适应近似.
步骤8 估计互协方差矩阵:
| ${{P}^{wy}}_{k|k-1}={{\sum\limits_{j=1}^{2n+1}{\gamma }}^{\left( c \right)}}_{j}({{\iota }_{j}}({{\chi }_{k|k-1}}){{{\hat{w}}}_{k|k-1}})\times {{({{\iota }_{n,j}}({{y}_{k|k-1}}){{{\hat{y}}}_{k|k-1}}[n,1])}^{H}}.$ |
步骤9 计算增益矩阵:
| ${{K}_{k}}={{P}^{wy}}_{k|k-1}{{({{P}^{yy}}_{k|k-1})}^{-1}}.$ |
步骤10 计算状态估计:
${\hat{w}}$k|k=${\hat{w}}$k|k-1+Kk(r-${\hat{y}}$k|k-1[n])H.
步骤11 计算误差协方差矩阵: Pk|k=${\hat{p}}$k|k-1-KkPk|k-1yyKHk.
步骤12 利用式(5) ~(11)进行约束迭代.
步骤13 计算系统的最优权值:
w=${\hat{w}}$pk|k(1:L,1).
步骤14 判断是否达到迭代次数.如果是,则算法结束.否则将${\hat{w}}$k|kp、Pk|kwwp返回步骤1,继续迭代.
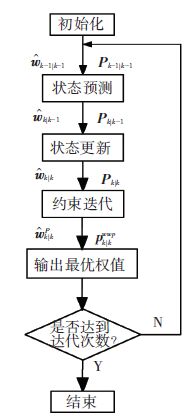
该算法的计算流程如图 2所示.
|
图 2 算法流程图 Figure 2 Algorithm flow chart |
参考文献[7]的对比方式,以信干噪比(signal to interference plus noise ratio,SINR)为指标进行对比仿真,因为文献[2, 7-8]已经验证CCM-RLS和CMV-RLS算法要好于CCM-SG和CMV-SG算法,所以本文仅用所提算法跟文献[7-8]的CCM-RLS,CMV-RLS作对比仿真,来验证算法的性能.
输出SINR的公式为
| ${{S}_{k}}=\frac{{{w}^{H}}_{k}{{R}^{s}}_{k}{{w}_{k}}}{{{w}^{H}}_{k}{{R}^{i+n}}_{k}{{w}_{k}}}.$ |
式中:Rks为有用信号的自相关矩阵,Rki+n为干扰和噪声的互相关矩阵.
一个等距均匀线阵,阵元数L=20,阵元间距为半波长,噪声为高斯白噪声,功率σn2=0.1,对于每次仿真,采用50次蒙特卡洛实验取平均.有用信号的波达角θ0=10°,功率σ02=1.干扰信号方向θ1=43°,干噪比为10 dB,恒模信号选用与文献[4]相同的ejφ(t),φ(t)在[-π,π]服从均匀分布.参考文献[8]的实验,将CCM-RLS、CMV-RLS算法的遗忘因子设置为0.998.
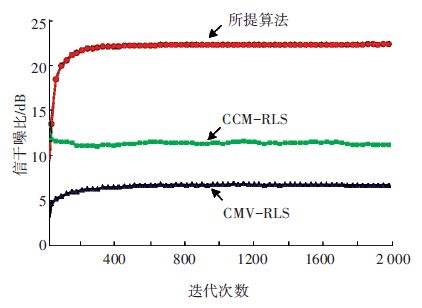
实验1 给出了SINR随快拍数的变化,由图 3可以看出,随着迭代次数的增加,所提算法最终收敛的SINR要高于CMV-RLS和CCM-RLS,而且当迭代次数到达200次时,SINR就可以完全收敛,其他两种算法需要迭代500次以上,由此可见,在收敛速度和收敛的SINR数值上都好于另外两种算法.该仿真也同时验证了CCM-RLS算法性能要好于CMV-RLS,该结论与文献[7-8]一致.
|
图 3 实验1 SINR相对于迭代次数的变化 Figure 3 Exp.1 SINR versus iteration numbers |
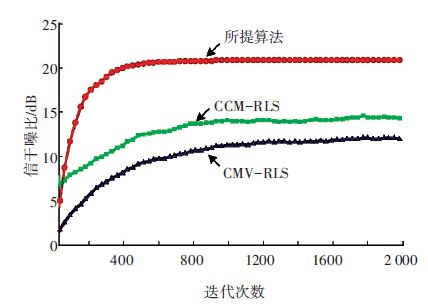
实验2为假定波达角DOA为11°,即存在1°的导向角失配情况,从图 4中可以看出,3种算法存在不同程度的性能下降,但CMV-RLS和CCM-RLS算法性能下降更为明显,而所提算法仍能保持较好的性能,因而所提算法相比于其他两种算法具有较好的稳健性.
|
图 4 实验2 SINR相对于迭代次数的变化 Figure 4 Exp.2 SINR versus iteration numbers |
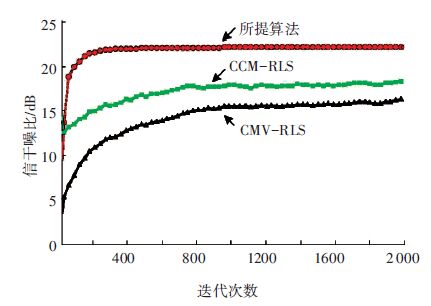
实验3为阵列维数较高时的信干噪比变化情况,此时设定L=60,从图 5中可以看出,CCM-RLS算法收敛SINR为15 dB,CMV-RLS算法的收敛SINR为13 dB,相比于阵列维数较低时,存在着SINR下降的情况,而所提算法在收敛速度和SINR上仍保持较好的性能.
|
图 5 实验3 SINR相对于迭代次数的变化 Figure 5 Exp.3 SINR versus iteration numbers |
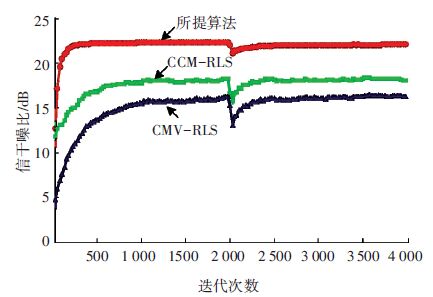
实验4为非平稳条件下的仿真,为了让仿真更加明显,此次仿真将迭代次数增加到了4 000次,并在迭代次数为2 000次时,增加两个INR为3 dB的干扰信号.从图 6可以看出,3种算法在2 000次迭代处都发生了SINR的下降,但相比于其他两种算法,所提算法具有较快的恢复速度,体现出该算法具有较好的跟踪性能和稳态恢复能力.
|
图 6 实验4 SINR相对于迭代次数的变化 Figure 6 Exp.4 SINR versus iteration numbers |
1) 提出一种新型的UKF波束形成算法.先对恒模算法的代价函数进行变形,然后在附加导向矢量约束的条件下,利用UKF的迭代更新等式,求解波束形成器的最优权矢量.
2) 通过数值仿真实验可以得出,相比于经典的CCM-RLS和CMV-RLS算法,该算法具有如下优势:具有较高的输出SINR和较快的收敛速度;在导向角失配情况下表现出较好的稳健性;在阵列维数较高时,仍保持较好的性能指标;在非平稳情况下体现出较好的稳态恢复能力.
| [1] |
ABRAR S, NANDI A K. An adaptive constant modulus blind equalization algorithm and its stochastic stability analysis[J].
IEEE Signal Processing Letters,2010, 17 (1) : 55-58.
DOI: 10.1109/LSP.2009.2031765 ( 0) 0)
|
| [2] |
XU Zhengyuan, TSATSANIS M K. Blind adaptive algorithms for minimum variance CDMA receivers[J].
IEEE Transactions on Communications,2001, 49 (1) : 180-194.
DOI: 10.1109/26.898261 ( 0) 0)
|
| [3] |
MIGUEZ J, CASTEDO L. A linearly constrained constant modulus approach to blind adaptive multiuser interference suppression[J].
IEEE Communications Letters,1998, 2 (8) : 217-219.
DOI: 10.1109/4234.709436 ( 0) 0)
|
| [4] |
CHEN Yuxin, LE NGOC T, CHAMPAGNE B, et al. Recursive least squares constant modulus algorithm for blind adaptive array[J].
IEEE Transactions on Signal Processing,2004, 52 (5) : 1452-1456.
DOI: 10.1109/TSP.2004.826167 ( 0) 0)
|
| [5] |
QIN Boya, CAI Yunlong, CHAMPAGNE B, et al. Low-complexity variable forgetting factor constant modulus RLS-based algorithm for blind adaptive beamforming[J].
Signal Processing,2014, 105 (1) : 277-282.
DOI: 10.1016/j.sigpro.2014.06.003 ( 0) 0)
|
| [6] |
BHOTTO M Z A, ANTONIOU A. New improved recursive least-squares adaptive-filtering algorithms[J].
IEEE Transactions on Circuits and Systems I Regular Papers,2013, 60 (6) : 1548-1558.
DOI: 10.1109/TCSI.2012.2220452 ( 0) 0)
|
| [7] |
WANG Lei, DE LAMARE R C. Blind adaptive beamforming based on constrained constant modulus RLS algorithm for smart antennas[EB/OL]. (2013-03-07)[2015-02-01]. http://arxiv.org/pdf/1303.1848v1/pdf.
( 0) 0)
|
| [8] |
DE LAMARE R C, SAMPAIO NETO R. Blind adaptive MIMO receivers for space-time block-coded DS-CDMA systems in multipath channels using the constant modulus criterion[J].
IEEE Transactions on Communications,2010, 58 (1) : 21-27.
DOI: 10.1109/TCOMM.2010.01.070549 ( 0) 0)
|
| [9] |
BHOTTO M Z A, BAJIC I V. Constant modulus blind adaptive beamforming based on unscented Kalman filtering[J].
IEEE Signal Processing Letters,2015, 22 (4) : 474-478.
DOI: 10.1109/LSP.2014.2362932 ( 0) 0)
|
| [10] |
西蒙.赫金.
自适应滤波器原理[M]. 北京: 电子工业出版社, 2006 : 344 -350.
HAYKIN S. Adaptive filter theory[M]. Beijing: Electronic Industry Press, 2006 : 344 -350. (  0) 0)
|
| [11] |
付梦印, 邓志红, 张继伟.
Kalman滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 2003 : 16 -36.
FU Mengyin, DENG Zhihong, ZHANG Jiwei. Kalman filter theory with applications in navigation system[M]. Beijing: Science Press, 2003 : 16 -36. (  0) 0)
|
| [12] |
JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J].
Proceedings of the IEEE,2004, 92 (3) : 401-422.
DOI: 10.1109/JPROC.2003.823141 ( 0) 0)
|
| [13] |
TEIXEIRA B O S, CHANDRASEKAR J, TORRES L A B, et al. State estimation for linear and non-linear equality-constrained systems[J].
International Journal of Control,2009, 82 (5) : 918-936.
DOI: 10.1080/00207170802370033 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


