2. 中国科学院大学,北京 100039
2. University of Chinese Academy of Sciences, Beijing 100039, China
近些年来,随着终端处理能力以及人们对多媒体体验要求的不断提高,高清视频已经成为多媒体主流趋势[1-3]. 视频信息虽然具有直观性、确定性、高效性等优点,但由于其信息量大,因而在存储和传输方面面临着一些困难[4-5],而现有的H.264编码标准的压缩效率仍然不足以应对高清、超高清视频应用,需要更为高效的编码压缩方案[6]. 为了提升高清视频的编码效率,ISO/IEC运动图像专家组MPEG和ITU-T视频编码专家组VCEG成立了一个视频编码的合作组(JCT-VC)来发展下一代视频编码标准,提出了下一代视频编码标准HEVC [7].
为了对高分辨率视频进行压缩,HEVC使用四叉树编码结构[8],即编码单元(CU),预测单元(PU),变换单元(TU)3个概念描述整个编码过程. 采用这种结构设计的目的是使压缩预测更符合图像特性[9]. HEVC中,每一帧图像首先按顺序被依次分割为64×64大小的最大编码单元(LCU),从LCU开始,根据不同深度,每一个CU可以被递归的分割成4种深度的(64×64,32×32,16×16,8×8)的CU,构成四叉树编码结构.
在每个深度的CU中,从多达35种不同的预测模式中寻找最优模式进行帧内预测编码. 与H.264相比,HEVC编码器大幅提高了预测模式数量,必然导致运算复杂度增加. 因此,提高帧内预测的速度是目前亟待解决的问题. 本文提出了一种基于信息熵的HEVC帧内预测PU分割的尺寸判定算法,可以在保证图像质量的前提下提高编码速度.
1 HEVC帧内预测简介HEVC编码器在进行帧内预测过程中采用遍历搜索方式[10],并利用率失真代价来判定最优候选模式. 在参考软件HM11.0中,率失真代价函数为
| ${{R}_{cost}}={{B}_{mode}}+{{\lambda }_{mode}}\times {{H}_{SSE}}.~$ | (1) |
其中:Bmode为进行每一次模式判决所需要的比特值,HSSE为当前待编码像素块与匹配的像素块差值的平方和,λmode为拉格朗日系数.
在遍历搜索过程中,需要在所有深度等级的CU中寻找率失真代价最低的帧内预测模式,直到CU达到最大深度为止[11]. 这种遍历搜索方式的缺点是:帧内预测虽然提高了预测精度,但也极大地增加了编码复杂度和编码时间. 实际上,图像中纹理平坦的区域更适合用大尺寸CU进行预测,而纹理复杂的区域更适合用小尺寸CU 进行预测. 如果能够利用纹理特性预先判定CU的适当深度,则可跳过不必要的遍历搜索过程,从而节省编码时间.
近些年来,为了减小HEVC编码器的运算复杂度,相关研究者们进行了大量的研究,提出了若干比较有效的算法[12]. Piao等[13]提出了一种算法,通过计算低复杂度率失真代价值和Hadamard变换系数的绝对值之和来预先筛选出帧内预测的最佳候选模式(RMD). Zhao等[14]通过进一步将最可能模式(MPM)引入候选模式从而改进了RMD算法. Xiong等[15]提出一种基于理论分析的算法,利用非归一化的梯度方向直方图来选择最佳编码CU的尺寸. Huang等[16]提出了一种基于方差运算的CU尺寸判定算法,通过设定适当的阈值来决定是否对编码块进行分割. 为了进一步提高编码效率,本文提出了一种基于信息熵的HEVC帧内预测PU的划分尺寸判定算法,在保证图像质量的前提下,减少编码时间. 经过试验证实,相比于现有的分割算法,本文提出的算法在编码时间方面具有一定程度的提升.
2 基于信息熵的帧内预测 2.1 信息熵理论信息熵最早由科学家香农提出,把熵作为一个随机事件发生的不确定性或信息量的量度[17],记信息熵为
| $H\left( X \right)=H({{P}_{1}},{{P}_{2}},\ldots ,{{P}_{n}})=P({{x}_{i}})logP({{x}_{i}}).$ | (2) |
其中:P(xi)为当信源取第i个符号时的概率,i=1,2,…,n;H(X)为信源的信息熵,信息熵具有对称性、非负性、确定性、可加性等[18],本文中主要用到的是信息熵的对称性.
熵的对称性表述为:矢量各分量的次序任意改变时,熵值不变,熵函数的取值仅与概率分布有关. 也就是说,信息熵是整个信元的统计特征的表现,它从平均意义上来度量信源的总体信息量[19]. 图像信息熵是把信息熵公式应用在图像上,设I(Ai)是一个随机变量,i=1,2,…,n,其图像信息熵为
| $H\left( X \right)=\sum\limits_{i=1}^{n}{P\left( {{A}_{i}} \right)}lo{{g}_{2}}\frac{1}{P\left( {{A}_{i}} \right)}=-\sum\limits_{i=1}^{n}{P\left( {{A}_{i}} \right)}lo{{g}_{2}}P({{A}_{i}}).~$ | (3) |
由上式可见,某一随机变量的概率越大,其熵值越小. 数字图像是由一系列的离散像素点构成,灰度值分为256级(0~255),组成集合I,具有灰度j的像素点在图像中出现的概率为Pj,灰度J的信息熵由式(3)得
| $H({{P}_{j}})=-{{P}_{j}}lo{{g}_{2}}({{P}_{j}}),0\le j\le 255.$ | (4) |
不同灰度的熵的累积和为灰度图像的信息熵为
| $E=\sum\limits_{j=0}^{255}{H({{P}_{j}})}=-\sum\limits_{j=0}^{255}{({{P}_{j}})}{{P}_{j}}lo{{g}_{2}}({{P}_{j}})\text{ }.$ | (5) |
对于某一帧给定的图像,信息熵反映了其中包含的灰度信息的均值,通常,图像的细节越少,其中所包含的灰度级越少,则其熵值越小;反之,细节越多,所含灰度级越多,则熵值越大. 当图像为确定的单一灰度(Pi=1),信息熵为0;当图像包含所有256级的灰度,且Pi=Pj时,信息熵最大.
2.2 信息熵在帧内预测方面的应用通过上一小节的分析,利用图像的信息熵来判定图像的平坦程度,通过设定合适的阈值,对PU进行合理分块. 进行帧内预测之前,先计算LCU的信息熵,根据信息熵的结果从64×64至4×4选择最优的分割模式,由于信息熵反映了全局统计特性,不体现图像的空间分布信息,首先利用父块和其4个子块信息熵的结果设定一个阈值,来判定图像的局部统计特性,由此可以判断图像块是否需要进行分割. 另外,通过实验已经证明任何一块复杂的图像,经过不断地分块,其子块的信息熵会接近平坦区的信息熵大小,其纹理复杂程度也会降低,随之信息熵也会降低. 因此,本文的算法提出如下:对每一个LCU进行信息熵的计算,得到的结果与其4个子块的信息熵大小进行比较,如果4个子块的信息熵值大小差异不超过10%,且均小于父块的信息熵,则分割终止,采用父块进行帧内预测与编码;如果任意一个子块的信息熵值比父块信息熵的值大10%,或者任意一个子块的信息熵值与其他子块相比大小超过10%,则该父块需要进行分割,适合采用子块进行帧内预测与编码;以此类推,将上面的子块作为四叉树的根节点,将其信息熵与四叉树子块进行比较,判断是否需要进行分割,直到PU大小为4×4为止. 在这个判定的循环过程中,如果找到了适合进行分割的PU的大小,则跳出循环过程. 在帧内编码过程中,对图像的每一个LCU进行上述判定过程达到提前判断分割大小的目的. 通过这样的判定过程获取每个待编码块的最佳编码深度后,再进行角度预测,可以节省编码时间.
2.3 基于信息熵的分割算法验证对实际的灰度图像进行该算法的分割实验. 任意取一帧灰度图像,截取其中的3个LCU进行试验,如图 1所示. 在图 1中分别取A、B、C 3个LCU,灰度图像如图 2所示.

|
图 1 灰度图像中的3个LCU位置 Figure 1 The position of three LCUs in a grayscale image |

|
图 2 灰度图像中的3个LCU Figure 2 Three LCUs in the grayscale image |
对3个LCU进行上述信息熵判定过程,得到的结果分别如下.
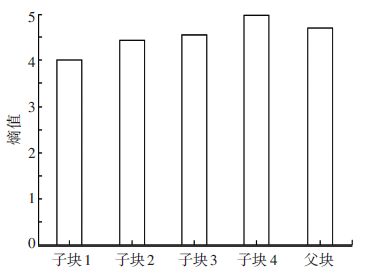
1) 得到的LCU_A的4个子块和A本身的信息熵结果,如图 3所示.
|
图 3 LCU_A中各块信息熵 Figure 3 The subblock entropy values in LCU_A |
信息熵分别为:3.997 9,4.432 5,4.557 3,4.974 9,4.703 3. 由于子块4的信息熵大于父块,需要对子块4进行再分割,得到4个32×32的预测单元(PU),对4个PU进行信息熵计算,得到的结果见表 1.
| 表 1 4个32×32 PU中各子块的信息熵 Table 1 The subblock entropy values of 4 32×32 PU |
由表 1可知,块2的4个16×16子块的信息熵与父块信息熵结果相比较,满足分割终止条件,因此该块适于采用32×32大小的PU进行帧内预测编码,提前跳出分割判定过程;其他3个32×32 PU的各个16×16子块信息熵大小之间差异超过了10%,应进行进一步分割判定. 依次对每个16×16块进行分割信息熵判定,直到满足分割终止的条件最终的分割结果,如图 4所示. 由图 4的分割结果可见,这个LCU所显示的区域是地板,属于一帧图像的背景区域,适合采用较大的32×32,16×16的PU进行编码,而对于地板之间的花纹,需要采用较小的8×8,4×4的PU进行编码.

|
图 4 LCU_A的分割结果 Figure 4 The segmentation of LCU_A |
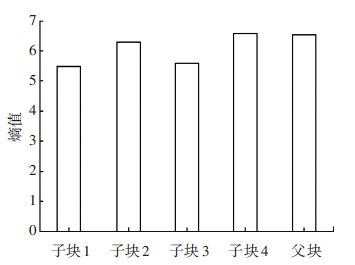
2) 得到的LCU_B的4个子块和B本身的信息熵结果,如图 5所示. 信息熵分别为5.491 4,6.290 7,5.584 6,6.566 7,6.536 9. 其中子块4的信息熵大于父块,需要进行分割,得到4个32×32的PU,对4个PU进行信息熵计算,得到的结果见表 2.
|
图 5 LCU_B中各块信息熵 Figure 5 The subblock entropy values in LCU_B |
| 表 2 4个32×32 PU中各块的信息熵 Table 2 The subblock entropy values of 4 32×32 PUs |
由表 2可知,4个32×32块中的各个16×16子块信息熵大小之间差异超过了10%,都需要进行进一步的分割. 依次对每个16×16块进行分割信息熵判定,直到满足分割终止的条件最终的分割结果如图 6所示. 由图 6的分割结果可见,这个LCU所显示的区域左半边是地板,属于一帧图像的背景区域,适合采用较大的16×16的PU进行编码,而对于地板之间的花纹,需要采用较小的8×8,4×4的PU进行编码;右半部分是运动员的身体,处于运动状态,因此背景区域和运动物体交接处需要采用最小的4×4的PU进行编码,可见信息熵判定的分割效果满足实际需求.

|
图 6 LCU_B的分割结果 Figure 6 The segmentation of LCU_B |
3) 得到的LCU_C的4个子块和C本身的信息熵结果,如图 7所示,信息熵分别为6.334 8,6.378 7,6.872 1,6.480 9,7.094 1. 子块3的信息熵显著大于其他3个子块,需要进行分割处理. 得到4个32×32的PU,对4个PU进行信息熵计算,得到的结果见表 3.

|
图 7 LCU_C中各块信息熵 Figure 7 The subblock entropy values in LCU_C |
| 表 3 4个32×32 PU中各块的信息熵 Table 3 The subblock entropy values of 4 32×32 PUs |
由表 3可知,4个32×32块中的各个16×16子块信息熵大小之间差异超过了10%,都需要进行进一步的分割. 依次对每个16×16块进行分割信息熵判定,直到满足分割终止的条件最终的分割结果如图 8所示. 由图 8的分割结果可见,这个LCU所显示的区域是运动员的头部,图像的背景区域依然是地板,适合采用较大的16×16,8×8的PU进行编码,运动员头部与背景区域交界处属于运动区域,采用最小的4×4的PU进行编码,运动员的面部特征属于一帧图像的细节区域,采用8×8,4×4的PU进行编码.

|
图 8 LCU_C的分割结果 Figure 8 The segmentation of LCU_C |
由上面一帧图像内部的3个处于不同位置,表达不同内容的LCU的分割结果可知,采用信息熵进行图像编码前的PU预先判决是行之有效的.
3 实验结果与分析为了对本文提出的基于信息熵的快速帧内预测算法与标准帧内预测算法进行比较,将本文的算法的功能在HEVC参考软件HM 11.0上实现. 为了客观全面的验证本算法的最终性能,对几个不同纹理特点的标准视频序列分别进行测试. 实验采用全I帧进行编码,编码结构为深度为4,最大LCU为64×64,熵编码采用CABAC结构;测试序列采用JCT-VC推荐的不同分辨率下的各标准测试序列. 表 4列出了本文提出的快速帧内PU分割算法的编码效果,表 5为与其他算法的实验结果对比.
| 表 4 本文算法与标准算法的对比结果 Table 4 Result of the proposed algorithm compared to the standard |
| 表 5 各尺寸测试序列下编码时间的比较 Table 5 Comparison of coding time saving in other algorithm of text sequences |
通过实验发现,对于具有较多的背景区域,且图像中物体运动不是很剧烈的测试序列,如Blowing Bubbles,本算法的加速效果更加明显,这是因为:首先,图像中纹理越平滑,剧烈运动的物体越少,整幅图像中采用小块的PU所占的比例越少,编码器可以减少PU的分割次数,在较大的PU尺寸下跳出分割过程,达到节省编码时间的目的;其次,在本算法中,判断每种PU是否需要分割时,原来的标准算法是4个子块的率失真代价之和与上一级父块的率失真进行比较,而本算法只需进行每个子快与父块信息熵的比较,避免了每一次循环时的数值求和过程,这样也使得整体编码时间有所降低.
由表 4可知,基于信息熵的PU尺寸预测可以在保证图像质量与原算法基本一致的前提下,平均提高了约22.6%的编码速度. 对于分辨率为416×240的“Blowing Bubbles”序列,可以获得最大的编码速度提升,达到了32.5%,编码速度提升最小为分辨率832×480的“Race Horses”,对应速度提升了17.4%. 由于Blowing Bubbles序列中运动物体移动缓慢,而且分辨率不是很高,采用较大尺寸的PU进行帧内预测编码的比例相对较大,跳过了小块PU的判定,因而编码速度提升较明显;“Race Horses”序列中物体运动剧烈,需要更多的小块PU进行编码,在分割判定中占用了较多的时间,所以编码速度提升较慢.
4 结 论1) 针对目前主流的HEVC编码器帧内预测算法速度偏慢的问题,提出一种基于信息熵的HEVC帧内预测单元尺寸快速判定算法. 该算法可使编码器在进行角度预测之前找到最佳帧内预测编码深度,并可以快速判定当前预测单元的尺寸.
2) 图像的信息熵随图像中细节的丰富程度会产生不同的熵值,利用此特性可以作为本算法中图像块快速分割的依据.
3) 使用本算法对HEVC标准视频序列进行测试,试验结果表明:本算法可以在保证图像质量与原算法基本一致的前提下,编码速度平均提升约22.6%,减小了编码器的运算复杂度,节省了帧内预测的编码时间.
| [1] |
GARY J, OHM J, HAN W, et al. Overview of the high efficiency video coding (HEVC) standard[J].
IEEE Transactions on Circuits and Systems for Video Technology,2012, 22 (12) : 1649-1650.
DOI: 10.1109/TCSVT.2012.2221191 ( 0) 0)
|
| [2] |
祝世平, 陈菊嫱. 基于预搜索的高效双目分形视频编码[J].
光学精密工程,2012, 20 (3) : 675-684.
DOI: 10.3788/OPE. ZHU Shiping, CHEN Juqiang. Efficient stereo fractal video coding based on pre-searching[J]. Editorial Office of Optics and Precision Engineering,2012, 20 (3) : 675-684. DOI: 10.3788/OPE. (  0) 0)
|
| [3] |
SHEN Liquan, ZHANG Zhaoyan, AN Pin. Fast CU size decision and mode decision algorithm for HEVC intra coding[J].
IEEE Transactions on Consumer Electronics,2013, 59 (1) : 207-213.
DOI: 10.1109/TCE.2013.6490261 ( 0) 0)
|
| [4] |
赵春蕾, 戴明, 孙丽娜, 等. H.264/AVC码率控制中初始量化参数的估计[J].
光学精密工程,2014, 22 (9) : 2553-2564.
DOI: 10.3788/OPE. ZHAO Chunlei, DAI Ming, SUN Lina, et al. Estimation of initial quantization parameters for H.264/AVC rate contro[J]. Editorial Office of Optics and Precision Engineering,2014, 22 (9) : 2553-2564. DOI: 10.3788/OPE. (  0) 0)
|
| [5] |
吴银花, 金龙旭, 张宁. 针对H.264改进的整像素运动估计算法[J].
光学精密工程,2013, 21 (4) : 1017-1025.
DOI: 10.3788/OPE. WU Yinhua, JIN Longxu, ZHANG Ning. Improvement of fast inter pixel motion estimation algorithm for H.264[J]. Editorial Office of Optics and Precision Engineering,2013, 21 (4) : 1017-1025. DOI: 10.3788/OPE. (  0) 0)
|
| [6] |
温佳, 马彩文, 赵军锁, 等. 自适应提升小波在干涉高光谱压缩中的应用[J].
哈尔滨工业大学学报,2014, 4 (7) : 112-117.
WEN Jia, MA Caiwen, ZHAO Junsuo, et al. An adaptive wavelet transformation used on interference hyperspectral image compression[J]. Journal of Harbin Institute of Technology,2014, 4 (7) : 112-117. (  0) 0)
|
| [7] |
VANNE J, VIITANEN M, TIMO D. Efficient mode decision schemes for HEVC inter prediction[J].
IEEE Transactions on Circuits and Systems for Video Technology,2014, 9 (24) : 1579-1593.
( 0) 0)
|
| [8] |
JANI L, FRANK B, HAN W, et al. Intra coding of the HEVC standard[J].
IEEE Transactions on Circuits and Systems for Video Technology,2012, 22 (12) : 1792-1794.
DOI: 10.1109/TCSVT.2012.2221525 ( 0) 0)
|
| [9] |
CHO S, KIM M. Fast CU splitting and pruning for suboptimal CU partitioning in HEVC intra coding[J].
IEEE Transactions on Circuits and Systems for Video Technology,2013, 23 (9) : 1556-1557.
( 0) 0)
|
| [10] |
WANG Lili, XIU Wanchi. Novel adaptive algorithm for intra prediction with compromised modes skipping and signaling processes in HEVC[J].
IEEE Transactions on Circuits and Systems for Video Technology,2013, 23 (10) : 1687-1689.
( 0) 0)
|
| [11] |
方树青, 郁梅, 徐升阳, 等. 一种HEVC的快速帧间编码新方法[J].
光电子·激光,2015, 26 (5) : 932-939.
FANG Shuqing, YU Mei, XU Shengyang, et al. A novel fast inter coding algorithm for HEVC[J]. Journal of Optoelectronics·Laser,2015, 26 (5) : 932-939. (  0) 0)
|
| [12] |
孙乐, 戴明, 陈晓露, 等. 基于人眼视觉系统的H.264/AVC码率控制算法[J].
光学精密工程,2014, 22 (4) : 1020-1028.
DOI: 10.3788/OPE. SUN Le, DAI Ming, CHEN Xiaolu, et al. H.264/AVC rate control algorithm based on human visual system[J]. Editorial Office of Optics and Precision Engineering,2014, 22 (4) : 1020-1028. DOI: 10.3788/OPE. (  0) 0)
|
| [13] |
PIAO Y, MIN J H, CHEN J. Encoder improvement of unified Intra prediction: JCTVC-C207[S]. Guangzhou: Joint Collaborative Team on Video Coding(JCT-VC) of ITU-T and ISO/IEC, 2010.
( 0) 0)
|
| [14] |
赵亮. HEVC帧内模式决策及其核心技术的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
ZHAO Liang. Researches on fast intra mode decision and core techniques in HEVC[D]. Harbin: Harbin Institute of Technology, 2011. (  0) 0)
|
| [15] |
XIONG Jian. Fast coding unit selection method for high efficiency video coding intra prediction[J].
Optical Engineering,2013, 52 (7) : 1-9.
( 0) 0)
|
| [16] |
HUANG Y, OU T, CHEN H. Fast decision of block size, prediction mode, and intra block for H.264 intra prediction[J].
IEEE Transactions on Circuits and Systems for Video Technology,2010, 20 (8) : 1122-1132.
DOI: 10.1109/TCSVT.2010.2057018 ( 0) 0)
|
| [17] |
BIALYNICKIBIRULA I, MYCIELSKI J. Uncertainty relations for information entropy in wave mechanics[J].
Communications in Mathematical Physics,1975, 44 (2) : 129-132.
DOI: 10.1007/BF01608825 ( 0) 0)
|
| [18] |
CHEN Weiwei, WANG Xuan, MA Jianfeng, et al. Efficient intra prediction algorithm for H.264 based on information entropy[J].
Computer Engineering and Applications,2007, 43 (13) : 114-116.
( 0) 0)
|
| [19] |
谢宏, 程浩忠, 牛东晓. 基于信息熵的粗糙集连续属性离散化算法[J].
计算机学报,2005, 28 (9) : 1570-1574.
XIE Hong, CHENG Haozhong, NIU Dongxiao. Discretization of continuous attributes in rough set theory based on information entropy[J]. Chinese Journal of Computers,2005, 28 (9) : 1570-1574. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


