2. 中国电力科学研究院, 北京 100192
2. China Electric Power Research Institute, Beijing 100192,China
分布式电源在配电网中的广泛接入,为配电网运行优化带来了诸多问题[1]. 如何能够主动管理与同时充分利用现有配电设备提高配网资产利用率,控制DG以应对其高渗透率接入对配电网的影响,是一个亟待解决的问题.
在传统配电网中,通过优化开关开合状态的配电网重构是对配电系统进行运行优化的重要方式. 根据优化时间尺度不同,重构主要包括静态重构[2-3]和动态重构. 静态重构基于确定时间点优化,而动态重构基于时间区段,因此动态重构能够依据负荷的变化对配网结构进行动态调整,保证配电系统的安全、优质、经济运行,更加符合配网日前调度优化要求. 文献[4]利用多代理技术来实现动态重构,把一天分为多个时段,每一个时段由一个工作代理采用静态重构求得一个解集,通过相邻代理间的相互学习对解集进行完善,经协调代理多次迭代获得最终动态重构结果. 文献[5]以降低网损和减少开关操作次数为综合优化目标构建了配电网多目标动态重构模型,设计了一种新型的复合型微分进化多目标优化算法进行求解,解决了群智能进化算法存在的寻优深度与速度之间的矛盾. 文献[6]以一天为优化周期,提出一种计及入网电动汽车和分布式电源的配电系统动态重构模型和求解方法,但是该文献没有考虑将DG作为可调度资源进行调度,仅考虑网络结构的调整.
在配电网中大规模接入DG后,应当对DG,特别是对如微型燃气轮机等可调度DG采取主动的调度管理以充分发挥DG资源的效用. 目前对DG出力调度的研究较少. 文献[7]在电动汽车行驶统计规律的基础上,提出电动汽车与分布式电源协同调度的微网优化调度模型,并给出了微网内所有设备的运行策略,采用CPLEX软件对模型进行求解. 文献[8]提出了DG高渗透率下配电管理系统对DG的短时调度管理模型,分别从日前和实时两个时间尺度对包括燃气轮机、热电联产机组在内的多种可调度DG进行两阶段的调度管理,同时考虑配电网首端有载调压分接头的控制,并采用混合整数线性规划的方法对模型进行求解. 可见,网架结构动态重构和DG有功出力调度是目前对配电网进行运行优化的两个关键技术手段,二者的关系也是相辅相成,互相影响的. 网架结构的变化改变系统中的负荷与DG分布,从而影响DG的出力优化;DG的实时出力变化又会改变配电网潮流的大小和流向,也将对网架结构产生影响. 配电网日前调度既应充分利用已有配网开关设备来优化网络运行,同时又应对新接入的DG采取主动的调度管理[9]. 而目前的文献在研究配电网日前调度问题时都将配电网动态重构和DG出力调度分开考虑,研究二者协调调度的文献很少. 为此,本文的主要创新点是考虑网架结构与可调度DG有功出力协调调度,在日前时间尺度上为配电管理系统建立一套新的有源配电网优化调度方法. 采用改进模糊聚类分析对负荷-DG等值负荷曲线进行时段划分,基于二层规划和机会约束规划建立网架结构与DG出力协调调度模型,根据可调度DG出力优化结果对等值负荷曲线进行动态修正,应用基于解环原则的遗传算法对模型进行求解.
1 配电网网架结构与DG有功出力日前调度架构配电网网架结构与DG有功出力日前调度架构包括数据准备模块、等值负荷曲线时段划分模块、配电网日前调度计算模块和比较模块. 基于不可调度DG与负荷预测值,建立负荷-DG等值负荷曲线. 由于配电系统中开关在短时内不能频繁操作,因此根据等值负荷曲线进行时段划分. 根据时段划分结果,建立网架结构与可调度DG出力协调调度模型,并对模型进行求解得到各时段开关状态与DG出力优化值. 由于各小时可调度DG出力的变化会影响等值负荷曲线的合成,因此根据DG出力的变化动态修正负荷-DG等值负荷曲线,调整负荷分段结果在协调调度模型中重新进行优化计算,如此迭代循环,最终得到最优网架结构与DG出力.
考虑网架结构与可调度DG有功出力动态调整的配电网日前调度具体流程如下.
步骤1 数据准备. 基于历史数据进行未来24 h负荷预测和不可调度DG出力预测. 对不可调度DG出力预测采用文献[3]中的方法.
步骤2 初始等值负荷曲线分段. 根据负荷预测和不可调度DG出力预测结果,可调度DG取额定功率,共同合成初始等值负荷曲线,对初始等值负荷曲线进行时段划分,时段划分结果记为F1.
步骤3 配电网网架结构与DG有功出力日前调度模型计算. 基于等值负荷曲线时段划分结果,建立网架结构与可调度DG出力协调调度模型,求解模型优化开关状态和各小时可调度DG出力值.
步骤4 修正等值负荷曲线分段. 根据优化得到的可调度DG出力值,对等值负荷曲线进行修正,对修正等值负荷曲线进行时段划分,时段划分结果记为F2.
步骤5 判断比较. 比较F1、F2,若F1=F2,优化结束,输出最优网架结构与可调度DG各时段优化出力;若F1≠F2,则将F2的结果赋给F1,进入步骤3.
根据上述步骤,配电网日前优化调度系统流程图如图 1所示.

|
图 1 配电网日前优化调度流程 Figure 1 Flow chart of day-ahead optimal scheduler |
在配电网接入DG渗透率较大的背景下,DG的出力对负荷曲线有很大的影响,因此应将不可调度DG预测出力值、可调度DG的优化出力值以及负荷预测值合成负荷-DG等值负荷曲线. 针对负荷-DG等值负荷曲线,本文采用改进模糊聚类分析法对时段进行划分. 相较于其他分段方法,如单调性分段法[10]、累计增量法等,采用改进模糊聚类分析的方法分段曲线偏差度最小,等值效果更加理想.
2.1 模糊聚类分析聚类分析[11]是求解数据之间相近度的一种有效方法,主要思想是用隶属度来定义变量的隶属类别,根据各变量的最大隶属度进行分类. 设X={x1,x2,…,xn}为待分类样本的集合,n为分类样本个数,模糊聚类的目标函数为
| $min~J\left( U,V \right)=\sum\limits_{k=1}^{n}{\sum\limits_{i=1}^{c}{\|{{x}_{k}}-{{v}_{i}}{{\|}^{2}}}}.$ |
式中:c为聚类个数;m为加权指数,一般取m=2;vi为第i类聚类中心值;uik为样本点xk属于第i类的隶属度;U={uik}为隶属度矩阵;目标函数J(U,V)为各类中样本到聚类中心的加权距离平方和.
2.2 改进模糊聚类分析法时段划分流程应用模糊聚类分析法进行负荷曲线分段时,应基于以下两点进行改进:1)模糊聚类将负荷大小相近的时刻点归为一类,但没有考虑负荷的时序特性,因此需要对聚类结果按时间顺序进行排序来确定负荷曲线的分段数目和各时段起止时刻. 2)在一天内配电网动态重构的次数是有限的,而通过时序排列按类分段所形成的分段数可能大于一天内最大时段划分次数,所以需要通过一定的方法对初始分段进行融合. 采用改进模糊聚类分析对负荷-DG等值负荷曲线进行时段划分的具体步骤如下.
步骤1 基于日前负荷预测值,日前不可调度DG出力预测均值,可调度DG出力值,合成负荷-DG等值负荷曲线. 在本文中,不可调度DG出力预测结果采用多状态模型[3]描述,因此不可调度DG出力预测均值取用各时段DG多状态出力与其概率的乘积和. 在第一次合成负荷-DG等值负荷曲线,可调度DG出力值为其额定功率.
步骤2 负荷数据标准化. 为了减少最小数据和最大数据对聚类影响过大,需要对样本有功负荷数据进行标准化,将聚类数据压缩到[0, 1]闭区间. 标准化公式为
| ${{x}_{i}}=\frac{{{x}_{i}}\prime -min\left\{ {{x}_{i}}\prime \right\}}{max\left\{ {{x}_{i}}\prime \right\}-min\left\{ {{x}_{i}}\prime \right\}}.$ |
式中:xi′为第i个样本点负荷;xi为第i样本点标准化负荷.
步骤3 计算最佳模糊分类矩阵U和聚类中心V[12]. 确定聚类数c,计算获得最佳隶属度矩阵U和聚类中心V,将所有数据按最大隶属度归类获得个时刻负荷所属类别.
步骤4 按照时序进行等值负荷曲线初分段. 记录各时刻样本点的聚类编号,按照时间顺序排列,将同一类且相邻时段汇集成一段,最终形成m1段.
步骤5 比较一天内最大时段划分次数mmax与m1的大小关系. 若mmax≥m1,则最终分段数M=m1;若mmax<m1,则需要对初始分段进行融合. 计算各时段内的等值负荷(负荷均值),比较相邻两段之间的等值负荷差,将差值最小的两段进行融合,此时若分段数m2仍大于mmax,则按照此步骤继续融合,直至mmax=mi.
由于可调度DG的出力不是固定不变的,而是根据调度模型进行优化调整的,可调度DG的出力变化将会影响等值负荷曲线的合成,因此应当根据可调度DG出力的优化调整动态修正等值负荷曲线,具体动态修正步骤在配电网网架结构与DG有功出力日前调度架构中进行了详细的阐述.
3 基于机会约束规划的网架结构与DG出力协调调度二层规划模型 3.1 建模思路基于等值曲线的时段划分结果,为了同时优化未来一天内每个时段的开关状态和DG出力,本文的建模过程主要基于以下两点考虑:1)采用二层规划[13]方法来建立调度模型以实现网架结构和DG出力的协调优化. 根据时段划分结果,首先在上层规划模型中确定每个时段内的开关状态为下层规划提供了初始条件;下层规划模型在上层提供的网架结构下优化各时段内每个小时的可调度DG出力;下层模型得到的DG出力优化值再反馈到上层模型中计算一天内总运行费用,从而实现开关状态和DG出力的协调优化. 在本文中可调DG资源指的是接入10 kV配电网归配电公司所有的DG机组,因此这些DG机组是可调度的. 2)采用机会约束规划来处理不可调度DG随机出力问题[14]. 在本文中,为了体现风力、光伏等不可调度DG出力的随机性,其预测结果取用多状态模型,获得每个小时内风机和光伏的出力及其概率分布,具体方法详见文献[3]. 机会约束规划可以解决在给定置信度水平下具有不确定性因素的优化问题,因此它能够处理多状态模型. 机会约束规划是在约束条件中对随机变量进行在一定置信水平上的决策,与期望值最优的方法相比,机会约束规划的优化结果更具有可信性.
3.2 上层目标函数及约束条件上层建立以日运行费用最小为目标函数的优化模型,依据时段划分结果对每一段内的开关状态进行优化,具体的目标函数为
min Fu=Closs+Cswi+Cfuel+Cpur.
式中:Fu为整个时段(24 h)配电网总的运行费用;Closs为网损费用;Cswi为开关操作费用;Cfuel为可调度DG燃料使用费用;Cpur为从主网总的购电费用.
| ${{C}_{loss}}=\sum\limits_{t=1}^{24}{{{c}_{pur.t}}{{{\bar{P}}}_{loss.t}}\Delta t.}$ |
式中:cpur.t为时段t购电电价;Ploss.t为时段t内满足一定置信水平的等效网络损耗,其取值由下层模型优化返回上层模型;Δt=1 h.
| ${{C}_{swi}}=\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{M}{{{c}_{swi}}\left| {{s}_{ji}}-{{s}_{j(i-1)}} \right|}}.~$ |
式中:N、M分别为支路总数和时段划分后的时段数;cswi为开关操作一次的费用;sji为支路j上的开关在时段i的状态,sji=0表示断开,sji=1表示闭合.
| ${{C}_{fuel}}=\sum\limits_{t=1}^{24}{\underset{j\in U}{\mathop{\sum }}\,}{{c}^{j}}_{fuel}{{F}^{j}}_{fuel.t}.~$ |
式中:U为所有可调度DG的集合;cfuelj为第j个可调度DG单位燃料使用费用;Ffuel.tj为时段t第j个可调度DG所消耗的燃料,其取值由下层模型优化返回上层模型.
| ${{C}_{pur}}=\sum\limits_{t=1}^{24}{{{c}_{pur.t}}}\left( {{P}_{l.t}}-\underset{j\in V}{\mathop{\sum }}\,{{P}^{j}}_{DG.t} \right)\Delta t.$ |
式中:V为系统中所有DG的集合;Pl,t为时段t时的总负荷;PDG.tj为时段t时第j个DG出力.
上层模型满足以下约束条件:1)网络拓扑约束. 网络保持辐射状连通. 2)开关动作次数的限制,其约束公式为
| $\sum\limits_{i=1}^{M}{\left| {{s}_{ji}}-{{s}_{j(i-1)}} \right|}\le {{S}_{jmax}},\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{M}{\left| {{s}_{ji}}-{{s}_{j(i-1)}} \right|}}\le {{S}_{max}}.$ |
式中:Sjmax为单个开关的最大动作次数;Smax为所有开关的最大动作次数.
3.3 下层目标函数及约束条件在下层优化中,从上层已知各个时段的开关状态,在确定的网架结构下,对各个时段内每个小时可调度DG的出力进行优化. 以一个时段内的网络损耗费用、可调度DG的燃料费用和购电费用之和最小为目标函数,对每个时段分别建立下层优化模型. 其中风机、光伏等DG的不可调度出力用机会约束规划的方法处理.
第i时段的目标函数为
| $min~{{F}^{i}}_{d}=\sum\limits_{{{k}_{i}}=1}^{{{L}_{i}}}{\left( {{c}_{pur.{{k}_{i}}}} \right.}\left. \left( {{P}_{l.{{k}_{i}}}}-\sum\limits_{j\in V}{{{P}^{j}}_{DG.{{k}_{i}}}}+{{{\bar{P}}}_{loss.{{k}_{i}}}} \right)\Delta t+\sum\limits_{j\in U}{{{c}^{j}}_{fuel}}{{F}^{j}}_{fuel.{{k}_{i}}} \right).$ |
式中:Fdi为在时段i内配电网的运行费用;Li为时段i内所包含的小时数;cpur.ki为时段i内第ki小时的购电电价;Ploss.ki为时段i内第ki小时满足一定置信水平的等效网络损耗;Ffuel.kij为时段i内第ki小时可调度单元j所消耗的燃料;Pl.ki为时段i内第ki小时的负荷;PDG.kij为时段i内第ki小时第j个DG的有功出力.
下层有模型5个约束条件,分别如下.
1) 网络损耗概率约束为
| $\sum\limits_{\xi =1}^{{{\xi }_{max}}}{P}\left\{ f{{\left( \xi \right)}_{{{k}_{i}}}}\le {{{\bar{P}}}_{loss.{{k}_{i}}}} \right\}\ge \alpha ,f{{\left( \xi \right)}_{{{k}_{i}}}}=\sum\limits_{j=1}^{N}{{{s}^{{{k}_{i}}}}_{j}{{r}_{j}}}({{P}^{{{k}_{i}}}}{{_{\xi j}}^{2}}+{{Q}^{{{k}_{i}}}}{{_{\xi j}}^{2}})/{{U}^{{{k}_{i}}}}{{_{\xi j}}^{2}}.$ |
式中:ξ为多状态系统中的状态变量;ξmax为系统最大状态数;f(ξ)ki为时段i内第ki小时在状态ξ下系统的有功功率损耗值;N为支路总数;sjki为时段i内第ki小时在支路j上的开关的状态,sjki=0表示断开,sjki=1表示闭合;rj为支路j的电阻;Pξj和Qξj分别为时段i内第ki小时状态ξ下支路j的有功功率和无功功率;α为网络损耗的置信水平;Ploss.ki为时段i内第ki小时f(ξ)ki在置信水平至少为α时所取得最小值.
2) 支路功率概率约束为
| $\sum\limits_{\xi =1}^{{{\xi }_{max}}}{P}\left\{ {{P}_{j}}{{\left( \xi \right)}_{{{k}_{i}}}}\le {{P}_{j}}^{max} \right\}\ge {{\beta }_{1}}.$ |
式中:Pj(ξ)ki为时段i内第ki小时在状态ξ下支路j的有功功率值;Pjmax为支路j的有功功率允许最大值;β1为支路功率的置信水平.
3) 节点电压概率约束为
| $\sum\limits_{\xi =1}^{{{\xi }_{max}}}{P}\left\{ {{U}_{l}}^{min}\le {{U}_{l}}{{\left( \xi \right)}_{{{k}_{i}}}}\le {{U}_{l}}^{max} \right\}\ge {{\beta }_{2}}.$ |
式中:Ul(ξ)ki为时段i内第ki小时在状态ξ下节点l的电压值;Ulmax、Ulmin分别为节点l的电压上下限;β2为节点电压的置信水平.
4) 功率平衡约束为
| $\left\{ \begin{matrix} {{P}_{i}}={{U}_{i}}\sum\limits_{j=1}{{{U}_{j}}}({{G}_{ij}}cos{{\delta }_{ij}}+{{B}_{ij}}sin{{\delta }_{ij}}), \\ {{Q}_{i}}={{U}_{i}}\sum\limits_{j=1}{{{U}_{j}}}({{G}_{ij}}sin{{\delta }_{ij}}-{{B}_{ij}}cos{{\delta }_{ij}}). \\ \end{matrix} \right.$ |
式中:Pi、Qi分别为节点i注入的有功功率和无功功率;Gij、Bij、δij依次为节点i、j之间的电导、电纳和电压相角差;n′为系统节点总数;Ui、Uj分别为节点i、j的电压幅值.
5) 可调度DG出力限制为
PDG.lmin≤PDG.l≤PDG.lmax,QDG.lmin≤QDG.l≤QDG.lmax.
式中:PDG.l、QDG.l为节点l处的可调度DG有功、无功出力;PDG.lmin、QDG.lmin分别为节点l处的可调度DG有功、无功出力下限值;PDG.lmax、QDG.lmax分别指节点l处的可调度DG有功、无功出力上限值.
4 配电网网架结构与DG出力协调调度模型求解算法对于配电网网架结构与DG出力协调调度模型,本文应用遗传算法求解. 为了提高算法的收敛性,在上层模型中,基于解环原则指导网络拓扑编码,消除了大量的不可行解,提高算法搜索效率;在下层模型中,对每个小时的可调度DG出力进行二进制编码,采用精英保留策略加速算法收敛.
4.1 基于解环原则的上层拓扑结构编码上层模型针对网络拓扑结构进行编码. 在利用智能优化算法进行配电网重构时,由于产生的解具有随机性,会产生大量不可行解,有可能形成环路或者孤岛,需要对其进行网络拓扑约束检验以确保每个候选解辐射状运行. 解环原则检验能避免产生大量不可行解,提高搜索效率,从而使计算快速有效.
对于配电网来讲,原始辐射状网络为一个树. 每闭合一个联络开关,便构成一个单连支回路. 有n个联络开关,即能形成n条单连支回路. 在本文中,环是指联络开关闭合形成的单连支回路;同环支路是指某两个环的公共支路;同环支路组是指有公共节点的3条支路.
进行配电网重构时,针对联络开关闭合的环,只需把环中的一条支路断开,便能保持该环辐射状运行. 根据此特点,把环内需开断的支路作为染色体的基因,形成的初始候选解染色体表达形式为
[sd1,sd2,…,sdi,…,sdK].
式中:sdi为第i个环内需断开的支路;K为配电系统中环的总数.
针对初始候选解给出如下解环原则:1)重构时每个环中有且只有一条支路解开,不同环之间解开的支路不同. 2)重构时一条同环支路最多只有一条支路解开. 3)重构时一个同环支路组上最多只有两条同环支路解开.
若初始候选解符合以上原则,则该解为可行候选解;否则,则舍弃. 对于M个时段,每个时段选取一个可行候选解共同构建一条上层规划染色体,如图 2所示.

|
图 2 上层规划染色体结构 Figure 2 Chromosome structure of upper level planning |
图 2中edij为在时段j环i处所选取的候选支路. 采用二进制编码,根据各环候选支路条数调整每个基因二进制位数.
4.2 下层规划编码下层模型根据上层所提供的各时段网架结构,对各个时段可调度DG的出力依次进行优化,各个时段优化相对独立. 将某一时段内各个小时的DG有功出力作为控制变量,对其分别编码进行优化,第i时段下层规划染色体如图 3所示.

|
图 3 第i时段规划染色体结构 Figure 3 Chromosome structure of lower level planning at ith segment |
图 3中pikj为i时段中第j小时第k个可调度DG的有功出力. 同样采用二进制编码,将可调度DG有功出力进行离散化处理.
4.3 有源配电网日前优化调度模型计算流程步骤1 输入日前负荷预测值、不可调度DG预测出力及其概率分布、时段划分结果、网络初始数据.
步骤2 利用解环原则检验初始候选解网络拓扑约束,形成可行候选解.
步骤3 从可行候选解中随机产生上层模型初始群体并置上层遗传代数T1=1.
步骤4 对上层各染色体解码确定下层各时段的开关状态. 对下层各个时段依次分别进行优化. 随机产生下层模型初始群体并置下层遗传代数T2=1.
步骤5 针对下层模型中的机会约束规划,计算下层模型目标函数适应度值. 对目标函数和约束条件进行置信水平校验,实施下层遗传操作.
步骤6 进行下层模型终止条件判断,若遗传代数T2大于下层模型最大遗传代数,下层规划模型计算结束,保存下层优化调度结果;否则,T2= T2 +1,转至步骤5.
步骤7 将下层计算所得的每个小时DG出力优化调度值返回到上层规划模型中,计算上层模型目标函数值. 实施上层遗传操作.
步骤8 进行上层模型终止条件判断,若遗传代数T1大于最大遗传代数,计算结束,输出网架结构和DG出力的协调优化结果;否则,T1= T1+1,转至步骤4.
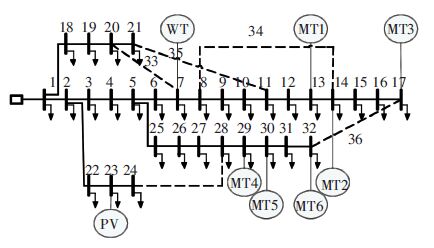
5 算例分析图 4为改进IEEE 33节点配电系统,以此为例探究配电网的日前优化调度问题. 本算例24 h负荷水平取用文献[15]中典型日负荷,具体数值见表 1. 在图 4中,虚线为联络线路,各条支路上均装有开关,7节点处安装风力发电机,其额定功率为400 kW,功率因数为0.9;23节点处安装光伏发电机,其最大输出功率为1 000 kW,功率因数为0.9;13、14、17、29、30、32节点处安装微型燃气轮机,每个节点安装4台,每一台型号均为Capstone C60,其额定有功为60 kW,功率因数0.85,燃料消耗量通过曲线拟合得到计算公式[16]. 天然气价格为1.4元/m3,购电价格为0.5元/kWh,开关操作费用为7元/次[17]. 在本文遗传算法中,上层种群规模为20,遗传代数为50,下层种群规模为50,遗传代数为100. 机会约束规划中的目标函数、支路功率及节点电压的置信水平均取0.9.
|
图 4 IEEE 33节点配电系统 Figure 4 IEEE 33-node distribution system |
| 表 1 模式3各时段优化计算结果 Table 1 The optimal results per hour in model 3 |
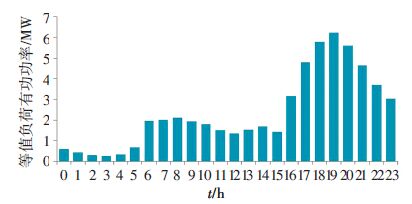
对未来24 h的负荷值、风力发电机出力和光伏发电机出力进行预测,所有微型燃气轮机的输出功率为其额定功率,合成初始负荷-DG等值负荷曲线如图 5所示.
|
图 5 初始负荷-DG等值负荷曲线 Figure 5 Initial equivalent load curve of load-DG |
若设1 d内最大时段划分次数为4次,则根据模糊聚类方法对初始负荷-DG等值负荷曲线进行时段划分的结果如图 6所示.

|
图 6 初始等值负荷曲线时段划分结果 Figure 6 The segment result of initial equivalent load curve |
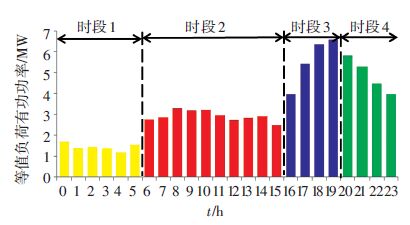
经过协调调度模型计算与修正等值负荷曲线时段划分多次循环迭代,最终负荷-DG等值负荷曲线以及最终时段划分结果如图 7所示.
|
图 7 最终等值负荷曲线时段划分结果 Figure 7 The segment result of ultimate equivalent load curve |
比较图 6、7的分段结果可以发现,初始等值负荷曲线和根据DG出力变化动态修正等值负荷曲线后的分段结果并不一致,说明可调度DG出力的变化会影响时段划分结果,因此需要根据可调度DG出力的变化动态修正等值负荷曲线.
针对配电网的实际情况,进行不同运行模式下优化方案比较分析,提出以下几种不同的运行管理模式:1)网架结构调度模式. 仅对网架结构进行优化调度,可调度DG以其额定出力输出功率. 2)可调度DG调度模式. 仅对可调度DG出力进行优化调度,而网架结构在优化时段内保持不变. 3)可调度DG与网架结构协调调度模式. 即本文所提出的对可调度DG与网架结构进行日前协调调度优化的配电网管理模式.
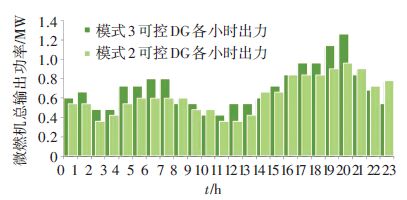
分别对3种模式进行优化计算,得到的结果如图 8、表 1、2所示.
|
图 8 模式2和模式3各时段微燃机优化出力值 Figure 8 The optimal output of micro turbine per hour in model 2 and in model 3 |
| 表 2 各模式优化结果比较 Table 2 The comparison of optimal results from different model |
分析图 8、表 1、表 2中各种模式的优化计算结果,可以发现:1)通过分析表 2,说明在模式1中仅依靠网架重构来优化配电网运行的方式需要更加频繁的开关动作,而在模式3中通过对DG出力进行调度,能减少开关动作次数,延长开关设备的寿命. 2)通过分析图 5,说明在模式3中网架结构的调度能增加系统中DG的渗透率,提高了能源的利用效率,增强了配电网消纳分布式能源的能力. 3)通过分析表 1以及表 2可知,在所有3种模式中模式3的综合运行费用最低,说明用本文方法对配电网的网架结构与可调度DG有功出力进行协调调度能在一定程度改善配电网络的运行状态,提高配电公司的经济效益.
6 结 论1) 在日前时间尺度上研究配电网网架结构和DG有功出力的协调优化调度,建立一套新的有源配电网日前优化调度方法.
2) 可调度DG出力的变化会影响等值负荷曲线时段划分结果,根据可调度DG出力的变化动态修正等值负荷曲线,并采用改进模糊聚类分析进行时段划分,分段结果更为准确,有助于获得最优网架结构调度结果.
3) 采用网架结构与DG出力协调调度的二层规划模型,能够实现开关状态与DG出力的协调优化;同时采用机会约束规划处理不可调度DG随机出力的问题,所得优化结果更具有可信性.
4) 配电网网架结构与DG有功出力协调调度能有效应对负荷变化,在提高配电公司经济效益的基础上,实现配电网资产与DG资源的综合利用. 网络重构与可调度DG的出力调整相互影响:调度DG出力能减少开关动作次数,延长开关设备的寿命;网络重构能增加DG的渗透率,提高能源利用效率,增强了配电网消纳DG的能力.
| [1] |
范明天, 张祖平, 苏傲雪, 等. 主动配电系统可行技术的研究[J].
中国电机工程学报,2013, 33 (22) : 12-18.
FAN Mingtian, ZHANG Zuping, SU Aoxue, et al. Enabling technologies for active distribution systems[J]. Proceedings of the CSEE,2013, 33 (22) : 12-18. (  0) 0)
|
| [2] |
何禹清, 彭建春, 文明, 等. 含风电的配电网重构场景模型及算法[J].
中国电机工程学报,2010, 30 (28) : 12-18.
HE Yuqing, PENG Jianchun, WEN Ming, et al. Scenario model and algorithm for the reconfiguration of distribution network with wind power generators[J]. Proceedings of the CSEE,2010, 30 (28) : 12-18. (  0) 0)
|
| [3] |
丛鹏伟, 唐巍, 张璐, 等. 基于机会约束规划考虑DG与负荷多状态的配电网重构[J].
电网技术,2013 (9) : 2573-2579.
CONG Pengwei, TANG Wei, ZHANG Lu, et al. Chance-constrained programming based distribution network reconfiguration considering multi-states of distributed generation and load[J]. Power System Technology,2013 (9) : 2573-2579. (  0) 0)
|
| [4] |
LI Zhenkun, CHEN Xingying, YU Kun, et al. A novel approach for dynamic reconfiguration of the distribution network via multi-agent system[C]//Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Nanjing: IEEE, 2008: 1305-1311.
( 0) 0)
|
| [5] |
孙惠娟, 彭春华, 袁义生. 综合开关次数分析的配电网多目标动态重构[J].
电力自动化设备,2014, 34 (9) : 41-46.
SUN Huijuan, PENG Chunhua, YUAN Yisheng. Multi-objective dynamic distribution network reconfiguration considering switching frequency[J]. Electric Power Automation Equipment,2014, 34 (9) : 41-46. (  0) 0)
|
| [6] |
陈光, 戴攀, 周浩, 等. 计及入网电动汽车和分布式电源的配电系统重构[J].
电网技术,2013, 37 (1) : 82-88.
CHEN Guang, DAI Pan, ZHOU Hao, et al. Distribution system reconfiguration considering distributed generators and plug-in electric vehicles[J]. Power System Technology,2013, 37 (1) : 82-88. (  0) 0)
|
| [7] |
苗轶群, 江全元, 曹一家. 考虑电动汽车随机接入的微网优化调度[J].
电力自动化设备,2013, 33 (12) : 1-7.
MIAO Yiqun, JIANG Quanyuan, CAO Yijia. Optimal microgrid dispatch considering stochastic integration of electric vehicles[J]. Electric Power Automation Equipment,2013, 33 (12) : 1-7. (  0) 0)
|
| [8] |
BORGHETTI A, BOSETTI M, GRILLO S. Short-term scheduling and control of active distribution systems with high penetration of renewable resources[J].
IEEE Systems Journal,2010, 4 (3) : 313-322.
DOI: 10.1109/JSYST.2010.2059171 ( 0) 0)
|
| [9] |
PILO F, PISANO G, SOMA G G. Optimal coordination of energy resources with a two-stage online active management[J].
Industrial Electronics, IEEE Transactions on,2011, 58 (10) : 4526-4537.
DOI: 10.1109/TIE.2011.2107717 ( 0) 0)
|
| [10] |
尹丽燕, 于继来. 多时间段落的配电网络动态重构[J].
中国电机工程学报,2002, 22 (7) : 44-48.
YIN Liyan, YU Jilai. Dynamic reconfiguration of distribution network with multi-time period[J]. Proceedings of the CSEE,2002, 22 (7) : 44-48. (  0) 0)
|
| [11] |
李培强, 李欣然, 陈辉华, 等. 基于模糊聚类的电力负荷特性的分类与综合[J].
中国电机工程学报,2005, 25 (24) : 73-78.
LI Peiqiang, LI Xinran, CHEN Huihua, et al. The characteristics classification and synthesis of power load based on fuzzy clustering[J]. Proceedings of the CSEE,2005, 25 (24) : 73-78. (  0) 0)
|
| [12] |
林雄, 邢诒杏. 模糊聚类方法在负荷曲线分析中的应用[J].
信息技术,2008, 32 (2) : 94-96.
LIN Xiong, XING Yixing. Application of fuzzy clustering technology in load curves analysis[J]. Information Technology,2008, 32 (2) : 94-96. (  0) 0)
|
| [13] |
范宏, 程浩忠, 金华征, 等. 考虑经济性可靠性的输电网二层规划模型及混合算法[J].
中国电机工程学报,2008, 28 (16) : 1-7.
FAN Hong, CHENG Haozhong, JIN Huazheng, et al. Transmission network bi-level programming model considering economy and reliability and hybrid algorithm[J]. Proceedings of the CSEE,2008, 28 (16) : 1-7. (  0) 0)
|
| [14] |
张璐, 唐巍, 丛鹏伟, 等. 基于机会约束规划和二层规划的配电网广义电源优化配置[J].
电力系统自动化,2014, 38 (5) : 50-58.
ZHANG Lu, TANG Wei, CONG Pengwei, et al. Optimal configuration of generalized power sources in distribution network based on chance constrained programming and bi-level programming[J]. Automatic of Electric Power System,2014, 38 (5) : 50-58. (  0) 0)
|
| [15] |
陈禹, 唐巍, 陈昕玥, 等. 基于负荷-光伏等效负荷曲线动态分段的配电线路联络开关优化配置[J].
电力自动化设备,2015, 35 (3) : 47-53.
CHEN Yu, TANG Wei, CHEN Xinyue, et al. Optimal allocation of tie switch considering load-PV equivalent load curve segment[J]. Electric Power Automation Equipment,2015, 35 (3) : 47-53. (  0) 0)
|
| [16] |
杨艳红, 裴玮, 齐智平. 基于动态运行策略的混合能源微网规划方法[J].
电力系统自动化,2012, 36 (19) : 30-36.
YANG Yanhong, PEI Wei, QI Zhiping. Planning method for hybrid energy microgrid based on dynamic operation strategy[J]. Automatic of Electric Power System,2012, 36 (19) : 30-36. (  0) 0)
|
| [17] |
余贻鑫, 邱炜, 刘若沁. 基于启发式算法与遗传算法的配电网重构[J].
电网技术,2001, 25 (11) : 19-22.
YU Yixi, QIU Wei, LIU Ruoqin. Distribution system reconfiguration based on heuristic algorithm and genetic algorithm[J]. Power System Technology,2001, 25 (11) : 19-22. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


