大口径可展开天线机构可以提高对地观测分辨率水平、卫星通信距离与收发数据容量和精确打击能力等,是航天领域研究的热点之一. 环形桁架式可展开天线的折展比大、质量较小,质量不随口径的增大而成比例的增加,是大口径天线机构的理想结构形式[1-2]. 慕尼黑工业大学与乔治敦大学[3-4]在2012年合作制作了口径为6 m的双环缩放式环形可展桁架,并对该天线机构进行了展开功能试验. Medzmariashvili等[5]提出一种具有V型折叠杆的锥形环形可展桁架,并制作出了口径6 m的试验样机. 当可展开天线口径达到百米量级时,现有结构形式的环形可展开天线的刚度较小,不能满足天线正常工作所需的刚度. 最早的双层桁架概念是由Escrig[6]提出的Pactruss双层环形可展桁架,该结构由内外层环形可展桁架与中央剪式铰联动机构组成. You等[7]提出了一种由双层剪式铰组成的环形机构,其外环和内环单元均为剪式铰机构,由一个剪刀机构实现内环和外环的连接,通过自身安装的小型电机拉动绳索实现整个机构的展收. 关富玲等[8-10]也提出了一种全新构型的双层可展开天线机构,并对其展开过程动力学特性进行了研究. 现有的双层环形可展开天线机构的质量较大,驱动复杂,刚度较小,尚不能完全满足超大口径可展开天线的使用要求,急需提出全新的高刚度、轻量化、无源驱动的双层环形可展开天线机构. Neto等[11]利用多柔体理论研究了柔性机构和卫星二者的耦合动力学特性. Jin等[12]建立了含柔性索网的星载抛物面天线机构多柔体动力学模型,分析了机构展开动力学特性,对索网反射面天线的展开过程进行了仿真. Quisenberry等[13]分别采用有限段法、集中质量法等模拟了柔性索的运动过程. 蒋建平[14]对大挠性卫星刚柔耦合动力学进行了研究,分别采用假设模态法和有限元法,建立了系统刚柔耦合近似动力学方程. 刘钦鹏等[15]利用浮动坐标系进行弹性构件建模,利用拉格朗日方法对展开过程动力学进行了分析. 赵孟良[16]利用广义逆矩阵,发展了展开机构展开运动与弹性变形耦合的分析方法. 刘亮[17]对十二边环形桁架天线模型进行了展开过程动力学分析,提出了动能按余弦规律变化的控制方案,并进行了展开过程试验. 宗亚雳等[18]针对环形可展开天线型面周期性几何逼近误差导致天线远场方向图存在电平较高的栅瓣的问题,提出了通过破坏误差周期性来消除其对电性能影响的方法. 范叶森等[19]提出了一种非对称环形桁架空间索网天线预张力设计的解析算法. 目前,对空间可展开天线机构力学特性的研究多集中在展开动力学特性与索网型面精度的研究上,对于双层环形桁架式可展开天线机构的静力学及展开后动力学特性的研究未见报道,但由于其大尺寸、大柔性的结构特点,其力学特性研究具有重要的意义.
本文综合空间桁架式展开机构及超弹性展开机构的优点,设计一种通过弹性构件驱动展开的高刚度、轻量化、无源驱动的双层环形桁架式可展开天线机构. 建立其静力学分析模型,得出结构中杆件与拉索的相互影响关系,推导对角拉索预紧力的取值范围. 建立双层天线机构的有限元动力学模型,分析采用对角拉索增强结构整体刚度的必要程度. 基于动力学模型,分析纵杆、内外层横杆、连系桁架杆、拉索结构参数及斜拉索拉力等因素对天线结构振动频率的影响.
1 双层环形天线机构设计如图 1所示,双层环形天线机构由内、外层环形机构、内外层连系机构和索网反射面组合而成. 其中,内、外层均为由基本可展开单元沿周向阵列形成的单层环形机构. 连系机构实现了内外层的联动,从而完成双层环形天线机构的展开与收拢.
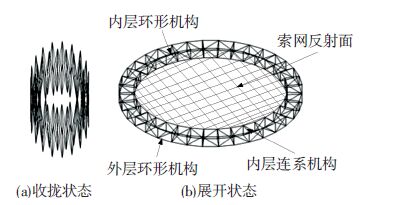
|
图 1 双层环形天线机构组成 Figure 1 The composition of the double-layer hoop deployable antenna mechanism |
为实现双层天线机构的轻量化和无源驱动设计,本文提出图 2所示的由弹性铰链驱动的曲柄滑块式基本可展开单元. 该基本单元包括两根纵向平行设置的支撑杆,4根相同的弦杆. 在机构的转动关节A、B、C、D处分别用弹性铰链连接. 双曲柄滑块机构的两个曲柄分别固连在相邻的两根弦杆上,滑块套装在竖杆上. 两条控速索交叉布置,其一端连接位移补偿弹簧,另一端与电机的驱动端相连接. 整个机构处于收拢状态时,弹性铰链均处于压紧状态. 解除锁定后,上下弦杆在弹性铰链力矩的作用下带动固连在其上的曲柄运动,从而带动滑块在竖杆上滑动,利用双曲柄滑块机构运动过程中两个曲柄转过角度相等的特性实现相邻单元间弦杆运动的同步性,从而实现相邻机构单元的同步展开. 通过对两条释放索的释放速度进行控制,避免因弹性铰链力矩过大而造成冲击碰撞,实现整个机构的平稳展开. 绳索位移补偿弹簧在机构展开锁定完全后,可以通过补偿绳索伸长的位移避免绳索松弛. 当机构完全展开后,上下弦杆之间的弹性铰链利用其自锁特性实现锁定,同时电机反转,对绳索施加一定的预紧力,从而提高整体结构的刚度.
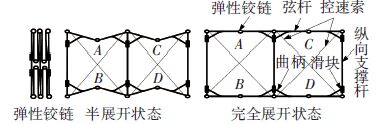
|
图 2 弹性铰链驱动的曲柄滑块式机构单元 Figure 2 Slider-crank mechanism unit driven by the elastic hinges |
弹性铰链可替代传统的弹簧驱动型展开铰链,具有结构简单、质量轻、体积小等特点. 如图 3(a)所示的双片形弹性铰链由两个铰链连接头、2片超弹性带簧片及4个簧片压板组成,具有驱动力距大,展开后可自我锁定的功能.
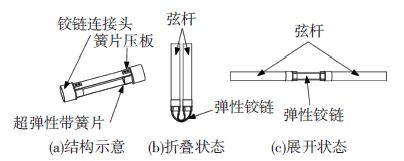
|
图 3 弹性铰链 Figure 3 The elastic hinge |
全弹性铰链驱动的连系机构如图 4所示,其展开原理为:平行四边形的顶点A、B、C、D处为弹性铰链,天线解锁后,弹性铰链利用其储存的弹性势能推动单元展开,展开后通过弹性铰链的自锁性能将节点A、B、C、D锁定,机构单元完成刚化.
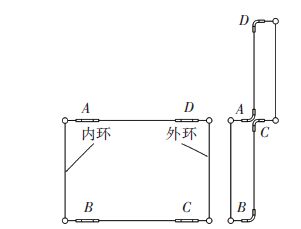
|
图 4 全弹性铰链驱动的连系机构 Figure 4 The linkage mechanism driven by the elastic hinges |
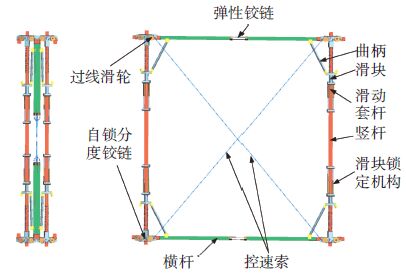
如图 5所示,每个可展开单元由曲柄滑块、自锁铰链、弹性铰链及其所连接的横杆和竖杆所组成,其中包含竖杆2件、横杆4件、弹性铰链2件、自锁分度铰链4件、曲柄滑块机构4件、定滑轮8组、滑动套杆4组、滑块锁定机构4套和控速索2条.
|
图 5 基本单元的结构 Figure 5 The structure diagram of the fundamental unit |
将内外层可展开单元由全弹性铰链连驱动的连系机构相连接即可构成双层环形桁架式可展开天线机构单元,如图 6所示.

|
图 6 双层环形桁架式可展开天线机构单元 Figure 6 The unit of the double-layer hoop truss deployable antenna |
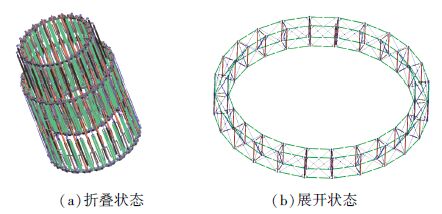
如图 7所示,口径20 m的双层天线机构由24个双层天线机构单元环形阵列构成,其内部组网可用面积可以根据实际使用要求任意设计,收拢体积小,弹性铰链在展开后可自锁,无需额外设计锁定装置,是双层环形桁架式可展开天线机构的理想构型.
|
图 7 口径20 m的双层环形桁架式可展开天线机构 Figure 7 The double-layer hoop truss deployable antenna with the diameter of 20 m |
如图 6所示,为使展开到位后的机构能够拥有足够的刚度,在结构除顶部和底部外的所有一侧均布置对角拉索,并在对角斜拉索上施加一定的预紧力使其始终处于拉紧状态. 预紧力的取值对于结构刚度及结构稳定性至关重要,因此建立双层可展开天线桁架结构单元的静力学分析模型来求取预紧力的取值范围.
整个结构是索杆桁架式自稳定静力平衡结构,拉索预紧力与杆件压力相互平衡,A、B两个节点的受力情况如图 8所示.

|
图 8 单元结构受力 Figure 8 The force conditions of the fundamental unit |
利用节点法分析各杆件的受力情况,A、B点处X、Y、Z方向的合力如式(1)和式(2)所示:
| $\left\{ \begin{array}{l} \sum {F_z} = {F_{{\rm{wb}}}} - {F_{{\rm{s}}{{\rm{w}}_1}}}\cos \beta - {F_{{\rm{s}}{{\rm{w}}_3}}}\cos \beta - \\ {F_{{\rm{s}}{{\rm{w}}_2}}}\cos \alpha = 0,\\ \sum {F_x} = - {F_{{\rm{l}}{{\rm{w}}_3}}} + {F_{{\rm{s}}{{\rm{w}}_2}}}\sin \alpha - {F_{{\rm{l}}{{\rm{w}}_1}}}\sin \left( {180^\circ /n} \right) - \\ {F_{{\rm{l}}{{\rm{w}}_2}}}\sin \left( {180^\circ /n} \right) + {F_{{\rm{s}}{{\rm{w}}_1}}}\sin \beta \sin \left( {180^\circ /n} \right) + \\ {F_{{\rm{s}}{{\rm{w}}_3}}}\sin \beta \sin \left( {180^\circ /n} \right) = 0\\ \sum {F_y} = {F_{{\rm{l}}{{\rm{w}}_2}}}\cos \left( {180^\circ /n} \right) - {F_{{\rm{l}}{{\rm{w}}_1}}}\cos \left( {180^\circ /n} \right) - \\ {F_{{\rm{sw}}}}\sin \beta \cos \left( {180^\circ /n} \right) + {F_{{\rm{s}}{{\rm{w}}_3}}}\sin \beta \cos \left( {180^\circ /n} \right) = 0 \end{array} \right.$ | (1) |
| $\left\{ \begin{array}{l} \sum {F_z} = {F_{{\rm{nb}}}}{F_{{\rm{s}}{{\rm{n}}_1}}}\cos \theta - {F_{{\rm{s}}{{\rm{n}}_3}}}\cos \theta - \\ {F_{{\rm{s}}{{\rm{n}}_2}}}\cos \alpha = 0,\\ \sum {F_x} = {F_{{{\ln }_3}}} - {F_{{\rm{s}}{{\rm{n}}_2}}}\sin \theta - {F_{{{\ln }_1}}}\sin \left( {180^\circ /n} \right) - \\ {F_{{{\ln }_2}}}\sin \left( {180^\circ /n} \right) + {F_{{\rm{sn}}1}}\sin \theta \sin \left( {180^\circ /n} \right) + \\ {F_{{\rm{s}}{{\rm{n}}_3}}}\sin \theta \sin \left( {180^\circ /n} \right) = 0\\ \sum {F_y} = {F_{{{\ln }_2}}}\cos \left( {180^\circ /n} \right) - {F_{{{\ln }_1}}}\cos \left( {180^\circ /n} \right) - \\ {F_{{\rm{s}}{{\rm{n}}_1}}}\sin \theta \cos \left( {180^\circ /n} \right) + \\ {F_{{\rm{s}}{{\rm{n}}_3}}}\sin \theta cos\left( {180^\circ /n} \right) = 0. \end{array} \right.$ | (2) |
事实上,每根对角斜拉索的拉力是可调的,设置其相等,即
| ${F_{{\rm{s}}{{\rm{w}}_1}}} = {F_{{\rm{s}}{{\rm{w}}_2}}} = {F_{{\rm{s}}{{\rm{w}}_3}}} = {F_{{\rm{s}}{{\rm{n}}_1}}} = {F_{{\rm{s}}{{\rm{n}}_2}}} = {F_{{\rm{s}}{{\rm{n}}_3}}} = {F_{\rm{s}}},$ | (3) |
由于各横杆受力相同,则有:${F_{{\rm{l}}{{\rm{w}}_1}}} = {F_{{\rm{l}}{{\rm{w}}_2}}} = {F_{{\rm{lw}}}},{F_{{{\ln }_1}}} = {F_{{{\ln }_2}}} = {F_{\ln }},{F_{{\rm{l}}{{\rm{w}}_3}}} = {F_{{{\ln }_3}}} = {F_{\rm{l}}}$,将式(1)和式(2)化简可得
| $\left\{ \begin{array}{l} {F_{{\rm{wb}}}} = {F_{\rm{s}}}(2\cos b + \cos a),\\ {F_{\rm{l}}} = {F_{\rm{s}}}\sin a - 2{F_{{\rm{lw}}}}\sin \left( {180^\circ /n} \right) + 2{F_{\rm{s}}}\sin b\sin \left( {180^\circ /n} \right), \end{array} \right.$ | (4) |
| $\left\{ \begin{array}{l} {F_{{\rm{nb}}}} = {F_{\rm{s}}}(2\cos \theta + \cos \alpha ),\\ {F_{\rm{l}}} = {F_{\rm{s}}}\sin \theta + 2{F_{\ln }}\sin \left( {180^\circ /n} \right) - 2{F_{\rm{s}}}\sin \theta \sin \left( {180^\circ /n} \right). \end{array} \right.$ | (5) |
由式(4)和式(5)可得每个单元的外内层纵杆的压力分别为
| ${F_{{\rm{wb}}}}c = {F_{\rm{s}}}(2\cos \beta + \cos \alpha ),$ | (6) |
| ${F_{{\rm{nb}}}} = {F_{\rm{s}}}(2\cos \theta + \cos \alpha ).$ | (7) |
由图 8可得知,外层横杆和内层横杆的受力形式完全相同,为了方便后续计算,假设外层横杆受力与内层横杆受力之间的关系为
| ${F_{{\rm{lw}}}} = k\cdot{F_{\ln }}.$ | (8) |
联立式(3) ~ (8)可以求得外层横杆、内层横杆以及连系桁架杆受力分别如式(9)~(11)所示:
| ${{F}_{\text{lw}}}={{F}_{\text{s}}}\frac{k\left[ 2\sin \left( {{180}^{{}^\circ }}/n \right)(\sin \beta +\sin \theta )+\sin \alpha -\sin \theta \right]}{2\left( 1+k \right)\sin \left( {{180}^{{}^\circ }}/n \right)},$ | (9) |
| ${{F}_{\ln }}={{F}_{\text{s}}}\frac{\left[ 2\sin \left( {{180}^{{}^\circ }}/n \right)(\sin \beta +\sin \theta )+\sin \alpha -\sin \theta \right]}{2\left( 1+k \right)\sin \left( {{180}^{{}^\circ }}/n \right)},$ | (10) |
| $\begin{array}{l} {F_{\rm{l}}} = {F_{\rm{s}}}\left\{ {[2\sin \left( {180^\circ /n} \right)(\sin \beta + \sin \theta ) + \sin \alpha - } \right.\\ \left. {\sin \theta ]/\left( {1 + k} \right) + \sin \theta - 2\sin \theta \sin \left( {180^\circ /n} \right)} \right\} \end{array}$ | (11) |
双层环形桁架中的所有杆件均受压力,容易发生失稳. 内外层横杆、纵杆与连系桁架杆均可看成两端铰支的约束形式,长度因数μ=1. 为防止杆件失稳,应有:${F_{{\rm{wb}}}} < {F_{{\rm{wbcr}}}},{F_{{\rm{nb}}}} < {F_{{\rm{nbcr}}}},{F_{{\rm{lw}}}} < {F_{{\rm{lwcr}}}},{F_{ln}} < {F_{\ln {\rm{cr}}}},{F_{\rm{l}}} < {F_{{\rm{lcr}}}}$,其中Fnbcr、 Fwbcr、 Flncr、Flwcr、Flcr分别为内外层纵杆、横杆与连系桁架杆的失稳临界力. 因此,拉索预紧力取值范围如式(12)所示:
| $\begin{array}{l} 0 < {F_{\rm{s}}} < \\ \min \left\{ \begin{array}{l} \min {\pi ^2}{E_l}{I_l}/\left\{ {2l_l^2\left\{ {[2\sin \left( {180°/n} \right)(\sin \beta + } \right.} \right.\\ \sin \theta ) + \sin \alpha - \sin \theta ]/\left( {1 + k} \right) + \\ \left. {\left. {\sin \theta - 2\sin \theta \sin \left( {180°/n} \right)} \right\}} \right\}\\ \frac{{{\pi ^2}{E_{{\rm{wb}}}}{I_{{\rm{wb}}}}}}{{2l_{{\rm{wb}}}^2\left( {2\cos \beta + \cos \alpha } \right)}},\\ \frac{{{\pi ^2}{E_{{\rm{nb}}}}{I_{{\rm{nb}}}}}}{{2l_{{\rm{nb}}}^2\left( {2\cos \theta + \cos \alpha } \right)}},\\ \frac{{{\pi ^2}{E_{{\rm{lw}}}}{I_{{\rm{lw}}}}}}{{2l_{{\rm{lw}}}^2\frac{{k\left[ {2\sin \left( {180°/n} \right)\left( {\sin \beta + \sin \theta } \right) + \sin \alpha - \sin \theta } \right]}}{{2\left( {1 + k} \right)\sin \left( {180°/n} \right)}}}},\\ \frac{{{\pi ^2}{E_{\ln }}{I_{\ln }}}}{{2{l_{{{\ln }^2}}}\frac{{\left[ {2\sin \left( {180°/n} \right)\left( {\sin \beta + \sin \theta } \right) + \sin \alpha - \sin \theta } \right]}}{{2\left( {1 + k} \right)\sin \left( {180°/n} \right).}}}}. \end{array} \right\} \end{array}$ | (12) |
式中:EwbIwb为外层纵杆的抗弯刚度,EnbInb为内层纵杆的抗弯刚度,ElwIlw为外层横杆的抗弯刚度,ElnIln为内层横杆的抗弯刚度,ElIl为连系桁架杆的抗弯刚度,lwb为外层纵杆的长度,lnb为内层纵杆的长度,llw为外层横杆的长度,lln为内层横杆的长度,ll为连系桁架杆的长度.
由式(12)可得出对角斜拉索预紧力的取值范围,为后续双层天线结构动力学特性分析中对角拉索预紧力的取值提供理论支持.
3 双层天线结构动力学建模与分析 3.1 结构动力学建模系统固有模态分析对于结构动力学控制、结构振动破坏及振动主动抑制有着非常重要的指导意义,因此有必要对双层环形桁架式可展开天线结构进行模态分析.
建立无索与含索的双层天线结构的有限元模型,结构中的杆件均采用梁单元模拟. 为真实地模拟含弹性铰链的内外层横杆与连系桁架杆的受力情况,利用与其等质量、等刚度、等几何尺寸的均质梁来进行等效处理,用等效均质梁来建立其有限元仿真模型. 斜拉索采用只能承受拉力的杆单元模拟,通过施加预应力的形式模拟斜拉索100 N的预应力,而角点及滑块用集中质量单元建模.
双层天线结构主要以1根外层纵杆被固定的悬臂梁的形式应用于航天结构中,因此约束一根外层纵杆的6个自由度. 含预应力的双层天线结构的模态分析分为两个步骤,第一步是对整个结构进行静态预应力变形分析;第二步是运用子空间法对整个结构进行考虑预应力状态的模态分析.
采用相同的约束和加载方式,分别计算口径为20 m的无索和含索的双层天线结构的前6阶振动频率及其所对应的振型,其中对角拉索的预紧力为100 N.
3.2 模态分析无索双层天线结构前6阶振型和频率的结果见表 1.
| 表 1 无索双层天线结构前6阶频率及振型 Table 1 The first 6 order frequency and vibration modes of the double-layer antenna structure without ropes |
含索双层天线结构前6阶频率和振型的结果见表 2.
| 表 2 含索双层天线结构前6阶频率及振型 Table 2 The first 6 order frequency and vibration modes of the double-layer antenna structure with ropes |
可见含索双层环形桁架的各阶振型与无索双层环形桁架基本相同,仅在第1阶和第2阶振型出现顺序不同,而含索桁架的振动频率相对于无索桁架提高20%左右,证明对角拉索对双层环形桁架的刚度有很大贡献.
3.3 振动频率影响因素分析由表 2可得含索双层天线结构的前4阶振型分别为面内不对称收缩、面外弯曲、一阶扭转及面内对称收缩,可以很好地表征双层天线结构的面内和面外刚度,因此只对前4阶的模态进行计算与分析.
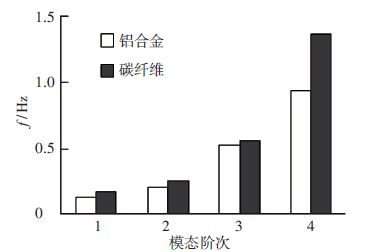
3.3.1 纵杆参数对频率的影响纵杆参数包括纵杆截面直径及纵杆材料参数. 通过有限元仿真分析得到的纵杆直径及纵杆材料对双层天线结构前4阶振动频率的影响见图 9、10.

|
图 9 纵杆直径对频率的影响 Figure 9 The influence of diameter of vertical bar on frequency |
|
图 10 纵杆材料对频率的影响 Figure 10 The influence of materials of vertical bar on frequency |
从图 9可以看出,双层天线结构的1阶振动频率随着纵杆直径的增大而增加,而2、3、4阶振动频率随着纵杆直径的增大而减少,且各阶模态振型对应的振动频率增幅均在10%以内. 其中2阶和3阶振动频率的增幅<2%,1阶振动频率增幅最大,为10.63%.
从图 10中可以看出,碳纤维材料与铝合金相比具有高弹性模量、低密度,因此双层天线结构的弯曲、扭转各阶振动频率均增大,前4阶振动频率分别增加32.75%、25.80%、6.8%和45.53%.
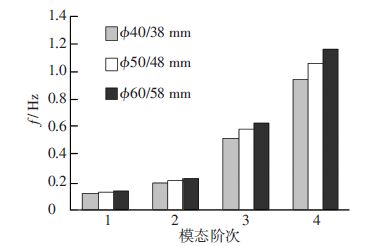
3.3.2 内外层横杆直径对频率的影响从图 11中可以看出,双层天线结构的各阶弯曲振动频率和扭转振动频率随着横杆截面直径的增大而增加. 横杆截面面积变化对1阶和2阶振动频率影响较小,横杆直径从$\phi $40/38增加到$\phi $60/58时,对应的振动频率变化范围在15%之内.
|
图 11 内外层横杆直径对频率的影响 Figure 11 The influence of diameter of inside and outside layer bar on frequency |
内外层横杆材料分别为铝合金、碳纤维时的双层天线结构振动频率变化规律与纵杆的情况一致.
3.3.3 连系桁架杆直径对频率的影响如图 12所示,双层天线结构的各阶弯曲振动频率和扭转振动频率随着连系桁架杆截面直径的增大而增加,对应的振动频率变化范围在9%之内.

|
图 12 连系桁架杆直径对频率的影响 Figure 12 The influence of connecting truss diameter on frequency |
连系桁架杆材料分别为铝合金、碳纤维时的双层天线结构振动频率变化规律与纵杆的情况一致.
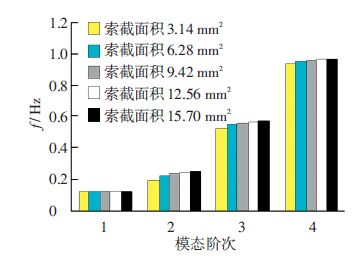
3.3.4 斜拉索参数对频率的影响如图 13所示,随着索截面积的增加,双层天线结构的各阶弯曲振动频率和各阶扭转振动频率不断增大,1阶和4阶振动频率增幅较小,在3%以内,而2阶和3阶振动频率增幅较大,在20%左右. 仿真分析表明,随着索预紧力的增加,双层天线结构的各阶弯曲频率和各阶扭转振动频率几乎没有变化.
|
图 13 索截面积对频率的影响 Figure 13 The influence of cross-sectional area of rope on frequency |
为了便于分析各个结构参数对天线结构各阶固有频率的影响,对天线结构的各参数对整体结构振动频率进行灵敏度分析.
参照文献[20],双层天线结构振动频率fi对参数xi的灵敏度可以表示为
| $\eta ({f_i}/{x_j}) = \mathop {\lim }\limits_{\Delta {x_j} \to 0} \frac{{\Delta f/f}}{{\Delta {x_j}/{x_j}}},({x_j} \ne 0,{f_i} \ne 0).$ | (13) |
式中,fi为双层天线结构的第i阶振动频率,xj为双层天线结构的某一结构参数,Δxj为双层天线结构的某一结构参数的变化量,Δfi为结构参数变化Δxi引起的双层天线结构的第i阶固有频率变化量.
通过上述方法计算出结构参数摄动50%引起双层天线结构4种模态振型所对应的振动频率变化的灵敏度,如表 3所示. 表中的灵敏度负值表示结构的振动频率随结构参数的增加而减小,正值表示结构的振动频率随结构参数的增加而增加.
| 表 3 结构参数摄动50%引起天线结构频率变化的灵敏度 Table 3 The sensitivity of the frequency variation of the antenna structure when the structural parameters change 50% |
从表 3可看出,天线结构面内不对称收缩振型对应的振动频率对横杆截面积最为敏感;对索张力不敏感. 斜拉索截面积对天线结构的面外弯曲振型对应的振动频率影响最大;横杆截面积对结构的一阶扭转振动频率影响较大;横杆截面积对结构的面内对称收缩振动频率影响较大;面外弯曲振型、一阶扭转振型及面内对称收缩振型所对应的振动频率随着纵杆截面面积增加而减小.
综上所述,增加横杆截面面积和斜拉索的截面积,减小纵杆截面面积是提高4种模态振型所对应的振动频率的有效措施.
4 结 论1) 设计了一种由弹性铰链驱动的曲柄滑块式基本可展开单元以及由其组成的双层环形可展开天线机构,实现了超大口径可展开天线机构的轻量化、高刚度、无源驱动设计.
2) 建立了双层天线结构的静力学分析模型,得到了天线结构中杆件与拉索间的相互影响关系,推导了对角斜拉索预紧力的取值范围,为天线机构的工程设计提供了理论基础.
3) 建立了展开后双层天线结构的动力学分析模型,与无拉索相比,通过对角斜拉索刚化可以将结构刚度提高1.2倍.
4) 增加横杆截面面积可以提高双层环形桁架式可展开天线结构面内不对称收缩振型、一阶扭转振型及面内对称收缩振型所对应的振动频率;增加斜拉索的截面积可以提高双层环形桁架式可展开天线结构面外弯曲振型所对应的振动频率;减小纵杆截面面积可以提高双层环形桁架式可展开天线结构面外弯曲振型、一阶扭转振型及面内对称收缩振型所对应的振动频率.
| [1] |
刘荣强, 田大可, 邓宗全. 空间可展开天线结构的研究现状与展望[J].
机械设计, 2010, 27 (9) : 1-10.
LIU Rongqiang, TIAN Dake, DENG Zongquan. Research actuality and prospect of structure for space deployable antenna[J]. Journal of Machine Design, 2010, 27 (9) : 1-10. DOI: 10.13841/j.cnki.jxsj.2010.09.01 |
| [2] |
冯涛, 冀有志, 肖勇, 等. 星载环形天线结构及其应用综述[J].
空间电子技术, 2015 (2) : 22-28.
FENG Tao, JI Youzhi, XIAO Yong, et al. Overview of space-borne perimeter truss antenna and its application[J]. Space Electronic Technology, 2015 (2) : 22-28. DOI: 10.3969/j.issn.1674-7135.2015.02.007 |
| [3] | DATASHVILI L. Foldability of hinged-rod systems applicable to deployable space structures[J]. Ceas Space Journal, 2013, 5 (3) : 157-168. DOI: 10.1007/s12567-013-0052-7 |
| [4] | DATASHVILI L, ENDLERS, WEI B, et al. Study of mechanical architectures of large deployable space antenna apertures: from design to tests[J]. Ceas Space Journal, 2013, 5 (3) : 169-184. DOI: 10.1007/s12567-013-0050-9. |
| [5] | MEDZMARIASHVILI N, MEDZMARIASHVILI E, TSIGNADZE N, et al. Possible options for jointly deploying a ring provided with V-fold bars and a flexible pre-stressed center[J]. CEAS Space Journal, 2013, 5 (3) : 203-210. DOI: 10.1007/s12567-013-0037-6 |
| [6] | ESCRIG F. Expandable space structures[J]. International Journal of Space Structures, 1985, 1 (2) : 79-91. |
| [7] | YOU Z, PELLEGRINO S. Cable-stiffened pantographic deployable structures part 2: mesh reflector[J]. AIAA Journal, 1997, 35 (8) : 1348-1355. DOI: 10.2514/2.243 |
| [8] | YAN X, GUAN F L, XIAN X, et al. Development of a novel double-ring deployable mesh antenna[J]. International Journal of Antennas & Propagation, 2012, 11 (5) : 1497-1500. DOI: 10.1155/2012-375463 |
| [9] |
夏美梦 双圈环形桁架天线索网结构设计与型面精度调整[D]. 杭州:浙江大学,2012.
XIA Meimeng. Design and profile adjustment of cable-net structure of double-loop truss antennas [D]. Hangzhou: Zhejiang University, 2012. |
| [10] |
戴璐. 双环可展开桁架式天线动力学分析与优化设计[D]. 杭州:浙江大学,2014.
DAI Lu. Dynamic analysis and optimal design of double-ring truss deployable antenna[D]. Hangzhou: Zhejiang University, 2014. |
| [11] | NETO M A, AMBROSIO J A C, LEAL R P. Composite materials in flexible multibody systems[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195 (50-51) : 6860-6873. DOI: 10.1016/j.cma.2005.08.009 |
| [12] | JIN M, ANDO K, SENBOKUYA Y, et al. Deployment analysis of large space antenna using flexible multibody dynamics simulation[J]. Acta Astronautica, 2000, 47 (1) : 19-26. DOI: 10.1016/S0094-5765(00)00014-X |
| [13] | QUISENBERRY J E, ARENA A S. Discrete cable modeling and dynamic analysis [C]//Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno: American Institute of Aeronautics and Astronautics Inc, 2006: 18-21. DOI: 10.2514/6.2006-424. |
| [14] |
蒋建平.大挠性多体结构卫星刚柔耦合动力学研究[D].长沙: 国防科学技术大学,2004.
JIANG Jianping. Researches on rigid-flexible coupling dynamics of the flexible multibody satellite [D]. Changsha: National University of Defense Technology, 2004. |
| [15] |
刘钦鹏, 段宝岩, 杨东武. 柔性空间展开机构动力学建模研究[J].
机械设计, 2006, 23 (3) : 1-4.
LIU Qinpeng, DUAN Baoyan, YANG Dongwu. Study on the dynamics modeling of development mechanism in flexible space[J]. Journal of Machine Design, 2006, 23 (3) : 1-4. DOI: 10.13841/j.cnki.jxsj.2006.03.001 |
| [16] |
赵孟良.空间可展结构展开过程动力学理论分析、仿真及试验[D]. 杭州:浙江大学,2007.
ZHAO Mengliang. Dynamic theory analysis, simulation and experiments for deployment process of deployable space structures[D]. Hangzhou: Zhejiang University, 2007. |
| [17] |
刘亮. 桁架可展天线展开过程分析、控制及试验[D]. 杭州:浙江大学,2010.
LIU Liang. Deployment analysis, control and test study for deployable truss antenna [D]. Hangzhou: Zhejiang University, 2010. |
| [18] |
宗亚雳, 王伟, 王从思, 等. 型面周期性误差对环形桁架可展开天线电性能的影响及其消除方法[J].
电子学报, 2014, 42 (5) : 963-970.
ZONG Yali, WANG Wei, WANG Congsi, et al. Effects of periodic geometric error of astro mesh reflector surface on radiation pattern and its elimination method[J]. Acta Electronica Sinica, 2014, 42 (5) : 963-970. DOI: 10.3969/j.issn.0372-2112.2014.05.020 |
| [19] |
范叶森, 李团结, 马小飞, 等. 非对称环形桁架索网天线预张力设计解析算法[J].
哈尔滨工业大学学报, 2015, 47 (1) : 124-128.
FAN Yesen, LI Tuanjie, MA Xiaofei, et al. An analytic algorithm for pretension design of asymmetrical ring truss cable-net antennas[J]. Journal of Harbin Institute of Technology, 2015, 47 (1) : 124-128. DOI: 10.11918/j.issn.0367-6234.2015 |
| [20] | 荣见华. 结构动力修改及优化设计[M]. 2002 : 90 -97. |
 2017, Vol. 49
2017, Vol. 49


