在服务、救援、维修等需要人-机器人交互或配合的任务中,机器人能够跟随所服务或配合的对象是完成此类任务的前提条件.
在以机器人为对象的人体运动重构方面,Kim等[1]与Pollard等[2]利用几何比例调节的方法,实现了人体与机器人运动学匹配;Yamane等[3]和Boutin等[4]基于倒立摆模型在运动重构过程中添加了平衡约束,从而保证机器人的稳定性; Liu等[5]应用ZMP模糊控制器获得运动重构后样本的稳定性; Yi等[6]提出了基于生物力学驱动的扰动恢复控制器,实现了小型仿人机器人在线模仿人体全身运动; Vuga等[7]基于机器人动力学方程的零空间进行运动重构中的平衡调整,该方法能够在平衡条件允许下较好地保留运动相似度;Munirathinam等[8]采用基于连续时间缩放和关节修正的方法,在NAO机器人上复现踢腿动作; Miura等[9]以运动相似度最大化为原则修正步行参数,使HRP-4C机器人动作更加拟人化.
另一方面,Nakazawa等[10]和张利格等[11]将人体运动进行细分整理后拼接成新的运动施加给机器人,前者在HRP机器人上复现了人体舞蹈动作,后者实现了BHR-2机器人刀术表演. 还在一些类似研究[12-15]采用此类划分运动基元的方法,该方法除可对人体动作进行模仿外,还可作为动作识别及新动作拼接生成的基础.
此外,智能算法也被引入到人体步行运动重构之中. Christopher等[16]通过训练与机器人各关节对应的神经网络实现了运动捕捉数据与机器人关节角的匹配; Hwang等[17]利用基于逆运动学神经网络算法减少了运动匹配计算时间; Rempis[18]提出了一种通过稳定步行样本对捕捉样本进行修正的新型神经网络.
为使机器人在满足步行稳定性的同时,尽可能提高运动“相仿性”以完善仿生运动,研究者定义了一些相似性评价:赵晓军等[19]以对应关节角的接近程度衡量运动相似性;张利格等[11]在其基础上加入机器人与人体运动节奏的相似性;柯文德[20]综合考虑运动时空特性与动作节奏提出了相似性定义. 以上相似性分析都集中在关节空间中,未体现机器人与人体运动不同的根本原因,即人体与机器人在肢体长度等运动学参数上的差异.
本文采用几何变换的方法对由三维运动捕捉系统得到的人体步行运动数据进行重构,并考虑机器人关节极限约束得到机器人步行运动样本,构建仿人双足步行机器人样本库,在此基础上提出根据所跟随对象的步行参数在线检索、修正、拼接机器人步行样本以实现机器人实时跟随人步行的方法,并进行了对不同跟随对象的跟随步行实验.
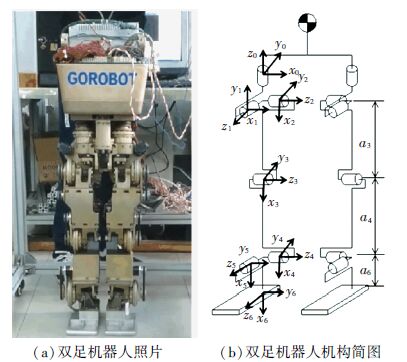
1 仿人双足机器人及运动捕捉系统 1.1 仿人双足步行机器人如图 1(a)所示,所使用的双足机器人为自行研制的类人及类人猿型机器人“GOROBOT-Ⅱ”的双足部分,有12个自由度,髋、膝、踝关节各有3、1、2个自由度,由Maxon伺服电动机+同步齿形带传动+谐波齿轮减速器驱动各个关节,其机构如图 1(b)所示,a3、a4、a6分别为220、184、86 mm,两踝关节间距为125 mm,脚的长、宽为160 mm×100 mm;躯干搭载智能伺服驱动与控制器、电源以及通信模块,质量约22 kg.
|
图 1 GOROBOT-Ⅱ仿人双足步行机器人及其机构图 Figure 1 GOROBOT-Ⅱ humanoid biped robot and its mechanism |
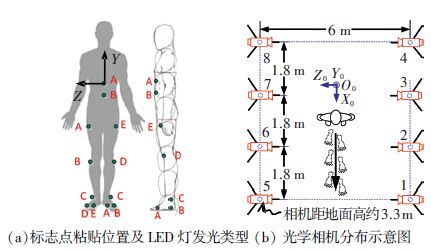
PhaseSpace(PS)三维运动捕捉系统是PhaseSpace公司生产的主动式光学捕捉系统. 其硬件主要包括主机服务器、相机、LED标识点、演出服、校正杆、控制器、基站等. 光学相机分辨率达3 600×3 600 PPI,为双眼结构设计,视角均为60°,扫描速度最高可达480 Hz. 捕捉距离不超过10 m时捕捉精度可达1 mm. 本文用8个相机左右各4个分两列布置,捕捉场景及LED在人身位置如图 2所示.

|
图 2 PS系统对人体步行捕捉场景及LED位置 Figure 2 Scene of human walking captured by PS system and LED distribution demonstration |
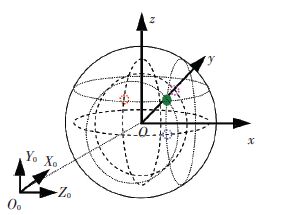
贴于捕捉服上的LED标识点只能布置于关节外侧,因此需根据捕捉数据计算人体关节中心位置,进而确定:大腿、小腿长度、两腿间距、步幅等参数. 由于人体髋、踝关节是侧偏和俯仰运动复合的球形关节,如图 3所示复合运动在二维平面内的投影为近似圆形,半径取决于标识点与关节中心的相对位置.其中,坐标系O0-X0Y0Z0是标定PS系统时确定的世界坐标系,O-xyz为关节中心坐标系,则求关节中心问题转化为已知圆上部分离散点坐标求圆心O坐标(A0,B0,C0)的问题.
|
图 3 世界坐标系内人体运动捕捉的关节运动投影 Figure 3 Joint motion projection of the captured human motion in base coordinate frame |
所捕捉到的标识点坐标以(Xi,Yi,Zi)表示,i=1,2,…,n,设其在X0Y0平面内的投影点分布于圆心为(A0,B0)、半径为R的圆上:
| ${{x}^{2}}+{{y}^{2}}-2{{A}_{0}}x-2{{B}_{0}}y+A_{0}^{2}+B_{0}^{2}-{{R}^{2}}=0.$ | (1) |
若以di表示标志点到圆心的距离,则可定义误差函数σi=di2-R2,将其代入式(1)中,有
| ${{\sigma }_{i}}=X_{i}^{2}+Y_{i}^{2}-2{{A}_{0}}{{X}_{i}}-2{{B}_{0}}{{Y}_{i}}+A_{0}^{2}+B_{0}^{2}-{{R}^{2}}$ |
求解如下无约束最优化问题:
| $\min Q{{A}_{0}},{{B}_{0}}=\sum\limits_{i=1}^{n}{\sigma _{i}^{2}},$ |
可得最优解为
| $\begin{align} & {{A}_{0}}=-\left( HD-EG \right)/(CG-{{D}^{2}})/2, \\ & {{B}_{0}}=-\left( HC-ED \right)/({{D}^{2}}-CG)/2. \\ \end{align}$ |
其中:
| $\begin{align} & C=n\sum\limits_{i=1}^{n}{X_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{X}_{i}}} \right)}^{2}},D=n\sum\limits_{i=1}^{n}{{{X}_{i}}{{Y}_{i}}}-\sum\limits_{i=1}^{n}{{{X}_{i}}}\sum\limits_{i=1}^{n}{{{Y}_{i}}}, \\ & E=n\left( \sum\limits_{i=1}^{n}{X_{i}^{3}}+\sum\limits_{i=1}^{n}{{{X}_{i}}Y_{i}^{2}} \right)-\sum\limits_{i=1}^{n}{\left( {{X}^{2}}_{i}+Y_{i}^{2} \right)}\sum\limits_{i=1}^{n}{{{X}_{i}}}, \\ & G=n\sum\limits_{i=1}^{n}{Y_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{Y}_{i}}} \right)}^{2}}, \\ & H=n\left( \sum\limits_{v}^{n}{Y_{i}^{3}}+\sum\limits_{i=1}^{n}{X_{i}^{2}{{Y}_{i}}} \right)-\sum\limits_{i=1}^{n}{\left( X_{i}^{2}+Y_{i}^{2} \right)}\sum\limits_{i=1}^{n}{{{Y}_{i}}}. \\ \end{align}$ |
对xz、yz、xz平面内标志点投影分别应用上述方法,可求出关节中心的三组圆心坐标,取平均值即为人体关节中心位置坐标. 由关节中心轨迹通过逆运动学可解出各关节角.
2.2 人体步行样本的获取及预处理人体步行捕捉的主要目标为髋、膝、踝三关节的运动,因此设置了如图 4(a)所示的LED粘贴位置,其中字母A~E分别代表贴点处LED灯的发光类型,主动式光学相机布置位置如图 4(b)所示.
|
图 4 LED标识点粘贴位置及主动式光学相机布置示意图 Figure 4 LED location and active optical camera distribution |
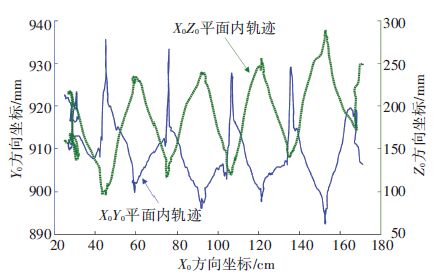
捕捉得到的数据为每个采样时刻各标识点在坐标系O0-X0Y0Z0中的三维坐标值. 图 5为一组捕捉得到的人体髋关节标识点的原始轨迹曲线.
|
图 5 捕捉到的髋关节标识点LED位移原始轨迹 Figure 5 Captured track of the LED located at the hip joint |
捕捉误差及人体抖动使原始轨迹不平滑,且捕捉期间LED标识点被遮挡将使轨迹曲线不连续,因此本文采用拉格朗日线性插值方法对其进行预处理. 利用原始数据可提取人、机器人步行参数(步长、步高、步速、步行周期等),及人体几何特征(肢体长度、踝高、两髋及两踝间的距离等).
3 人体步行样本的运动学匹配人体与机器人机构、几何参数存在差异,因此人体关节角并不能直接施加给机器人,需考虑关节角度、角速度极限等约束条件进行运动学匹配.
3.1 样本的几何缩放匹配设kij为缩放比例,cRk为机器人步行参数,cHk为人体步行参数,则有
| ${{k}_{ij}}={{c}_{\text{R}k}}/{{c}_{\text{H}k}}.$ |
其中i=1,2依次代表髋、踝关节;j=1~3,依次代表前向、侧向和竖直方向;ki1为步长比;ki2为两髋、两踝间距比例;ki3为下肢长度、踝高比例.
设[x y z]T、[x′ y′ z′]T分别为几何缩放前后关节位置矢量,则有如下矩阵变换关系:
| ${{\left[ \begin{matrix} {{x}^{\prime }} & {{y}^{\prime }} & {{z}^{\prime }} \\ \end{matrix} \right]}^{\text{T}}}=\text{diag}({{k}_{i1}},{{k}_{i2}},{{k}_{i3}}){{\left[ \begin{matrix} x & y & z \\ \end{matrix} \right]}^{\text{T}}}.$ |
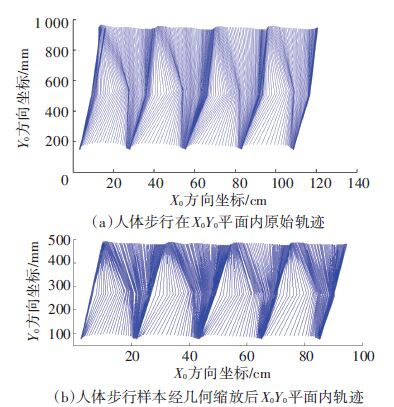
将得到的标志点坐标随踝关节标志点平移至坐标原点O0附近,图 6所示为一组原始人体运动和经比例缩放后机器人运动的棍图轨迹,缩放后基本保持原有的步行周期性特征且步态一致.
|
图 6 人体步行样本按机器人-人几何缩放前后步行轨迹 Figure 6 Walking trajectory of the captured human’s walking pattern before and after the geometric scaling |
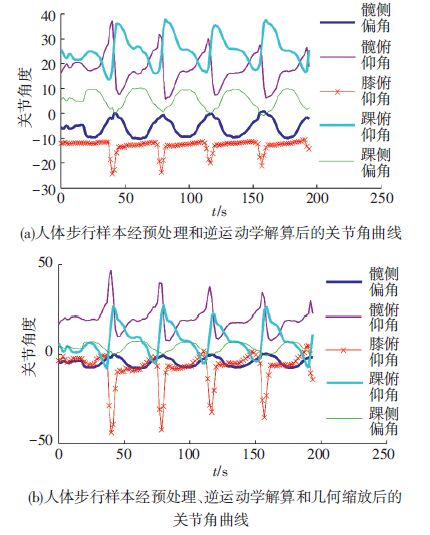
图 7为经预处理和逆运动学解算出的人体运动关节角曲线和经几何缩放及逆运动解算出的机器人关节角曲线,二者关节角呈现出一定差异.
|
图 7 人体步行样本按机器人-人几何缩放前后关节角曲线 Figure 7 Joint angle curves of the captured human’s walking pattern before and after the geometric scaling |
因为实际机器人存在关节角度和角速度极限,所以对比例缩放后的关节角进行约束和过极限处理. 设第i关节的关节角为θi(i=1,2,…,n),关节角速度为${{{\dot{\theta }}}_{i}}$,实际机器人的关节角极限为θimin、θimax;关节角速度极限为${{{\dot{\theta }}}_{i\min }}$、${{{\dot{\theta }}}_{i\max }}$,则需满足如下条件:
| $\begin{align} & {{\theta }_{i\min }}\le {{\theta }_{i}}\le {{\theta }_{i\max }}, \\ & {{{\dot{\theta }}}_{i\min }}\le {{{\dot{\theta }}}_{i}}\le {{{\dot{\theta }}}_{i\max }}. \\ \end{align}$ |
人体在运动时,横滚方向摆动较小,一般不超关节角极限;而俯仰角变化较大,易出现超越机器人关节极限的情况. 髋、膝、踝3个关节的俯仰角分别为θ3、θ4、θ5,机器人在脚底始终保持水平姿势的运动中,有如下关系:
| ${{\theta }_{4}}={{\theta }_{3}}+{{\theta }_{5}}.$ |
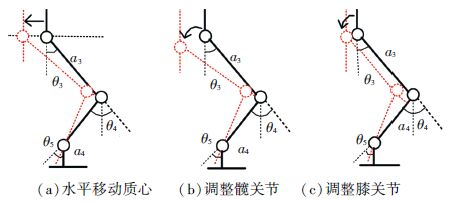
当某关节角超越关节极限时可考虑3种调整方案,这里以踝关节为例进行说明:1)在水平方向微调质心(图 8(a));2)仅调整髋关节俯仰角(图 8(b));3)仅调整膝关节俯仰角(图 8(c)).
|
图 8 机器人关节角超过关节极限的3种处理方式 Figure 8 Three dealing methods of the situation when the joint angle limitation is violated |
通过对比,方案1需要同时调整3个俯仰角,质心速度只有水平分量;方案2、3只需调整两个俯仰角,但质心速度存在竖直分量,削弱了机器人的步行抓地能力,且固定某一关节角不变的条件过于严格. 同时考虑到“GOROBOT-Ⅱ”型机器人踝关节俯仰运动范围可达[-20°~-+75°],因此选择方案1. 调整时首先确定超越关节极限的区间[t1,t3]及达到最大值的时刻t2;而后将t2时刻的θ5调整到关节极限内,并在邻域[t1-ts,t3+ts]内以五次样条插值重新规划θ5以保证区间边界点角度、角速度的连续性.
对角速度超出极限的情况,若${{{\dot{\theta }}}_{5}}$超过角速度极限的区间为[t4,t5],则增加该区间内的关节角样本点间的时间间隔,使其内的关节角速度始终为极限值,而后对该区间重新插值并保持质心高度不变.
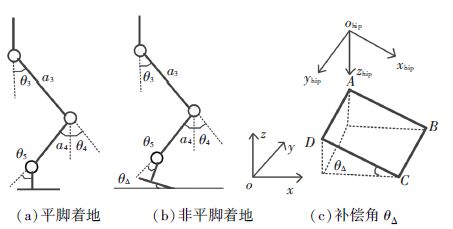
3.3 人体非平脚着地而机器人平脚着地的着地补偿人体步行时非平脚着地,而GOROBOT-Ⅱ型机器人为平板脚掌,行走时需平脚着地. 如图 9所示,需对关节角进行补偿,才能保证机器人平脚步行.
|
图 9 平脚着地、非平脚着地与补偿量θΔ Figure 9 Flat foot landing,tilting foot landing and the compensation angle θΔ |
补偿角θΔ(脚底与地面夹角)有如下关系:
| ${{\theta }_{4}}={{\theta }_{3}}+{{\theta }_{5}}+{{\theta }_{\Delta }}.$ |
本文把各关节角距离关节极限的裕度比例作为分配系数,将θΔ分配给其余关节的俯仰角. 设各关节的调整量为Δθi(i=3,4,5),则有
| $\begin{align} & \Delta {{\theta }_{3}}+\Delta {{\theta }_{4}}+\Delta {{\theta }_{5}}={{\theta }_{\Delta }}, \\ & {{\theta }_{i\min }}\le {{\theta }_{i}}\left( t \right)+\Delta {{\theta }_{i}}\le {{\theta }_{i\max }}, \\ & \Delta {{\theta }_{i}}=({{w}_{i}}/\sum\limits_{i=3}^{5}{\left( {{w}_{i}} \right)}{{\theta }_{\Delta }}. \\ \end{align}$ |
其中:${{w}_{i}}={{\theta }_{\Delta }}/\min \{|{{\theta }_{i}}\left( t \right)-{{\theta }_{i\min }}\left| , \right|{{\theta }_{i}}\left( t \right)-{{\theta }_{i\max }}|\}$.
3.4 步行样本的拟合变换后的原始关节角波动较大,不宜直接施加给机器人,因此对其进行平滑处理,常用的方法有滤波和拟合. 滤波采用平均值滤波,如式(2)所示. 拟合考虑如下3种形式:正弦函数拓展式、高斯函数以及傅里叶函数,如式(3)~(5)所示:
| $\begin{align} & f\left( x \right)=(f(x-n\Delta x)+f(x-\left( n-1 \right)\Delta x)+\cdots + \\ & f(x+n\Delta x))/\left( 2n+1 \right), \\ \end{align}$ | (2) |
| $f\left( x \right)=\sum\limits_{i=1}^{n}{[{{a}_{i}}\sin ({{b}_{i}}x+{{c}_{i}})],}$ | (3) |
| $f\left( x \right)=\sum\limits_{i=1}^{n}{\{{{a}_{i}}{{e}^{-[\left( x-{{b}_{i}} \right)/{{c}_{i}}]}}^{2}\}},$ | (4) |
| $f\left( x \right)={{a}_{0}}+\sum\limits_{i=1}^{n}{[{{a}_{i}}\cos \left( \omega x \right)+{{b}_{i}}\sin \left( \omega x \right)]}.$ | (5) |
大量实验数据的拟合效果证明,从方差和、拟合系数以及均方根误差对这3种拟合形式进行对比来看,正弦函数拓展形式与傅里叶形式对关节角的拟合效果明显优于高斯函数形式;在同等项数下,正弦函数拓展形式的拟合效果优于傅里叶形式. 因此,在拟合形式中,优先选择正弦函数拓展形式(即式(3)). 考虑到人体运动噪声较大以及实验数据的拟合效果,拟合项数选择8项.
4 运动相似性机器人与人运动的差异不仅体现在关节空间的参数上,也体现在笛卡尔空间内的各项参数上,由此选取:笛卡尔空间内的步长、步高、步行周期以及突出步行节奏性差异的“占空比”(单脚支撑期与双脚支撑期的比值)作为关键参数,分别定义S1~S4共4个相似度评价:
| $\begin{align} & {{S}_{1}}=1/\left( 1+\sum\limits_{i=1}^{n}{\left| {{l}_{\text{R}i}}-{{l}_{\text{H}i}} \right|/{{l}_{\text{R}i}}} \right), \\ & {{S}_{2}}=1/\left( 1+\sum\limits_{i=1}^{n}{\left| {{h}_{\text{R}i}}-{{h}_{\text{H}i}} \right|/{{h}_{\text{R}i}}} \right), \\ & {{S}_{3}}={{\left( 1+{{T}_{\text{R}}}-{{T}_{\text{H}}}/{{T}_{\text{R}}} \right)}^{-1}}, \\ & {{S}_{4}}={{\left\{ 1+\frac{{{t}_{\text{SR}}}/{{t}_{\text{DR}}}-{{t}_{\text{SH}}}/{{t}_{\text{DH}}}}{{{t}_{\text{SR}}}/{{t}_{\text{DR}}}} \right\}}^{-1}}. \\ \end{align}$ |
其中:l、h、T、tS、tD分别为步长、步高、步行周期、单脚支撑期、双脚支撑期;下标i=1,2,…,n; n为步行步数.
则笛卡尔空间内运动相似性为
| ${{S}_{\text{C}}}=\sum\limits_{i=1}^{4}{{{\beta }_{i}}{{S}_{i}}}.$ |
其中:βi为[0, 1]范围内的加权系数,且Σβi=1.
在关节空间内选取关节角度和关节角速度衡量相似性,关节空间内的相似性定义为
| ${{S}_{\text{J}}}=\frac{\lambda }{1+\sum\limits_{j=1}^{m}{\frac{\left| {{\theta }_{\text{R}j}}-{{\theta }_{\text{H}j}} \right|}{{{\theta }_{\text{R}j\max }}-{{\theta }_{\text{R}j\min }}}}}+\frac{1-\lambda }{1+\sum\limits_{j=1}^{m}{\frac{\left| {{{\dot{\theta }}}_{\text{R}j}}-{{{\dot{\theta }}}_{\text{H}j}} \right|}{{{{\dot{\theta }}}_{\text{R}j\max }}-{{{\dot{\theta }}}_{\text{R}j\min }}}}}.$ |
式中:λ是取值范围为[0, 1]的权值系数;θ和${\dot{\theta }}$分别为关节角和关节角速度;下标max和min分别表示关节极限最大值和最小值;j=1,2,…,m;m为机器人关节数. 则在笛卡尔空间和关节空间内的综合相似性为
| $S=\alpha {{S}_{\text{C}}}+\left( 1-\alpha \right){{S}_{\text{J}}}$ |
式中:α为笛卡尔空间内相似性的权值系数;S1、S2、S3、S
步行样本库分为两层,即检索表和样本表. 检索表结构如图 10所示. 存储每组样本的步行参数及人体特征信息,为相似样本检索提供评价依据.

|
图 10 步行样本检索表结构 Figure 10 Structure of the walking pattern searching form |
样本表为样本库主体,按检索表顺序存储经过仿真和实验验证能够稳定步行,并由不同被采样者的不同的捕捉数据变换得到的机器人步行样本.
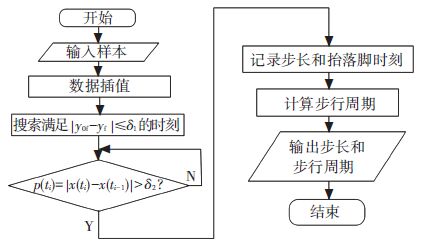
对捕捉原始数据进行插值后提取人体步行参数:步长、步行周期及步速参数. 本文选择粘贴于鞋上的脚部标识点作为关键标识点,将抬脚时刻、抬脚最高时刻以及落地时刻作为步行参数提取的关键姿势帧,并定义人体脚着地的判别条件:
| $\left| {{y}_{0\text{f}}}-{{y}_{\text{f}}} \right|\le \text{ }{{\delta }_{1}}.$ | (6) |
式中:δ1为高度误差限;yf、y0f分别为脚部标识点当前高度和初始高度. 若顺次的两个满足式(6)的时刻脚部标志点在前进方向的距离大于δ2,则确定该距离为步长;这两个时刻依次为该步的抬脚初始时刻和落地时刻;连续两次抬脚时刻差值为步行周期. 设x(ti)、x(ti-1)分别为ti、ti-1时刻标识点前进方向坐标值,则步长判断条件为
| $p({{t}_{i}})=\left| x({{t}_{i}})-x({{t}_{i-1}}) \right|\le {{\delta }_{2}}.$ |
提取人体步行参数的分析过程如图 11所示.
|
图 11 提取人体步行参数的流程图 Figure 11 Process of human walking parameters extraction |
本文以跟随过程中人与机器人之间的距离误差e评价跟随效果,故而定义如下PD控制律:
| $\left\{ \begin{align} & V_{\text{H}}^{'}={{V}_{\text{H}}}+{{K}_{\text{P}}}e+{{K}_{\text{D}}}\dot{e}, \\ & l_{\text{H}}^{'}={{l}_{\text{H}}}{{(V_{\text{H}}^{'}/{{V}_{\text{H}}})}^{-1/2}}, \\ & T_{\text{H}}^{'}=l_{\text{H}}^{'}/V_{\text{H}}^{'}. \\ \end{align} \right.$ |
其中$l_{\text{H}}^{'}T_{\text{H}}^{'}V_{\text{H}}^{'}$分别为目标步长、步行周期、步速;lH、VH分别为提取到的人体步长、步速;KP、KD分别为比例系数、微分系数. 设lj、Tj、Vj分别为机器人步行样本库第j个样本的步长、步行周期、步速,定义相似度评价指标为
| $\begin{align} & {{S}_{\text{ret}}}=\frac{{{\alpha }_{1}}}{1+\left| {{l}_{j}}-l_{\text{H}}^{'} \right|/{{l}_{j}}}+\frac{{{\alpha }_{2}}}{1+\left| {{T}_{j}}-T_{\text{H}}^{'} \right|/{{T}_{j}}}+ \\ & \frac{{{\alpha }_{3}}}{1+\left| {{V}_{j}}-V_{\text{H}}^{'} \right|/{{V}_{j}}}. \\ \end{align}$ |
式中:α1、α2、α3分别为权值系数,α1+α2+α3=1. 步行速度与步长、步行周期相关,且跟随步行强调速度的接近程度,故权值系数中α3取值大于α1、α2.
若有多个样本相似度相同,则比较检索表中人体特征信息与当前被跟踪者的人体特征信息,选择相近的样本,为避免频繁切换步行样本,上述控制过程仅在每个步行周期中进行一次,且选定新样本后计算其与当前样本的相似度值Sf-1,若Sf-1≥β则保留原样本;反之则在下一个步行周期开始更换样本.
5.3 拼接点的查找及运动过渡为完成机器人当前样本到所选样本的样本拼接,需选择合适的拼接点,即机器人姿态具有最大相似性的时刻. 与常用的姿态相似性评价指标如:欧几里得距离、四元数距离[21]以及在动画领域中基于点云的判断方法[22]不同,本文定义“关节角距离”以衡量机器人两个姿态下的关节角的差异:
| ${{Q}_{\text{c}}}=\sum\limits_{i=1}^{5}{{{w}_{ci}}{{\left( ({{\theta }_{i}}-\theta _{i}^{'})/{{\theta }_{i}} \right)}^{2}}}$ |
式中:θi、$\theta _{i}^{'}$分别为两姿态下的机器人关节角,下标i为关节序号;wci为权值系数,取值为[0,1].
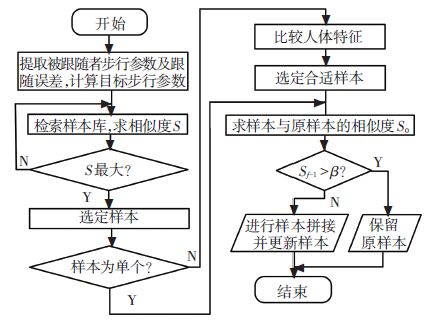
本文将拼接点的查找限定于稳定性较好的双脚支撑期内,选取具有最小关节角距离的时刻作为拼接点. 由于拼接点处机器人的姿态并非完全一致,还需进行两个姿态间的运动过渡. 此过程类似于机器人的轨迹规划,即已知两时刻关节空间内各关节角以及角速度等信息,通过插入新的关节角度,得到完整关节轨迹. 跟随步行控制的流程如图 12所示.
|
图 12 基于样本库的在线步行样本生成流程图 Figure 12 Process of online walking pattern generation based on pattern set |
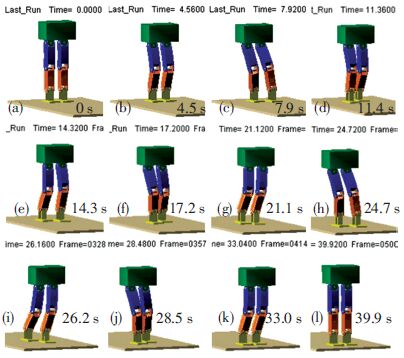
利用ADAMS软件建立GOROBOT-Ⅱ机器人双足部分虚拟样机模型,机器人脚掌与地面之间接触参数设置如表 1所示. 以数据文件形式将机器人-人体运动学匹配生成的步行样本导入ADAMS,进行步行仿真,仿真视频截图见图 13.
| 表 1 机器人脚掌与地面接触参数设置 Table 1 Contact parameter setting between robot’s feet and ground |
|
图 13 运动学匹配后步行样本仿真视频截图 Figure 13 Simulation video capture of a transformed walking pattern example |
本例中步行样本分为加速段、中间步行段和减速段,分别包含下蹲阶段和加速步样本、经运动学匹配后的人体步行循环样本、减速步和身体直立阶段样本,时间分别为11.45、13.80、10.95 s. 由于人体步长不均衡,故经运动学匹配后,步长平均值为200 mm,步行速度为104 m/h.
经仿真验证稳定步行能力后的步行实验如图 14所示,实现稳定步行,则为样本库中成功样本.

|
图 14 离线样本步行实验(一例)视频截图(光滑瓷砖地面) Figure 14 Walking experiment by offline pattern (an example on smooth tile floor) |
跟随步行运动控制按如下步骤进行:1)按采样周期捕捉人体步行样本;2)实时提取人体步行参数;3)在机器人步行样本库中检索相似样本;4)查找拼接点规划过渡轨迹;5)执行新样本,按步行样本的关节轨迹控制机器人跟随人步行.
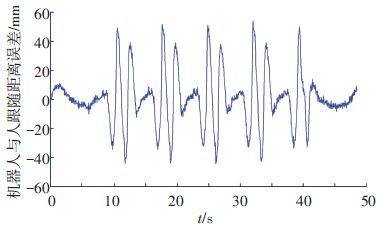
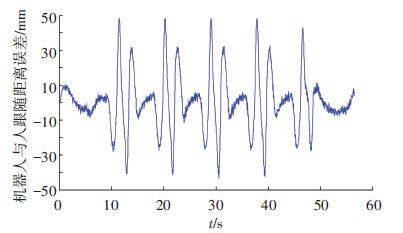
限于篇幅,这里只给出机器人分别跟随两名身高不同并以不同步速前向步行的男性青年人的实验实例,其中机器人腿长490 mm,约为被跟随者腿长的一半. 开始步行时,机器人滞后被跟随者1个周期,以使机器人完成下蹲准备动作,并便于系统提取人体下肢和步行参数,判断人体步行步态特征. 两组实验被跟随者身高分别为1.75、1.78 m;步长均为200 mm;步行周期分别为7.20、8.18 s;步速分别约为100、88 m/h. 机器人的样本轨迹追踪误差的最大值为0.24°,满足步行样本执行的要求. 图 15、16分别为两组实验中机器人跟随人前向步行时的跟随位置误差曲线,最大前向跟随位置误差分别为52、49 mm. 图 17、18分别为这两组跟随步行实验视频截图.
|
图 15 第1组跟随步行实验跟随误差曲线 Figure 15 Following distance error of the first following experiment |
|
图 16 第2组跟随步行实验跟随误差曲线 Figure 16 Following distance error of the second following experiment |

|
图 17 机器人跟随人步行实验视频截图(第1组:跟随身高1.75 m男性青年)(光滑瓷砖地面) Figure 17 Experiment of robot following a human (the first experiment: following a 1.75 m young male on smooth tile floor) |

|
图 18 机器人跟随人步行实验视频截图(第2组:跟随身高1.78 m男性青年)(光滑瓷砖地面) Figure 18 Experiment of robot following a human (the second experiment: following a 1.78 m young male on smooth tile floor) |
1) 基于几何缩放和关节角安全裕度最大的原则,给出了考虑关节角度、角速度极限的由人体运动捕捉数据生成实际机器人可用步行样本的方法,提出了笛卡尔空间、关节空间内机器人-人的运动相似度综合评价指标,提出了基于跟随距离误差和相似样本检索的机器人跟随步行控制方法;
2) 利用PhaseSpace三维运动捕捉系统捕捉了大量人体步行样本,变换为机器人步行样本后经仿真与离线步行实验,实验结果表明,机器人能够稳定步行,验证了基于人体运动捕捉的步行样本生成方法的可行性和有效性,并建立了机器人稳定步行样本库;
3) 进行了在线控制机器人跟随不同步速、不同被跟随者的跟随步行实验,跟随过程中最大跟随距离误差为52 mm,跟随结束后跟随距离误差在±10 mm内,实验验证了机器人实时在线跟随步行控制方法的有效性.
目前,捕捉得到不同身高不同步速人的步行样本较丰富,但经离线样本步行实验验证有效的样本还有限,后续尚需经大量的机器人步行实验验证后扩充样本库,并且进一步研究快速跟随步行下,在线调整拼接相似性样本对步行稳定性的影响.
| [1] | KIM J Y, KIM Y S. Walking pattern mapping algorithm using fourier fitting and geometric approach for biped humanoid robots[C]//Proc 9th IEEE-RAS Conf on Humanoid Robots. Piscataway: IEEE Press, 2009: 243-249. DOI:10.1109/ICHR.2009.5379571. |
| [2] | POLLARD N S, HODGINS J K, RILEY M J, et al. Adapting human motion for the control of a humanoid robot[C]//Proc 2002 IEEE Conf on Robotics and Automation. Piscataway: IEEE Press, 2002: 1390-1397. DOI:10.1109/ROBOT.2002.1014737. |
| [3] | YAMANE K, HODGINS J. Control-aware mapping of human motion data with stepping for humanoid robots[C]//Proc 2010 IEEE-RSJ Conf on Intelligent Robots and Systems. Piscataway: IEEE Press, 2010: 726-733. DOI:10.1109/IROS.2010.5652781. |
| [4] | BOUTIN L, EON A, ZEGHLOUL S, et al. From human motion capture to humanoid locomotion imitation application to the robots HRP-2 and HOAP-3[J]. Robotica, 2011, 29 (2) : 325-334. DOI: 10.1017/S0263574710000172 |
| [5] | LIU H Y, WANG W J. Image recognition and force measurement application in the humanoid robot Imitation[C]//Proc IEEE Transactions on Instrumentation and Measurement. Piscataway: IEEE Press, 2012: 149-161. DOI:10.1109/TIM.2011.2161025. |
| [6] | YI S J, MCGILL S G, ZHANG B T, et al. Active stabilization of a humanoid robot for real-time imitation of a human operator[C]//Proc 12th IEEE-RAS Conf on Humanoid Robots. Piscataway: IEEE Press, 2012: 761-766. DOI:10.1109/HUMANOIDS.2012.6651605. |
| [7] | VUGA R, OGRINC M, GAMS A, et al. Motion capture and reinforcement learning of dynamically stable humanoid movement primitives[C]//Proc 2013 IEEE Conf on Robotics and Automation. Piscataway: IEEE Press, 2013: 5284-5290. DOI:10.1109/ICRA.2013.6631333. |
| [8] | MUNIRATHINAM K, CHEVALLEREAU C, SAKKA S. Offline imitation of a human motion by a humanoid robot under balance constraint[J]. Mechanisms and Machine Science, 2014, 20 : 269-282. DOI: 10.1007/978-3-319-05431-5_18 |
| [9] | MIURA K, MORISAWA M, NAKAOKA S et al. Robot motion remix based on motion capture data towards human-like locomotion of humanoid robots[C]//Proc IEEE-RAS Conf on Humanoid Robots. Piscataway: IEEE Press, 2009: 7-10. DOI:/10.1109/ICHR.2009.5379535. |
| [10] | NAKAZAWA A, NAKAOKA S, IKEUCHI K, et al. Imitating human dance motions through motion structure analysis[C]//2002 IEEE-RSJ Conf on Intelligent Robots and Systems. Piscataway: IEEE Press, 2002: 2539-2544. DOI:10.1109/IRDS.2002.1041652. |
| [11] |
张利格, 黄强, 杨洁, 等. 仿人机器人复杂动态动作设计及相似性研究[J].
自动化学报, 2007, 33 (5) : 522-528.
ZHANG Lige, HUANG Qiang, YANG Jie, et al. Design of humanoid complicated dynamic motion with similarity considered[J]. Acta Automatica Sinica, 2007, 33 (5) : 522-528. |
| [12] | MATARIC M J. Getting humanoids to move and imitate[J]. Intelligent Systems, 2000, 15 (4) : 18-24. DOI: 10.1109/5254.867908 |
| [13] | BENTIVEGNA D C, ATKESON C G. Learning similar tasks from observation and practice[C]// Proc IEEE-RSJ Conf on Intelligent Robots and Systems. Piscataway: IEEE Press, 2006: 4994-5000. DOI:10.1109/IROS.2006.281989. |
| [14] | TAKANO W, YAMANE K, YAMAMOTO S K, et al. Primitive communication based on motion recognition and generation with hierarchical mimesis model[C]//Proc of the IEEE Conf on Robotics and Automation. Piscataway: IEEE Press, 2006: 3602-3609.DOI:10.1109/ROBOT.2006.1642252. |
| [15] | LEE D, KUNORI H, NAKAMURA Y. Association of whole body motion from tool knowledge for humanoid robots[C]//Proc IEEE-RSJ International Conf on Intelligent Robots and Systems. Piscataway: IEEE Press, 2008: 2867-2874. DOI:10.1109/IROS.2008.4650611. |
| [16] | CHRISTOPHER S C, ANTON B, EDWARD R. Teleoperation of a humanoid robot using full-body motion capture, example movements, and machine learning[C]//Proc 2012 Australasian Conf on Robotics and Automation. Piscataway: IEEE Press, 2012: 1969-2016. |
| [17] | HWANG C L, CHEN B L, SYU H T, et al. Humanoid robot’s visual imitation of 3-D motion of a human subject using neural-network-based inverse kinematics[J]. IEEE Systems Journal, 2016, 10 (2) : 685-696. DOI: 10.1109/JSYST.2014.2343236 |
| [18] | REMPIS C W. A neural network to capture demonstrated motions on a humanoid robot to rapidly create complex central pattern generators as reusable neural building blocks[C]//Proc of the 2013 IEEE Conf on Robotics and Automation. Piscataway: IEEE Press, 2013: 5291-5296. DOI:0.1109-ICRA.2013.6631334. |
| [19] |
赵晓军, 黄强, 彭朝琴, 等. 基于人体运动的仿人型机器人动作的运动学匹配[J].
机器人, 2005, 27 (4) : 358-361.
ZHAO Xiaojun, HUANG Qiang, PENG Zhaoqin, et al. Kinematics mapping of humanoid motion based on human motion[J]. Robot, 2005, 27 (4) : 358-361. |
| [20] |
柯文德. 基于人体运动相似性的仿人机器人运动规划关键技术研究[D]. 哈尔滨:哈尔滨工业大学,2013.
KE Wende. Research on key technologies of motion planning humanoid robot based on similarity locomotion of human actor[D]. Harbin: Harbin Institute of Technology, 2013. |
| [21] |
彭伟. 基于人体运动捕获数据的运动编辑技术研究与实现[D]. 长沙:湖南大学,2012.
PENG Wei. The research and implementation on motion edit technology based on human motion capture data[D]. Changsha: Hunan University, 2012. |
| [22] | KOVAR L, GLEICHER M, PIGHIN F. Motion graphs[C]// Proc 29 Annual Conf on Computer Graphics and Interactive Techniques. Piscataway: IEEE Press, 2002: 473-482. DOI:10.1109/TVCG.2012.149. |
 2017, Vol. 49
2017, Vol. 49


