电主轴作为高速数控机床的核心部件,其静态特性和动态特性直接影响机械加工的精度、加工表面的质量和机床的可靠性、稳定性[1-3]. 当电主轴的工作频率接近电主轴的固有频率,产生共振现象,最终导致电主轴甚至整个机床破坏;共振产生的噪声还会危害操作者的健康[4-5]. 所以,有必要对电主轴进行动力学分析,并研究其频率可靠性. 张德龙[6]采用点估计方法对电主轴静刚度进行了可靠性灵敏度分析,但点估计方法不适合解决一些相关变量的可靠性问题;何雪浤等[7]应用响应面法研究了电主轴刚度可靠性,但是只考虑了几何参数对可靠度的影响;蒋彦收[8]利用Ansys/PDS模块采用Monte-Carlo方法研究了电主轴的抗共振可靠性和敏感参数,但是Monte-Carlo方法需要在样本量非常大时得到精确解,不仅计算量大,而且非常耗时.
本文采用ANSYS软件建立了电主轴系统的参数化模型;由Block Lanczos模态分析方法提取了系统前5阶的固有频率及振型;考虑到电主轴几何参数和材料参数的变化会引起电主轴固有频率的改变,进而导致电主轴工作时发生共振,需要对电主轴的频率可靠度进行计算,将ISIGHT软件和ANSYS软件多次集成,先对随机变量筛选,再以BP神经网络拟合出电主轴低阶固有频率与各变量的函数关系,建立关于低阶固有频率与临界频率的极限状态方程;采用改进一次二阶矩方法对电主轴频率可靠性灵敏度进行了分析.
1 电主轴的结构分析及简化一般情况下,电主轴系统是将电机与机床主轴设计为一体,构成无外壳电机. 空心转子装配在机床的主轴上,使得机床主轴成为电机转子;同时,定子装配在主轴单元的壳体内部,使壳体成为电机座,内装式电动机直接驱动机床主轴[9].
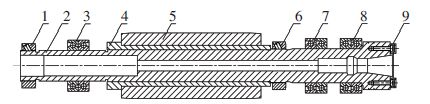
电主轴中的壳体、定子、外围部件对系统工作时的共振特性影响不大,在分析时可以忽略,而只考虑旋转组件,如主轴、电机转子、锁紧螺母等,见图 1.
|
1、6—锁紧螺母;2—主轴;3—后轴承组;4—过盈套筒;5—电机转子;7—1号前轴承组;8—2号前轴承组;9—平键 图 1 旋转组件 Figure 1 Rotary components |
本文研究的电主轴的主轴为阶梯轴,内部中空,电机转子通过过盈套筒安装在主轴上. 电主轴由三组角接触陶瓷球轴承支承,前轴承有两组,每组由两列轴承串联安装,后轴承有一组轴承.
为方便参数化建模,更准确地分析电主轴的实际情况,对主轴单元和轴承单元进行以下简化:
1) 在主轴达到最高转速时,电机转子与过盈套筒、过盈套筒与轴体之间仍旧是过盈配合形式,将三者等效为同密度的材料,进行一体化处理. 同时,对主轴前端通过螺钉与轴体结合在一起的平键以及前后轴承锁紧螺母,也作同样处理; 2)忽略局部细节特征,如倒角、小孔、螺纹、退刀槽及变化不太大的阶梯轴等; 3)将阶梯度不大主轴的内孔简化成孔径相同的当量内孔,并将主轴前端的内部锥孔作直孔处理.
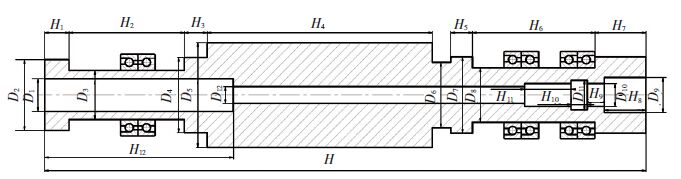
简化后的主轴单元结构如图 2所示,同时也需要对轴承单元进行以下简化:
|
图 2 主轴单元结构简图 Figure 2 Simplified spindle system structure |
1) 前后轴承简化成径向可压缩的弹簧单元,弹性支承的支点在主轴轴线与轴承接触线的交点处,见图 3;2)认为所有轴承都没有角刚度,仅有径向刚度,并视刚度为一定的常数;忽略轴承的转速及荷载对刚度的影响.

|
图 3 轴承简化模型 Figure 3 Simplified bearing mode |
前后轴承为FAG公司超精密高速主轴轴承,型号分别为XCB7010.E.T.P4S、XCB7009.E.T.P4S,采用轻预紧方式,接触角均为25°. 轴承的径向刚度K(N/m)按公式(1)[10]计算:
| $\begin{align} & K=1.772\text{ }36\times {{10}^{7}}{{K}_{\text{m}}}{{\left( {{Z}^{2}}{{D}_{\text{b}}} \right)}^{1/3}}\cdot \\ & {{\cos }^{2}}\alpha /({{\sin }^{1/3}}\alpha ){{({{F}_{\text{a}0}})}^{1/3}}. \\ \end{align}$ | (1) |
式中:Z为滚动体数目;Db为滚动体直径(m);α为接触角(°);Fa0为轴向预紧力(N);Km为材料修正系数,陶瓷球轴承取1.3.
经计算,前后轴承的径向刚度分别为:Ks=201.84×106 N/m,Kt=185.17×106N/m. 轴承径向方向,可以视作并联弹簧系统,轴承刚度的一半即是相应系统每个弹簧的刚度.
2 电主轴的模态分析 2.1 模态分析的运动方程由达朗贝尔原理,可以建立多自由度的动力学基本方程:
| $M\ddot{q}\left( t \right)+C\dot{q}\left( t \right)+Gq\left( t \right)=F\left( t \right).$ |
式中:M为质量矩阵,C为阻尼矩阵,G为刚度矩阵,$\ddot{q}\left( t \right)$为加速度列向量,$\dot{q}\left( t \right)$为速度列向量,q(t)为节点位移列向量,F(t)为激振力列向量.
由于一般电主轴结构的阻尼较小,研究中忽略阻尼对电主轴固有频率和振型的影响. 当F(t)=0,C=0时,便可得到主轴系统的无阻尼自由运动微分方程:
| $M\ddot{q}\left( t \right)+Gq\left( t \right)=0.$ | (2) |
设解为
| $q=\varphi \sin ({{\lambda }_{0}}t+\theta ).$ | (3) |
式中: φ为振幅列矩阵,λ0为系统的固有频率,θ为初相位. 式(3)带入式(2),有
| $(G-{{\omega }^{2}}M)\varphi =0.$ | (4) |
求解式(4)的特征值和特征向量,即求得电主轴的固有频率与振型.
2.2 电主轴参数化模型的建立为使仿真模型更加准确,在有限元分析软件ANSYS中直接进行参数化建模. 主轴材料为20 CrMnTi,弹性模量Em=2.12×1011 N/m2,密度Dm=7 860 kg/m3,泊松比Pm=0.289. 主轴选用SOLID185实体单元,轴承采用COMBINE14弹簧单元.
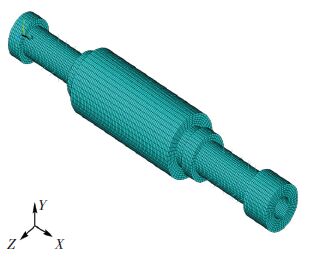
首先,建立主轴的旋转截面,把不规则的图形分割成多个四边形. 然后,借助MESH200单元对截面进行映射网格划分,由于MESH200单元只辅助网格划分,没有荷载、实常数、自由度以及材料特性,不影响模型计算结果,所以建完模型后可忽略此单元. 沿中心轴线旋转即可以生成三维实体模型,同时生成体网格. 这样划分的网格有规律,单元数量少,分析也较准确. 建立弹簧单元,图 4为最终的电主轴参数化有限元分析模型,该模型共有67 029个单元和74 736个节点.
|
图 4 电主轴有限元分析模型 Figure 4 FEA model of the motorized spindle |
根据电主轴的工作情况添加以下边界条件:前端轴承限制主轴的轴向位移,要对每个前轴承的内部4个节点(P1、P2、P3、
电主轴系统的振动可以看作各阶振型的线性叠加,而主轴系统的动态特性主要取决于低阶振型,所以分析电主轴的振动特性时,通常提取前5~10阶模态参数. 本文在动力学模型的基础上,选用Block Lanczos模态提取法,得到了前5阶固有频率和振型.
电主轴的频率和转速的关系为
| $\eta =60\lambda .$ |
其中:η为转速(r/min),λ为频率(Hz).
电主轴共振时的转速称为临界转速,各阶振型与对应的临界转速如表 1.
| 表 1 电主轴的前5阶固有频率、对应振型和临界转速 Table 1 The first five natural frequencies,vibration modes and critical speeds of motorized spindle |
由于没有限制主轴的轴向转动自由度,所以主轴的第1阶模态为电主轴的转动,频率为零. 第2阶、第3阶固有频率相等,为式(4)的一对重根,是电主轴的最低固有频率,其振型都为一阶弯曲. 此时,电主轴的临界转速为47 650.20 r/min,对于4、5阶也如此.
通常电主轴工作时最高转速要小于其最低临界转速的75%. 本文电主轴的最高转速为33 000 r/min,<35 737.65 r/min,可以认为电主轴模型是合理的. 在电主轴的设计制造过程中,尺寸参数和材料参数会有一定的变动,而较小的变化也会使电主轴的固有频率发生很大的变化;同时,33 000 r/min 与35 737.65 r/min相差不是很大,在实际工作时电主轴发生共振的机率会增加,因此有必要对电主轴的频率可靠度进行计算,并分析出可靠性敏感的参数.
3 电主轴频率可靠度的功能函数的拟合 3.1 基于ISIGHT随机变量的筛选和样本数据库的构建电主轴的结构设计尺寸数目较多,而部分尺寸参数的变化对电主轴的频率可靠性影响不明显,所以在计算可靠度时可以忽略这些参数. ISIGHT软件提供了实验设计(DOE)的优化算法,可以控制多变量参数,对实验过程进行实时监控[11-12]. 利用ISIGHT软件集成ANSYS,选取主要设计参数H、H1、H2、H5~H12以及R1、R3、R8、R10~R12,采用优化的拉丁方方法进行DOE实验设计. 本文中各随机参数服从正态分布,随机变量的标准差和均值的关系为
| ${{\sigma }_{x}}=z\cdot {{\mu }_{x}}.$ |
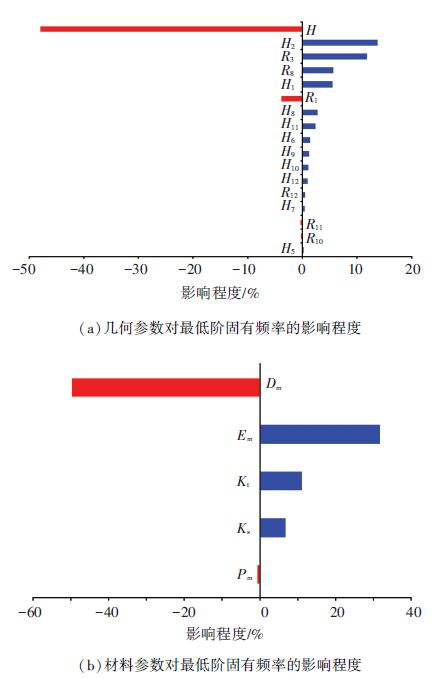
式中:σx为标准差,μx为均值,z为变差系数. 若无试验数据,可根据公差标准确定几何参数的变差系数,一般将公称尺寸的0.001 5倍作为设计公差,若公差水平由3σ原则确定,则z取0.00 5;对于材料参数,z取0.05[13-14]. 以μx±σx原则设定各变量的上下限,抽取300组样本,分析Pareto贡献率图 5(a),确定影响固有频率的主要尺寸参数有H、H2、R3,其中,H2和R3对最低固有频率是正影响,H对最低固有频率是负影响. 同理,将材料参数:密度Dm、弹性模量Em、泊松比Pm、前轴承的刚度Ks以及后轴承的刚度K
|
图 5 Pareto贡献率图 Figure 5 Pareto plot of the parameters |
BP神经网络输入层参数是上文提到的6个变量,输出层参数为电主轴系统最低固有频率. 通常,若隐含层节点数足够多,并且隐含层采用Sigmoid函数,一个隐含层就可以使神经网络以任意精度逼近所需函数[15]. 因此本文只采用一个隐含层,BP神经网络输入层的节点数为6,输出层节点数为1. 隐含层节点数的初始值可通过如下经验公式[16]估计:
| $Q=\sqrt{G+L}+s.$ |
式中:Q为隐含层的节点数,G和L分别为输入层与输出层节点数,s为1~10之间的整数. 以提高训练精度、减小拟合误差、缩短训练时间、避免出现“过拟合”现象为原则,采用试凑法进行多次拟合实验,最终选取Q=27.
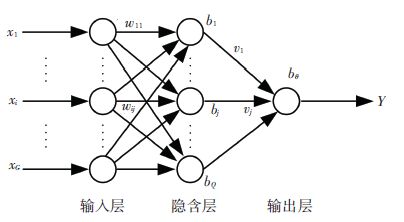
BP神经网络的结构见图 6,最低固有频率Y与随机变量X之间的函数关系可表示为
| $Y=F\left( X \right)=\psi ({{b}_{\theta }}+\sum\limits_{j=1}^{Q}{{{v}_{j}}\varphi }({{b}_{j}}+\sum\limits_{i=1}^{G}{{{w}_{ij}}{{x}_{i}}})).$ |
|
图 6 BP神经网络结构 Figure 6 Structure of BP networks |
式中:wij为输入层到隐含层的网络连接权值;vi为隐含到输出层的网络连接权值;bj为隐含层的阈值;bθ为输出层的阈值;φ(·)为隐含层的传递函数,本文选用Sigmoid函数;ψ(·)为输出层的传递函数,选用Purelin线性函数.
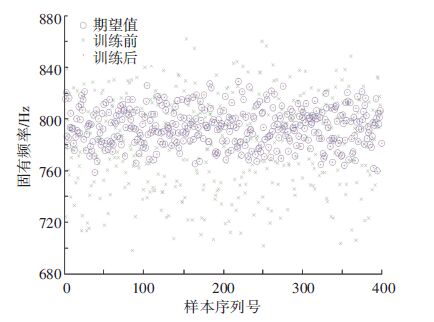
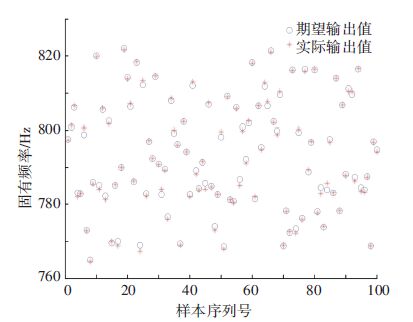
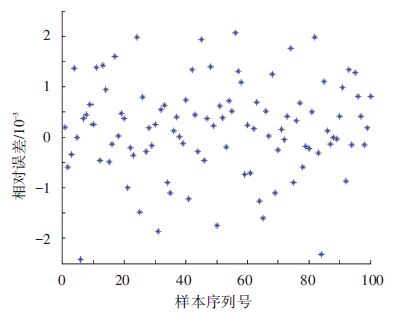
将3.1节收集到的500组数据随机划分成400组训练样本和100组测试样本,先进行函数拟合,后进行测试. 训练过程曲线如图 7 所示,在第1 000次训练后样本的均方误差达到了9.999 7×10-6;从图 8可以看到,训练后网络实际输出接近期望输出,误差较小,网络拟合效果较理想,训练出的函数精度较高;图 9反映了测试过程期望输出数据和实际输出数据的对比,由误差图 10可知,测试数据相对误差也很小. 因此,拟合出来的函数可以用于构建功能函数,进而计算电主轴的可靠度以及可靠性灵敏度.

|
图 7 神经网络训练过程误差变化 Figure 7 Change of error to achieve the target precision value in training phase |
|
图 8 训练阶段期望值和响应值的对比 Figure 8 Contrast between the expected data and actual output data in training phase |
|
图 9 测试阶段期望输出值和实际输出值的对比 Figure 9 Contrast between the expected data and actual output data in testing phase |
|
图 10 测试误差的分布 Figure 10 Distribution of the testing errors |
设结构的极限状态函数,即功能函数为
| $g\left( X \right)=g({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{i}},\cdots {{x}_{n}}).$ |
式中:$X={{({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}})}^{\text{T}}}$是影响功能的相互独立的基本随机变量,n为随机变量的数目. 当g(X)>0时,结构可靠;当g(X)<0,结构失效;当g(X)=0时结构处在极限状态下,且将g(X)=0称为极限状态方程. 通常,功能函数可定义为响应量与阈值的差,即
| $g\left( X \right)=r\left( X \right)-{{r}^{*}}.$ |
式中r(X)为响应量,用来描述位移、应力、振动特征量等系统行为特征. 因电主轴的最高转速为33 000 r/min,对应频率为550 Hz,即阈值r*=550,则功能函数可以表示成
| $g\left( X \right)=r\left( X \right)-550=0.75F\left( X \right)-550.$ | (5) |
此函数为非线性函数,可靠性指标β可以表示为
| $\beta ={{\mu }_{g(X)}}/{{\sigma }_{g(X)}}.$ |
其中μg(X)、σg(X)分别为函数(5)的均值和标准差.
若随机变量服从正态分布,可靠度R可表示为
| $R={{P}_{\text{r}}}=1-{{P}_{\text{f}}}=\Phi \left( \beta \right).$ |
式中:Pr为可靠概率,Pf为失效概率,Φ(·)为标准正态分布函数.
改进的一次二阶矩方法(AFOSM)[17]与一次二阶矩方法(FOSM法)相似,都是将功能函数线性展开求可靠度. 当功能函数非线性程度较高时,FOSM法得到的解精度不高,有时甚至是错误的. 而AFOSM法将失效域中最可能失效点(设计点)作为展开点,又能考虑随机变量分布的实际情况,适合求解非线性功能函数问题.
若设计点为${{X}^{*}}={{({{x}_{1}}^{*},{{x}_{2}}^{*},\cdots ,{{x}_{n}}^{*})}^{\text{T}}}$,将功能函数以Taylor公式展开后,可得
| $\begin{align} & {{\mu }_{g(X)}}\approx g({{X}^{*}})+\sum\limits_{i=1}^{n}{\frac{\partial g({{X}^{*}})}{{{x}_{i}}({{\mu }_{{{x}_{i}}}}-x_{i}^{*})}}, \\ & \sigma _{g(X)}^{2}\approx \sum\limits_{i=1}^{n}{{{[\partial g({{X}^{*}})/\partial {{x}_{i}}]}^{2}}}\sigma _{{{x}_{i}}}^{2}, \\ & \beta =\frac{g({{X}^{*}})+\sum\limits_{i=1}^{n}{\frac{\partial g({{X}^{*}})}{\partial {{x}_{i}}}}({{\mu }_{{{x}_{i}}}}-x_{i}^{*})}{\sqrt{{{\sum\limits_{i=1}^{n}{\left[ \frac{\partial g({{X}^{*}})}{\partial x_{i}^{2}} \right]}}^{2}}\sigma _{{{x}_{i}}}^{2}}}. \\ \end{align}$ |
可靠度RAF对相互独立随机变量的可靠性灵敏度表达式分别为
| $\begin{align} & \frac{\partial {{R}_{\text{AF}}}}{\partial {{\mu }_{{{x}_{i}}}}}=-\frac{\partial {{P}_{\text{f}}}}{\partial {{\beta }_{\text{AF}}}}\frac{\partial {{\beta }_{\text{AF}}}}{\partial {{\mu }_{{{x}_{i}}}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{g(X)}}}\cdot \\ & \exp \left[ -0.5{{\left( {{\mu }_{g(X)}}/{{\sigma }_{g(X)}} \right)}^{2}} \right]\cdot \partial g\left( {{X}^{*}} \right)/\partial {{x}_{i}}, \\ & \frac{\partial {{R}_{\text{AF}}}}{\partial {{\sigma }_{{{x}_{i}}}}}=-\frac{\partial {{P}_{\text{f}}}}{\partial {{\beta }_{\text{AF}}}}\frac{\partial {{\beta }_{\text{AF}}}}{\partial {{\sigma }_{{{x}_{i}}}}}=-\frac{{{\mu }_{g(X)}}{{\sigma }_{{{x}_{i}}}}}{\sqrt{2\pi }\sigma _{g\left( X \right)}^{3}}\cdot \\ & \exp \left[ -0.5{{\left( {{\mu }_{g(X)}}/{{\sigma }_{g(X)}} \right)}^{2}} \right]\cdot {{\left( \partial g\left( {{X}^{*}} \right)/\partial {{x}_{i}} \right)}^{2}}. \\ \end{align}$ |
对应的量纲一的灵敏度可由式(6)、(7)计算:
| ${{S}_{{{\mu }_{{{x}_{i}}}}}}=\partial {{R}_{\text{AF}}}/\partial {{\mu }_{{{x}_{i}}}}\cdot ({{\sigma }_{{{x}_{i}}}}/{{R}_{\text{AF}}}),$ | (6) |
| ${{S}_{{{\sigma }_{{{x}_{i}}}}}}=\partial {{R}_{\text{AF}}}/\partial {{\sigma }_{{{x}_{i}}}}\cdot ({{\sigma }_{{{x}_{i}}}}/{{R}_{\text{AF}}}).$ | (7) |
采用Monte-Carlo计算结构可靠度的基本思想是:建立随机变量X的联合概率密度分布函数${{f}_{{\tilde{X}}}}\left( X \right)={{f}_{{\tilde{X}}}}({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}})$,之后抽取大量随机样本Xτ(τ=1,2,…,N),分别计算功能函数值g(Xτ),然后统计g(Xτ)≤0的样本数Nf,则失效概率的估计值为
| ${{{\hat{P}}}_{\text{f}}}={{N}_{\text{f}}}/N.$ |
设失效域T={X|g(X)≤0},失效域指示函数为IT(X),当X∈T时,IT(X)=1;反之,IT(X)=0. E[·]为数学期望函数,RMC为可靠度. 对于相互独立的正态分布随机变量,均值和标准差的可靠性灵敏度表示成
| $\begin{align} & \frac{\partial {{R}_{\text{MC}}}}{\partial {{\mu }_{{{x}_{i}}}}}=-E\left[ \frac{{{I}_{T}}\left( X \right)}{{{f}_{{\tilde{X}}}}\left( X \right)}\frac{\partial {{f}_{{\tilde{X}}}}\left( X \right)}{\partial {{\mu }_{{{x}_{i}}}}} \right]= \\ & \frac{1}{N}\sum\limits_{\tau =1}^{N}{{{I}_{T}}({{X}_{\tau }})({{\mu }_{{{x}_{i}}}}-{{x}_{i}})/\sigma _{{{x}_{i}}}^{2}}, \\ & \frac{\partial {{R}_{\text{MC}}}}{\partial {{\sigma }_{{{x}_{i}}}}}=-E\left[ \frac{{{I}_{T}}\left( X \right)}{{{f}_{{\tilde{X}}}}\left( X \right)}\frac{\partial {{f}_{{\tilde{X}}}}\left( X \right)}{\partial {{\sigma }_{{{x}_{i}}}}} \right]= \\ & \frac{1}{N}\sum\limits_{\tau =1}^{N}{{{I}_{T}}({{X}_{\tau }})}\frac{1}{{{\sigma }_{{{x}_{i}}}}}[1-{{(({{x}_{i}}-{{\mu }_{{{x}_{i}}}})/{{\sigma }_{{{x}_{i}}}})}^{2}}]. \\ \end{align}$ |
对应的量纲一的灵敏度可由式(8)、(9)计算:
| ${{S}_{{{\mu }_{{{x}_{i}}}}}}=\partial {{R}_{\text{MC}}}/\partial {{\mu }_{{{x}_{i}}}}\cdot ({{\sigma }_{{{x}_{i}}}}/{{R}_{\text{MC}}}),$ | (8) |
| ${{S}_{{{\sigma }_{{{x}_{i}}}}}}=\partial {{R}_{\text{MC}}}/\partial {{\sigma }_{{{x}_{i}}}}\cdot ({{\sigma }_{{{x}_{i}}}}/{{R}_{\text{MC}}}).$ | (9) |
本文随机变量$X=[{{x}_{1}},\cdots ,{{x}_{i}},\cdots ,{{x}_{6}}\left] = \right[{{D}_{\text{m}}},{{E}_{\text{m}}},H,{{H}_{2}},{{K}_{t}},{{R}_{3}}]$. 在MATLAB中,分别采用两种方法对电主轴频率可靠度及可靠性灵敏度进行计算,结果见表 2和图 11~14.
| 表 2 可靠度计算结果 Table 2 Results of reliability calculation |

|
图 11 采用AFOSM方法的量纲一的均值灵敏度 Figure 11 Dimensionless sensitivity of mean by AFOSM |
|
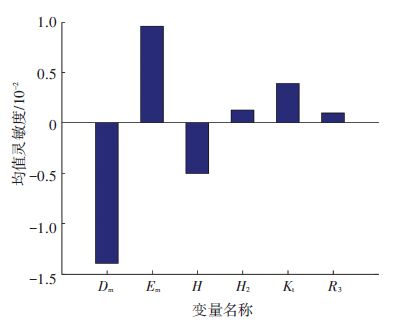
图 12 采用Monte-Carlo方法的量纲一的均值灵敏度 Figure 12 Dimensionless sensitivity of mean by MCS |
|
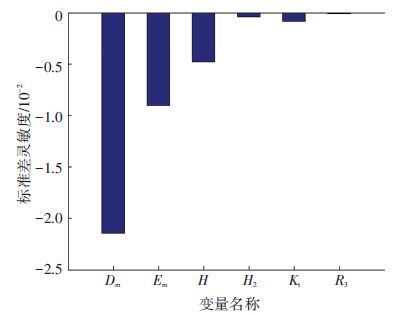
图 13 采用AFOSM方法的量纲一的标准差灵敏度 Figure 13 Dimensionless sensitivity of standard deviation by AFOSM |
|
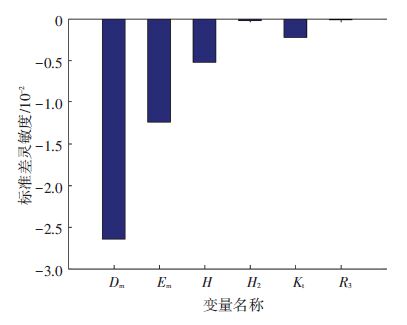
图 14 采用Monte-Carlo方法的量纲一的标准差灵敏度 Figure 14 Dimensionless sensitivity of standard deviation by MCS |
从表 2中的可靠度指标β值可以看出,改进一次二阶矩方法计算出的可靠度和Monte-Carlo方法计算的结果很接近,说明改进一次二阶矩方法计算的结果较准确,且系统是可靠的.
由图 11、图 13可知,Dm、Em、H的均值和标准差对可靠度影响较显著;Em、H2、Kt、R3均值的增加和Dm、H均值的减少均会使电主轴系统趋于可靠;6个变量参数标准差的增加都会使电主轴系统趋于不可靠;在所有变量参数中,Dm的均值和标准差影响最大,Em次之,R3的影响最小.
对比两种方法计算的灵敏度结果可知,相同参数对可靠度的影响程度和影响性质基本一致. 因此,由改进一次二阶矩方法计算的可靠性灵敏度结果正确,同时再次验证了神经网络拟合的函数较合理.
在电主轴设计制造过程中要严格控制可靠度敏感的参数Dm、Em,保证电主轴总长度 的加工精度;可适当调整相应值,进行电主轴的参数优化,以改善电主轴的性能.
5 结 论1) 本文基于有限元法对电主轴参数化建模后进行模态分析,由结果可知,电主轴工作时最高转速与其最低临界转速的75%相差不大. 当电主轴的几何参数和材料参数变化时,电主轴共振的可能性增加,因而对影响电主轴共振特性的参数进行了可靠性分析.
2) 将ISIGHT软件和ANSYS软件集成,采用优化的拉丁方方法进行实验设计,建立了电主轴最低固有频率与系统随机变量的数据库. 采用泛化能力较好的BP神经网络,拟合了对应的函数关系,并以此构建出了电主轴频率的功能函数.
3) 采用改进一次二阶矩方法计算了电主轴频率可靠度和可靠性灵敏度,并使用Monte-Carlo方法验证了计算结果的正确性. 因Monte-Carlo方法需要在样本量非常大时才能得到精确解,不仅计算量大,而且非常耗时; 而改进一次二阶矩方法避免了其局限性,提高了分析效率.
4) 根据可靠性灵敏度的计算结果,分析了各随机变量的均值与标准差对电主轴系统频率可靠度的影响情况,对电主轴优化设计和改善电主轴性能具有一定的指导意义.
| [1] | ABELE E, ALTINTAS Y, BRECHER C. Machine tool spindle units[J]. CIRP Annals-Manufacturing Technology, 2010, 59 (2) : 781-802. DOI: 10.1016/j.cirp.2010.05.002 |
| [2] | LIU D, ZHANG H, TAO Z, et al. Finite element analysis of high-speed motorized spindle based on ANSYS[J]. Open Mechanical Engineering Journal, 2011, 5 (1) : 1-10. DOI: 10.2174/1874155X01105010001 |
| [3] | MAEDA O, CAO Y, ALTINTAS Y. Expert spindle design system[J]. International Journal of Machine Tools and Manufacture, 2005, 45 (4) : 537-548. DOI: 10.1016/j.ijmachtools.2004.08.021 |
| [4] | 张义民. 机械振动学漫谈[M]. 北京: 科学出版社, 2010 : 57 -67. |
| [5] |
田华. 数控机床高速电主轴结构设计及性能分析[D]. 成都:四川大学, 2006 DOI:10.7666/d.y993861.
TIAN Hua. The construction design and general performance analysis of high-speed motorized spindle which used in NC machine[D]. Chengdu: Sichuan University, 2006. DOI:10.7666/d.y993861. |
| [6] |
张德龙. 基于点估计的电主轴可靠性灵敏度分析和可靠性稳健设计[D]. 沈阳: 东北大学, 2010.
ZHANG Delong. Reliability sensitivity analysis and reliability robust design of electric spindle based on point estimation[D]. Shenyang: Northeastern University, 2010. |
| [7] | 何雪浤, 蒋彦收, 朱孟兵. 基于响应面法的高速电主轴刚度可靠性分析[C]//2011年全国机械行业可靠性技术学术交流会暨第四届可靠性工程分会第三次全体委员大会论文集. 大同: 中国机械工程学, 2011. |
| [8] |
蒋彦收. 高速电主轴可靠性分析与研究[D]. 沈阳: 东北大学,2011 DOI:10.7666/d.J0124055.
JIANG Yanshou. Research and analysis of reliability for high-speed motorized spindle[D]. Shenyang: Northeastern University, 2011. DOI:10.7666/d.J0124055. |
| [9] |
张伯霖, 张志润, 肖曙红. 超高速加工与机床的零传动[J].
中国机械工程, 1996, 7 (5) : 37-41.
ZHANG Bolin, ZHANG Zhirun, XIAO Shuhong. Ultra-high speed machining and zero transmission of machine tools[J]. China Mechanical Engineering,, 1996, 7 (5) : 37-41. |
| [10] | 戴曙. 机床滚动轴承应用手册[M]. 北京: 机械工业出版社, 1993 : 150 -219. |
| [11] | LIAO H, FAN J, WANG R, et al. Multidisciplinary optimization technology research on typical turbine assembly structure[C]//ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal: American Society of Mechanical Engineers, 2014: V001T01A012. DOI:10.1115/IMECE2014-37473. |
| [12] |
陈辰, 段富海. 基于 ANSYS 和 ISIGHT 的 EHA 作动筒结构分析与优化[J].
机电工程技术, 2014 (4) : 80-84.
CHEN Chen, DUAN Fuhai. Structural analysis and optimization of the action cylinder of EHA based on ANSYS and ISIGHT[J]. Mechanical & Electrical Engineering technology, 2014 (4) : 80-84. DOI: 10.3969/j.issn.1009-9492.2014.04.022 |
| [13] | 张义民. 汽车零部件可靠性设计[M]. 北京: 北京理工大学出版社, 2000 : 138 -141. |
| [14] |
王洪建. 基于NSGA-Ⅱ的变速器齿轮系多目标可靠性优化设计[D]. 武汉: 武汉理工大学, 2010 DOI:10.7666/d.y1680971.
WANG Hongjian. Multi-objective reliability optimal design of transmission gear train based on NSGA-Ⅱ[D]. Wuhan: Wuhan University of Technology, 2010. DOI:10.7666/d.y1680971. |
| [15] | CYBENKO G. Approximation by superpositions of a sigmoidal function[J]. Mathematics of control, signals and systems, 1989, 2 (4) : 303-314. DOI: 10.1007/BF02551274 |
| [16] | 傅荟璇, 赵红. MATLAB 神经网络应用设计[M]. 北京: 机械工业出版社, 2010 : 83 -97. |
| [17] | 赵国藩, 金伟良, 贡金鑫. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000 : 21 -52. |
 2017, Vol. 49
2017, Vol. 49


