并联机器人由于具有高精度、高刚度及大负载自重比等优点,得到了广泛关注,并已大量应用于高速搬运、运动模拟与电子制造等行业中[1]. 为了降低成本并减小能耗,本体轻量化设计将是必然选择. 然而,在高速或重载运行场合,轻量化的机械本体将会产生明显的弹性变形及振动,因而机器人末端运动由刚体运动及弹性变形与振动产生的弹性位移组成. 采用传统针对刚体机器人的控制方法将无法保证柔性机器人末端良好的跟踪精度.
Dwivedy等[2]对含柔性杆件机器人动力学建模进行了综述. 由于杆件柔性的存在,当选择机器人末端作为输出时,系统将呈现非最小相位特性. 文献[3-5]将杆件弹性计及到机器人的末端位置进行输出重定义,并采用针对刚体机器人的控制算法对新输出进行控制;然而,该方法只能实现点位控制,不能保证对末端轨迹的跟踪控制[6]. 奇异摄动是另外一种解决含弹性环节机器人非最小相位特性的有效方法,通过引入小参数对刚柔耦合模型进行降阶,将其分解为快慢两个子系统,并采用复合控制算法设计两个子系统控制器,实现了对刚体运动的控制及弹性振动的快速抑制;然而,随着变形量的加大,奇异摄动算法显现出了不足,同时该算法无法实现对弹性位移的补偿[7-9]. Khorasani[10]通过对快速子系统变量的高阶逼近,提出了积分流形方法,使得振动抑制效果有了较大提高. 通过将弹性位移引入机器人末端,并以此设计校正力矩,MOALLEM等[11]实现了两自由度串联机器人的轨迹跟踪精确控制与振动抑制. 在此基础上,Fotouhi等[12-16]通过简化校正力矩的选择,研究了柔性关节机器人、单杆柔性机器人、刚柔混合杆件机器人、两杆柔性机器人轨迹跟踪控制,并取得了良好效果.
由于闭链结构的存在,考虑杆件柔性时并联机器人模型较复杂,对其进行振动抑制与轨迹跟踪控制的研究极为有限.
为解决高速并联机器人因杆件柔性产生的弹性变形与振动问题,提高跟踪精度与动态性能,本文将以前期研究的3RRR并联机器人刚柔耦合模型为基础[17],基于小变形假设及速度映射关系描述动平台弹性位移,通过积分流形将高阶刚柔耦合模型转化为快慢两个子系统,提出基于滑模变结构控制与反演控制相结合的复合控制算法,引入高增益观测器解决曲率变化率难于测量的问题,并开展仿真研究,对算法可行性进行验证.
1 3RRR并联机器人动力学模型图 1为本文采用的3RRR并联机器人,由3个支链组成,每个支链由一个主动杆和一个被动杆组成,末端为动平台. 图 2中O-XY与G-xGyG为固结在基座与动平台的两个坐标系. 其中θi与βi分别为主动杆与被动杆的转角,i=1,2,3,动平台末端位姿在基坐标系下的描述为$\eta ={{\left[ \begin{matrix} x & y & \varphi \\ \end{matrix} \right]}^{\text{T}}}$.

|
图 1 3RRR并联机器人 Figure 1 3RRR parallel manipulator |

|
图 2 3RRR并联机器人坐标系 Figure 2 Coordinates of the 3RRR parallel manipulator |
由文献[17]可知,被动杆柔性可忽略,这里只考虑主动杆变形,可以表述为
| ${{\delta }_{i}}=\sum\limits_{k=1}^{n}{\alpha _{i}^{k}m_{i}^{k}},i=1,2,3.$ |
式中:αik与mik分别为第i个主动杆的第k点处的形函数与曲率,这里取k =1.根据文献[17],当忽略被动杆并加入电机减速机的参数后,该3RRR并联机器人的动力学模型可表示为
| $\begin{align} & \left[ \begin{matrix} {{({{M}_{11}})}_{0}}+{{({{M}_{11}})}_{1}} & {{M}_{12}} \\ M_{12}^{\text{T}} & {{M}_{22}} \\ \end{matrix} \right]\left[ \begin{matrix} {\ddot{\eta }} \\ {\ddot{m}} \\ \end{matrix} \right]+\left[ \begin{matrix} 0 & 0 \\ 0 & K \\ \end{matrix} \right]\left[ \begin{matrix} \eta \\ m \\ \end{matrix} \right]+ \\ & \left[ \begin{matrix} {{\left( {{f}_{1}} \right)}_{0}}+{{M}_{{{f}_{1}}}}m+{{M}_{{{f}_{2}}}}\dot{m} \\ {{({{f}_{2}})}_{0}}+{{M}_{{{f}_{3}}}}\dot{m} \\ \end{matrix} \right]=\left[ \begin{matrix} J_{{{p}^{{{\theta }^{\tau }}}}}^{\text{T}} \\ 0 \\ \end{matrix} \right]. \\ \end{align}$ | (1) |
式中:Jm与Jg为电机与减速机转动惯量,$K=\text{diag}\left( \left[ {{k}_{\text{s}}},{{k}_{\text{s}}},{{k}_{\text{s}}} \right] \right)$为刚度矩阵,ks为杆件刚度,ig为减速比,${{({{M}_{11}})}_{0}}={{({{M}^{\prime }}_{11})}_{0}}+({{J}_{\text{m}}}+{{J}_{\text{g}}})i_{\text{g}}^{2}J_{{{p}^{\theta }}}^{\text{R}}{{J}_{p\theta }}$,τ为驱动力矩,${{({{f}_{1}})}_{0}}={{(f_{1}^{'})}_{0}}+({{J}_{\text{m}}}+{{J}_{\text{g}}})i_{\text{g}}^{2}J_{{{p}^{\theta }}}^{\text{R}}{{{\dot{J}}}_{p\theta }}\dot{\eta }$,${{(M_{11}^{'})}_{0}}$与${{(f_{1}^{'})}_{0}}$为文献[17]推导的动力学方程中质量阵与二次项中对应刚体运动部分不含m的项,(M11)1为含有m的项.
2 基于积分流形的高速并联机器人模型降阶根据动力学模型(1),定义如下状态变量[15]:
| $\left\{ \begin{align} & {{X}_{1}}=\eta ,{{X}_{2}}=\dot{\eta }; \\ & {{z}_{1}}=m/{{\varepsilon }^{2}},{{z}_{2}}=\dot{m}/\varepsilon . \\ \end{align} \right.$ | (2) |
式中:$X={{\left[ {{X}_{1}}{{X}_{2}} \right]}^{\text{T}}}$与$z={{\left[ {{z}_{1}}{{z}_{2}} \right]}^{\text{T}}}$为系统状态变量,ε∈R为大于零的小参数. 由状态变量(2)及系统方程(1),摄动形式的状态方程为
| $\left\{ \begin{align} & {{{\dot{X}}}_{1}}={{X}_{2}} \\ & {{{\dot{X}}}_{2}}={{J}_{11}}J_{p{{\theta }^{\tau }}}^{\text{T}}-{{J}_{11}}{{f}_{1}}-{{J}_{12}}{{f}_{2}}-{{J}_{12}}\tilde{k}{{z}_{1}}; \\ \end{align} \right.$ | (3) |
| $\left\{ \begin{align} & \varepsilon {{{\dot{z}}}_{1}}={{z}_{2}}, \\ & \varepsilon {{{\dot{z}}}_{2}}=J_{12}^{\text{T}}J_{p{{\theta }^{\tau }}}^{\text{T}}-J_{12}^{\text{T}}{{f}_{1}}-{{J}_{22}}{{f}_{2}}-{{J}_{22}}\tilde{k}{{z}_{1}}. \\ \end{align} \right.$ | (4) |
其中:${\tilde{k}}$为模型降阶后的刚度系数,$\tilde{k}\text{=}{{k}_{\text{s}}}{{\varepsilon }^{2}}$;J为质量阵M的逆矩阵,$J=\left[ \begin{matrix} {{J}_{11}} & {{J}_{12}}; & J_{12}^{\text{T}} & {{J}_{22}} \\ \end{matrix} \right]$.
| $\left\{ \begin{align} & z\left( {{t}^{*}},\varepsilon \right)=h{{X}_{1}}\left( {{t}^{*}},\varepsilon \right),{{X}_{2}}\left( {{t}^{*}},\varepsilon \right),\tau \left( {{t}^{*}},\varepsilon \right), \\ & \Rightarrow z\left( t,\varepsilon \right)={{h}^{a}}{{X}_{1}}\left( t,\varepsilon \right),{{X}_{2}}\left( t,\varepsilon \right),\tau \left( t \right),\varepsilon ). \\ \end{align} \right.$ | (5) |
式(5)可解释为,如果在时刻t*快速子系统变量到达积分流形轨迹,那么对于$\forall t>{{t}^{*}}$时刻,该变量将始终保持在该流形轨迹上,为了保证上述条件的成立,在原控制系统中加入附加控制变量.
ε为接近于0的小变量,积分流形h及力矩τ均为ε的函数,对上述变量进行泰勒展开得
| $\left\{ \begin{align} & h_{1}^{a}\approx {{h}_{1}}={{h}_{10}}+\varepsilon {{h}_{11}}\left( {{X}_{1}},{{X}_{2}},t \right)+\cdots +{{\varepsilon }^{p}}{{h}_{1p}}\left( {{X}_{1}},{{X}_{2}},t \right), \\ & h_{2}^{a}\approx {{h}_{2}}={{h}_{20}}+\varepsilon {{h}_{21}}\left( {{X}_{1}},{{X}_{2}},t \right)+\cdots +{{\varepsilon }^{p}}{{h}_{2p}}\left( {{X}_{1}},{{X}_{2}},t \right), \\ & \tau \approx {{\tau }_{0}}+\varepsilon {{\tau }_{1}}\left( {{X}_{1}},{{X}_{2}},t \right)+\cdots +{{\varepsilon }^{p}}{{\tau }_{p}}\left( {{X}_{1}},{{X}_{2}},t \right). \\ \end{align} \right.$ | (6) |
式中:h1与h2为h1a与h2a的逼近值,${{h}_{ij}}={{\partial }^{j}}h_{i}^{a}/(j!\partial {{\varepsilon }^{j}}){{|}_{\varepsilon }}=0$为积分流形关于小变量ε的导数,其中i=1,2; j=0,1,2,…p; p∈N+为逼近阶数. 由于杆件的弹性位移为快速子系统状态变量z的ε2倍,因此p至少取2才能将弹性位移反应到末端轨迹中,这里取p=2.
由于质量阵的逆矩阵及科氏力与离心力项均为小变量ε的函数,泰勒展开中对小参数保留到二阶,这里依然保留二阶,忽略分母中小参数,逆矩阵关于ε的泰勒级数可表示为
| $\left\{ \begin{align} & {{J}_{11}}={{({{J}_{11}})}_{0}},{{J}_{12}}={{({{J}_{12}})}_{0}}, \\ & {{J}_{22}}={{({{J}_{22}})}_{0}}+{{({{J}_{22}})}_{2}}{{\varepsilon }^{2}}/2. \\ \end{align} \right.$ | (7) |
方程(1)展开后的离心力与惯性力可表示为
| $\left\{ \begin{align} & {{f}_{1}}={{({{f}_{1}})}_{0}}+({{({{f}_{1}})}_{20}}{{h}_{10}}+{{({{f}_{1}})}_{21}}{{{\dot{h}}}_{10}}){{\varepsilon }^{2}}/2, \\ & {{f}_{2}}={{({{f}_{2}})}_{0}}+{{\varepsilon }^{2}}{{({{f}_{2}})}_{21}}{{{\dot{h}}}_{10}}/2. \\ \end{align} \right.$ | (8) |
将方程(6)~(8)代入方程(4),可得
| $\left\{ \begin{align} & {{h}_{10}}=({{J}_{22}}\tilde{k})_{0}^{-1}(J_{12}^{\text{T}}J_{p\theta }^{\text{T}}{{\tau }_{0}}-J_{12}^{\text{T}}{{({{f}_{1}})}_{0}}-{{({{J}_{22}})}_{0}}{{({{f}_{2}})}_{0}}), \\ & {{h}_{11}}=({{J}_{22}}\tilde{k})_{0}^{-1}(J_{12}^{\text{T}}J_{p\theta }^{\text{T}}{{\tau }_{1}}-{{{\dot{h}}}_{20}}), \\ & {{h}_{12}}=({{J}_{22}}\tilde{k})_{0}^{-1}(J_{12}^{\text{T}}J_{p\theta }^{\text{T}}{{\tau }_{2}}-{{{\dot{h}}}_{21}}-J_{12}^{\text{T}}({{({{f}_{1}})}_{20}}{{h}_{10}}+ \\ & {{\left( {{f}_{1}} \right)}_{21}}{{{\dot{h}}}_{10}})/2-\text{ }{{\left( {{J}_{22}} \right)}_{2}}\left( {{\left( {{f}_{2}} \right)}_{0}}+{{h}_{10}} \right)/2- \\ & {{\left( {{J}_{22}} \right)}_{0}}{{\left( {{f}_{2}} \right)}_{21}}{{{\dot{h}}}_{10}}/2) \\ & {{h}_{20}}=0,{{h}_{21}}={{{\dot{h}}}_{10}},{{h}_{22}}={{{\dot{h}}}_{11}}. \\ \end{align} \right.$ | (9) |
当不考虑杆件柔性,即小变量ε=0时,将h1带入方程(3),可得慢速子系统微分方程为
| $\left\{ \begin{align} & {{{\dot{\bar{X}}}}_{1}}={{{\dot{\bar{X}}}}_{2}} \\ & {{{\dot{\bar{X}}}}_{2}}={{({{M}_{11}})}^{-1}}_{0}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{0}}-\left( M \right)_{110}^{-1}{{({{f}_{1}})}_{0}}. \\ \end{align} \right.$ | (10) |
式(10)中X1与X2代表慢速子系统变量,为叙述方便,下文中X1与X2用X1与X2表示.
根据积分流形,快速子系统变量偏差可表示为
| $\left\{ \begin{align} & \varepsilon {{{\dot{X}}}_{{{f}_{1}}}}={{z}_{1}}-{{h}_{10}}-\varepsilon {{h}_{11}}-{{\varepsilon }^{2}}{{h}_{12}}, \\ & {{X}_{{{f}_{2}}}}={{z}_{2}}-{{h}_{20}}-\varepsilon {{h}_{21}}-{{\varepsilon }^{2}}{{h}_{22}}. \\ \end{align} \right.$ | (11) |
将式(11)乘ε,对其求导并代入方程(6),同时根据方程(9),对hij进行替代,得快速子系统方程:
| $\left\{ \begin{align} & \varepsilon {{{\dot{X}}}_{{{f}_{1}}}}={{X}_{{{f}_{2}}}}, \\ & \varepsilon {{{\dot{X}}}_{{{f}_{2}}}}=J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}\tilde{k}{{X}_{{{f}_{1}}}}-{{\varepsilon }^{2}}\left( {{\left( {{J}_{22}} \right)}_{2}}+ \right. \\ & J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{20}}{{X}_{{{f}_{1}}}}/2\varepsilon J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{21}}+ \\ & {{\left( {{J}_{22}} \right)}_{0}}{{\left( {{f}_{2}} \right)}_{21}}{{X}_{{{f}_{2}}}}/2. \\ \end{align} \right.$ | (12) |
针对慢速与快速两个子系统,设计如图 3所示的复合控制算法. 对于慢速子系统,将采用反演控制,实现对刚体末端运动的跟踪控制,同时根据速度映射关系,建立杆件弹性变形及振动量与动平台弹性位移的映射关系,根据刚体运动及弹性位移建立动平台运动表达式,并通过设计校正力矩τ1与τ2实现对弹性位移补偿. 对于快速子系统将,采用滑模控制,保证流形成立. 考虑到杆件曲率变化率难于测量,设计高增益观测器,根据曲率值对曲率变化率进行估计.

|
图 3 复合控制框图 Figure 3 Scheme of the controller |
反演控制是针对复杂非线性系统的递推控制算法,将原系统分解为不超过系统阶数的子系统,通过逐级建立各子系统Lyapunov函数来设计控制率,同时保证系统的稳定性[19]. 首先定义位置误差
| ${{e}_{1}}={{X}_{1}}-{{X}_{\text{d}}},$ |
式中Xd为指令信号,定义虚拟控制量
| ${{\upsilon }_{1}}=-{{c}_{1}}{{e}_{1}}+{{{\dot{X}}}_{\text{d}}}.$ |
其中c1为大于零的常数,同时速度误差e2可定义为
| ${{e}_{2}}={{X}_{2}}-{{\upsilon }_{1}}.$ | (13) |
根据位置误差定义Lyapunov函数
| ${{V}_{1}}=0.5e_{1}^{\text{T}}{{e}_{1}}.$ | (14) |
对式(14)求导得
| ${{{\dot{V}}}_{1}}=e_{1}^{\text{T}}{{{\dot{e}}}_{1}}=-{{c}_{1}}e_{1}^{\text{T}}{{e}_{1}}+e_{1}^{\text{T}}{{e}_{2}}.$ | (15) |
根据式(13)并结合式(15),定义Lyapunov函数
| ${{V}_{2}}={{V}_{1}}+0.5e_{2}^{\text{T}}{{e}_{2}}=0.5e_{1}^{\text{T}}{{e}_{1}}+0.5e_{2}^{\text{T}}{{e}_{2}}.$ | (16) |
对式(16)进行求导,并对相关参数进行替代,可得
| $\begin{align} & {{{\dot{V}}}_{2}}=-{{c}_{1}}e{{_{1}^{\text{T}}}_{1}}{{e}_{1}}+e_{1}^{\text{T}}{{e}_{2}}+e_{2}^{\text{T}}{{{\dot{e}}}_{2}}= \\ & e_{2}^{\text{T}}({{\left( {{M}_{11}} \right)}^{-1}}_{0}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{0}}-{{\left( {{M}_{11}} \right)}^{-1}}_{0}{{\left( {{f}_{1}} \right)}_{0}}+ \\ & {{c}_{1}}{{{\dot{e}}}_{1}}-{{{\ddot{X}}}_{\text{d}}})-{{c}_{1}}e{{_{1}^{\text{T}}}_{1}}{{e}_{1}}+e_{1}^{\text{T}}{{e}_{2}}. \\ \end{align}$ | (17) |
根据式(17)可得
| $\begin{align} & {{\tau }_{0}}={{(J_{{{p}^{\theta }}}^{\text{T}})}^{-1}}({{({{f}_{1}})}_{0}}+{{({{M}_{11}})}_{0}}(-{{c}_{1}}{{{\dot{e}}}_{1}}+{{{\ddot{X}}}_{\text{d}}}- \\ & {{c}_{2}}{{e}_{2}}-{{e}_{1}}))={{\left( J_{{{p}^{\theta }}}^{\text{T}} \right)}^{-1}}({{\left( {{f}_{1}} \right)}_{0}}+{{\left( {{M}_{11}} \right)}_{0}}({{{\ddot{X}}}_{\text{d}}}- \\ & \left( {{c}_{1}}+{{c}_{2}} \right){{{\dot{e}}}_{1}}-\left( {{c}_{1}}{{c}_{2}}+1 \right){{e}_{1}})). \\ \end{align}$ | (18) |
其中c2为正实数,将式(18)导入方程(17),可得
| ${{{\dot{V}}}_{2}}=-{{c}_{1}}e_{1}^{\text{T}}{{e}_{1}}-{{c}_{2}}e_{2}^{\text{T}}{{e}_{2}}\le 0.$ |
因此根据Lyapunov稳定性原理,在τ0作用下,慢速子系统是稳定的. 由于弹性环节的存在,并联机器人末端位置可表示为
| $r={{X}_{1}}+{{f}_{3}}(\eta ,{{h}_{10}},{{h}_{11}},{{h}_{12}},\varepsilon ).$ | (19) |
其中f3为杆件弹性变形与振动对动平台中心G产生的弹性位移,即末端动平台的弹性位移.
根据速度映射关系,弹性运动部分产生的动平台加速度可表示为
| ${{\varepsilon }^{2}}\overset{.}{\mathop{\overline{J_{{{p}^{\theta }}}^{-1}}}}\,{{\phi }_{l}}\left( {{{\dot{h}}}_{10}}+\varepsilon {{{\dot{h}}}_{11}}+{{\varepsilon }^{2}}{{{\dot{h}}}_{12}} \right)/{{l}_{1}}.$ |
其中$\overset{.}{\mathop{\overline{J_{{{p}^{\theta }}}^{-1}}}}\,$为$J_{{{p}^{\theta }}}^{-1}$对时间的导数.
本文考察的柔性环节都在小变形范围内,因杆件弹性位移产生的动平台末端弹性位移f3可简化为
| ${{f}_{3}}={{\varepsilon }^{2}}J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}\left( {{h}_{10}}+\varepsilon {{h}_{11}}+{{\varepsilon }^{2}}{{h}_{12}} \right)/{{l}_{1}}.$ | (20) |
对方程(19)求二阶导数,考虑刚柔耦合运动时,末端动平台加速度可表示为
| $\begin{align} & \ddot{r}={{{\ddot{X}}}_{\text{d}}}+({{c}_{1}}+{{c}_{2}})({{{\dot{X}}}_{\text{d}}}-\eta \cdot )+({{c}_{1}}{{c}_{2}}+1)({{X}_{\text{d}}}-\eta )+ \\ & M_{11}^{-1}J_{{{p}^{\theta }}}^{\text{T}}\left( \varepsilon {{\tau }_{1}}+{{\varepsilon }^{2}}{{\tau }_{2}} \right)+{{\varepsilon }^{2}}\left( J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\ddot{h}}}_{10}}+\dot{\bar{J}}_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}} \right)/{{l}_{1}}- \\ & M_{11}^{-1}{{({{f}_{1}})}_{20}}{{h}_{10}}+{{({{f}_{1}})}_{21}}{{{\dot{h}}}_{10}}){{\varepsilon }^{2}}/2+ \\ & {{J}_{12}}({{J}_{22}})_{0}^{-1}{{({{J}_{22}})}_{2}}({{({{f}_{2}})}_{0}}+{{h}_{10}}){{\varepsilon }^{2}}/2+ \\ & {{J}_{12}}({{J}_{22}})_{0}^{-1}{{{\ddot{h}}}_{10}}{{\varepsilon }^{2}}+{{J}_{12}}{{({{f}_{2}})}_{21}}{{{\dot{h}}}_{10}}{{\varepsilon }^{2}}/2. \\ \end{align}$ | (21) |
定义动平台末端跟踪的位置误差${{e}_{3}}={{X}_{\text{d}}}-r$与速度误差${{e}_{4}}={{{\dot{e}}}_{3}}$,方程(21)可转化为以下状态方程形式:
| $\left\{ \begin{align} & {{{\dot{e}}}_{3}}={{e}_{4}}, \\ & {{{\dot{e}}}_{4}}=-({{c}_{1}}+{{c}_{2}}){{e}_{4}}-({{c}_{1}}{{c}_{2}}+1){{e}_{3}}- \\ & M_{11}^{-1}J_{{{p}^{\theta }}}^{\text{T}}\left( \varepsilon {{\tau }_{1}}+{{\varepsilon }^{2}}{{\tau }_{2}} \right)-{{\varepsilon }^{2}}{{J}_{12}}\left( {{J}_{22}} \right)_{0}^{-1}{{{\ddot{h}}}_{10}}- \\ & {{\varepsilon }^{2}}\left( J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\ddot{h}}}_{10}}+\overset{.}{\mathop{\overline{J_{{{p}^{\theta }}}^{-1}}}}\,{{\phi }_{l}}{{{\dot{h}}}_{10}} \right)/{{l}_{1}}+ \\ & {{\varepsilon }^{2}}M_{11}^{-1}\left( {{\left( {{f}_{1}} \right)}_{20}}{{h}_{10}}+{{\left( {{f}_{1}} \right)}_{21}}{{{\dot{h}}}_{10}} \right)/2- \\ & {{\varepsilon }^{2}}{{J}_{12}}\left( {{J}_{22}} \right)_{0}^{-1}{{\left( {{J}_{22}} \right)}_{2}}{{\left( {{f}_{2}} \right)}_{0}}+{{h}_{10}})/2- \\ & {{\varepsilon }^{2}}\left( {{c}_{1}}+{{c}_{2}} \right)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}}/{{l}_{1}}-{{\varepsilon }^{2}}{{J}_{12}}{{\left( {{f}_{2}} \right)}_{21}}{{{\dot{h}}}_{10}}/2- \\ & {{\varepsilon }^{2}}\left( {{c}_{1}}{{c}_{2}}+1 \right)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{h}_{10}}/{{l}_{1}}. \\ \end{align} \right.$ | (22) |
根据方程(22),定义Lyapunov函数
| ${{V}_{3}}=0.5e_{3}^{\text{T}}({{c}_{1}}{{c}_{2}}+1){{e}_{3}}+0.5e_{4}^{\text{T}}{{e}_{4}}.$ | (23) |
对式(23)求导可得
| $\begin{align} & {{{\dot{V}}}_{3}}=0.5e_{3}^{\text{T}}({{c}_{1}}{{c}_{2}}+1)){{{\dot{e}}}_{3}}+0.5e_{4}^{\text{T}}{{{\dot{e}}}_{4}}= \\ & -0.5e_{4}^{\text{T}}\left( {{c}_{1}}+{{c}_{2}} \right){{e}_{4}}+ \\ & 0.5e_{4}^{\text{T}}(-{{M}^{-1}}_{11}J_{{{p}^{\theta }}}^{\text{T}}\left( \varepsilon {{\tau }_{1}}+{{\varepsilon }^{2}}{{\tau }_{2}} \right)- \\ & {{\varepsilon }^{2}}\left( J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\ddot{h}}}_{10}}+\dot{\bar{J}}_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}} \right)/{{l}_{1}}+ \\ & {{\varepsilon }^{2}}M_{11}^{-1}\left( {{\left( {{f}_{1}} \right)}_{20}}{{h}_{10}}+{{\left( {{f}_{1}} \right)}_{21}}{{{\dot{h}}}_{10}} \right)/2- \\ & {{\varepsilon }^{2}}{{J}_{12}}\left( {{J}_{22}} \right)_{0}^{-1}{{\left( {{J}_{22}} \right)}_{2}}\left( {{\left( {{f}_{2}} \right)}_{0}}+{{h}_{10}} \right)/2- \\ & {{\varepsilon }^{2}}\left( {{c}_{1}}+{{c}_{2}} \right)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}}/{{l}_{1}}-{{\varepsilon }^{2}}{{J}_{12}}{{\left( {{J}_{22}} \right)}^{-1}}_{0}{{{\ddot{h}}}_{10}}- \\ & {{\varepsilon }^{2}}\left( {{c}_{1}}{{c}_{2}}+1 \right)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{h}_{10}}/{{l}_{1}}-\text{ }{{\varepsilon }^{2}}{{J}_{12}}{{\left( {{f}_{2}} \right)}_{21}}{{{\dot{h}}}_{10}}/2) \\ \end{align}$ |
令ε及ε2的系数项为零,可得校正力矩为
| $\left\{ \begin{align} & {{\tau }_{1}}=0, \\ & {{\tau }_{2}}=-{{(J_{{{p}^{\theta }}}^{\text{T}})}^{-1}}{{M}_{11}}(({{c}_{1}}+{{c}_{2}}~)(J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}})/{{l}_{1}}+ \\ & \left( {{c}_{1}}{{c}_{2}}+1 \right)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{h}_{10}}/{{l}_{1}}-M_{11}^{-1}({{\left( {{f}_{1}} \right)}_{20}}{{h}_{10}}+ \\ & {{\left( {{f}_{1}} \right)}_{21}}{{{\dot{h}}}_{10}})/2+{{J}_{12}}\left( {{J}_{22}} \right)_{0}^{-1}{{\left( {{J}_{22}} \right)}_{2}}\left( {{f}_{2}}+{{h}_{10}} \right)/2+ \\ & {{J}_{12}}\left( {{J}_{22}} \right)_{0}^{-1}{{{\ddot{h}}}_{10}}+(J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\ddot{h}}}_{10}}+ \\ & \overset{.}{\mathop{\overline{J_{{{p}^{\theta }}}^{-1}}}}\,{{\phi }_{l}}{{{\dot{h}}}_{10}})/{{l}_{1}}+{{J}_{12}}{{\left( {{f}_{2}} \right)}_{21}}{{{\dot{h}}}_{10}}/2). \\ \end{align} \right.$ | (24) |
此时,${{{\dot{V}}}_{3}}=-e_{4}^{\text{T}}\left( {{c}_{1}}+{{c}_{2}} \right){{e}_{4}}\le 0$,系统稳定,实现了对末端位姿的弹性位移补偿.
4 基于滑模变结构的快速子系统控制定义新的时间尺度tf=t/ε,快速子系统微分方程(12)可表示为
| $\begin{align} & \text{d}{{X}_{{{f}_{1}}}}/\text{d}{{t}_{f}}={{X}_{{{f}_{2}}}}, \\ & \text{d}{{X}_{{{f}_{2}}}}/\text{d}{{t}_{f}}=J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}- \\ & {{\varepsilon }^{2}}\left( {{\left( {{J}_{22}} \right)}_{2}}+J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{20}} \right){{X}_{{{f}_{1}}}}/2- \\ & \varepsilon J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{21}}{{X}_{{{f}_{2}}}}/2. \\ \end{align}$ |
第2个方程后两项含小参数ε,相对于其他项其控制量较小,可以将其视为扰动,因此扰动项可表示为
| $\begin{array}{*{35}{l}} {{\Delta }_{1}}={{\varepsilon }^{2}}\left( {{\left( {{J}_{22}} \right)}_{2}}+J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{20}} \right){{X}_{{{f}_{1}}}}/2- \\ \varepsilon \left( J_{12}^{\text{T}}{{\left( {{f}_{1}} \right)}_{21}}+{{\left( {{J}_{22}} \right)}_{0}}{{\left( {{f}_{2}} \right)}_{21}} \right){{X}_{{{f}_{2}}}}/2. \\ \end{array}$ |
由于扰动项的存在,快速子系统采用滑模变结构控制,选择滑模面为
| $St={{K}_{f}}{{X}_{{{f}_{1}}}}+{{X}_{{{f}_{2}}}}.$ |
其中K1为正数,对滑模面求导得
| $\dot{S}\left( t \right)={{K}_{f}}X+J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}.$ |
根据滑模面,定义Lyapunov函数为
| ${{V}_{4}}=0.5{{S}^{\text{T}}}S.$ |
求导可得
| ${{{\dot{V}}}_{4}}={{S}^{\text{T}}}\dot{S}={{S}^{\text{T}}}({{K}_{f}}{{X}_{{{f}_{2}}}}+J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}).$ | (25) |
根据式(25),取快速子系统控制律为
| $\begin{array}{l} {\tau _f} = {(J_{12}^{\rm{T}}J_{{p^\theta }}^{\rm{T}})^{ - 1}}( - {K_f}{X_{{f_2}}} + {({J_{22}})_0}{X_{{f_1}}} - \\ {K_f}S + {\Delta _1}{\mathop{\rm sgn}} (S)). \end{array}$ | (26) |
其中sgn(·)为符号函数,将式(26)代入式(25)得
| $\begin{align} & {{{\dot{V}}}_{4}}={{S}^{\text{T}}}({{K}_{f}}X+J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}})= \\ & -{{\Delta }_{1}}\left| S \right|-{{\Delta }_{1}}S-{{S}^{\text{T}}}{{K}_{f}}S\le -{{S}^{\text{T}}}{{K}_{f}}S\le 0. \\ \end{align}$ |
由此可知,在式(26)作用下,快速子系统是收敛的. 符号函数会对系统产生抖动,为了降低抖动的产生,将饱和函数sat(·)代替符号函数,饱和函数可定义为[20]
| $sat({{s}_{1}})=\left\{ \begin{align} & 1,{{s}_{1}}>{{\Delta }_{2}}; \\ & {{s}_{1}}/{{\Delta }_{2}},|{{s}_{1}}|\le {{\Delta }_{2}}; \\ & -1,{{s}_{1}}<-{{\Delta }_{2}}. \\ \end{align} \right.$ |
其中Δ2为缓冲层.
5 曲率变化率高增益观测器为避免对曲率变化率直接测量,本文设计高增益观测器,通过测量得到的曲率观测曲率变化率. 由方程(11)可知,快速子系统变量Xf1对应曲率值,可以通过测量应力直接换算得到,Xf2对应曲率变化率,为观测器观测值,根据文献[21]、[22]与式(4),观测器可表示为
| $\left\{ \begin{align} & \varepsilon {{{\dot{\hat{X}}}}_{f1}}={{{\hat{X}}}_{f2}}+\varepsilon _{1}^{-1}{{H}_{p}}({{X}_{f1}}-{{{\hat{X}}}_{f1}}) \\ & \varepsilon \dot{\hat{X}}f2=\varepsilon _{1}^{-2}{{H}_{v}}({{X}_{f1}}{{{\hat{X}}}_{f1}}). \\ \end{align} \right.$ | (27) |
其中${{{\hat{X}}}_{f1}}$与${{{\hat{X}}}_{f2}}$分别为Xf1与Xf2的估计值,ε1为极小的正数,Hp与Hv为常矩阵,定义观测器观测误差为
| $\left\{ \begin{align} & \tilde{X}{{~}_{f1}}={{{\hat{X}}}_{f1}}-X{{~}_{f1}}, \\ & {{{\tilde{X}}}_{~f2}}={{{\hat{X}}}_{~f2}}-{{X}_{~f2}}. \\ \end{align} \right.$ |
为证明系统稳定性,定义新的误差变量为
| $\left\{ \begin{align} & {{{\tilde{Z}}}_{{{f}_{1}}}}={{{\tilde{X}}}_{{{f}_{1}}}}, \\ & {{{\tilde{Z}}}_{{{f}_{2}}}}={{\varepsilon }_{1}}{{{\tilde{X}}}_{{{f}_{2}}}}. \\ \end{align} \right.$ | (28) |
将式(28)代入式(27),状态观测器可表示为
| $\begin{align} & \varepsilon {{\varepsilon }_{1}}{{{\dot{\tilde{Z}}}}_{{{f}_{1}}}}={{{\tilde{Z}}}_{{{f}_{2}}}}{{H}_{p}}{{{\tilde{Z}}}_{{{f}_{1}}}}, \\ & \varepsilon {{\varepsilon }_{1}}{{{\dot{\tilde{Z}}}}_{{{f}_{2}}}}=-{{H}_{v}}{{{\tilde{Z}}}_{{{f}_{1}}}}+\varepsilon {{\varepsilon }^{2}}_{1}(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}- \\ & {{\left( {{J}_{22}} \right)}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}) \\ \end{align}$ | (29) |
式(29)可改写为
| $\varepsilon {{\varepsilon }_{1}}{{{\dot{\tilde{Z}}}}_{f}}={{A}_{0}}{{{\tilde{Z}}}_{f}}+\varepsilon \varepsilon _{1}^{2}{{B}_{0}}(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}).$ |
其中: ${{A}_{0}}=\left[ \begin{matrix} -{{H}_{p}} & {{I}_{3\times 3}} \\ -{{H}_{v}} & {{0}_{3\times 3}} \\ \end{matrix} \right]\text{ }{{B}_{0}}=\left[ \begin{matrix} {{0}_{3\times 3}} \\ {{I}_{3\times 3}} \\ \end{matrix} \right]$,可以通过选择Hp与Hv来保证A0所有特征值实部均为负,即A0为Hurwitz矩阵,定义新的Lyapunov函数
| ${{V}_{5}}=\tilde{Z}_{f}^{\text{T}}{{P}_{1}}{{{\tilde{Z}}}_{f}}.$ |
其中P1为正定对称矩阵,求导可得
| $\begin{align} & {{{\dot{V}}}_{5}}={{(\varepsilon {{\varepsilon }_{1}})}^{-1}}(\tilde{Z}_{f}^{\text{T}}(A_{0}^{T}{{P}_{1}}+{{P}_{1}}{{A}_{0}}){{{\tilde{Z}}}_{f}}+2\varepsilon \varepsilon _{1}^{2}\cdot \\ & {{(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}\text{-}{{\Delta }_{1}})}^{\text{T}}}B_{0}^{T}{{P}_{1}}{{{\tilde{Z}}}_{f}}). \\ \end{align}$ |
由于A0为Hurwitz矩阵,存在正定矩阵P1,使
| $A_{0}^{T}{{P}_{1}}+{{P}_{1}}{{A}_{0}}=-{{I}_{3\times 3}}.$ |
${{{\dot{V}}}_{5}}$可改写为
| $\begin{align} & {{{\dot{V}}}_{5}}\le -{{(\varepsilon {{\varepsilon }_{1}})}^{-1}}\|{{{\tilde{Z}}}_{f}}{{\|}^{2}}+2{{\varepsilon }_{1}}\|(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}- \\ & {{\left( {{J}_{22}} \right)}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}{{)}^{\text{T}}}B_{0}^{T}{{P}_{1}}\|\|{{{\tilde{Z}}}_{f}}\|. \\ \end{align}$ | (30) |
由式(30)可知,当ε12满足
| $\varepsilon _{1}^{2}\le 2\|{{(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}})}^{\text{T}}}B_{0}^{T}{{P}_{1}}/\|\varepsilon {{{\tilde{Z}}}_{f}}\|$ | (31) |
时,${{{\dot{V}}}_{5}}$≤0成立,即高增益观测器渐进收敛. 因此,根据式(31)即可求出小参数上界,此时快速子系统力矩可表示为
| $\begin{align} & \tau f={{(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}})}^{-1}}(-{{K}_{f}}{{{\hat{X}}}_{f2}}+{{({{J}_{22}})}_{0}}{{{\hat{X}}}_{f1}}- \\ & {{K}_{f}}\hat{S}+{{\Delta }_{1}}sat(\hat{S})). \\ \end{align}$ |
其中:$\hat{S}={{K}_{f}}{{{\hat{X}}}_{{{f}_{1}}}}+{{{\hat{X}}}_{f2}}.$.根据式(12)、(29),快速子系统误差方程可表示为
| $\varepsilon \dot{\xi }={{A}_{\xi }}\xi +{{h}_{\xi }}.$ | (32) |
其中:$\xi =\left[ \begin{matrix} {{X}_{f}} & {{{\tilde{Z}}}_{f}} \\ \end{matrix} \right]{{~}^{\text{T}}}{{X}_{f}}=\left[ \begin{matrix} {{X}_{{{f}_{1}}}} & {{X}_{{{f}_{2}}}} \\ \end{matrix} \right]{{~}^{\text{T}}}$,
| $\begin{align} & {{A}_{\xi }}=\left[ \begin{matrix} {{A}_{\xi 11}} & {{A}_{\xi 12}} \\ 0 & {{A}_{0}}/{{\varepsilon }_{1}} \\ \end{matrix} \right]{{A}_{\xi 11}}=\left[ \begin{matrix} {{0}_{3\times 3}} & {{I}_{3\times 3}} \\ -K_{f}^{2} & -2{{K}_{f}} \\ \end{matrix} \right], \\ & {{A}_{\xi 12}}=\left[ \begin{matrix} {{0}_{3\times 3}} & {{I}_{3\times 3}} \\ {{({{J}_{22}})}_{0}}-K_{f}^{2} & -2{{K}_{f}} \\ \end{matrix} \right], \\ & {{h}_{\xi }}=\left[ \begin{matrix} {{\Delta }_{1}}sat(\hat{S})-{{\Delta }_{1}} \\ \varepsilon {{\varepsilon }_{1}}{{B}_{0}}(J_{12}^{\text{T}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{({{J}_{22}})}_{0}}{{X}_{{{f}_{1}}}}-{{\Delta }_{1}}) \\ \end{matrix} \right]. \\ \end{align}$ |
根据误差方程(32),可定义Lyapunov函数
| ${{V}_{6}}=\varepsilon {{\xi }^{\text{T}}}{{P}_{\xi }}\xi .$ | (33) |
其中Pξ为对称正定矩阵,式(33)求导可得
| $\begin{align} & {{{\dot{V}}}_{6}}=\varepsilon {{\xi }^{\text{T}}}\left( A_{\xi }^{\text{T}}{{P}_{\xi }}+P_{\xi }^{\text{T}}{{A}_{\xi }} \right)\xi +2h_{\xi }^{\text{T}}{{P}_{\xi }}\xi + \\ & \varepsilon {{\xi }^{\text{T}}}{{{\dot{P}}}_{\xi }}\xi . \\ \end{align}$ | (34) |
由于Aξ11与A0均为Hurwitz矩阵,对于给定的对称正定阵Sξ,存在对称正定矩阵Pξ满足
| $A_{\xi }^{\text{T}}{{P}_{\xi }}+P_{\xi }^{\text{T}}{{A}_{\xi }}=-{{S}_{\xi }}.$ | (35) |
根据Rayleigh-Ritz不等式可知:
| $-{{\xi }^{\text{T}}}{{S}_{\xi }}\xi \le -{{\lambda }_{\min }}{{S}_{\xi }}\|\xi {{\|}^{2}},$ | (36) |
| $\|h_{\xi }^{\text{T}}{{P}_{\xi }}\xi \|\le \left( {{\chi }_{0}}+{{\chi }_{1}}{{\varepsilon }_{1}} \right)\|\xi \|,\|{{{\dot{P}}}_{\xi }}\|\le {{\chi }_{2}}.$ | (37) |
其中λmin(·)分别表示对应矩阵的最小特征值,χ0、 χ1、χ2为正实数. 根据方程(35)~(37),方程(34)可表示为
| ${{{\dot{V}}}_{6}}\le -{{\lambda }_{\min }}({{S}_{\xi }})\|\xi {{\|}^{2}}+\varepsilon {{\chi }_{2}}\|\xi {{\|}^{2}}+2({{\chi }_{0}}+{{\chi }_{1}}{{\varepsilon }_{1}})\|\xi \|.$ | (38) |
根据式(38),当${{{\dot{V}}}_{6}}$≤0时,高增益观测器中小参数满足0≤ε1≤ε1max, 此时基于高增益观测器的快速子系统稳定,其中小参数上界满足以下要求:
| ${{\varepsilon }_{1\max }}\le {{\lambda }_{\min }}{{S}_{\xi }}\|\xi \|-\varepsilon {{\chi }_{2}}\|\xi \|-2{{\chi }_{0}}/{{\chi }_{1}}.$ | (39) |
各子系统稳定性并不能保证系统整体稳定性,因此需要综合各子系统对系统整体稳定性进行证明. 将式(9)、(18)、(24)分别代入动力学式(3)可以得系统误差方程为
| $\begin{align} & {{{\dot{e}}}_{s}}={{A}_{s}}{{e}_{s}}+{{h}_{s}}, \\ & \varepsilon \dot{\xi }={{A}_{\xi }}\xi +{{h}_{\xi }}. \\ \end{align}$ |
式中:
| $\begin{align} & {{e}_{s}}={{\left[ \begin{matrix} {{X}_{1}}-{{X}_{\text{d}}} & {{{\dot{X}}}_{1}}-{{{\dot{X}}}_{\text{d}}} \\ \end{matrix} \right]}^{\text{T}}},{{h}_{s}}={{\left[ \begin{matrix} 0 & {{h}_{s1}} \\ \end{matrix} \right]}^{\text{T}}}, \\ & {{A}_{s}}=\left[ \begin{matrix} {{0}_{3\times 3}} & {{I}_{3\times 3}} \\ -\left( {{c}_{1}}{{c}_{2}}+1 \right){{I}_{3\times 3}} & -\left( {{c}_{1}}+{{c}_{2}} \right){{I}_{3\times 3}} \\ \end{matrix} \right], \\ & {{h}_{s1}}={{J}_{11}}J_{{{p}^{\theta }}}^{\text{T}}{{\tau }_{f}}-{{J}_{12}}{{X}_{{{f}_{1}}}}-{{\varepsilon }^{2}}{{J}_{11}}{{M}_{11}}(({{c}_{1}}+ \\ & {{c}_{2}})J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}}/{{l}_{1}}+({{c}_{1}}{{c}_{2}}+1)J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{h}_{10}}/{{l}_{1}}+ \\ & \left( J_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\ddot{h}}}_{10}}+\dot{\bar{J}}_{{{p}^{\theta }}}^{-1}{{\phi }_{l}}{{{\dot{h}}}_{10}} \right)/{{l}_{1}}). \\ \end{align}$ |
根据误差方程,定义整体系统的Lyapunov函数为
| ${{V}_{7}}=e_{s}^{\text{T}}{{P}_{s}}{{e}_{s}}+\varepsilon {{\xi }^{\text{T}}}{{P}_{\xi }}\xi .$ | (40) |
其中Ps与Pξ为对称正定矩阵,对式(40)求导得
| $\begin{align} & {{{\dot{V}}}_{7}}=e_{s}^{\text{T}}\left( A_{s}^{\text{T}}{{P}_{s}}+P_{s}^{\text{T}}{{A}_{s}} \right){{e}_{s}}+{{\xi }^{\text{T}}}\left( A_{\xi }^{\text{T}}{{P}_{\xi }}+P_{\xi }^{\text{T}}{{A}_{\xi }} \right)\xi + \\ & 2h{{_{s}^{\text{T}}}_{s}}{{P}_{s}}{{e}_{s}}+2h_{\xi }^{\text{T}}{{P}_{\xi }}\xi +\varepsilon {{\xi }^{\text{T}}}{{{\dot{P}}}_{\xi }}\xi . \\ \end{align}$ | (41) |
由于As为Hurwitz矩阵,对于给定的对称正定阵Ss,存在对称正定矩阵Ps满足以下条件:
| $A_{s}^{\text{T}}{{P}_{s}}+P_{s}^{\text{T}}{{A}_{s}}=-{{S}_{s}}.$ | (42) |
根据方程(35)与(41)、(42),${{{\dot{V}}}_{7}}$可改写为
| $\begin{align} & {{{\dot{V}}}_{7}}=-e_{s}^{\text{T}}{{S}_{s}}{{e}_{s}}-{{\xi }^{\text{T}}}{{S}_{\xi }}\xi +2h{{_{s}^{\text{T}}}_{s}}{{P}_{s}}{{e}_{s}}+ \\ & 2h_{\xi }^{\text{T}}{{P}_{\xi }}\xi +\varepsilon {{\xi }^{\text{T}}}{{{\dot{P}}}_{\xi }}\xi . \\ \end{align}$ |
根据Rayleigh-Ritz不等式可知
| $-e_{s}^{\text{T}}{{S}_{s}}{{e}_{s}}\le -{{\lambda }_{\min }}({{S}_{s}})\|{{e}_{s}}{{\|}^{2}}$ | (43) |
| $-{{\xi }^{\text{T}}}{{S}_{\xi }}\xi \le -{{\lambda }_{\min }}{{S}_{\xi }}\|\xi {{\|}^{2}},$ | (44) |
| $\|h_{s}^{\text{T}}{{P}_{s}}{{e}_{s}}\|\le ({{\chi }_{3}}+{{\chi }_{4}}\varepsilon +{{\chi }_{5}}{{\varepsilon }^{2}})\|{{e}_{s}}\|\|\xi \|,$ | (45) |
| $\|h_{\xi }^{\text{T}}{{P}_{\xi }}\xi \|\le ({{\chi }_{6}}+{{\chi }_{7}}\varepsilon +{{\chi }_{8}}{{\varepsilon }^{2}})\|\xi {{\|}^{2}}.$ | (46) |
式中,χi(i=0,1,…,6)为正数,由方程(43)~(46)可知,${{{\dot{V}}}_{7}}$满足以下关系:
| $\begin{align} & {{{\dot{V}}}_{7}}\le -[\|{{e}_{s}}\|\|\xi \|]\cdot \\ & \left[ \begin{matrix} {{\lambda }_{\min }}\left( {{S}_{s}} \right) & -({{\chi }_{3}}+{{\chi }_{4}}\varepsilon +{{\chi }_{5}}{{\varepsilon }^{2}}) \\ -\left( {{\chi }_{3}}+{{\chi }_{4}}\varepsilon +{{\chi }_{5}}{{\varepsilon }^{2}} \right) & {{\lambda }_{\min }}({{S}_{\xi }})-2({{\chi }_{6}}+{{\chi }_{7}}\varepsilon +{{\chi }_{8}}{{\varepsilon }^{2}})-{{\chi }_{2}}\varepsilon \\ \end{matrix} \right]. \\ & \left[ \begin{matrix} \|{{e}_{s}}\| \\ \|\xi \| \\ \end{matrix} \right]. \\ \end{align}$ | (47) |
闭环系统渐进稳定的条件是${{{\dot{V}}}_{7}}$≤0,从式(47)可知,${{{\dot{V}}}_{7}}$≤0的条件为系数矩阵正定,即
| $\begin{align} & {{\lambda }_{\min }}({{S}_{s}})({{\lambda }_{\min }}({{S}_{\xi }})-2({{\chi }_{6}}+{{\chi }_{7}}\varepsilon +{{\chi }_{8}}{{\varepsilon }^{2}})- \\ & {{\chi }_{2}}\varepsilon )-{{({{\chi }_{3}}+{{\chi }_{4}}\varepsilon +{{\chi }_{5}}{{\varepsilon }^{2}})}^{2}}\ge 0. \\ \end{align}$ |
忽略O(ε2)高次项的影响,小参数ε的最大值满足
| ${{\varepsilon }_{\max }}=(-{{\lambda }_{b}}+\sqrt{\lambda _{b}^{2}+4{{\lambda }_{a}}{{\lambda }_{c}}})/(2{{\lambda }_{a}})$ |
条件时,${{{\dot{V}}}_{7}}$≤0成立. 其中,
| $\begin{align} & {{\lambda }_{a}}={{\lambda }_{min}}({{S}_{s}}){{\chi }_{8}}+{{\chi }^{2}}_{4}+2{{\chi }_{3}}{{\chi }_{5}}, \\ & {{\lambda }_{b}}=-2{{\lambda }_{\min }}({{S}_{s}}){{\chi }_{7}}-{{\lambda }_{\min }}({{S}_{s}}){{\chi }_{2}}-2{{\chi }_{3}}{{\chi }_{4}}, \\ & {{\lambda }_{c}}={{\lambda }_{\min }}({{S}_{s}}){{\lambda }_{\min }}({{S}_{\xi }})-2{{\lambda }_{\min }}({{S}_{s}}){{\chi }_{6}}-\chi _{3}^{2}. \\ \end{align}$ |
由式(47)可知,当ε的取值满足0<ε≤εmax时,整体系统是稳定的.
7 算法仿真为对本文提出的复合控制进行验证,将其与奇异摄动控制及仅考虑刚体动力学模型的反演控制进行对比,上述算法仿真在MATLAB软件的SIMULINK模块下开展,并选用ode15s积分器. 由式(24)可知,在基于积分流形与观测器的复合控制算法中,动平台末端位姿的期望轨迹需满足四阶导数连续,为减小期望轨迹在起始与末端点对系统的冲击,期望轨迹采用式(48)所示的九次多项式规划,保证起始与末端点处的速度、加速度、三阶与四阶导数为零.
| $\left\{ \begin{align} & {{p}_{x}}={{A}_{0}}(125{{t}^{5}}/t_{\text{d}}^{5}-420{{t}^{6}}/t_{\text{d}}^{6}+540{{t}^{7}}/t_{\text{d}}^{7}- \\ & 315{{t}^{8}}/t_{\text{d}}^{8}+70{{t}^{9}}/t_{\text{d}}^{9})+{{p}_{{{x}_{0}}}}, \\ & {{p}_{y}}={{p}_{{{y}_{0}}}}, \\ & \phi =0. \\ \end{align} \right.$ | (48) |
式中: 运行时间td=0.06s,期望轨迹的起始位置px0=187.5,py0=187.5/3,幅度A0=30. 取${{\varepsilon }^{2}}=1/{{k}_{s}}{{H}_{p}}=\text{diag}([40,~40,~40])$,${{\Delta }_{1}}={{[\begin{matrix} 1\times {{10}^{-3}} & 1\times {{10}^{-3}} & 1\times {{10}^{-3}} \\ \end{matrix}~~]}^{\text{T}}}$,${{c}_{1}}={{c}_{2}}=50,{{H}_{v}}=\text{diag}([400,~400,~400])$,${{\Delta }_{2}}=0.05{{K}_{f}}=\text{diag}([60,~60,~60])$.根据方程(39),取ε1=0.001. 对文献[17]增加与修改的参数如下:杆件高度与厚度分别为30 mm与5 mm,减速比为20,电机与减速机转动惯量和为284.1 kg·mm2.
为描述末端性能,引入平均误差,定义为
| $\begin{align} & {{t}_{\text{M}}}=(t_{\text{d}}^{-1}\int\limits_{0}^{{{t}_{\text{d}}}}{({{C}_{R}}{{\left( 1 \right)}^{2}}+{{C}_{R}}{{\left( 2 \right)}^{2}})\text{d}t{{)}^{\frac{1}{2}}}} \\ & {{r}_{M}}=(t_{\text{d}}^{-1}\int\limits_{0}^{{{t}_{\text{d}}}}{{{C}_{R}}{{\left( 3 \right)}^{2}}\text{d}t{{)}^{\frac{1}{2}}}}. \\ \end{align}$ |
其中CR为末端动平台3个方向的性能指标,tM与rM分别为平动方向平均误差与转动方向平均误差.
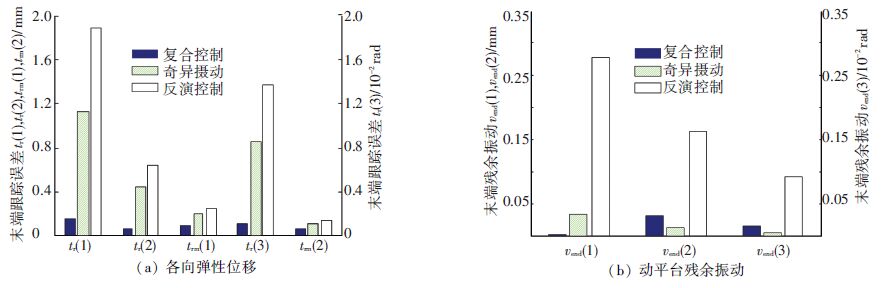
根据式(20)可计算动平台弹性位移f3. vi与vm分别表示运行过程中动平台各方向的最大弹性位移及平动与转动方向的平均弹性位移,vend表示终点时刻弹性位移即残余振动. 对于相同的期望输入,动平台弹性位移的大小可反映复合、奇异、反演3种控制算法的振动抑制效果. 各方向的弹性位移见图 4与5.

|
图 4 动平台瞬时弹性位移 Figure 4 Instantaneous flexible displacement of the moving platform |
|
图 5 动平台弹性位移与残余振动性能 Figure 5 Flexible displacement and residue vibration performance of the moving platform |
可以看出,奇异摄动与反演控制相比,各方向的最大弹性位移幅值都下降了28%以上,复合控制与奇异摄动相比下降了4.75%、33.42%与33.52%. 反演控制及奇异摄动平动方向的平均弹性位移,分别为1.579、1.112 mm,复合控制则下降到0.970 mm;对于转动方向,从反演控制及奇异摄动的0.001 4 rad及9.863×10-4 rad下降到复合控制的6.872×10-4 rad,复合控制在两个方向上弹性位移都下降了14%以上. 与反演控制相比,复合控制与奇异摄动的残余振动都有较大幅度降低,且两种算法都接近于0.
跟踪误差为末端的实际输出与期望输出的差值. tr表示动平台各方向的最大跟踪误差,trm表示平动与转动方向的平均跟踪误差,tend表示终点时刻的跟踪误差.
由图 6、7可知,与奇异摄动及反演控制器相比,基于积分流形与观测器的复合控制在轨迹跟踪方面具有明显的优势. 对于最大跟踪误差,X方向分别下降了85.56%与91.41%,Y方向分别下降了57.55%与90.57%,转动方向分别下降了53.34%与61.5%;对于平均跟踪误差,平动方向分别下降了88.2%与92.62%,转动方向分别下降了37.26%与49.57%;在终点时刻跟踪误差方面,X方向分别下降了92.8%与72.34%,Y方向分别下降了89.73%与83.62%,转动方向分别下降了85.96%与70.85%. 对于终点时刻跟踪误差,奇异摄动方法与反演控制器相比在各方向都明显变差,主要是因为奇异摄动算法只考虑了振动抑制,由于调节的延迟,在实现振动抑制时末端点轨迹跟踪性能变差.

|
图 6 动平台末端瞬时跟踪误差 Figure 6 Instantaneous tracking error of the moving platform |
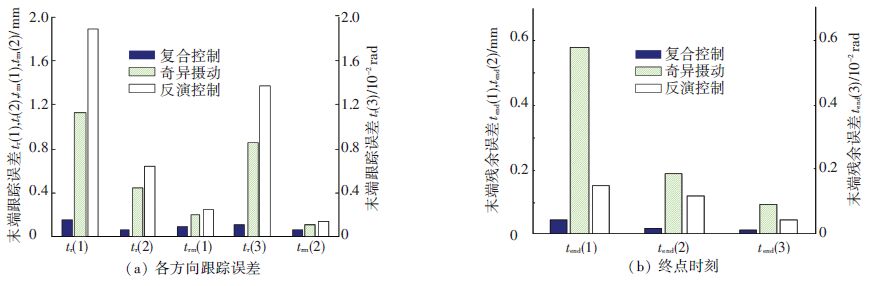
|
图 7 动平台末端跟踪误差性能 Figure 7 Tracking error performance of the moving platform |
1) 基于积分流形将刚柔耦合动力学模型降解为快速与慢速子系统,采用滑模控制与反演控制分别设计快、慢子系统控制器,并对机器人末端的弹性位移进行补偿,同时采用高增益观测器对曲率变化率进行估计,进而实现高速并联机器人的轨迹跟踪控制.
2) 选取Lyapunov函数,证明了慢速子系统、快速子系统、高增益观测器及整体系统的渐进稳定性,给出了积分流形与观测器中小参数选取条件.
3) Matlab-Simulink仿真结果表明,复合控制算法在振动抑制与轨迹跟踪方面均具有明显优势.
| [1] | PIETSCH I, KREFFT M, BECKER O, et al. How to reach the dynamic limits of parallel robots? An autonomous control approach[J]. IEEE Transactions on Automation Science and Engineering, 2005, 2 (4) : 369-380. DOI: 10.1109/TASE.2005.851600 |
| [2] | DWIVEDY S, EBERHARD P. Dynamic analysis of flexible manipulators, a literature review[J]. Mechanism and Machine Theory, 2006, 41 (7) : 749-777. DOI: 10.1016/j.mechmachtheory.2006.01.014 |
| [3] | LI Yongming, TONG Shaocheng, LI Tieshan. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping[J]. Nonlinear Analysis: Real World Applications, 2013, 14 (1) : 483-494. DOI: 10.1016/j.nonrwa.2012.07.010 |
| [4] | VAKIL M, FOTOUHI R, NIKIFORUK P. Causal end-effector inversion of a flexible link manipulator[J]. Mechatronics, 2009, 19 (7) : 1197-1210. DOI: 10.1016/j.mechatronics.2009.03.010 |
| [5] | MOALLEM M, PATEL R, KHORASANI K. Nonlinear tip-position tracking control of a flexible-link manipulator: theory and experiments[J]. Automatica, 2001, 37 (11) : 1825-1834. DOI: 10.1016/S0005-1098(01)00130-3 |
| [6] | LIZARRAGA I, ETXEBARRIA V. Combined PD-H∞ approach to control of flexible link manipulators using only directly measurable variables[J]. Cybernetics & Systems, 2003, 34 (1) : 19-31. |
| [7] | ZHANG Q, MILLS J, CLEGHORN W, et al. Trajectory tracking and vibration suppression of a 3-PRR parallel manipulator with flexible links[J]. Multibody System Dynamics, 2015, 33 (1) : 27-60. DOI: 10.1007/s11044-013-9407-2 |
| [8] | EL-BADAWY A, MEHREZ M W, ALI A R. Nonlinear modeling and control of flexible-link manipulators subjected to parametric excitation[J]. Nonlinear Dynamics, 2010, 62 (4) : 769-779. DOI: 10.1007/s11071-010-9761-z |
| [9] | SUBUDHI B, MORRIS A. Soft computing methods applied to the control of a flexible robot manipulator[J]. Applied Soft Computing, 2009, 9 (1) : 149-158. DOI: 10.1016/j.asoc.2008.02.004 |
| [10] | KHORASANI K. Adaptive control of flexible-joint robots[J]. IEEE Transactions on Robotics and Automation, 1992, 8 (2) : 250-267. DOI: 10.1109/70.134278 |
| [11] | MOALLEM M, KHORASANI K, PATEL R. An integral manifold approach for tip-position tracking of flexible multi-link manipulators[J]. IEEE Transactions on Robotics and Automation, 1997, 13 (6) : 823-837. DOI: 10.1109/70.650161 |
| [12] | SALMASI H, FOTOUHI R, NIKIFORUK P. A manoeuvre control strategy for flexible-joint manipulators with joint dry friction[J]. Robotica, 2010, 28 (4) : 621-635. DOI: 10.1017/S0263574709990373 |
| [13] | VAKIL M, FOTOUHI R, NIKIFORUK P. Application of the integral manifold concept for the end-effector trajectory tracking of a flexible link manipulator [C]//Proceedings of the 26th American Control Conference. New York: IEEE, 2007: 741-747. |
| [14] | VAKIL M, FOTOUHI R, NIKIFORUK P. End-Effector Trajectory Tracking of a Class of Flexible Link Manipulators [C]// Proceedings of 32nd Annual Mechanisms and Robotics Conference. New York: ASME, 2008: 1085-1094. |
| [15] | VAKIL M, FOTOUHI R, NIKIFORUK P. End-effector trajectory tracking of a flexible link manipulator using integral manifold concept[J]. International Journal of Systems Science, 2011, 42 (12) : 2057-2069. DOI: 10.1080/00207721003710631 |
| [16] | VAKIL M, FOTOUHI R, NIKIFORUK P. Maneuver control of the multilink flexible manipulators[J]. International Journal of Non-Linear Mechanics, 2009, 44 (8) : 831-844. DOI: 10.1016/j.ijnonlinmec.2009.05.008 |
| [17] | CHEN Z, KONG M, JI C, et al. An efficient dynamic modelling approach for high-speed planar parallel manipulator with flexible links[J]. Journal of Mechanical Engineering Science, 2015, 229 (4) : 663-678. DOI: 10.1177/0954406214538946 |
| [18] | GORIUS T, SEIFRIED R, EBERHARD P. Approximate end-effector tracking control of flexible multibody systems using singular perturbations[J]. Journal of Computational and Nonlinear Dynamics, 2013, 9 (1) : 011017. DOI: 10.1115/1.4025635 |
| [19] | ZHU Ge, LEE T, GE S. Tip tracking control of a single-link flexible robot: A backstepping approach[J]. Dynamics and Control, 1997, 7 (4) : 341-360. DOI: 10.1023/A:1008220427072 |
| [20] | LEE S, LEE C. Hybrid control scheme for robust tracking of two-link flexible manipulator[J]. Journal of Intelligent & Robotic Systems, 2001, 32 (4) : 389-410. |
| [21] | HEREDIA J, YU Wen. A high-gain observer-based PD control for robot manipulator [C] //Proceedings of the 2000 American Control Conference. Chicago: IEEE,2000: 2518-2522. |
| [22] | MOSAYEBI M, GHAYOUR M, SADIGH M. A nonlinear high gain observer based input-output control of flexible link manipulator[J]. Mechanics Research Communications, 2012, 45 : 34-41. DOI: 10.1016/j.mechrescom.2012.06.004 |
 2017, Vol. 49
2017, Vol. 49


