波箔气体动压轴承最早出现在上个世纪60年代,在之后的几十年间,理论与实验研究都获得了较快的发展[1-2],轴承的承载能力与稳定性都随着箔片结构的改进与涂层技术的发展获得了较大的提高[3]. 近十几年来,波箔轴承开始逐渐被应用在一些极限环境中,例如,微型燃气轮机、汽车涡轮增压器、透平膨胀机、空气压缩机、鼓风机等[4-6]. 即使波箔气体轴承比传统的液体轴承与滚珠轴承对高温环境有更好的适应性,但是在高转速与高温环境中,如果缺乏充分的温度控制,轴承性能会受到较大影响[7-8].
波箔气体轴承热特性的理论与实验研究一直比较匮乏,Salehi等[9]通过Couette近似,忽略了气膜压力梯度对于能量方程的影响,而将能量方程与雷诺方程解耦,单独求解了波箔轴承一维温度分布,但其建立的模型比较简单,并没有建立箔片结构与转子的热模型. Peng等[10]采用有限差分法对能量方程离散处理,在平箔片外表面采用等效对流换热系数模拟了箔片一侧的边界条件,求得了气膜三维温度分布,但是作者忽略了箔片结构的导热与换热,也没有给出明确的转子温度边界条件. Lee等[11]建立了更加完整与复杂的轴承热传递模型,考虑了波箔冷却通道的对流换热以及转子的轴向导热,给出了相对充分的热边界条件. Feng等[12]推导了箔片一侧的等效对流换热系数,同时转子内通冷却气进行冷却. 气膜径向方向采用稀疏网格建模,用Lobatto点积分来表示稀疏网格上的值,缩小了计算量,理论计算结果与之前的实验结果比较接近,但是作者简化了箔片结构来建立热模型,与实际情况有所出入. Andrés 等[13]介绍了用二维 THD 模型来研究波箔轴承的热特性. 该模型研究了轴承内热量的产生于向周围环境的传递过程,推导出了可以简化计算的等效对流换热系数,但文中作者通过对三维能量方程沿着气膜厚度对温度积分的方法的准确性没有得到验证. Salehi等[9]也进行了实验研究,在波箔通道中通入冷却气体,表明有80%热量流入外冷却通道中. Dellacorte[14]搭建了一个波箔轴承在高温环境下运行的实验台,试验台能够提供最高7×104 r/min的轴承转速与700 ℃的轴承工作环境. Radil等[15]针对第三代波箔轴承热特性进行了实验研究,在不同载荷分布(9~222 N),不同转速条件(2.0×104 ~5.0×104 r/min)下,测量了气膜温度沿圆周方向与轴向方向的分布情况.
本文考虑实际的箔片结构与冷却条件,建立了较复杂的波箔轴承能量传递模型,设立了完整的热边界条件,与实际热流状态非常接近. 数值耦合求解了气膜三维能量传递方程、能量方程与气膜厚度方程,有效地避免了之前理论研究模型的不足之处.
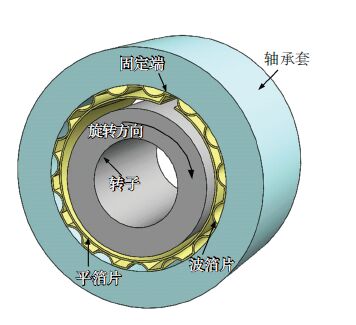
1 理论模型波箔气体动压轴承主要包括:用于形成润滑表面的平箔片,起弹性支撑作用的波形箔片,轴承套与转子. 轴承主要结构如图 1所示.
|
图 1 波箔轴承结构示意 Figure 1 Schematic of the structure of bump foil bearing |
轴承高速运行时,微米级的气膜厚度使气体分子间摩擦生热严重,较小的空气比热容使热量很难传递出去,因此会导致较大温升. 轴承内部热量传递方式与传递通道如图 2所示. 热量在气膜内部产生,一部分流向箔片结构,一部分通过轴承端部排出的气体传出,另一部分通过转子流到周围环境中.

|
图 2 轴承系统能量传递模型 Figure 2 Energy transfer model of the bearing system |
气膜内部的气体流动状态可以用Reynolds控制方程表征. 非等温条件下,稳态Reynolds方程为
| $\frac{1}{{{R^2}}}\frac{\partial }{{\partial \theta }}\left( {\frac{{p{h^3}}}{{12\mu T}}\frac{\partial }{{\partial \theta }}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{p{h^3}}}{{12\mu T}}\frac{\partial }{{\partial y}}} \right) = \frac{\omega }{2}\frac{\partial }{{\partial \theta }}\left( {\frac{{ph}}{T}} \right).$ | (1) |
式中:μ为气体黏度(Pa·s);T为气膜温度(K); x为圆周方向,x=R·θ;y为轴承宽度方向;z为气膜厚度方向;ω为转子角速度(rad/s). 气体的黏度与温度存在一定关系:
| $\mu = a(T - {T_{{\rm{ref}}}}).$ |
式中: a=4×10-8 ,Tref=-185.59K.
气膜的能量传递是由三维能量传递控制方程描述的,由于圆周方向气体流速很大,因此沿圆周方向的导热量与对流换热量相比非常小,可以忽略. 同时由于气膜很薄,气膜厚度方向的气体流速较小,则气膜厚度方向的热传导是主要的热传递形式,因此z方向的对流换热可以忽略. 简化后的能量方程为
| $\begin{align} & \rho {{c}_{p}}\left( u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y} \right)=k\left( \frac{{{\partial }^{2}}T}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{z}^{2}}} \right)+u\frac{\partial p}{\partial x}+v\frac{\partial p}{\partial y}+ \\ & \mu \left( {{\left( \frac{\partial u}{\partial z} \right)}^{2}}+{{\left( \frac{\partial v}{\partial z} \right)}^{2}} \right). \\ \end{align}$ | (2) |
式中:cp为气体定压比热容(J/(kg·K)),k为气体导热系数(W/(m·K)),u为气膜圆周方向速度(m/s),v为气膜轴向方向速度(m/s).
箔片结构的变形,高转速条件下转子的热膨胀与离心膨胀,箔片结构热膨胀都会相应地改变气膜厚度分布. 因此,非等温条件下,波箔轴承的气膜厚度可以表示为
| $h=c(1+\varepsilon \cos ~\varphi )+(p-{{p}_{\text{a}}})\cdot s/{{k}_{\text{b}}}-{{\delta }_{gc}}-\Delta {{C}_{\text{t}}}.$ | (3) |
式中:c为初始气膜间隙(m);s为波箔节距(m);kb为单位轴向波箔长度刚度(N/m2);δgc为转子离心膨胀(m);ΔCt为轴承系统热膨胀(m),ΔCt=δs+δf-δh;δs为转子外表面的热膨胀;δf为箔片结构的热膨胀;δh为轴承套内表面的热膨胀.
δgc为转子的离心膨胀,且
| ${{\delta }_{\text{gc}}}={{\rho }_{\text{s}}}R{{\omega }^{2}}/(4{{E}_{\text{s}}})[{{R}^{2}}\left( 1-\nu \right)+{{R}_{\text{in}}}^{2}\left( 3+\nu \right)].$ |
式中:ρs为转子密度,R为转子外表面半径,ω为轴承转速(rad/s),v为转子材料泊松比,Rin为空心转子内表面半径,Es为转子的弹性模量.
气膜能量方程的边界条件为
| $\begin{align} & T{{|}_{z=0}}={{T}_{\text{R}}}, \\ & T{{|}_{\theta =0}}={{T}_{\text{inlet}}}, \\ & T{{|}_{z=1}}={{T}_{\text{top}}}. \\ \end{align}$ |
式中:TR为转子表面温度(K),Tinlet为平箔片前端入口气膜温度(K),Ttop为平箔片表面温度(K).
因此气膜能量传递模型与转子热传递模型、箔片一侧导热换热模型、平箔片前端气体混合模型之间有紧密的联系. 转子外表面与平箔片内表面都和润滑气膜接触,因此接触表面上两个模型的对应点具有相同的温度,在整个接触面满足热流平衡条件. 同时,平箔片前端混合模型的输出值是气膜能量传递模型的输入值.
能量方程与Reynolds方程都是非线性二阶偏微分方程,不能够直接求解,采用有限差分法进行离散求解能够获得较高精度解. 从式(1)~(3)中可以看出,气膜能量方程、非等温Reynolds方程、气膜厚度方程之间是相互耦合的,需要通过迭代的方式得到3个方程的收敛解.
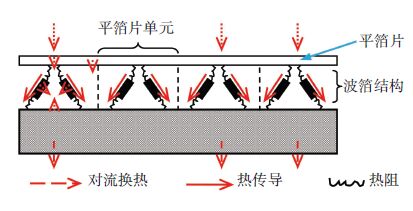
1.2 箔片结构一侧的导热换热模型气膜内部产生的热量一部分向箔片结构传递,如果波箔通道中通入冷却气,那么热流流经平箔片后,大部分通过对流换热的方式由平箔片传到冷却气流中,一部分通过热传导流经波箔片与轴承套,经自然对流换热传到环境空气中. 同时,热流也会由波箔表面与轴承套内表面传到冷却空气中,具体能量传递示意图如图 3所示.
|
图 3 箔片结构热流传递示意图 Figure 3 Schematic of heat flow transfer in the foil structure |
由气膜内部热量向平箔片传递的总热量可以分为3个部分,参照图 2,通过能量守恒可得
| ${{Q}_{\text{film}\to \text{foil}}}={{Q}_{C\to \text{coo}\lim \text{g}}}+{{Q}_{D\to \text{coo}\lim \text{g}}}+{{Q}_{E\to F}}.$ |
式中:C为平箔外表面(远离转子一侧),D
由热流传递的连续性与能量守恒条件,可以推导出平箔片内表面(靠近转子一侧)的等效对流换热系数. 气膜与平箔片内表面相接触,边界温度条件就可以表示为
| $-\gamma {{\left. \frac{\partial \bar{T}}{\partial \bar{z}} \right|}_{\bar{z}=1}}={{\left. N\bar{T} \right|}_{\bar{z}=1}}+\frac{N-{{N}_{0}}}{{{T}_{0}}-{{T}_{\text{ref}}}}{{T}_{0}}.$ | (4) |
式中:
| $\begin{align} & \gamma =\frac{{{k}_{\text{a}}}{{A}_{\text{top}}}}{h}\frac{R+h}{R+h+{{t}_{\text{f}}}}\left( 1+\frac{M{{R}_{\text{top}\_\text{bump}}}}{2} \right)+ \\ & \frac{{{k}_{\text{a}}}N\left( R+h \right)}{h\times {{k}_{\text{cond }\!\!\_\!\!\text{ t}}}}\ln \left( \frac{R+h+{{t}_{\text{f}}}}{R+h} \right), \\ & N={{h}_{\text{conv}\_\text{t}}}{{A}_{\text{top}}}+0.5M\times {{h}_{\text{conv}\_\text{t}}}{{A}_{\text{top}}}{{R}_{\text{top}\_\text{bump}}}+M- \\ & {{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A\times {{R}_{\text{bump}\_\text{h}}}/{{R}_{\text{top}\_\text{bump}}} \\ & M={{h}_{\text{conv}\_\text{b}}}{{A}_{\text{bump}}}+0.5{{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A{{h}_{\text{conv}\_\text{b}}}{{A}_{\text{bump}}}{{R}_{\text{bump}\_\text{h}}}+ \\ & {{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A+{{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A\times {{R}_{\text{bump}\_\text{h}}}/{{R}_{\text{top}\_\text{bump}}} \\ & {{M}_{0}}={{h}_{\text{conv}\_b}}{{A}_{\text{bump}}}+0.5{{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A{{h}_{\text{conv}\_\text{b}}}{{A}_{\text{bump}}}{{R}_{\text{bump}\_\text{h}}}+ \\ & {{h}_{\text{conv}\_\text{h}}}{{A}_{\text{bh}}}A \\ & {{N}_{0}}={{M}_{0}}+{{h}_{\text{conv}\_\text{t}}}{{A}_{\text{top}}}+0.5M\times {{h}_{\text{conv}\_\text{t}}}{{A}_{\text{top}}}{{R}_{\text{top}\_\text{bump}}}. \\ \end{align}$ |
式中:ka为气膜导热系数,Atop为平箔片单元面积,tf为平箔片厚度,Rtop_bump为平箔片与波箔片的接触热阻[11],hconv_t为平箔片外表面的对流换热系数,hconv_b为波箔表面的强迫对流换热系数,hconv_h为轴承套外表面的自然对流换热系数[16],Rbump_h为波箔片与轴承套之间的接触热阻[11].
推导得到的等效对流换热系数γ包括了与外部冷却条件与箔片结构特征有关的参数,并通过式(4)将复杂的箔片结构热模型归并到能量方程的一个边界条件上.
1.3 平箔片前端气体混合模型由于轴承结构的特殊性,气膜内部不会有低于大气压的情况,轴承端部排出的气体从平箔片前端补充,保证气膜间隙的气体质量守恒. 补充进来的常温气体与循环高温气体混合达到一定冷却效果. 基于热循环气流与进气冷却气流与混合气流的能量守恒条件,因此在平箔片前端的温度边界条件为
| ${{T}_{\text{in}}}=({{T}_{\text{rec}}}{{q}_{\text{rec}}}+{{T}_{\text{suc}}}{{q}_{\text{suc}}})/({{q}_{\text{rec}}}+{{q}_{\text{suc}}}).$ |
式中:Tin为平箔片前端的混合入口温度,Trec为平箔片后沿的循环气流温度,Tsuc为吸入冷却空气的温度,为室温T0;qrec为循环气流量,qsuc为吸入的冷却气体的流量.
计算得到的入口气膜温度Tin作为气膜能量方程的一个边界条件,带入到能量方程中进行求解,在圆周方向以向后差分的形式可以迭代求解循环温度值Trec,并将Trec作为气体混合模型的输入值,计算得到新的入口气膜温度Tin,完成一个耦合迭代过程.
1.4 转子热传递模型气膜内部产生的热量一部分传向转子,经转子孔壁传到内表面,经对流换热传出. 在这个过程中满足能量传递的连续性,由气膜传向转子的热流Qfilm→rotor与转子内表面换热量Qrotor_inner→cooling分别为
| $\begin{align} & {{Q}_{\text{film}\to \text{yotor}}}=\int\limits_{0}^{L}{\int\limits_{0}^{2\pi }{k\times \frac{1}{h}}}{{\left. \frac{\partial {{T}_{\text{a}}}}{\partial \bar{z}} \right|}_{\bar{z}=1}}r\text{d}\theta \text{d}y \\ & {{Q}_{\text{rotor}\_\text{inner}\to \text{cooling}}}=\int\limits_{0}^{L}{\int\limits_{0}^{2\pi }{{{k}_{\text{cond}\_\text{s}}}}}\times {{\left. \frac{\partial {{T}_{\text{s}}}}{\partial r} \right|}_{r={{R}_{\text{in}}}}}r\text{d}\theta \text{d}y= \\ & {{k}_{\text{cond}\_\text{s}}}\times {{\left. \frac{\partial {{T}_{\text{s}}}}{\partial r} \right|}_{r={{R}_{\text{in}}}}}\times L\times 2\pi \times {{R}_{\text{in}}}. \\ \end{align}$ |
式中:k为气膜导热系数,h为气膜厚度;L为轴承宽度,kcond_s为转子导热系数,Rin为转子内半径.
在模型耦合求解时,先给定较低的转子表面温度,以此作为边界条件计算气膜三维温度分布,同时可以得到转子的一维径向温度分布,则转子内外表面的总热流量可分别计算得到,将内外表面的热流差值作为总体迭代过程的收敛特征.
1.5 动态刚度与阻尼求解通过小扰动法数值求解非等温条件下的动态Reynolds方程
| $\begin{align} & \frac{1}{{{R}^{2}}}\frac{\partial }{\partial \theta }\left( \frac{p{{h}^{3}}}{12\mu T}\frac{\partial p}{\partial \theta } \right)+\frac{\partial }{\partial y}\left( \frac{p{{h}^{3}}}{12\mu T}\frac{\partial p}{\partial y} \right)= \\ & \frac{\omega }{2}\frac{\partial }{\partial \theta }\left( \frac{ph}{T} \right)+\frac{\partial }{\partial \text{t}}\left( \frac{ph}{T} \right) \\ \end{align}$ |
可以计算出轴承的动态刚度与阻尼系数. 在转子的平衡位置产生的微扰动位移模式为
| $\Delta X=\Delta x/C=|\Delta X|{{e}^{\text{ivt}}}\Delta Y=\Delta y/C=|\Delta Y|{{e}^{\text{ivt}}}.$ |
其中:v为涡动频率;γ为v与转子角速度ω的比值,简称涡动比,γ=v/ω. 当转子受到外界扰动时,动态载荷也可以在平衡位置基于扰动位移与扰动速度按照泰勒公式展开:
| $\vec{F}={{{\vec{F}}}_{0}}+\frac{\partial \vec{F}}{\partial x}\Delta x+\frac{\partial \vec{F}}{\partial \dot{x}}\Delta \dot{x}+\frac{\partial \vec{F}}{\partial y}\Delta y+\frac{\partial \vec{F}}{\partial \dot{y}}\Delta \dot{y},$ |
则动态刚度与阻尼系数可以定义为
| $\begin{array}{l} \left\{ \begin{array}{l} {K_{xx}} = \partial {{\vec F}_x}/\partial x,\\ {K_{yx}} = \partial {{\vec F}_x}_y/\partial x; \end{array} \right.\left\{ \begin{array}{l} {K_{xy}} = \partial {{\vec F}_x}/\partial y,\\ {K_{yy}} = \partial {{\vec F}_y}/\partial y; \end{array} \right.\\ \left\{ \begin{array}{l} {D_{xx}} = \partial {{\vec F}_x}/\partial \dot x,\\ {D_{yx}} = \partial {{\vec F}_y}/\partial \dot x; \end{array} \right.\left\{ \begin{array}{l} {D_{xy}} = \partial {{\vec F}_x}/\partial \dot y,\\ {D_{yy}} = \partial {{\vec F}_y}/\partial \dot y. \end{array} \right. \end{array}$ |
为了证明理论模型与编程的正确性,将计算结果与文献[15]中的实验结果进行对比,文献[15]中的轴承的结构参数、运行参数与气体属性参数见表 1、2.
| 表 1 计算初始参数 Table 1 Initial calculating parameters |
| 表 2 波箔轴承结构参数 Table 2 Structural parameters of the bump foil bearing |
程序计算流程图如图 4所示,先进行等温条件下气弹耦合解,并根据计算的气膜压力、厚度通过能量方程计算气膜温度分布,根据计算的气膜温度更新气膜厚度与轴承结构特性参数、气膜特性参数,并在此基础上求解非等温条件下的Reynolds方程. 按照这种迭代求解方式,最终能够得到收敛的气膜压力、气膜厚度分布与气膜温度分布.

|
图 4 程序计算流程图 Figure 4 Flow chart of the calculating program |
采用表 1、2中的初始参数,计算轴承转速为2.0×104 ~5.0×104 r/min,不同载荷条件下的轴承峰值温度,理论计算值与文献中的实验数据对比结果如图 5所示.

|
图 5 不同转速与载荷下气膜峰值温度计算值与文献[15]对比 Figure 5 Theoretical and experimental peak film temperatures under different bearing load and speed conditions |
从图 5中可以看出,理论计算结果与文献数据有一定差距,实验数据的气膜峰值温度更容易受轴承载荷的影响,理论结果的气膜峰值温度随着载荷增加也有一定程度的增加,但变化趋势不明显. 理论与实验结果都反应出轴承转速是影响气膜温度的主要因素,不同转速时,理论计算结果的温度值与实验数据接近,一定程度上验证了模型的准确性.
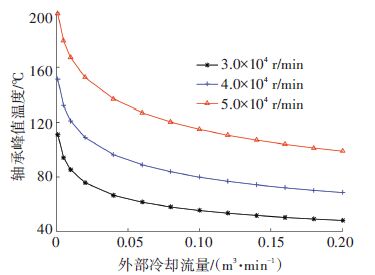
2.4 轴承温度的影响因素分析从图 5中可看出,转速变化对轴承温度有较大影响,载荷变化的影响较小. 图 6为相同载荷、不同转速条件下,外部冷却气流对轴承温度的影响情况. 从图 6中可看出,外部冷却气流对轴承温度有较大的影响. 当冷却气流流量从0增大到0.2 m3/min时,轴承峰值温度下降了1半. 但同时也可以发现,冷却气流的冷却效率随着流量的增大逐渐降低.
|
中文注解 图 6 轴承峰值温度随外部冷却流量的变化趋势 Figure 6 Bearing peak temperature changing with external cooling flux |
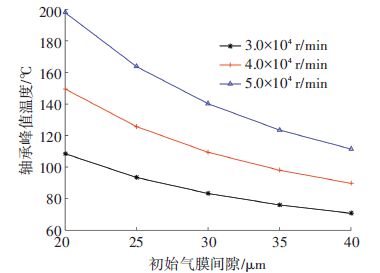
图 7描述了相同载荷、不同转速条件下,轴承初始气膜间隙对气膜温度的影响. 从图 7中可看出,初始气膜间隙对于轴承温度有较大影响,尤其是在高转速情况下,随着间隙值减小,轴承温度有更显著升值. 因此对于高转速工作条件的轴承,温度控制与装配间隙的选取应该得到足够重视.
|
图 7 轴承峰值温度随初始气膜间隙的变化趋势 Figure 7 Bearing peak temperature changing with initial normal clearance |
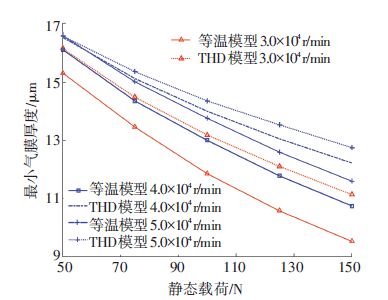
图 8为不同转速条件下,分析采用等温模型与THD模型时,波箔轴承最小气膜厚度随静态载荷的变化趋势. 从图 8中可以看出,对于等温模型或THD模型,最小气膜厚度相同时,较高的转速能够获得较大的承载能力,这是由于气膜在高转速时具有更强的流体动压效应. 同时,相同转速、最小气膜厚度条件下,THD模型预测的轴承承载力较大,这是因为非等温条件下气膜黏度会随着温度升高而增大,而且轴承结构热膨胀会减小初始气膜间隙,起到预紧作用,从而增大了气膜的动压效应.
|
图 8 等温模型与THD模型最小气膜厚度随载荷变化趋势 Figure 8 Minimal film thickness changing with bearing load at different rotor speed |
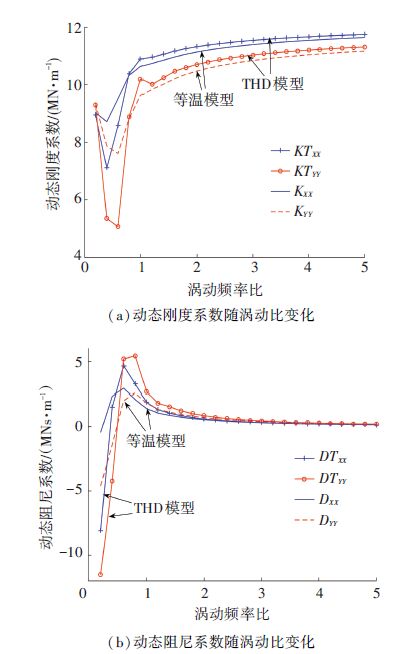
图 9(a)对比分析了轴承转速为5.0×104 r/min,转子偏心为10 μm时,等温模型与THD模型的主动态刚度系数Kxx与Kyy随涡动频率比γ的变化趋势. 从该图中可以看出,x与y方向的动态刚度系数直接项均随γ的增大呈先减小后增大的变化趋势,在γ为0.5附近存在最小值; 当γ>1时,刚度系数的变化趋势变缓. 理论上载荷方向y的动刚度较大,但当偏心较小,非载荷方向具有较大刚度. 当γ<0.5时,THD模型的动刚度较小; 反之,THD模型计算理论值较大.
|
图 9 动态刚度与阻尼随涡动频率的变化关系 Figure 9 Dynamic stiffness and damping coefficients changing with the rotor whirl ratio |
图 9(b)对比分析了相同条件下,动态阻尼系数Dxx与Dyy随γ的变化趋势. 可以看出,x与y方向的动态阻尼系数直接项均随γ的增大呈先增大后减小的变化趋势,在γ为0.5附近存在最大值; 当γ>1时,阻尼系数的变化趋势变小. 载荷方向y的动阻尼较大,当γ<0.5时,THD模型的动阻尼较小; γ>0.5时,THD模型计算理论值较大.
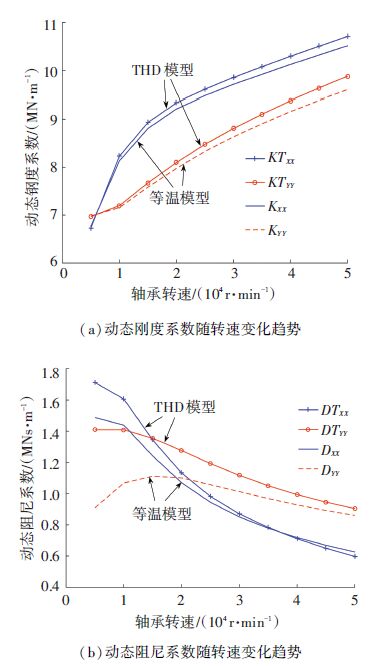
图 10 (a),(b)为给定载荷为50 N、γ为2条件下,动态刚度与阻尼系数随转速的变化趋势. 从图 10可看出,随着转速增加,动态阻尼总体上逐渐减小,动态刚度逐渐增大. 除了载荷方向的主阻尼外,当转速较高时,THD模型计算的动态刚度与阻尼系数较大.
|
图 10 动态刚度与阻尼随转速的变化关系 Figure 10 Dynamic stiffness and damping coefficients changing with the rotor speed |
1) 建立了波箔气体动压轴承的能量传递模型,包括润滑气膜的三维能量传递模型,箔片结构的热传导与对流换热模型,转子与轴承套的径向导热模型.
2) 推导了平箔片内表面的等效对流换热系数,耦合求解了气膜的能量方程、Reynolds方程、气膜厚度方程,得到了气膜温度三维温度分布,轴承结构的温度分布.
3) 通过理论计算结果与文献中实验数据的对比,验证了模型与程序的准确性.
4) 分析了轴承转速、静态载荷、外部冷却流量、初始气膜间隙对轴承温度的影响. 计算结果表明: 载荷对轴承温度影响不大,转速是影响轴承温度的主要因素,波箔通道中通入冷却空气能够有效降低轴承温度,冷却效率随着冷却流量的增大而逐渐降低,初始气膜间隙对于轴承峰值温度有重要影响. 对比分析了等温模型与THD模型的最小气膜厚度随承载力的变化趋势,以及转速与涡动频率比对动态刚度、阻尼的影响.
| [1] | HESHMAT H. Advancements in the performance of aerodynamic foil journal bearings: high speed and load capability[J]. Journal of tribology, 1994, 116 (2) : 287-294. DOI: 10.1115/1.2927211 |
| [2] | AGRAWAL G L. Foil air/gas bearing technology: an overview[C]//ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition.: American Society of Mechanical Engineers, 1997: V001T04A006-V001T04A006. DOI: 10.1115/97-GT-347. |
| [3] | DELLACORTE C, VALCO M J. Load capacity estimation of foil air journal bearings for oil-free turbomachinery applications[J]. Tribology Transactions, 2000, 43 (4) : 795-801. DOI: 10.1080/10402000008982410 |
| [4] | KIM D, KI J. Extended three-dimensional thermo-hydrodynamic model of radial foil bearing: case studies on thermal behaviors and dynamic characteristics in gas turbine simulator[J]. Journal of Engineering for Gas Turbines and Power, 2012, 134 (5) : 052501(1-13). DOI: 10.1115/1.4005215 |
| [5] | KIM T H, LEE Y B, KIM T Y, et al. Rotordynamic performance of an oil-free turbo blower focusing on load capacity of gas foil thrust bearings[J]. Journal of Engineering for Gas Turbines and Power, 2012, 134 (2) : 022501(1-7). DOI: 10.1115/1.4004143 |
| [6] | DYKAS B, BRUCKNER R, DELLACORTE C, et al. Design, fabrication, and performance of foil gas thrust bearings for micro turbomachinery applications[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131 (1) : 012301(1-8). DOI: 10.1115/1.2966418 |
| [7] | DYKAS B, HOWARD S A. Journal design considerations for turbomachine shafts supported on foil air bearings[J]. Tribology Transactions, 2004, 47 (4) : 508-516. DOI: 10.1080/05698190490493391 |
| [8] | HOWARD S, DELLACORTE C, VALCO M J, et al. Dynamic stiffness and damping characteristics of a high-temperature air foil journal bearing[J]. Tribology transactions, 2001, 44 (4) : 657-663. DOI: 10.1080/10402000108982507 |
| [9] | SALEHI M, SWANSON E, HESHMAT H. Thermal features of compliant foil bearings: theory and experiments[J]. Journal of Tribology, 2001, 123 (3) : 566-571. DOI: 10.1115/1.1308038 |
| [10] | PENG Z C, KHONSARI M M. A thermohydrodynamic analysis of foil journal bearings[J]. Journal of tribology, 2006, 128 (3) : 534-541. DOI: 10.1115/1.2197526 |
| [11] | LEE D, KIM D. Thermohydrodynamic analyses of bump air foil bearings with detailed thermal model of foil structures and rotor[J]. Journal of Tribology, 2010, 132 (2) : 021704(1-12). DOI: 10.1115/1.4001014 |
| [12] | FENG K, KANEKO S. A thermohydrodynamic sparse mesh model of bump-type foil bearings[J]. Journal of Engineering for Gas Turbines and Power, 2013, 135 (2) : 022501(1-12). DOI: 10.1115/1.4007728 |
| [13] | ANDRS L S, KIM T H. Thermohydrodynamic analysis of bump type gas foil bearings: a model anchored totest data[J]. Journal of Engineering for Gas Turbines and Power, 2010, 132 (4) : 042504(1-10). DOI: 10.1115/1.3159386 |
| [14] | DELLACORTE C. A new foil air bearing test rig for use to 700 c and 70,000 rpm[J]. Tribology transactions, 1998, 41 (3) : 335-340. DOI: 10.1080/10402009808983756 |
| [15] | RADIL K, ZESZOTEK M. An experimental investigation into the temperature profile of a compliant foil air bearing[J]. Tribology transactions, 2004, 47 (4) : 470-479. DOI: 10.1080/05698190490501995 |
| [16] | HOLMAN J P. Heat Transfer[M]. 北京: 机械工业出版社, 2011 : 191 -193. |
 2017, Vol. 49
2017, Vol. 49


