电液负载模拟器是一种半实物仿真设备,其功能是模拟飞机、导弹等在飞行过程中舵机所受各种空气动力的力/力矩载荷,从而在地面检测舵机驱动系统的技术性能指标[1]. 使用电液负载模拟器,可将自破坏的全实物实验转化为在实验室条件下的半实物预测性实验,以达到缩短舵机研制周期、节约研制经费、提高可靠性和成功率的目的[2-3]. 传统电液负载模拟器与被测舵机系统是近似刚性地连接在一起. 当被测舵机主动运动时,必然对负载模拟器产生强扰动,该扰动即所谓的“多余力矩”,其数值与舵机的运动状态有关,在起动、换向和高频运动时更为严重[4]. 由于多余力矩的存在及不可避免,使得电液负载模拟器很难获得高精度、宽频带的力矩加载性能. 尤其是在进行小幅值力矩加载时,多余力矩甚至会淹没加载信号,使系统无法实现正常的小幅值加载.
为了抑制多余力矩,在结构上,王经甫、张彪等[5-6]提出了双阀流量补偿控制法,Cui等[7]提出了基于压力伺服阀来抑制多余力矩,哈工大流体教研室引入了一个位置同步补偿马达来补偿多余力矩[8]. 在控制策略上,张彪等[9]提出了基于反步的全状态反馈控制,Truong等[10]提出了一种自校正灰色预测-模糊PID控制,李阁强等[11]提出了一种鲁棒控制策略,Li等[12]提出了一种解耦控制,Yoonsu等[13]提出了定量反馈控制. 总体来说,所提出的这些方法只能在一定程度上抑制多余力矩,传统电液负载模拟器无法满足日益提高的力矩加载性能要求.
为了彻底消除多余力矩,全面提高力矩加载性能,本文提出了一种摩擦加载式力矩加载结构. 通过力矩加载实验研究来验证所提方法的可行性,同时为进一步优化该加载结构以及提高力矩加载性能提供实验基础.
1 单向摩擦加载式电液负载模拟器由于是实验验证研究,为了节省成本,首先研究单向摩擦加载式力矩加载的可行性. 由于液压伺服系统较电机伺服系统及气动伺服系统具有高精度、快速响应、强抗干扰性及大的功率-质量比等优点[14],本文研究单向摩擦加载式电液伺服力矩加载,其加载原理如图 1所示[15].
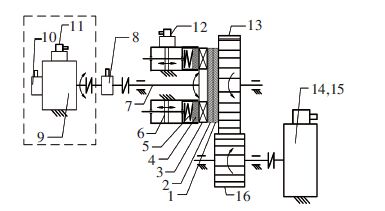
|
1—恒动摩擦盘;2—摆动摩擦盘;3—止推轴承;4—过渡板;5—弹簧;6—液压缸;7—主轴;8—扭矩传感器;9—液压马达;10—光电编码器;11—大伺服阀;12—小伺服阀;13—大齿轮;14,15—电机及减速器;16—小齿轮 图 1 单向摩擦加载式电液伺服力矩加载原理 Figure 1 Schematic diagram of the single-way friction based electrohydraulic load simulator |
如图 1所示,恒动摩擦盘固定在大齿轮的侧面,电机及减速器通过小齿轮驱动大齿轮及恒动摩擦盘在主轴上按一个方向恒速转动,摆动摩擦盘通过滑键与主轴连接,小伺服阀驱动3个周向均布并固定在基座上的液压缸,3个液压缸通过弹簧、过渡板及止推轴承向摆动摩擦盘施加压力. 图 1虚线框中的为被测舵机系统,主要由大伺服阀驱动液压马达摆动组成,光电编码器用来测量马达摆动角位移,液压马达轴通过扭矩传感器与主轴刚性连接,因此,摆动摩擦盘将同液压马达一同进行摆动. 扭矩传感器用来测量主轴所受的扭矩即两摩擦盘间产生的摩擦力矩. 由于恒动摩擦盘转速高于液压马达的最大摆动速度,则两摩擦盘间始终有一个恒定方向的相对转动,因此液压缸施加到两摩擦盘间的压力将被转化为摩擦力矩. 同时摩擦力矩将通过摆动摩擦盘、滑键、主轴及扭矩传感器作用于液压马达,从而实现对被测舵机的负载模拟. 由于利用了止推轴承及滑键,同时两摩擦盘间有恒方向相对转动,忽略止推轴承的转动摩擦力及滑键与摆动摩擦盘间的静摩擦力,因此理论上所设计的摩擦加载式负载模拟加载性能不受舵机摆动干扰,即无多余力矩.
图 1所示的加载结构只能模拟正力矩或负力矩. 为了既能模拟正力矩又能模拟负力矩,在液压缸左侧再对称布置一套液压缸右侧的两个齿轮、两个摩擦盘、止推轴承、弹簧及过渡板等结构,同时设计合理的传动装置,使得液压缸两侧的大齿轮转动方向相反但转速相同. 这种双向摩擦加载式电液负载模拟器与单向的在加载原理及关键技术上相似,将在以后的工作中进行研究.
为了实验验证该摩擦加载式力矩加载方法无多余力矩,并能获得高性能的力矩加载结果,根据图 1所示的加载原理,搭建了单向摩擦加载式电液负载模拟器实验样机,如图 2所示.

|
图 2 试验样机 Figure 2 Experimental prototype |
该单向摩擦加载式电液负载模拟器样机主要包括1台中航609所研制的FF101-8电液伺服阀,1台北京威斯特中航生产的CYB802S静态扭矩传感器,3个自行设计的液压缸,3个矩形弹簧,1对自行设计的恒动摩擦盘和摆动摩擦盘,1个标准的止推轴承,1台标准电机及1台标准减速器等. 系统硬件主要包括1块研华PCI1716 D/A卡,1块研华PCI1710 A/D卡,1台研华IPC610H工控机及两块朝阳电源等. 系统控制软件为1套在VC++6.0环境下基于Windows+Ardence RTX平台自行开发的实时控制软件,其定时周期设定为0.2 ms. 被测舵机系统主要由1台中航609所研制的FF106电液伺服阀、1台自行设计的摆动液压马达及1台长春光机所研制的编码器组成. 系统供油压力11 MPa.
2 控制数学模型为了实现对摩擦力矩的精确控制,需要建立并分析该单向摩擦加载式电液负载模拟器的数学模型. 如图 1所示,该负载模拟器的动力机构为流量伺服阀同时控制3个相同的对称液压缸,为了简化分析,3个液压缸可以等效成1个液压缸,3个弹簧可以等效成1个弹簧. 因此该数学模型可以按阀控对称缸模型来建立[14].
假定阀为理想四通滑阀,且节流窗口是匹配对称的,阀的线性化流量方程[14]可以写为
| ${Q_{\rm{L}}} = {K_{\rm{q}}}{X_{\rm{v}}} - {K_{\rm{c}}}{p_{\rm{L}}}.$ | (1) |
式中:QL为阀的负载流量,Kq为阀的流量增益,Xv为阀芯的开口量,Kc为阀的流量-压力系数,pL为加载液压缸的负载压力.
忽略阀内液体压缩性的影响,等效液压缸流量连续性方程[14]可以写为
| ${Q_{\rm{L}}} = {A_{\rm{p}}}s{X_{\rm{p}}} + {C_{{\rm{tp}}}}{p_{\rm{L}}} + \frac{{{V_{\rm{t}}}}}{{4{\beta _{\rm{e}}}}}s{p_{\rm{L}}}.$ | (2) |
式中:Ap为加载等效液压缸活塞有效面积,Xp为等效液压缸的位移,Ctp为等效液压缸的总泄漏系数,Vt为加载系统总的有效容积,βe为有效体积弹性模数.
由于作用在等效液压缸上的负载主要是等效弹簧的弹性负载,忽略惯性负载、库仑摩擦等非线性和黏性阻尼等,可得力平衡方程[14]为
| ${A_{\rm{p}}}{P_{\rm{L}}} = K{X_{\rm{p}}}.$ | (3) |
式中K为等效弹簧的刚度.
电液伺服阀的动态用以下环节近似表示[14]:
| ${G_{{\rm{sv}}}}\left( s \right) = \frac{{{X_{\rm{v}}}\left( s \right)}}{{I\left( s \right)}} = \frac{{{K_{{\rm{sv}}}}/{K_{\rm{q}}}}}{{\frac{{{s^2}}}{{{\omega ^2}_{{\rm{sv}}}}} + \frac{{2{\xi _{{\rm{sv}}}}}}{{{\omega _{{\rm{sv}}}}}}s + 1}}.$ | (4) |
式中:I为输入电流,Ksv为伺服阀增益,ωsv为伺服阀的固有频率,ξsv为伺服阀的阻尼比.
假设两摩擦盘间的摩擦系数恒定,液压缸施加的力均匀作用于两摩擦盘接触面上,容易得到
| $T = {K_{\rm{t}}}K{X_{\rm{p}}}.$ | (5) |
式中:Kt为摩擦盘力-力矩转化系数,T为输出力矩.
记伺服放大器增益为Ka=I(s)/U(s).由式(1)~(5),根据前面所述的摩擦加载式力矩加载工作原理可得该负载模拟器的线性三阶开环传递函数为
| $\frac{{{K}_{\text{a}}}{{K}_{\text{sv}}}{{A}_{\text{p}}}K{{K}_{\text{t}}}}{(\frac{{{s}^{2}}}{\omega _{\text{sv}}^{2}}+\frac{2{{\xi }_{\text{sv}}}}{{{\omega }_{\text{sv}}}}s+1)[(A_{\text{p}}^{2}+\frac{{{V}_{\text{t}}}K}{4{{\beta }_{\text{e}}}})s+{{K}_{\text{c}}}K+{{C}_{\text{tp}}}K]}.$ | (6) |
式中U为控制电压.
如前所述,被测舵机系统的主运动对加载系统没有干扰作用,但为了验证该负载模拟器无多余力矩,需要被测舵机系统在实验中向该负载模拟器提供摆动干扰. 舵机系统数学模型可参见文献[14].
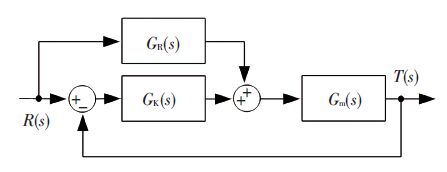
3 控制器设计本文的主要目的在于验证该单向摩擦加载式电液负载模拟器在结构上没有多余力矩,并能获得高性能的力矩加载结果. 因此,为了充分证明该加载方法在结构上的优越性,本文不对系统的不确定性、外界干扰及噪声等进行任何控制策略上的补偿以提高加载性能,主要采用工业上运用最为广泛的PID控制器. 但是,PID控制器在实际运用中只能在低频范围内获得较高精度的控制效果,在非低频范围内则会有较大的相位滞后及幅值衰减,不能满足控制性能的要求. 由于负载模拟器一般要求较高的频率响应,为了进一步验证该摩擦加载式电液负载模拟器优于传统电液负载模拟器,本文的力矩加载实验研究需要在非低频范围内进行. 为了提高PID控制器在非低频范围的控制性能,根据第2节所建立的控制数学模型,在PID控制器基础上引入前馈控制器. PID控制器能够获得基本的性能,前馈控制器能够提高系统的跟踪速度与跟踪精度. 图 3所示为PID+前馈控制的单向摩擦加载式电液负载模拟控制框图.
|
图 3 控制框图 Figure 3 Control block diagram |
如图 3所示,Gm(s)为如式(6)所示的被控负载模拟器传递函数,GK(s)为PID控制器,GR(s)为前馈控制器,R(s)为系统期望输入,T(s)为系统输出.
由图 3可得系统的控制误差传递函数
| $E\left( s \right) = T\left( s \right) - R\left( s \right) = \frac{{{G_{\rm{R}}}\left( s \right){G_{\rm{m}}}\left( s \right)R\left( s \right) - R\left( s \right)}}{{1 + {G_{\rm{K}}}\left( s \right){G_{\rm{m}}}\left( s \right)}}.$ |
若使系统控制误差为零,需要前馈控制器满足
| ${G_{\rm{R}}}\left( s \right) = \frac{1}{{{G_{\rm{m}}}\left( s \right)}}.$ |
由式(6)可知
| ${G_{\rm{R}}}\left( s \right) = {a_{\rm{f}}} + {b_{\rm{f}}}s + {c_{\rm{f}}}{s^2} + {d_{\rm{f}}}{s^3}.$ | (7) |
式中:${a_{\rm{f}}} = \frac{{{K_{\rm{c}}}K + {C_{{\rm{tp}}}}K}}{{{K_{\rm{L}}}}}$,
| $\begin{array}{l} {b_{\rm{f}}} = \frac{{2{\xi _{{\rm{sv}}}}({K_{\rm{c}}}K + {C_{{\rm{tp}}}}K)}}{{{K_{\rm{L}}}{\omega _{{\rm{sv}}}}}} + \frac{{A_{\rm{p}}^2}}{{{K_{\rm{L}}}}} + \frac{{{V_{\rm{t}}}K}}{{4{\beta _{\rm{e}}}{K_{\rm{L}}}}}\\ {c_{\rm{f}}} = \frac{{{K_{\rm{c}}}K + {C_{{\rm{tp}}}}K}}{{\omega _{{\rm{sv}}}^2{K_{\rm{L}}}}} + \frac{{8{\beta _{\rm{e}}}{\xi _{{\rm{sv}}}}A_{\rm{p}}^2 + {V_{\rm{t}}}K{\omega _{{\rm{sv}}}}}}{{4{\beta _{\rm{e}}}{\omega _{{\rm{sv}}}}{K_{\rm{L}}}}}\\ {d_{\rm{f}}} = \frac{{4{\beta _{\rm{e}}}A_{\rm{p}}^2 + {V_{\rm{t}}}K}}{{4{\beta _{\rm{e}}}\omega _{{\rm{sv}}}^2{K_{\rm{L}}}}}{K_{\rm{L}}} = {K_{\rm{a}}}{K_{{\rm{sv}}}}{A_{\rm{p}}}K{K_{\rm{t}}}. \end{array}$ |
式(7)所示的前馈控制器包含二阶和三阶等高阶微分环节. 由于实际应用中高阶微分环节容易放大系统测量噪声且不易实现,实际设计时可用比例环节和一阶微分环节之和近似获得式(7)的前馈控制器,即取式(7)中的cf和df为0,从而使被控系统控制误差趋于零.
PID控制器可表示为
| ${{G}_{K}}\left( s \right)={{K}_{\text{a}}}+{{K}_{\text{I}}}\frac{1}{s}+{{K}_{\text{D}}}s.$ |
式中:Ka为比例可调参数,KI为积分可调参数,KD为微分可调参数.
4 实验 4.1 实验设计如第1节中所述,当被测舵机静止时,该单向电液负载模拟器与一般的阀控对称缸系统的主要区别在于,前者具有弹性负载同时具有一个力-力矩转化环节. 为了研究弹性负载和力-力矩转化环节等对该负载模拟器加载性能的影响,分别进行如下力矩加载实验: 1). 弹簧刚度对力矩跟踪性能影响,此时,其他条件相同,改变图 1中弹簧的刚度,在不同刚度下测试力矩加载性能. 2).摩擦盘性能对力矩跟踪性能影响,此时,其他条件相同,改变图 1中两摩擦盘的材料,在选用不同摩擦盘材料时测试力矩加载性能. 由于多余力矩的干扰,传统电液负载模拟器很难实现高性能的小幅值力矩加载[4],现有的文献中很少有小幅值加载研究. 由于理论上该摩擦加载式电液负载模拟器无多余力矩,考虑到假如有多余力矩,该负载模拟器将无法进行小幅值力矩加载,因此将进行如下力矩加载实验,即3). 小幅值力矩跟踪性能研究,此时,当舵机进行强烈摆动时,分别测试该负载模拟器跟踪不同小幅值期望力矩的跟踪性能. 为了验证该摩擦加载式电液负载模拟器小幅值加载性能的优势,可以对比现有的传统电液负载模拟器力矩加载结果[4]. 所有实验条件下,控制器的性能都调式到性能最优状态.
4.2 实验结果及分析 4.2.1 弹簧刚度对力矩跟踪性能影响当图 1中两摩擦盘材料均为一种复合材料时,图 4给出了分别采用刚度为6.5×105、1.2×105 N/m的弹簧,该负载模拟器跟踪频率5 Hz、幅值8 N·m、偏移15 N·m的正弦期望力矩的跟踪结果.

|
图 4 不同弹簧刚度下力矩跟踪结果 Figure 4 Torque tracking results under different spring stiffness |
由图 4可知,当采用大、小刚度弹簧时,系统的最大力矩跟踪误差分别为1.2和4.6 N·m. 实验结果表明,弹簧刚度对该负载模拟器的加载性能影响很大,需要结合仿真及实验选择刚度最优的弹簧来提高系统加载性能. 仿真结果表明,针对该负载模拟器样机的机械尺寸及标准弹簧的规格等,本样机的最优弹簧刚度应在6.5×105 N/m左右.
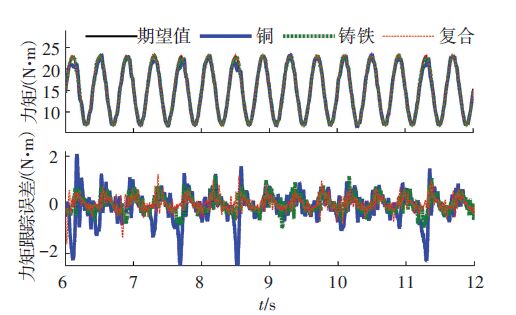
4.2.2 摩擦盘性能对力矩跟踪性能影响当弹簧刚度为最优的6.5×105 N/m时,图 5给出了当两个摩擦盘材料分别都采用铸铁,都采用黄铜和都采用一种复合材料,该负载模拟器跟踪频率5 Hz、幅值8 N·m、偏移15 N·m的正弦期望力矩的跟踪结果.
|
图 5 不同摩擦材料下力矩跟踪结果 Figure 5 Torque tracking results under different friction materials |
由图 5可知,当两摩擦盘材料都为一种复合材料时,该负载模拟器最大力矩跟踪误差约为1.1 N·m. 当两摩擦盘材料都为铸铁时,最大跟踪误差约为1.2 N·m; 当两摩擦盘材料都为黄铜时,最大跟踪误差约为2.4 N·m. 总体可以看出:黄铜的力矩加载稳定性能差且加载精度最低;铸铁的加载稳定性较好且加载精度较高,但是铸铁容易磨损,需经常替换新的摩擦盘; 复合材料加载稳定性最好且加载精度最高,此外,所用的复合材料抗磨损能力强,能进行长时间的力矩加载,但是其价格较贵. 实验结果表明,摩擦盘的摩擦材料对该负载模拟器的加载性能有很大影响,为了获得更好的加载性能,可以采用摩擦系数稳定性更好,抗磨损能力更强的陶瓷、碳纤维等摩擦材料设计该负载模拟器的摩擦盘.
4.2.3 小幅值力矩跟踪性能研究根据前述实验结果,试验中两个摩擦盘材料均采用一种复合材料,同时采用弹簧刚度为6.5×105 N/m的弹簧. 为了充分模拟负载模拟器在实际工作中遭受的强干扰,实验中被测舵机做幅值10°,频率为8 Hz的正弦摆动. 图 6(a)~(c)分别给出了该电液负载模拟器跟踪幅值6 N·m、偏移10 N·m;幅值3 N·m、偏移6 N·m和幅值2 N·m、偏移8 N·m的正弦期望力矩的跟踪结果. 3种期望力矩频率均为5 Hz.
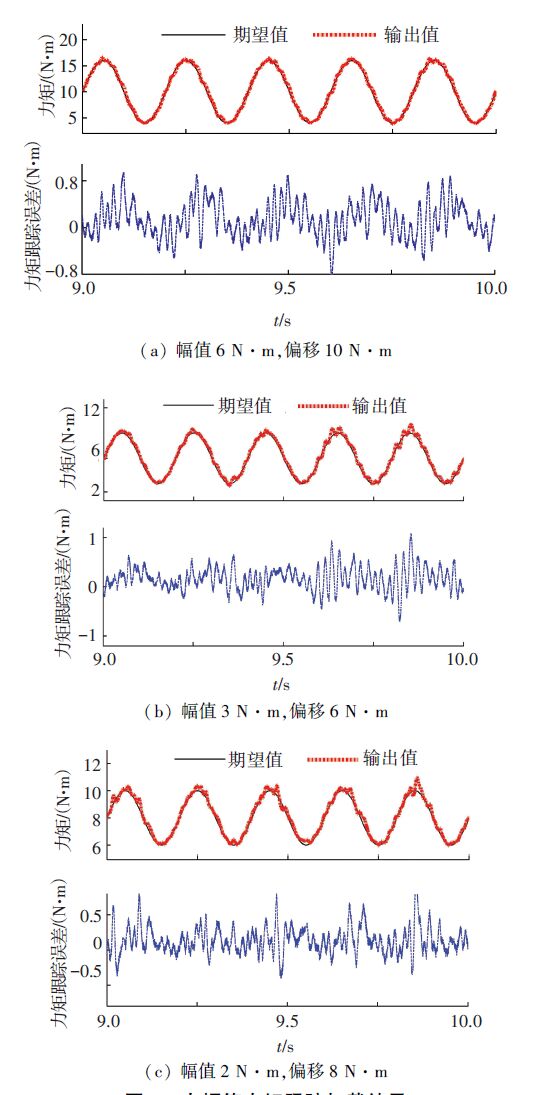
|
图 6 小幅值力矩跟踪加载结果 Figure 6 Small amplitude torque tracking results |
由图 6(a)~(c)可知,3种期望力矩的最大跟踪误差分别为0.9、1.1和0.9 N·m. 在被测舵机进行剧烈摆动干扰的情况下,该负载模拟器能够精确的跟踪3种不同小幅值的期望力矩,且其跟踪稳定好. 考虑到传统的电液负载模拟由于多余力矩的存在,图 6中3种小幅值期望力矩将被多余力矩淹没而无法实现力矩跟踪,因此图 6所示的精确力矩跟踪结果表明被测舵机的摆动对该摩擦加载式电液负载模拟器的力矩跟踪性能没有影响,即该负载模拟器没有多余力矩.
由图 6可知,该负载模拟器的小幅值力矩跟踪结果有较大的波动. 这主要由于该系统自身的非线性、参数不确定性及测量噪声等引起的. 当该负载模拟器在结构设计合理的情况下,上述因素可以通过相应的控制策略来进行补偿[16-17],从而可以进一步提高该负载模拟器的力矩跟踪性能.
5 结 论1) 弹簧及摩擦副等对摩擦加载式电液负载模拟器的加载性能有很大影响,为了获得高性能的力矩加载性能,需要选择最优刚度的弹簧及高摩擦性能的摩擦盘摩擦材料.
2) 摩擦加载式电液负载模拟器在强舵机主运动干扰下能够获得高性能的小幅值力矩加载性能,从而验证了该负载模拟器无多余力矩,并能够获得较高的力矩加载性能.
3) 本文的研究为今后的高性能无多余力矩双向摩擦加载式电液负载的结构设计、优化及控制策略设计等提供了实验基础.
| [1] |
郝经佳. 电液负载仿真台综合性能的研究[D]. 哈尔滨: 哈尔滨工业大学, 2001.
HAO Jingjia. Comprehensive performance research of a electrohydraulic load simulator[D]. Harbin: Harbin Institute of Technology, 2001. |
| [2] | BASIC G. Hardware-in-the-loop simulation of mechanical loads for mechatronics system design[D]. Ottawa: University of Ottawa, 2003. |
| [3] | BASIC M. On hardware-in-the-loop simulation[C]//Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference. Seville: IEEE press, 2005: 3194-3198. DOI:10.1109/CDC.2005.1582653. |
| [4] |
张彪. 电液负载模拟器多余力矩抑制及其反步自适应控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
ZHANG Biao. Extra torque rejection and adaptive backstepping control of electro hydraulic load simulator[D]. Harbin: Harbin Institute of Technology,2009. |
| [5] |
王经甫, 叶正茂, 李洪人. 双阀并联控制在船舶舵机电液负载模拟器多余力抑制中的研究[J].
机械工程学报, 2005, 41 (4) : 229-233.
WANG Jingfu, YE Zhengmao, LI Hongren. Study on eliminating the superfluous force of marine electrohydraulic load simulator applied with dual-valve parallel connected control[J]. Chinese Journal of Mechanical Engineering, 2005, 41 (4) : 229-233. DOI: 10.3901/JME.2005.04.229 |
| [6] |
张彪, 赵克定, 李阁强. 双阀控制电液被动施力系统的研究[J].
液压与气动, 2007 (12) : 30-33.
ZHANG Biao, ZHAO Keding, LI Geqiang. Study of double servo-valve controlled electro-hydraulic passive load system[J]. Chinese Hydraulics and Pneumatics, 2007 (12) : 30-33. |
| [7] | CUI J M, ZHANG B, DONG Y L. A study on performance of electro-hydraulic load simulator based on pressure servo valve[C]//Proceedings of 2015 International Conference on Fluid Power and Mechatronics. Harbin: IEEE press, 2015: 505-509. DOI:10.1109/FPM.2015.7337170. |
| [8] |
苏东海, 吴盛林, 付兴武, 等. 利用基于同步补偿的角速度差值克服多余力矩[J].
哈尔滨工业大学学报, 2000, 32 (1) : 78-81.
SU Donghai, WU Shenglin, FU Xingwu, et al. Eliminating disturbance torque by angular velocity difference based on synchro-compensation[J]. Journal of Harbin Institute of Technology, 2000, 32 (1) : 78-81. |
| [9] |
张彪, 赵克定. 基于反步控制的被动力伺服系统的全状态反馈控制[J].
西安交通大学学报, 2008, 42 (1) : 82-86.
ZHANG Biao, ZHAO Keding. Total state feedback control on passive force control system based on backstepping theory[J]. Journal of Xi’an Jiaotong University, 2008, 42 (1) : 82-86. |
| [10] | TRUONG D Q, AHN K K. Force control for hydraulic load simulator using self-tuning grey predictor-fuzzy PID[J]. Mechatronics, 2009, 19 (2) : 233-246. DOI: 10.1016/j.mechatronics.2008.07.007 |
| [11] |
李阁强, 赵克定, 袁锐波, 等. μ理论在电液负载模拟器中的应用[J].
航空学报, 2007, 19 (2) : 233-246.
LI Geqiang, ZHAO Keding, YUAN Ruibo, et al. Application of μ theory in electrohydraulic load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2007, 19 (2) : 233-246. |
| [12] | LI G Q, YANG H Y, LI S C, et al. Research on decoupling control for electro-hydraulic load simulator[C]//Proceedings of the 2012 International Conference on Advanced Mechatronic Systems. Tokyo: IEEE press, 2012: 18-21. |
| [13] | YOONSU N. QFT force loop design for the aerodynamic load simulator[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37 (4) : 1384-1392. DOI: 10.1109/7.976973 |
| [14] | MERRITT H E. Hydraulic control systems[M]. New York: John Wiley & Sons Inc, 1967 . |
| [15] | ZHENG D K, XU H G. Adaptive backstepping flatness control based on an adaptive state observer for a torque tracking electrohydraulic system[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21 (5) : 2440-2452. DOI: 10.1109/TMECH.2015.251-3205 |
| [16] | KIM W, WON D, TOMIZUKA M. Flatness-based nonlinear control for position tracking of electrohydraulic systems[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20 (1) : 197-206. DOI: 10.1109/TMECH.2014.2310498 |
| [17] | MANDAL P, SARKAR B K, SAHA R, et al. GA-optimized fuzzy feed forward bias control of motion by a rugged electrohydraulic system[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20 (4) : 1734-1742. DOI: 10.1109/TMECH.2014.2352156 |
 2017, Vol. 49
2017, Vol. 49


