高速飞机等飞行器的红外性能是其综合性能的重要组成部分. 由于探测角度和波段的差异,相对于尾喷焰红外辐射,高速气动热导致的目标表面的红外辐射不可忽视[1]. 相对于飞行试验,数值模拟方法由于其成本优势和复杂问题的易实现性,在获取高速飞行器的红外热像的研究中得到了广泛应用. 一些学者针对目标的红外辐射形成和分布特征开展了理论分析和数值模拟. 如杜胜华等[2]分析了某空间飞行器的红外光谱特性;单勇等[3]计算了亚音速和超音速条件下导弹蒙皮的红外光谱辐射强度;刘立等[4]分析了光学头罩在超音速条件下的热红外特性. 这类研究通常不考虑探测系统的成像传输过程. 而对目标在光学系统中的成像,现有的研究大多不考虑探测器口径和焦距,采用单视点近似或小孔成像近似,通过反向蒙特卡罗(RMC)法模拟,跟踪从像面或视点发射的光线,分析表面的方向辐射强度. 如Coiro[5]采用RMC法分析了B737客机的红外光谱成像特性;Surzhikov[6]对热气团的方向光谱成像特性进行了RMC模拟计算;Ross等[7]利用RMC法分析了再入飞行器的红外热成像. 本文作者曾采用RMC方法对目标辐射到探测阵列的红外热像传输过程进行了一体化数值模拟,获得了目标在红外成像阵列平面的能流密度[8]. 该方法将目标有效辐射计算与其在红外光学系统中的成像过程模拟紧密地联系在一起,仿真效果好,但如果红外探测器的参数(焦距、孔径和探测方位等)发生变化,那么需要重新进行模拟计算,导致不必要的计算消耗.
为实现对目标表面红外热像特征和探测系统成像的快速预测评估,考虑到实际中的大多数红外目标表面在探测波段内可近似为漫射面,本文将目标红外成像过程分解为目标表面辐射的产生、空间传输与红外系统中的传输汇聚两个阶段,提出了计算目标红外热像的等效辐射-汇聚法. 在导出相应计算关系式的基础上,给出了该方法的模拟过程;并以SDM飞机模型为对象,得到并分析了不同探测角度下的红外热像;通过与RMC法的目标红外成像传输过程一体化数值模拟相比较,验证了该方法的可靠性和计算的高效率.
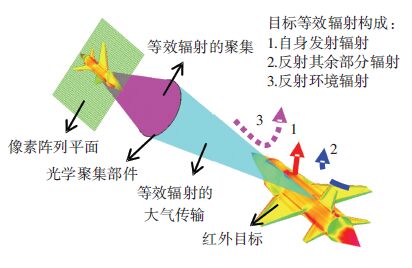
1 目标红外热像的等效辐射-汇聚法计算原理 1.1 目标表面等效辐射及其大气衰减的计算如图 1所示,目标在红外光学系统中的成像包含其自身等效辐射的形成、大气衰减及其在光学系统中的聚集成像两个物理过程. 目标表面的等效辐射,包含其自身辐射和对投入辐射的反射或散射. 对于飞机等高速飞行器而言,由于强烈的气动热效应,其表面的自身红外辐射强度远大于环境大气和地表的红外辐射;而太阳光主要集中在可见光波段[9],照射到飞行器表面的红外波段能量远小于目标自身的红外辐射. 为分析方便,对高速飞行目标表面某处的有效辐射主要考虑该处的自身辐射和对其它部位红外辐射的反射.
|
图 1 目标红外成像物理过程 Figure 1 Physical process of the infrared imaging of targets |
由于温度差异导致目标自身辐射与反射辐射的黑体光谱特性不一,考虑到大气吸收的强烈光谱性,所以二者之间以及反射辐射之间的大气衰减率不同. 为此,本研究将表面的自身辐射形成与其大气衰减过程作为一个整体进行考量.
真实气体的红外传输特性的计算主要包含谱带模型法[10]和逐线计算的方法[11]. 谱带模型方法采用了一定程度的近似,所以精度相对较低,但是逐线计算的方法的计算量相对较大. 为应用逐线计算方法,引入以下假设以降低其计算量:考虑到目标辐射的大气传输距离远大于目标的尺寸,因此可以忽略辐射在单元间相互反射中的衰减;同时光学系统入瞳面上不同点与目标的距离相差很小,所以目标上任意点辐射的大气衰减率对于固定的探测方位可认为是确定的数值.
考虑目标形状及温度、辐射物性的非均匀性,将目标表面划分为大量离散单元. 对某一离散单元i,其经过大气衰减的等效辐射强度为
| $I_i^e = {\tau _i}I_i^s + \sum\limits_{j = 1}^N {{\tau _j}I_{ji}^r} $ | (1) |
式中:N为离散单元的数目,τi和τj分别为单元i和单元j发射能量的大气透过率,Ijir为由单元j发射并被单元i反射的红外辐射强度,Iis=εiIi0为单元i自身红外辐射强度,εi为单元i的发射率,Ii0为单元i的黑体辐射强度.
考虑到表面反射能量与吸收能量的定量关系,Ijir可以表示为
| $I_{ji}^r = \frac{{(1 - {\varepsilon _i})}}{{{A_i}{\varepsilon _i}}}{A_j}{R_{ji}}I_j^s.$ | (2) |
式中:Rji为谱带内单元j对单元i的辐射传递因子,Ai和Aj分别为单元i和单元j的面积. 蒙特卡罗法采用光线随机抽样的方法计算单元间的辐射传递因子. 令某一单元i发射的随机光线的数量为Ni,跟踪每一条随机光线,统计系统内各个单元j吸收的份额Nij,那么单元i对单元j的辐射传递因子近似表示为
| ${{\tilde R}_{ij}} = {N_{ij}}/{N_i}.$ |
由式(2)和(1),Ijir和Iie的统计近似值可以表示为
| $\begin{gathered} \tilde I_{ji}^r = \frac{{\left( {1 - {\varepsilon _i}} \right)}}{{{A_i}{\varepsilon _i}}}{A_j}{{\tilde R}_{ji}}I_j^s, \hfill \\ {{\tilde I}^e}_i = {\tau _i}I_i^s + \sum\limits_{j = 1}^N {{\tau _j}\tilde I_{ji}^r} . \hfill \\ \end{gathered} $ | (3) |
当每个单元的抽样光线数为无穷大时,${{\tilde R}_{ji}}$的数值趋近于Rij. 然而实际单元发射的光线数都是有限的,所以${{\tilde R}_{ji}}$与Rij之间存在一定的统计偏差. 因为表面单元自身辐射Iis采用完全确定的方法进行计算,所以根据式(3)表面等效辐射的方差来源于反射辐射,进而来源于表面单元间的辐射传递因子,即
| $D({\tilde I^e}_i) = \sum\limits_{j = 1}^{{N_s}} {{{[\frac{{(1 - {\varepsilon _i})}}{{{A_i}{\varepsilon _i}}}{A_j}{\tau _j}I_j^s]}^2}D({{\tilde R}_{ji}})} .$ |
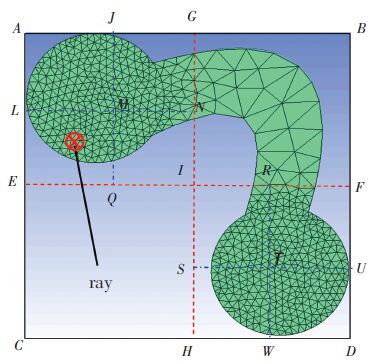
光线的随机发射点、发射方向和反射方向按参考文献[12]中的方法进行确定. 在传统方法中,光线与目标求交的计算最为耗时,因为上述计算要在光线与所有离散单元间进行. 对于实际目标,其表面的几何、物理量(温度、材料辐射物性等)的非均匀性都需要巨大的网格数量来分辨,所以上述时间消耗更为显著. 针对于此,本研究将目标的离散单元进行分组,而求交只在光线与特定分组里的单元进行,从而减少计算量. 具体采用八叉树自适应分区方法,八叉树的节点为长方体空间区域,每个节点可能包含8个子节点或不包含子节点,而节点是否继续分割取决于其包含单元的数量. 以图 2所示的二维情况为例进行说明,分区的过程包括创建根节点ABCD;一次分区将ABCD分为AGEI、GBIF、EICH和IFHD;二次分区将AGEI和IFHD进一步划分. 对于图中红色箭头所示的光线(垂直向内),其求交计算的过程为:光线依次与节点ABCD、AGEI、LMEQ的求交计算和其与叶节点LMEQ包含单元的求交计算.
|
图 2 目标八叉树自适应分区过程 Figure 2 Process of self-adaptive octree region grouping of target |
对于如图 1所示的经过大气衰减的表面等效辐射在红外光学系统中汇聚成像的计算,按以下步骤进行:确定目标上任意点的成像位置;计算成像位置汇聚的等效辐射能量.
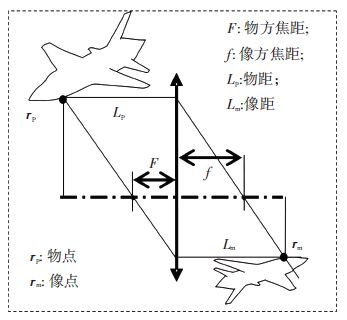
实际的成像系统可以等效为一个像方焦距与物方焦距不同的透镜,如图 3所示. 因此可以利用透镜的成像法则计算目标的成像位置. 对目标上的一点,如果其位置矢量为rp,经推导,其成像点的位置矢量rm可以表示为
| ${r_m} = \frac{{n \cdot ({r_0} - {r_p})[{r_0} + \left( {f - F} \right)n] - F{r_p}}}{{({r_0} - {r_p}) \cdot {\text{n}} - F}}.$ |
式中:F和f分别为物方和像方焦距,n为透镜平面的单位内法向量,r0为等效透镜的中心的位置矢量.
|
图 3 目标与成像系统 Figure 3 Targets and the optical imaging system |
利用光线穿越成像系统时的强度和方向变化规律可以得出像点汇聚的辐射照度. 经推导得出,从目标表面上的一点rp发出,被入瞳面S汇聚到点rm的单位面积的红外辐射能流密度Ei可以表示为
| ${E_i} = \iint\limits_S {\tau {I_i}^e\frac{{(r - {r_m}) \cdot n}}{{|r - {r_m}{|^3}}}ds}.$ |
式中:r为入瞳面S中的任一点的位置矢量,|r-rm|为r到像点rm的距离,τ为光学系统的透过率,Iie为点rp处经过大气衰减的红外目标表面的等效辐射强度.
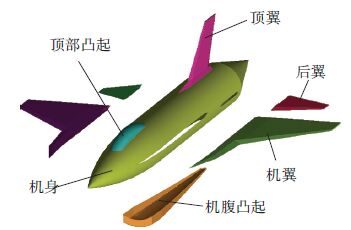
2 算例的几何与物理模型以图 4所示的SDM标准飞机模型为研究对象,该模型是一种三代机风动试验模型[13],其几何特征为:模型弦向总长0.3 m,共包含机身、上下凸起部分、机翼、后翼和顶翼几个部分,同时为减小尾部回流的影响,增加了一个锥形体结构. 本研究仅关注模型表面的红外特性,没有考虑尾喷焰对其整体红外成像特性的贡献.
|
图 4 SDM模型的几何结构 Figure 4 Configuration of the SDM model |
蒙皮温度是飞机红外图像计算的输入条件[14],其分布受到外部与机舱内热环境的共同作用. 本文关注点在目标的红外成像,所以仅考虑对温度具有显著影响的气动热. 以CFD软件ANSYS CFX作为工具对气动热进行模拟,计算的来流条件见表 1.
| 表 1 SDM模型的来流条件 Table 1 Incoming flow parameters for the SDM model |
大气中的H2O蒸汽和CO2对目标的红外辐射具有强烈的衰减作用,大气的光谱吸收参数利用HITRAN2008[15]光谱数据库进行计算. 大气的温度和压力对谱线的线形具有很大的影响,而HITRAN数据库仅提供了标准条件下的参数,所以非标准条件下的数值需要进行换算,具体可参见文献[16].
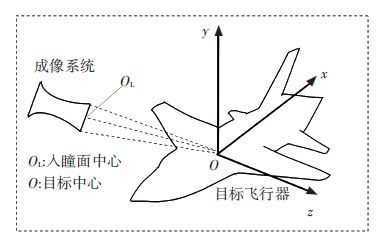
为表示目标和红外成像系统的位置关系,建立如图 5所示的全局坐标系. 成像系统的方位以飞机模型中心到入瞳面中心的距离和从目标中心到入瞳面中心的向量的分量形式表示.
|
图 5 目标表面笛卡尔坐标和成像系统方位 Figure 5 The Cartesian coordinates system of target and the azimuth of the optical image system |
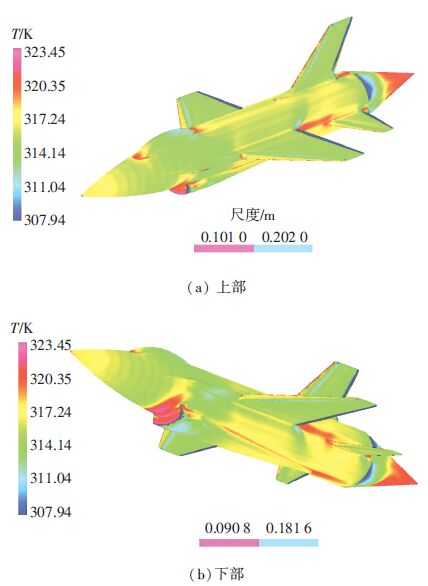
图 6为SDM标准模型的CFD模拟计算得到的温度分布云图. 从图 6中可以看出,机身上部和下部凸起部分的前方,由于气动压缩作用较为强烈,所以其表面温度显著地高于其他部分. 除此之外,在机身后部等回流较为强烈的部分,也存在高温区域.
|
图 6 SDM标准模型的温度分布 Figure 6 The temperature distribution on the SDM model |
以SDM模型温度分布作为基础,计算了8~14 μm波段模型的红外热像. 目标表面的离散单元数为243 578个,发射率为0.3,每个单元发射的光线数为104根. 在每个探测方位,探测器入瞳面中心点到目标几何中心点的距离均为103 m,入瞳面的内法向经过飞机模型的几何中心. 红外成像系统的其他参数如表 2所示.
| 表 2 红外成像系统的参数 Table 2 Parameters of the infrared image system |
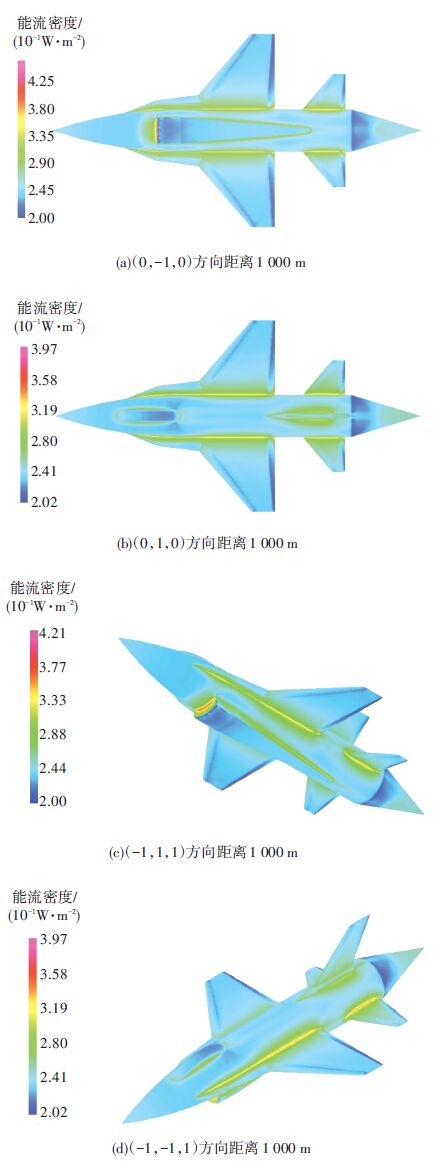
图 7为利用等效辐射-汇聚法计算的SDM飞机模型红外热像. 从图 7中可以看出,焦平面上的能流分布的变化较为连续. 在气动热和回流较强的区域,如上下部凸起物的前方和机身尾部,红外信号的强度相对较大. 而在机翼-机身相连的部分,由于辐射的多次反射,其红外信号也相对较强.
|
图 7 等效辐射-汇聚法SDM模型成像面入射能流分布(ε=0.3) Figure 7 The radiative flux on imaging arrays of the SDM model by the equivalent radiation-concentrating method(ε=0.3) |
在光线数为104的条件下,同时计算了发射率为0.6和0.9时的红外热像. 图 8为不同表面发射率,(0,-1,0)方向、距离为1 km,SDM模型在像面竖直中间线上的入射能流,其中的相对值以横坐标原点的数值为基准计算. 从图 8中可以看出,目标的红外信号随其发射率的降低而减弱. 此外,在横轴两端附近,信号的强度近似与发射率成正比;而在机身-机翼等连接部位,随着发射率的降低,红外信号的相对强度显著增强.

|
图 8 等效辐射-汇聚法目标(0,-1,0)方位、距离1 000 m时图 6(a)成像面水平中线能流密度 Figure 8 The radiative flux on the horizontal middle cross section of the imaging arrays from the (0,-1,0) azimuth by the equivalent radiation-concentrating method |
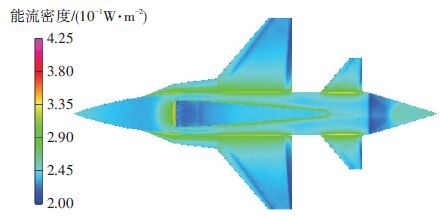
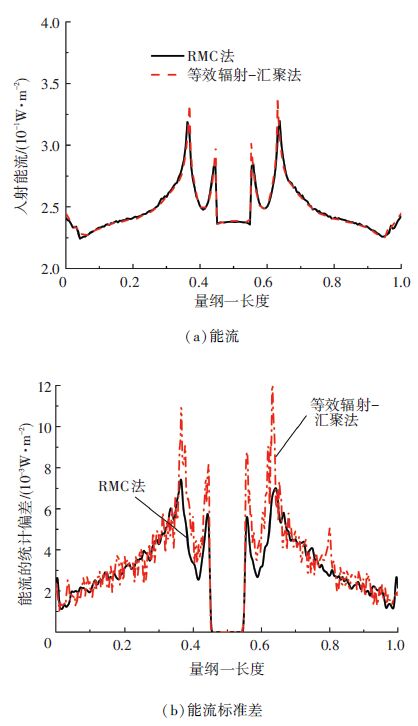
为进一步评价本文提出的方法,采用RMC[8]法计算了SDM模型在表面发射率为0.3时的红外热像,并将两种方法进行了对比. 计算中,探测阵列的像素为500×500,每个像素发射104根光线. 图 9为像面的入射辐射能流,图 10(a)为像面竖直中线上两种方法的入射能流的对比. 无论是图 7(a)和图 9间的定性还是图 10(a)中的定量对比都表明,本文提出的等效辐射-汇聚法的计算结果可信.
|
图 9 (0,-1,0) 方位RMC法SDM模型成像面入射能流密度分布 Figure 9 The radiative flux on imaging arrays of the SDM model from the (0,-1,0) azimuth by RMC method |
|
图 10 (0,-1,0)方位成像面水平中间线能流及其标准差对比 Figure 10 Comparisons between radiative fluxes and between their standard deviations from the (0,-1,0) azimuth by the RMC method and the equivalent radiation concentrating method |
现对等效辐射-汇聚法和RMC法的计算效率进行对比. 在表面发射率为0.3、单元(或像素)发射光线数为100的条件下,经过100次重复计算,得出了两种方法像面入射能流的统计标准差. 此计算条件下二者的计算时间不相同,为此,利用上述标准差与计算时间的平方根成反比这样的关系,以等效辐射-汇聚法为基准将RMC的标准差进行了换算.
图 10(b)为经过换算的在相同计算时间条件下,图 7(a)中像面竖直中线上的上述标准差的分布. 从图 10(b)中可以看出,二者的差别很小. 二者的标准差最大值分别为1.2 W·m-2左右. 由于标准差的数值与单元抽样光线数的平方根成反比,因此可以认为光线数为104根时的标准差在0.12 W·m-2左右,即光线数为104的计算结果可认为与抽样光线数无关. 由于相同计算时间条件下两种方法计算的能流的标准差相当,所以可以认为:对于如图 7(a)所示的单个探测方位,等效辐射-汇聚法与RMC方法的计算效率相当. 同时,对于如图 7所示多个探测方位,RMC法在每个探测方位的计算时间都与图 7(a)所示方位相当,总的计算时间将为图 7(a)所示方位的4倍左右,因为RMC法将等效辐射的形成及在光学系统中的汇聚成像进行一体化计算;而对于等效辐射-汇聚法,由于等效辐射或辐射传递因子的可复用性,总的计算时间接近于图 7(a)所示方位的1倍,因为在该法中,等效辐射的计算时间远大于其在红外光学系统中成像的计算时间.
4 结 论针对漫射表面目标,从其在光学系统中成像的物理过程出发,提出了其红外成像模拟计算的等效辐射-汇聚法. 通过算例的计算与对比验证了计算方法的准确性;同时,与反向蒙特卡洛方法相比,在多探测方位红外成像的模拟计算中,等效辐射-汇聚法由于其中目标的等效辐射(或辐射传递因子)具有独立性和可复用性,所以具有更高的计算效率.
本文的主要创新点归纳如下:
1) 考虑到目标等效辐射(或辐射传递因子)的相对独立性,将目标红外成像过程分解为目标表面辐射场的产生、空间传输与其红外系统中的汇聚成像两个阶段分别进行计算.
2) 基于等效辐射的各个部分之间(直接发射和反射)由于发射源的温度差异导致的大气衰减率的差异,通过蒙特卡罗法,将等效辐射场的产生与其大气传输耦合在一起进行模拟计算.
3) 目标到光学系统间的距离通常远大于目标尺寸,并且光学系统入瞳面上各点到目标的距离相差很小. 基于上述假设,忽略表面辐射在相互反射过程中的大气衰减,并利用目标点到入瞳面中心的距离采用逐线计算法计算单元直接辐射的衰减率.
4) 为减少蒙特卡罗方法中光线与单元求交的计算量,利用了八叉树区域分割方法对目标表面离散单元进行了分组.
5) 对于目标表面等效辐射在红外光学系统中汇聚成像的计算,利用光学成像变换关系确定了目标任意点的成像方位;根据成像系统中的光强传输变化得出了汇聚到成像点的红外辐照强度.
| [1] | BARANOWSKI L C, DOUGLAS M. Surface infrared signature computer program[C]//AIAA/ASME 3rd joint thermophysics, fluids, plasma and heat Transfer Conference. Louis: AIAA, 1982: 1-8. DOI: 10.2514/6.1982-914. |
| [2] |
杜胜华, 龚加明, 夏新林. 某飞行器红外辐射特性研究[J].
红外与激光工程, 2008, 37 (增刊) : 432-436.
DU Shenghua, GONG Jiaming, XIA Xinlin. Infrared characteristics of a spacecraft[J]. Infrared and laser engineering, 2008, 37 (增刊) : 432-436. |
| [3] |
单勇, 张靖周, 郭荣伟. 导弹蒙皮红外辐射特性的数值计算与分析[J].
航空动力学报, 2008, 23 (2) : 251-255.
SHAN Yong, ZHANG Jingzhou, GUO Rongwei. Numerical computation and analysis of the infrared radiation characteristic of missile scarfskin[J]. Journal of aerospace power, 2008, 23 (2) : 251-255. |
| [4] |
刘立, 孟卫华, 潘国庆. 超音速飞行环境中光学头罩热辐射建模与分析[J].
红外与激光工程, 2011, 40 (7) : 1193-1198.
LIU Li, MENG Weihua, PAN Guoqing. Modeling and analysis of infrared radiation from the dome flying at supersonic speed[J]. Infrared and laser engineering, 2011, 40 (7) : 1193-1198. |
| [5] | COIRO E. Global illumination technique for aircraft infrared signature calculations[J]. Journal of Aircraft, 2013, 50 (1) : 103-113. DOI: 10.2514/1.C031787 |
| [6] | SURZHIKOV S T. Hybrid Monte-Carlo/random model of molecular lines algorithm for signature prediction[C]//44th AIAA Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2006: 1-18. DOI:10.2514/6.2006-1187. |
| [7] | ROSS M, WERNER M, MAZUK S, et al. Infrared imagery of the space shuttle at hypersonic entry conditions[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2008:1-16. DOI:10.2514/6.2008-636. |
| [8] | SUN Haifeng, XIA Xinlin, SUN Chuang, et al. Spectral backward Monte Carlo method for surface infrared image simulation[C]//International Symposium on Optoelectronic Technology and Application: Infrared Technology and Applications. Beijing: SPIE, 2014: 9300L1-9300L9. DOI: 10.1117/12.2070699. |
| [9] |
周彦平, 卢春莲, 杨莉莉, 等. 空间目标可见光反射特性的研究[J].
哈尔滨工业大学学报, 2010, 42 (11) : 1717-1719.
ZHOU Yanping, LU Chunlian, YANG Lili, et al. Visible light reflection characteristics of space target[J]. Journal of Harbin Institute of Technology, 2010, 42 (11) : 1717-1719. |
| [10] |
王雁鸣, 董士奎, 谈和平, 等. 窄谱带模型数值研究高温喷流动态红外特性[J].
哈尔滨工业大学学报, 2009, 41 (11) : 1771-1774.
WANG Yanming, DONG Shikui, TAN Heping, et al. Numerical study on dynamic infrared properties of high temperature jet flow using narrow-band model[J]. Journal of Harbin Institute of Technology, 2009, 41 (11) : 1771-1774. |
| [11] | ROTHMAN L S, GORDON I E, BARBE A, et al. The HITRAN 2008 molecular spectroscopic database[J]. Journal of quantitive spectroscopy and radiative transfer, 2009, 110 (9/10) : 533-572. DOI: 10.1016/j.jqsrt.2009.02.013 |
| [12] |
谈和平, 夏新林, 刘林华, 等.
红外辐射与传输的数值计算: 计算辐射学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006 : 18 -19.
TAN Heping, XIA Xinlin, LIU Linhua, et al. Numerical simulation on Infrared Radiation and its Transfer:Computational Radiation[M]. Harbin: Harbin Institude of Technology Press, 2006 : 18 -19. |
| [13] | COULTER S M, MARQUART E J. Cross and cross-coupling derivative measurements on the standard dynamic at AEDC[C]//12th Aerodynamic Testing Conference. Williamsburg: AIAA,1982:202-214. DOI: 10.2514/6.1982-596. |
| [14] |
夏新林, 艾青, 任德鹏. 飞机蒙皮红外辐射的瞬态温度场分析[J].
红外与毫米波学报, 2007, 26 (3) : 174-177.
XIA Xinlin, AI Qing, REN Depeng. Analysis on the transient temperature fields for infrared radiation of aircraft skin[J]. J Infrared Millim Waves, 2007, 26 (3) : 174-177. DOI: 10.3321/j.issn:1001-9014.2007.03.004 |
| [15] |
刘林华, 董士奎, 余其铮, 等. 红外1~14μm波长间隔0.1μm 上大气平均透过率: (Ⅰ)二氧化碳的透过率[J].
哈尔滨工业大学学报, 1998, 30 (5) : 8-12.
LIU Linhua, DONG Shikui, YU Qizheng, et al. Atmospheric mean transmittance in wavelength interval 0 1 μ m from infrared 1 to 14 μm: (Ⅰ) transmittance of carbon dioxide[J]. Journal of Harbin Institute of Technology, 1998, 30 (5) : 8-12. |
| [16] |
梅飞, 江勇, 陈世国, 等. 一种气体吸收的逐线计算模型及其实验验证[J].
光学学报, 2012, 32 (3) : 21-27.
MEI Fei, JIANG Yong, CHEN Shiguo, et al. Experimental verification for line by line prediction model of gas absorption[J]. Acta Optica Sinica, 2012, 32 (3) : 21-27. |
 2017, Vol. 49
2017, Vol. 49


