CO2捕集主要有3种方法:燃烧后捕集、燃烧前捕集与富氧燃烧捕集[1]. 其中燃烧后捕集方法指从化石燃料燃烧后产生的混合烟气中捕获CO2气体. 燃烧后二氧化碳捕获技术具体又分为以下几种:溶剂吸收法、物理吸附法、低温蒸馏法与膜分离法[2]. 燃煤电厂烟气中的CO2含量较低,适合的CO2捕捉方法主要为化学溶剂吸收法与膜分离方法. 目前最主要的捕获方法是化学溶剂吸收法,也是目前工业上最常用的方法[3].
常用的化学吸收剂有有机胺溶液、氨水、强碱溶液等[4]. 其中乙醇胺(MEA)吸收酸性气体速率快,吸收能力强,价格低廉,广泛应用于工业二氧化碳吸收过程[5-6].
随着计算机技术的发展,利用计算流体动力学(CFD)对CO2碳捕捉过程进行模拟成为新的研究方向[7-9]. 将CFD理论与实际工程相结合,实现CO2捕集过程的模拟,对改进和完善当前的吸收反应设备,实现CO2高效率吸收起到重要的指导作用. 目前的CFD模型仅限于在填料单元上模拟气液两相流动情况,很少涉及气液两相间的化学反应.
本文运用溶剂吸收法,加入化学反应与质量传递过程,利用Fluent模拟填料单元内MEA溶液吸收CO2的过程. 塔内采用Montz-pak B1 250.45型规整填料,通过建立三维周期单元模型模拟中尺度下填料层内乙醇胺吸收CO2的化学反应过程,近似得到在该填料单元内CO2的吸收率. 随后改变吸收过程的操作条件(如改变入口气液流量比、CO2入口质量分数、乙醇胺摩尔分数、压强等),得到不同操作条件下CO2吸收率,分析碳捕集过程的影响因素.
1 CFD模拟过程 1.1 数学模型 1.1.1 基本方程设气相为理想气体,液相为不可压缩流体,瞬态流动,且流动过程为恒温,则质量守恒方程为
| $\frac{{\partial ({\alpha _k}{\rho _k})}}{{\partial t}} + \nabla \cdot({\alpha _k}{\rho _k}{u_k}) = {S_k},$ |
动量守恒方程为
| $\begin{gathered} \frac{{\partial ({\alpha _k}{\rho _k}{u_k})}}{{\partial t}} + \nabla \cdot({\alpha _k}{\rho _k}{u_k}{u_k}) = - {\alpha _k}\nabla p + \hfill \\ {\nabla ^2}\left( {{\alpha _k}{\mu _k}{u_k}} \right) + {\alpha _k}{\rho _k}{g_k} + {F_k}, \hfill \\ \end{gathered} $ |
能量守恒方程为
| $\begin{gathered} \frac{{\partial ({\alpha _k}{\rho _k}{h_k})}}{{\partial t}} + \nabla \cdot({\alpha _k}{\rho _k}{u_k}{h_k}) = {\alpha _k}\frac{{\partial p}}{{\partial t}} + \hfill \\ \nabla \cdot\left( {{\lambda _k}\nabla {T_k}} \right) + {Q_k} + {S_{e,k}}. \hfill \\ \end{gathered} $ |
式中:uk为速度向量,ρk为第k相的密度,Sk为质量源项,p为静压,μk为动力黏度,gk为重力体积力,Fk为相间相互作用力,hk为第k种物质的比焓,λk为热导系数,Qk为相间热传导强度,Se,k为化学反应中焓源项.
1.1.2 湍流模型采用标准k-ε模型,湍动能k与耗散率ε是两个基本未知量.
| $\begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon , \hfill \\ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \rho \varepsilon {u_i}}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \hfill \\ \frac{{{C_{1\varepsilon }}\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}. \hfill \\ \end{gathered} $ |
式中:
| $\begin{gathered} {C_{1\varepsilon }} = 1.44,{\text{ }}{C_{2\varepsilon }} = 1.92, \hfill \\ {\sigma _k} = 1.00,{\text{ }}{\sigma _\varepsilon } = 1.30. \hfill \\ \end{gathered} $ |
第k (k=1,2)相流体的化学组分守恒方程采用以下通用形式:
| $\frac{\partial }{{\partial t}}(\rho {Y_i}) + \nabla \cdot(\rho \vec v{Y_i}) = - \nabla {\vec J_i} + {R_i} + {S_i}.$ |
其中Yi为第i种物质的质量分数,Ri为化学反应的净产生速率,Si为离散相或者自定义源项产生的速率. 在系统中出现N种物质时,各种物质质量分数之和为1.
湍流质量扩散系数为
| ${{\vec J}_i} = - (\rho {D_{i,m}} + \frac{{{\mu _t}}}{{S{c_t}}})\nabla {Y_i},$ |
式中Di,m是第i种物质的扩散系数,Sct是湍流施密特数,默认值为0.7.
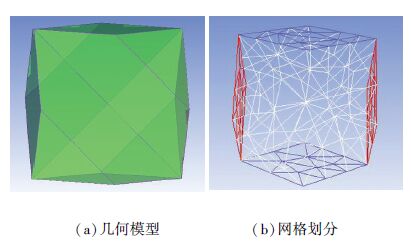
1.2 物理模型采用Montz-pak B1 250.45型规整填料,填料板倾角为45°,几何参数见表 1. 本文从填料层中提取出周期性填料单元,在ICEM CFD中建立三维模型,如图 1所示,由于填料单元内部弯曲折角较多,故采用非结构化方法进行网格划分. 网格划分最大尺寸为8 mm,整个模型生成300多个网格单元.
| 表 1 Montz-pak B1-250.45填料几何参数 Table 1 Geometric parameters of Montz-pak B1-250.45 |
|
图 1 填料周期单元模型 Figure 1 Periodic unit cell model of structured packing |
采用通用有限速率模型来模拟乙醇胺与CO2的吸收反应. 在Fluent中设置通用有限速率模型模拟化学反应时,首先定义反应物和生成物各组分及其相关物性;其次定义化学反应;最后给出相关化学反应的动力学数据.
MEA吸收CO2的反应过程比较复杂,模拟过程中将反应简化,假定为二级不可逆反应,总的反应方程式为
| $C{O_2} + 2MEA\xrightarrow{{{k_2}}}MEA{H^ + } + MEACO{O^ - }.$ | (1) |
CO2在MEA溶液中的扩散系数与溶解度可采用文献[10]数据,分别为8.39×10-10 m2/s,0.808 mol/mol;乙醇胺的扩散系数为1.1×10-10 m2/s[11]. 由于Fluent数据库中没有MEA以及相关产物的数据,通过Aspen数据库得到它们的基本物理性质数据见表 2.
| 表 2 主要物质基本物性 Table 2 The physical property of main materials |
式(1)中正向反应速率常数k2由阿伦尼乌斯公式计算:
| ${k_2} = A{e^{ - {E_a}/RT}}.$ |
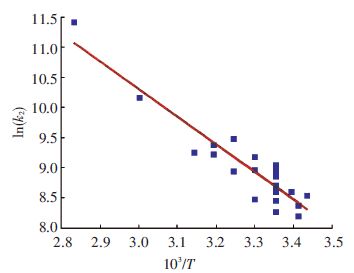
其中A是指数前因子,Ea是反应活化能,R是理想气体常数. 本文根据Aboudheir等[12]总结前人的试验数据,对其进行半对数拟合,拟合结果如图 2所示.
|
图 2 反应速率与温度的半对数拟合 Figure 2 Semi-log fitting of reacting rate vs. temperature |
图 2中,以103/T为横坐标,ln(k2)为纵坐标,ln A为图中的截距,-(Ea/R)×10-3为斜率,可以依此求出A与Ea,分别为2.678×1010与3.798 2×104.
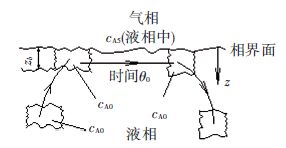
1.4 质量传递模型在实际传质过程中,气液两相在高度湍动状态下互相接触,此时不存在稳定的相界面. Higbit[13]在建立的溶质渗透模型中指出:在填料塔中,气液两相接触时间很短,故应根据非稳态扩散模型来处理[14]. 图 3为溶质渗透模型的示意图. 本文采用溶质渗透模型,编写用户自定义函数(UDF),导入至Fluent中进行编译计算.
|
图 3 溶质渗透模型示意 Figure 3 The diagram of penetration theory |
溶质在流体单元内进行的是一维非稳态扩散过程. CO2的吸收模拟过程,在CO2从气相扩散至气液界面时伴有二级化学反应,CO2与MEA的生成速率分别为
| $\begin{gathered} {r_{C{O_2}}} = - {k_2}{c_{C{O_2}}}{c_{MEA}}, \hfill \\ {r_{MEA}} = - 2{k_2}{c_{C{O_2}}}{c_{MEA}}; \hfill \\ \end{gathered} $ |
CO2的传质微分方程可表示为
| ${D^{Solution}}_{C{O_2}}\frac{{{\partial ^2}{c_{C{O_2}}}}}{{\partial {y^2}}} = \frac{{\partial {c_{C{O_2}}}}}{{\partial t}} - {r_{C{O_2}}}.$ |
由于反应速率很大,是瞬间反应,且假设二者的扩散系数相等,根据溶质渗透理论得到传质系数[15]:
| ${k_{L,{\text{ }}C{O_2}}} = \left( {1 + \frac{{{c_{MEA}}}}{{2{c_{C{O_2},{\text{ }}i}}}}} \right){\left( {\frac{{4{D_{CO}}_2}}{{\pi {\theta _c}}}} \right)^{\frac{1}{2}}}.$ |
将传质系数代入质量源项Sm,
| ${S_m} = M{k_{L,CO}}_2A{C_L}({c_{CO}}_2{,_i} - {c_{CO}}_2,0)/V.$ |
式中M为CO2的摩尔质量,A为单元接触面积,CL为溶液总的摩尔浓度,cCO2,i与cCO2,0分别表示二氧化碳在界面与液相主体的浓度,V为单元体积.
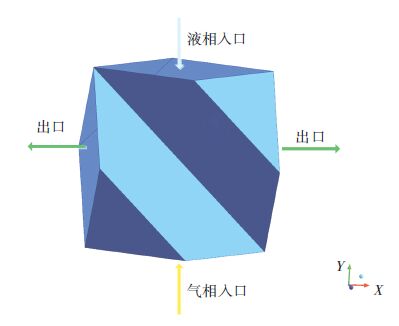
1.5 边界条件边界条件参考华能碳捕集试验研究文献[6]. 边界条件具体设置如图 4所示.
|
图 4 周期单元边界条件 Figure 4 Boundary conditions of REU |
将气相设为主相,液相设为第二相. 基本压力设为1 kPa. 由于液相的加入,考虑重力的影响,且重力大小为9.8,方向为y轴负方向.
1) 气相入口,采用速度入口,方向垂直进口面. 气体入口流量为2 250 m3/h,塔径为1.2 m,转化成气体入口速度为0.552 6 m/s. 进口烟气简化为CO2与N2的混合气体,其中CO2的质量分数为14%.
2) 液相入口,采用速度入口,方向垂直于进口面. 入口流量为3×104 L/h,转化成液体入口速度为0.007 37 m/s. 进口组分为MEA与水,其中MEA的摩尔分数为5%,文中MEA浓度均由摩尔分数来表示.
3) 出口设置,设置两边出口均为压力出口,大小设为1 kPa.
4) 壁面设置,设置壁面为无滑移壁面,忽略流体与填料之间的相互作用.
5) 化学反应,采用组分输运模型和通用有限速率模型,操作温度为300 K,操作压强为1 kPa.
6) 湍流模型,采用标准k-ε模型.
7) 其他设置,压力速度耦合采用简单算法,离散化方法中压力项采用标准算法,动量、湍动能、耗散率离散格式均采用一阶迎风标准,松弛因子及残差均为默认值,设置单位步长为0.001 s,模拟1.5 s的反应过程.
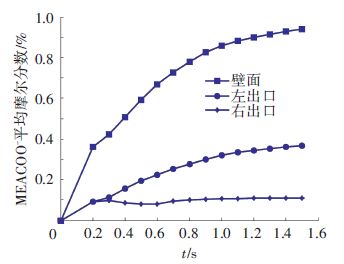
2 乙醇胺吸收二氧化碳模拟结果 2.1 CO2吸收率CO2气相传至液相,然后与液相中的MEA发生反应,生成MEACOO-与MEAH+,由总反应化学方程式可知,1摩尔CO2对应生成1摩尔MEACOO-,MEACOO-的量可以代表CO2吸收的情况. 不同时刻MEACOO-在壁面与出口的平均摩尔分数如图 5所示.
|
图 5 MEACOO-在壁面与出口的平均摩尔分数 Figure 5 Mean mole fraction of MEACOO- at wall and outlet |
随着流体的流动与反应的进行,MEACOO-浓度不断增加,随后趋于稳定. 初始时刻,气液两相接触发生化学反应,生成产物MEACOO-,在0 ~ 1.0 s的时间内MEACOO-在填料表面与出口面均逐渐增加,此时间段内大量生成MEACOO-,在1.0 s以后,增长速率减缓,开始趋于稳定,此时填料内部的化学反应也达到稳定状态.
单元内生成的MEACOO-主要集中在填料壁面,两个出口面的平均摩尔分数少于壁面,表明每一时刻会有产物移出填料单元,且浓度占总体的1/5左右,不可忽略. 故CO2的吸收率定义为壁面的MEACOO-与两个出口面平均的MEACOO-浓度之和.
不同气速下填料单元内液相分布如图 6所示,液相体积分数代表液相分布,气体流速影响液相分布,气体流速越慢,则液体受气体的影响越小,流动状态波动也越小,从而在填料表面流动的面积越大.

|
图 6 不同气速下填料单元内液相分布 Figure 6 Liquid phase distribution versus gas velocity |
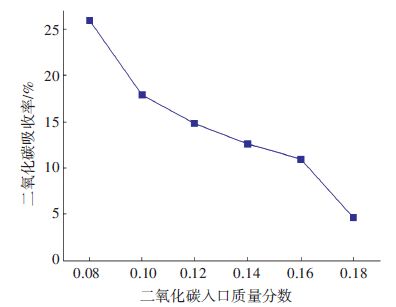
为分析烟气CO2浓度对吸收效率的影响,设定液体流量3×104 L/h,烟气流量为2 250 m3/h,MEA摩尔分数为0.05,压强与温度分别为1 kPa与300 K,仅改变烟气CO2的质量分数,依次取烟气CO2质量分数0.08、0.10、0.12、0.14、0.16和0.18. 模拟结果见图 7.
|
图 7 不同CO2质量分数下的烟气CO2吸收率 Figure 7 CO2 absorptivity versus CO2 mass fraction |
由图 7可知,CO2吸收率随入口质量分数的升高而降低. 将模拟结果与试验结果[16]进行了对比,试验中设定反应温度为303 K,MEA摩尔分数为26%,以4 L/min的流量向反应器内通入CO2质量分数分别为9%、12%、15%和18%的烟气. 模拟结果趋势与实验结果一致.
CO2质量浓度增大,则乙醇胺与二氧化碳的摩尔比值减小,从化学平衡角度来看,正向反应推动力减小,不利于CO2吸收. 烟气中CO2浓度升高,气相分压提高,进入液相主体中的CO2的量增大,但抵消其对初始浓度的增大作用,所以随着烟气浓度的升高,吸收效率反而降低.
2.2.2 乙醇胺摩尔分数为分析MEA摩尔分数对二氧化碳吸收效率的影响,仅改变MEA摩尔分数,其他边界条件不变,设定流量3×104 L/h,烟气流量2 250 m3/h为液体75倍,烟气CO2质量分数为14%,压强与温度分别为1 kPa与300 K,乙醇胺摩尔分数依此取0.02、0.05、0.10、0.15、0.20和0.30.
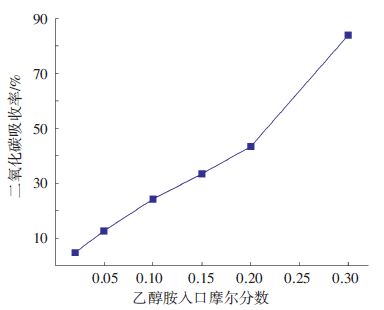
模拟结果如图 8所示,CO2吸收率随MEA摩尔分数的增加而明显上升.
|
图 8 不同乙醇胺摩尔分数下CO2吸收率 Figure 8 CO2 absorptivity versus MEA mole fraction |
文献[16]试验中设定反应温度为303 K,将CO2质量分数为15%的模拟烟气以4 L/min的流量通入MEA摩尔分数分别为8%、17%、26%与35%的吸收溶液中,模拟结果与试验结果趋势相同. 随MEA浓度的增加,CO2吸收速率升高. 因为MEA摩尔浓度的增加,增大了其与CO2的摩尔比,使得CO2从气相传至液相马上与之反应,气液界面与液相主体的传质推动率增强,从而使得CO2吸收效率升高.
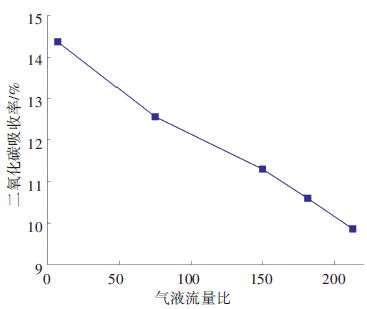
2.2.3 气液流量比为分析气液流量比对CO2吸收效率的影响,设定液体流量3×104 L/h,烟气CO2质量分数为14%,MEA溶液摩尔分数为5%,操作温度300 K与压强1 kPa,仅改变入口烟气流量,依此选取烟气流量为液体流量的7.50、75.00、150.00、181.25与212.50倍. 模拟结果如图 9所示,CO2吸收率随气液流量比的增大而降低. 将模拟结果与文献[16]的试验结果进行对比,试验采用通气式搅拌釜作为主体反应器,温度为303 K,吸收溶液摩尔分数为26%,模拟烟气中CO2质量分数为12%时,随烟气流量的增加,CO2脱除率降低,与本文模拟结果趋势一致.
气液流量比增大意味着气液两相在填料单元内停留的时间减少,且气体会将吸收剂带出填料单元,所以CO2吸收率随气液流量比的增大而降低. 气液流量比还关系到填料层的充分浸润,气液流量比过高,会导致液体流不下来,进而导致液泛.
|
图 9 不同气液流量比下CO2吸收率 Figure 9 CO2 absorptivity versus ratio of gas-liquid flow |
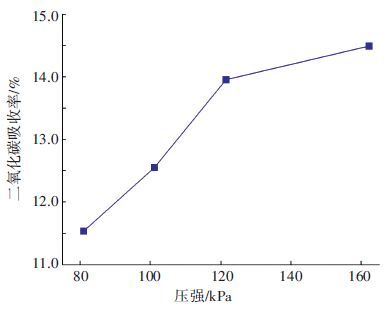
为分析压强对CO2吸收效率的影响,仅改变压强,其他边界条件不变,烟气流量为2 250 m3/h、液体流量3×104 L/h、烟气CO2质量分数为14%、乙醇胺摩尔分数为5%、操作温度300 K,结果如图 10所示.
|
图 10 不同环境压强下二氧化碳吸收率 Figure 10 CO2 absorptivity versus pressure |
CO2吸收量随压强增大而增多,原因在于压强的增大,使化学平衡朝正向移动,反应推动力增大,化学反应更加充分,吸收率也就升高了. 在实际操作中,发电厂烟气量大,会带来很多的能源消耗,并且增压需要耐压设备,费用较大,极不经济.
2.2.5 影响因素排序为定量分析各个影响因素及其交互作用对CO2吸收影响的大小,分别用A、B、C、D代表烟气CO2质量分数、MEA摩尔分数、气液流量比与环境压强,两两因素的交互作用分别用A*B、A*C、A*D、B*C、B*D、C*D表示,交互作用的吸收效率由对应的影响因素的吸收效率乘积得到. 选取每个因素的高低两个水平值,并进行组合得到24=16种模拟方案. 16种模拟方案参数设置及模拟得到对应的CO2吸收率,如表 3所示.
| 表 3 模拟方案与结果 Table 3 Simulation results |
对每个因素影响大小进行极差分析并进行排列,如图 11所示.

|
图 11 不同因素影响大小排列图 Figure 11 Pareto of different influence factors |
影响因素B,即MEA质量分数对吸收影响最大(占比38%),其次依次是MEA摩尔分数与CO2质量分数交互作用、CO2质量分数、气液流量比、MEA摩尔分数与气液流量比交互作用、气液流量比与压强交互作用. 以上影响因素及其交互作用对吸收的影响累积达到96%,剩余的4个因素或交互作用对吸收影响忽略不计.
2.3 最优参数实际应用中,在满足工艺要求的前提下,还需综合考虑CO2的吸收效率、胺降解、运营成本等问题. 本文中,当烟气流量为2 250 m3/h,CO2质量分数为14%时,选取MEA溶液为烟气流量的1/10,即225 m3/h,MEA摩尔分数选取20%~30%,温度为300 K,压强为常压,才使模拟得到的CO2吸收效率是最高的.
3 结 论1) 模拟了中尺度下吸收塔规整填料单元内乙醇胺吸收CO2的传质与吸收过程,并通过填料表面MEACOO-在壁面与出口面的平均摩尔分数值近似计算得到CO2的吸收率. MEA吸收CO2的过程,属于带化学反应的气液两相流动过程,气液两相接触时间越长,反应越充分,则生成的MEACOO-越多.
2) 模拟分析了不同操作条件下规整填料单元内MEA吸收CO2的化学反应,并得到不同操作条件对CO2吸收率的影响.
3) 对因素影响大小进行定量分析,MEA摩尔分数对吸收效率影响最突出,其次依次是CO2入口浓度、气液入口流量比、压强. 在实际碳捕集过程中,电厂燃烧烟气中CO2初始浓度是确定的,需要根据操作条件确定合理的气液流量、乙醇胺浓度,从而保证CO2最大脱除率.
本文模拟是在局部填料单元模型上进行的,未考虑吸收塔塔壁与材质对吸收过程的影响. 该方法是利用Fluent软件对碳捕集过程模拟的一种尝试. 在该方法的基础上,将来在计算机性能允许的条件下,利用CFD可以实现在规整填料塔整体模型上的碳捕集过程模拟.
| [1] | MACDOWELL N, FLORIN N, BUCHARD A, et al. An overview of CO2 capture technologies[J]. Energy & Environmental Science, 2010, 3 (11) : 1645-1669. DOI: 10.1039/c004106h |
| [2] | WHITE C M, STRAZISAR B R, GRANTIE E J, et al. Separation and capture of CO2 from stationary sources and sequestration in geological formations coalbeds and deep saline aquifers[J]. Journal of the Air & Waste Management Association, 2003, 53 (6) : 645-715. DOI: 10.1080/10473289.2003.10466206 |
| [3] |
黄斌, 许世森, 郜时旺, 等. 华能北京热电厂CO2捕集工业试验研究[J].
中国机电工程学报, 2009, 29 (17) : 14-20.
HUANG Bin, XU Shisen S, GAO Shiwang, et al. Industrial test of CO2 capture in Huaneng Beijing coal-fired power station[J]. Proceedings of the CSEE, 2009, 29 (17) : 14-20. DOI: 10.3321/j.issn:0258-8013.2009.17.003 |
| [4] | PENG Y, ZHAO B, LI L. Advance in post combustion CO2 capture with alkaline solution: a brief review[J]. Energy Procedia, 2012, 14 (1) : 1515-1522. DOI: 10.1016/j.egypro.2011.12.1126 |
| [5] | KITTEL J, IDEM R, GELOWITZ, et al. Corrosion in MEA units for CO2 capture: pilot plant studies[J]. Energy Procedia, 2009, 1 (1) : 791-797. DOI: 10.1016/j.egypro.2009.01.105 |
| [6] | LEPAUMIER H, DA SILVA E F, EINBU A, et al. Comparison of MEA degradation in pilot-scale with lab-scale experiments[J]. Energy Procedia, 2011, 4 (1) : 1652-1659. DOI: 10.1016/j.egypro.2011.02.037 |
| [7] | ASENDRYCH D, NIEGODAJEW P, DROBNIAK S. CFD modeling of CO2 capture in a packed bed by chemical absorption[J]. Chemical and Process Engineering, 2013, 34 (2) : 269-282. DOI: 10.2478/cpe-2013-0022 |
| [8] |
徐斌. 面向建材应用的二氧化碳捕获过程CFD模拟[D]. 哈尔滨: 哈尔滨工业大学, 2014.
XU Bin. CFD simulation of carbon dioxide capture reactors for architectural materials application[D]. Harbin: Harbin institute of technology, 2014. |
| [9] |
代成娜, 项银, 雷志刚. 规整填料塔中离子液体吸收CO2的传质与流体力学性能[J].
化工学报, 2015, 66 (8) : 2953-2961.
DAI Chengna, XIANG Yin, LEI Zhigang G. Mass transfer and hydraulic performance of CO2 absorption by ionic liquids over structured packings[J]. Journal of Chemical Industry and Engineering, 2015, 66 (8) : 2953-2961. DOI: 10.11949/j.issn.0438-1157.20150753 |
| [10] | VERSTEE G F, VANSWAAIJ W P M. Solubility and diffusivity of acid gases (CO2, N2O) in aqueous alkanolamine solution[J]. Journal of Chemical & Engineering Data, 1988, 33 (1) : 29-34. DOI: 10.1021/je00051a011 |
| [11] | DANCKWERT L K, SHARMA M M. The absorption of carbon dioxide into solutions of alkalis and amines[J]. Chemical Engineering, 1966, 44 : 244-280. |
| [12] | TONTIWACHWUTHIKUL P, ABOUDHEIR A, IDEM R, et al. Kinetics of the reactive absorption of carbon dioxide in high CO2-loaded, concentrated aqueous monoethanolamine solutions[J]. Chemical Engineering Science, 2003, 58 (23) : 5195-5210. DOI: 10.1016/j.ces.2003.08.014 |
| [13] | HIGBIE R. The rate of absorption of a pure gas into a still liquid during shortperiod of exposure[J]. Transactions of the American Institute of Chemical Engineers, 1935, 1 (1) : 365-389. |
| [14] |
贾绍义, 柴诚敬.
化工传质与分离过程[M]. 北京: 化学工业出版社, 2007 : 43 -46.
JIA Shaoyi, CHAI Chengjing. Chemical mass transfer and separation process[M]. Beijing: Chemical Industry Press, 2007 : 43 -46. |
| [15] |
曾作祥.
传递过程原理[M]. 上海: 华东理工大学出版社, 2013 : 300 -302.
ZENG Zuoxiang. Transfer process principle[M]. Shanghai: East China University of Science and Technology press, 2013 : 300 -302. |
| [16] |
司南. 乙醇胺(MEA)溶液吸收CO2 的试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 27-32.
SI Nan. Experimental study on absorption of CO2 in aqueous monoethenolamine (MEA) solution[D]. Harbin: Harbin institute of technology,2009: 27-32. |
 2017, Vol. 49
2017, Vol. 49


